logo资料库

PCA的数学原理.pdf

发布时间：2022-06-20 发布人：admin 分类：说明书 资料大小：0.63M 资料格式：pdf 举报 版权申诉
第1页 / 共15页
第2页 / 共15页
第3页 / 共15页
第4页 / 共15页
第5页 / 共15页
第6页 / 共15页
第7页 / 共15页
第8页 / 共15页
资料共15页，剩余部分请下载后查看
    2019/1/9 CodingLabs keep coding, keep foolish CodingLabs - PCA的数学原理 首页 | 标签 | 关于我 | +订阅 | 微博 PCA的数学原理 作者 张洋 | 发布于 2013-06-22 机器学习 线性代数 PCA PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数 据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降 维。网上关于PCA的文章有很多，但是大多数只描述了PCA的分析过程，而没有讲述其中的原 理。这篇文章的目的是介绍PCA的基本数学原理，帮助读者了解PCA的工作机制是什么。 当然我并不打算把文章写成纯数学文章，而是希望用直观和易懂的方式叙述PCA的数学原理，所 以整个文章不会引入严格的数学推导。希望读者在看完这篇文章后能更好的明白PCA的工作原 理。 数据的向量表示及降维问题 一般情况下，在数据挖掘和机器学习中，数据被表示为向量。例如某个淘宝店2012年全年的流量 及交易情况可以看成一组记录的集合，其中每一天的数据是一条记录，格式如下： (日期, 浏览量, 访客数, 下单数, 成交数, 成交金额) 其中“日期”是一个记录标志而非度量值，而数据挖掘关心的大多是度量值，因此如果我们忽略日 期这个字段后，我们得到一组记录，每条记录可以被表示为一个五维向量，其中一条看起来大约 是这个样子： 注意这里我用了转置，因为习惯上使用列向量表示一条记录（后面会看到原因），本文后面也会 遵循这个准则。不过为了方便有时我会省略转置符号，但我们说到向量默认都是指列向量。 我们当然可以对这一组五维向量进行分析和挖掘，不过我们知道，很多机器学习算法的复杂度和 数据的维数有着密切关系，甚至与维数呈指数级关联。当然，这里区区五维的数据，也许还无所 谓，但是实际机器学习中处理成千上万甚至几十万维的情况也并不罕见，在这种情况下，机器学 习的资源消耗是不可接受的，因此我们必须对数据进行降维。 降维当然意味着信息的丢失，不过鉴于实际数据本身常常存在的相关性，我们可以想办法在降维 的同时将信息的损失尽量降低。 http://blog.codinglabs.org/articles/pca-tutorial.html 1/15 ( 5 0 0 , 2 4 0 , 2 5 , 1 3 , 2 3 1 2 . 1 5 ) T
    2019/1/9 CodingLabs - PCA的数学原理 举个例子，假如某学籍数据有两列M和F，其中M列的取值是如何此学生为男性取值1，为女性取 值0；而F列是学生为女性取值1，男性取值0。此时如果我们统计全部学籍数据，会发现对于任何 一条记录来说，当M为1时F必定为0，反之当M为0时F必定为1。在这种情况下，我们将M或F去 掉实际上没有任何信息的损失，因为只要保留一列就可以完全还原另一列。 当然上面是一个极端的情况，在现实中也许不会出现，不过类似的情况还是很常见的。例如上面 淘宝店铺的数据，从经验我们可以知道，“浏览量”和“访客数”往往具有较强的相关关系，而“下单 数”和“成交数”也具有较强的相关关系。这里我们非正式的使用“相关关系”这个词，可以直观理解 为“当某一天这个店铺的浏览量较高（或较低）时，我们应该很大程度上认为这天的访客数也较高 （或较低）”。后面的章节中我们会给出相关性的严格数学定义。 这种情况表明，如果我们删除浏览量或访客数其中一个指标，我们应该期待并不会丢失太多信 息。因此我们可以删除一个，以降低机器学习算法的复杂度。 上面给出的是降维的朴素思想描述，可以有助于直观理解降维的动机和可行性，但并不具有操作 指导意义。例如，我们到底删除哪一列损失的信息才最小？亦或根本不是单纯删除几列，而是通 过某些变换将原始数据变为更少的列但又使得丢失的信息最小？到底如何度量丢失信息的多少？ 如何根据原始数据决定具体的降维操作步骤？ 要回答上面的问题，就要对降维问题进行数学化和形式化的讨论。而PCA是一种具有严格数学基 础并且已被广泛采用的降维方法。下面我不会直接描述PCA，而是通过逐步分析问题，让我们一 起重新“发明”一遍PCA。 向量的表示及基变换 既然我们面对的数据被抽象为一组向量，那么下面有必要研究一些向量的数学性质。而这些数学 性质将成为后续导出PCA的理论基础。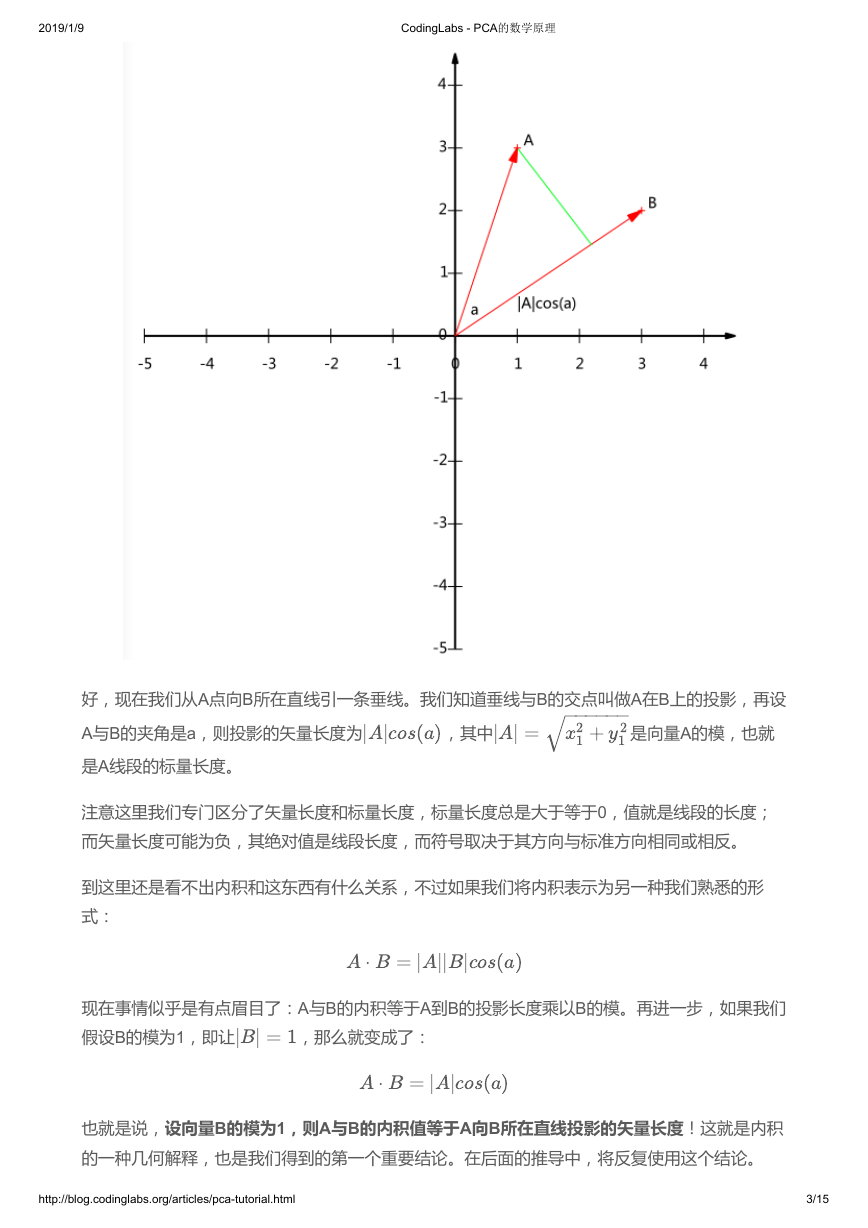 内积与投影 下面先来看一个高中就学过的向量运算：内积。两个维数相同的向量的内积被定义为： 内积运算将两个向量映射为一个实数。其计算方式非常容易理解，但是其意义并不明显。下面我 们分析内积的几何意义。假设A和B是两个n维向量，我们知道n维向量可以等价表示为n维空间中 ， 的一条从原点发射的有向线段，为了简单起见我们假设A和B均为二维向量，则 。则在二维平面上A和B可以用两条发自原点的有向线段表示，见下图： http://blog.codinglabs.org/articles/pca-tutorial.html 2/15 ( , , ⋯ , ⋅ ( , , ⋯ , = + + ⋯ + a 1 a 2 a n ) T b 1 b 2 b n ) T a 1 b 1 a 2 b 2 a n b n A = ( , ) x 1 y 1 B = ( , ) x 2 y 2
    2019/1/9 CodingLabs - PCA的数学原理 好，现在我们从A点向B所在直线引一条垂线。我们知道垂线与B的交点叫做A在B上的投影，再设 A与B的夹角是a，则投影的矢量长度为 是A线段的标量长度。 ，其中 是向量A的模，也就 注意这里我们专门区分了矢量长度和标量长度，标量长度总是大于等于0，值就是线段的长度； 而矢量长度可能为负，其绝对值是线段长度，而符号取决于其方向与标准方向相同或相反。 到这里还是看不出内积和这东西有什么关系，不过如果我们将内积表示为另一种我们熟悉的形 式： 现在事情似乎是有点眉目了：A与B的内积等于A到B的投影长度乘以B的模。再进一步，如果我们 假设B的模为1，即让 ，那么就变成了： 也就是说，设向量B的模为1，则A与B的内积值等于A向B所在直线投影的矢量长度！这就是内积 的一种几何解释，也是我们得到的第一个重要结论。在后面的推导中，将反复使用这个结论。 http://blog.codinglabs.org/articles/pca-tutorial.html 3/15 | A | c o s ( a ) | A | = + x 2 1 y 2 1 − − − − − − √ A ⋅ B = | A | | B | c o s ( a ) | B | = 1 A ⋅ B = | A | c o s ( a )
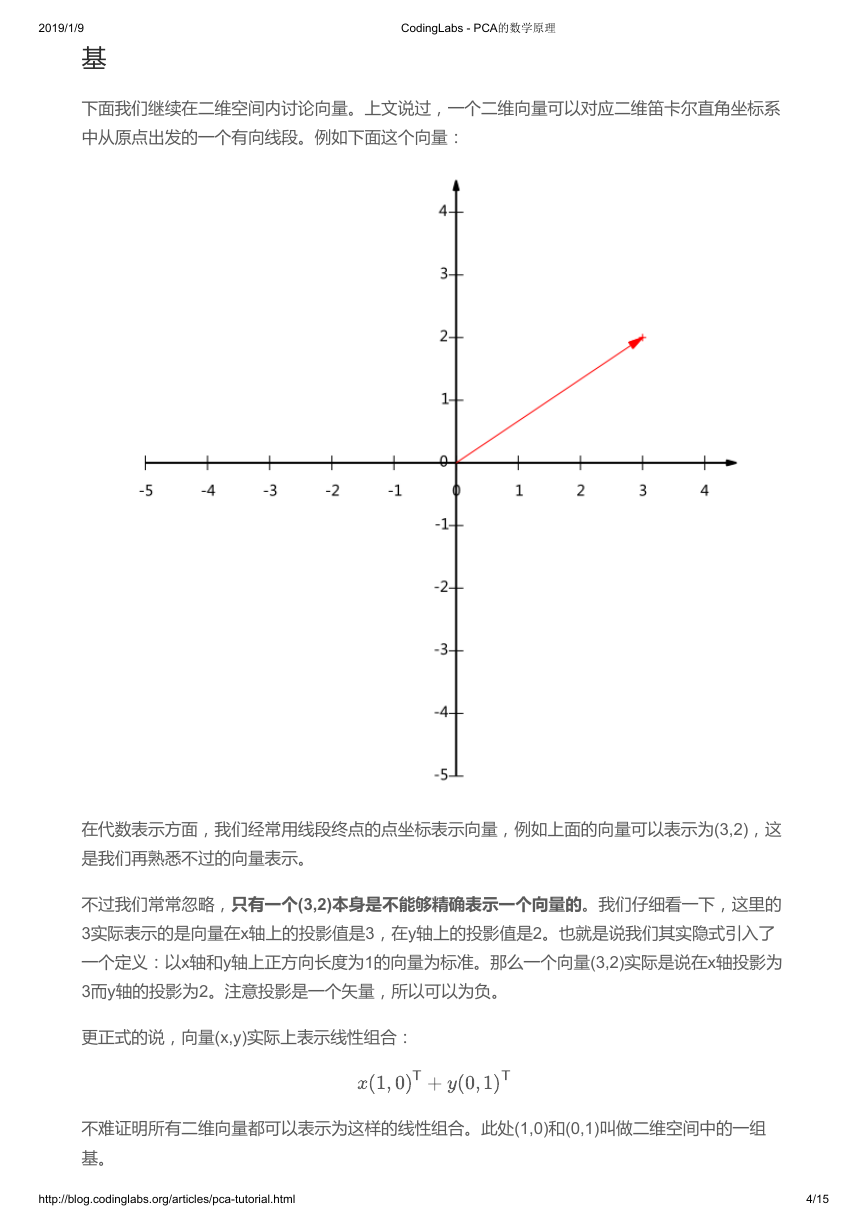
    2019/1/9 基 CodingLabs - PCA的数学原理 下面我们继续在二维空间内讨论向量。上文说过，一个二维向量可以对应二维笛卡尔直角坐标系 中从原点出发的一个有向线段。例如下面这个向量： 在代数表示方面，我们经常用线段终点的点坐标表示向量，例如上面的向量可以表示为(3,2)，这 是我们再熟悉不过的向量表示。 不过我们常常忽略，只有一个(3,2)本身是不能够精确表示一个向量的。我们仔细看一下，这里的 3实际表示的是向量在x轴上的投影值是3，在y轴上的投影值是2。也就是说我们其实隐式引入了 一个定义：以x轴和y轴上正方向长度为1的向量为标准。那么一个向量(3,2)实际是说在x轴投影为 3而y轴的投影为2。注意投影是一个矢量，所以可以为负。 更正式的说，向量(x,y)实际上表示线性组合： 不难证明所有二维向量都可以表示为这样的线性组合。此处(1,0)和(0,1)叫做二维空间中的一组 基。 http://blog.codinglabs.org/articles/pca-tutorial.html 4/15 x ( 1 , 0 + y ( 0 , 1 ) T ) T
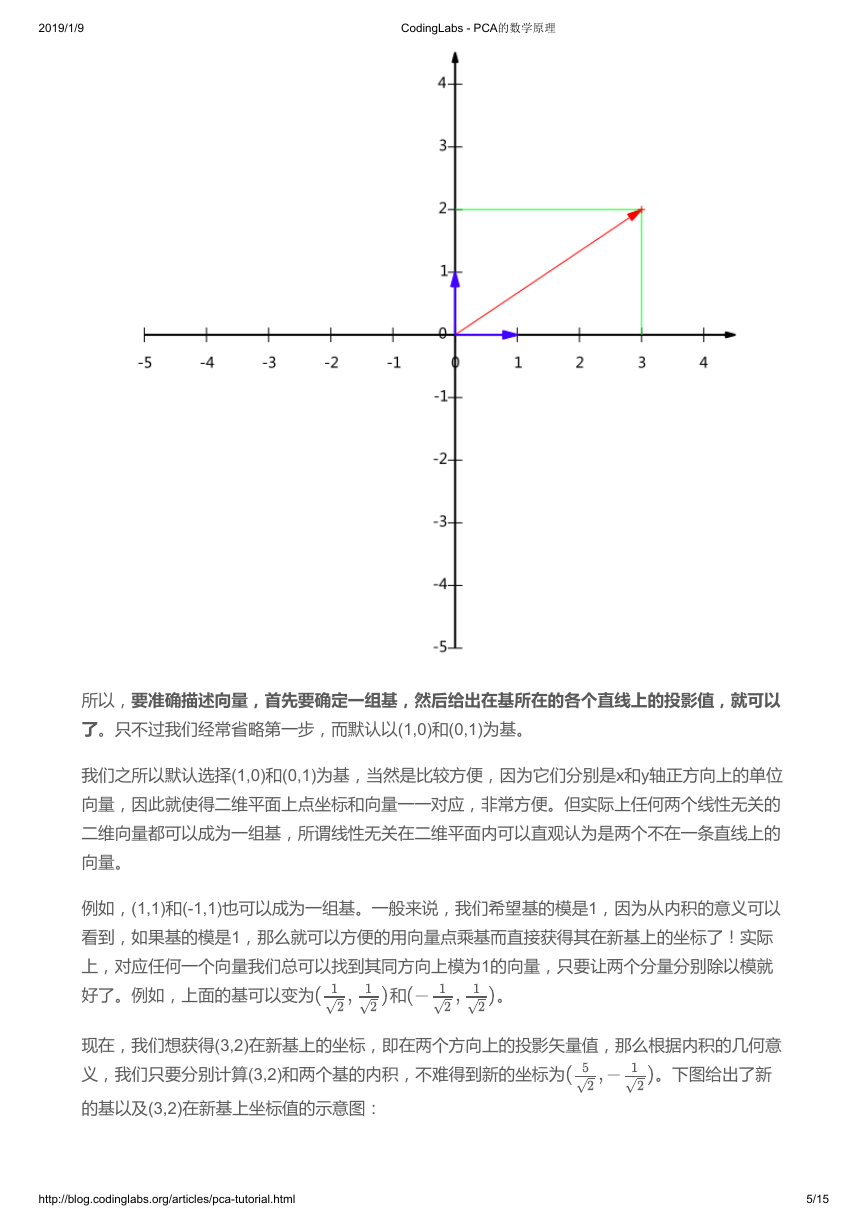
    2019/1/9 CodingLabs - PCA的数学原理 所以，要准确描述向量，首先要确定一组基，然后给出在基所在的各个直线上的投影值，就可以 了。只不过我们经常省略第一步，而默认以(1,0)和(0,1)为基。 我们之所以默认选择(1,0)和(0,1)为基，当然是比较方便，因为它们分别是x和y轴正方向上的单位 向量，因此就使得二维平面上点坐标和向量一一对应，非常方便。但实际上任何两个线性无关的 二维向量都可以成为一组基，所谓线性无关在二维平面内可以直观认为是两个不在一条直线上的 向量。 例如，(1,1)和(-1,1)也可以成为一组基。一般来说，我们希望基的模是1，因为从内积的意义可以 看到，如果基的模是1，那么就可以方便的用向量点乘基而直接获得其在新基上的坐标了！实际 上，对应任何一个向量我们总可以找到其同方向上模为1的向量，只要让两个分量分别除以模就 好了。例如，上面的基可以变为 和 。 现在，我们想获得(3,2)在新基上的坐标，即在两个方向上的投影矢量值，那么根据内积的几何意 义，我们只要分别计算(3,2)和两个基的内积，不难得到新的坐标为 。下图给出了新 的基以及(3,2)在新基上坐标值的示意图： http://blog.codinglabs.org/articles/pca-tutorial.html 5/15 ( , ) 1 2 √ 1 2 √ ( − , ) 1 2 √ 1 2 √ ( , − ) 5 2 √ 1 2 √
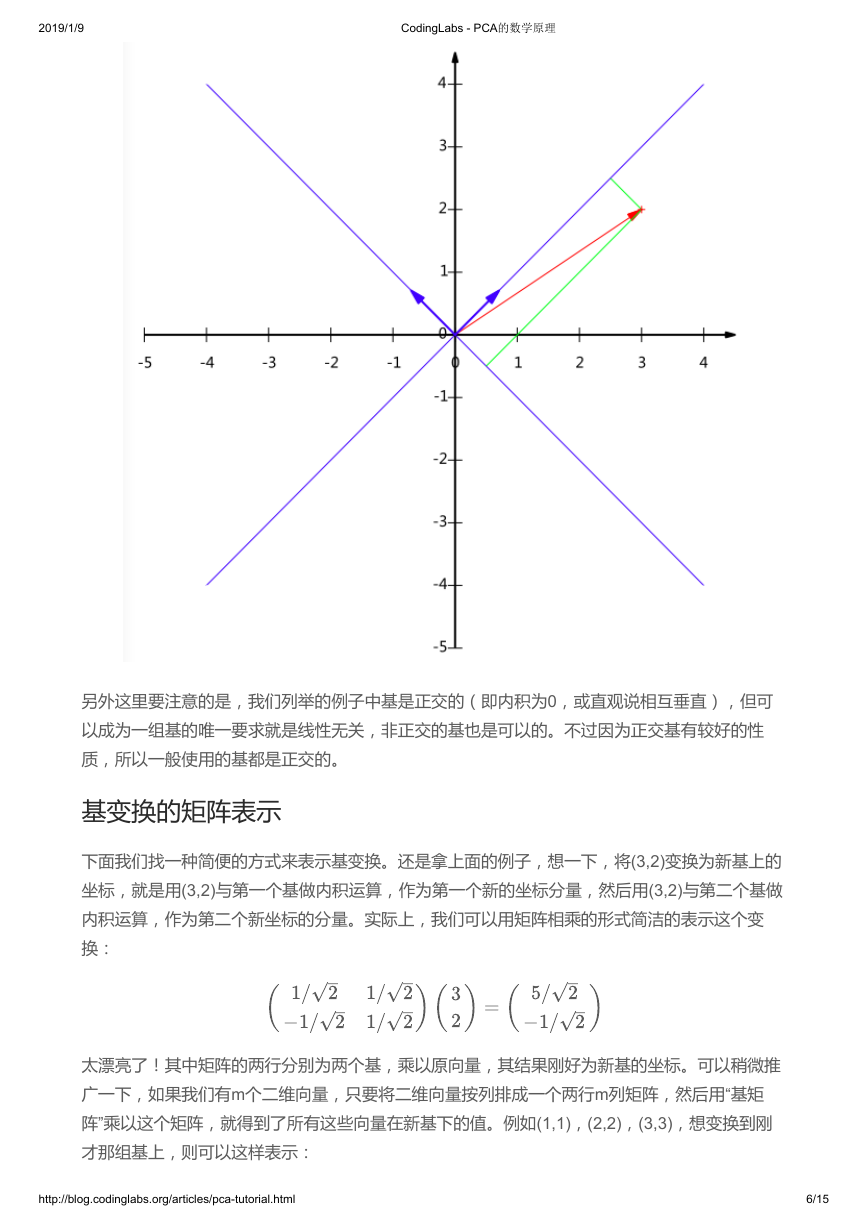
    2019/1/9 CodingLabs - PCA的数学原理 另外这里要注意的是，我们列举的例子中基是正交的（即内积为0，或直观说相互垂直），但可 以成为一组基的唯一要求就是线性无关，非正交的基也是可以的。不过因为正交基有较好的性 质，所以一般使用的基都是正交的。 基变换的矩阵表示 下面我们找一种简便的方式来表示基变换。还是拿上面的例子，想一下，将(3,2)变换为新基上的 坐标，就是用(3,2)与第一个基做内积运算，作为第一个新的坐标分量，然后用(3,2)与第二个基做 内积运算，作为第二个新坐标的分量。实际上，我们可以用矩阵相乘的形式简洁的表示这个变 换： 太漂亮了！其中矩阵的两行分别为两个基，乘以原向量，其结果刚好为新基的坐标。可以稍微推 广一下，如果我们有m个二维向量，只要将二维向量按列排成一个两行m列矩阵，然后用“基矩 阵”乘以这个矩阵，就得到了所有这些向量在新基下的值。例如(1,1)，(2,2)，(3,3)，想变换到刚 才那组基上，则可以这样表示： http://blog.codinglabs.org/articles/pca-tutorial.html 6/15 ( ) ( ) = ( ) 1 / 2 – √ − 1 / 2 – √ 1 / 2 – √ 1 / 2 – √ 3 2 5 / 2 – √ − 1 / 2 – √
    2019/1/9 CodingLabs - PCA的数学原理 于是一组向量的基变换被干净的表示为矩阵的相乘。 一般的，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R 个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB 的第m列为A中第m列变换后的结果。 数学表示为： 其中 是一个行向量，表示第i个基， 是一个列向量，表示第j个原始数据记录。 特别要注意的是，这里R可以小于N，而R决定了变换后数据的维数。也就是说，我们可以将一N 维数据变换到更低维度的空间中去，变换后的维度取决于基的数量。因此这种矩阵相乘的表示也 可以表示降维变换。 最后，上述分析同时给矩阵相乘找到了一种物理解释：两个矩阵相乘的意义是将右边矩阵中的每 一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。更抽象的说，一个矩阵可以 表示一种线性变换。很多同学在学线性代数时对矩阵相乘的方法感到奇怪，但是如果明白了矩阵 相乘的物理意义，其合理性就一目了然了。 协方差矩阵及优化目标 上面我们讨论了选择不同的基可以对同样一组数据给出不同的表示，而且如果基的数量少于向量 本身的维数，则可以达到降维的效果。但是我们还没有回答一个最最关键的问题：如何选择基才 是最优的。或者说，如果我们有一组N维向量，现在要将其降到K维（K小于N），那么我们应该 如何选择K个基才能最大程度保留原有的信息？ 要完全数学化这个问题非常繁杂，这里我们用一种非形式化的直观方法来看这个问题。 为了避免过于抽象的讨论，我们仍以一个具体的例子展开。假设我们的数据由五条记录组成，将 它们表示成矩阵形式： 其中每一列为一条数据记录，而一行为一个字段。为了后续处理方便，我们首先将每个字段内所 有值都减去字段均值，其结果是将每个字段都变为均值为0（这样做的道理和好处后面会看 http://blog.codinglabs.org/articles/pca-tutorial.html 7/15 ( ) ( ) = ( ) 1 / 2 – √ − 1 / 2 – √ 1 / 2 – √ 1 / 2 – √ 1 1 2 2 3 3 2 / 2 – √ 0 4 / 2 – √ 0 6 / 2 – √ 0 ( ) = ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ p 1 p 2 ⋮ p R ⎞ ⎠ ⎟ ⎟ ⎟ ⎟ a 1 a 2 ⋯ a M ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ p 1 a 1 p 2 a 1 ⋮ p R a 1 p 1 a 2 p 2 a 2 ⋮ p R a 2 ⋯ ⋯ ⋱ ⋯ p 1 a M p 2 a M ⋮ p R a M ⎞ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ p i a j ( ) 1 1 1 3 2 3 4 4 2 4
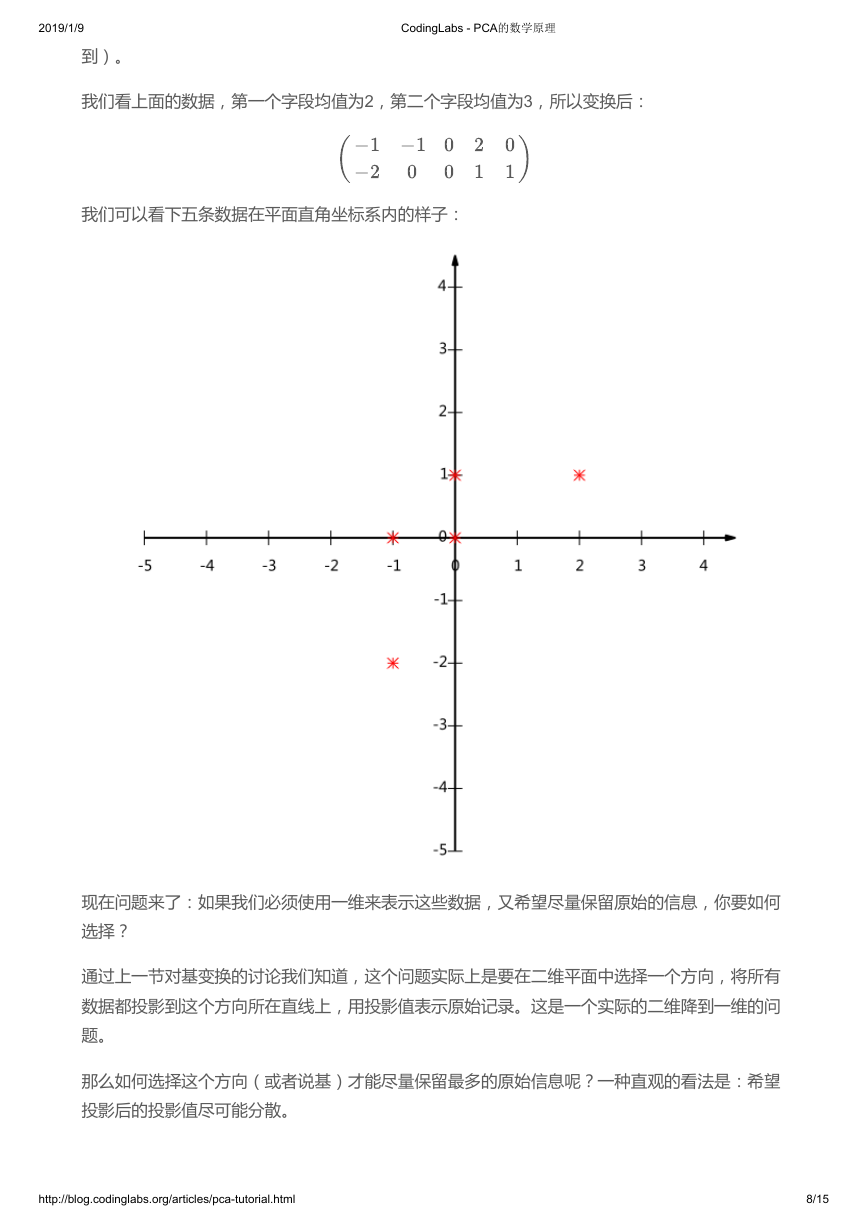
    2019/1/9 到）。 CodingLabs - PCA的数学原理 我们看上面的数据，第一个字段均值为2，第二个字段均值为3，所以变换后： 我们可以看下五条数据在平面直角坐标系内的样子： 现在问题来了：如果我们必须使用一维来表示这些数据，又希望尽量保留原始的信息，你要如何 选择？ 通过上一节对基变换的讨论我们知道，这个问题实际上是要在二维平面中选择一个方向，将所有 数据都投影到这个方向所在直线上，用投影值表示原始记录。这是一个实际的二维降到一维的问 题。 那么如何选择这个方向（或者说基）才能尽量保留最多的原始信息呢？一种直观的看法是：希望 投影后的投影值尽可能分散。 http://blog.codinglabs.org/articles/pca-tutorial.html 8/15 ( ) − 1 − 2 − 1 0 0 0 2 1 0 1
    分享到：
    赞 收藏

    相关推荐

    资料库

    大数据

    共收录841份资料，累计11个分类，关注成员有19位，主要包括：Matlab,统计分析,数据挖掘,Hbase,Hive,flink,kafka,spark,Storm,算法与数据结构,Hadoop

    热门标签

    Matlab 统计分析 数据挖掘 Hbase Hive flink kafka spark Storm 算法与数据结构 Hadoop

    最新资料