logo资料库

数字信号处理DTFT、DFT、FFT、加窗误差分析.doc

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.37M 资料格式：doc 举报 版权申诉
第1页 / 共27页
第2页 / 共27页
第3页 / 共27页
第4页 / 共27页
第5页 / 共27页
第6页 / 共27页
第7页 / 共27页
第8页 / 共27页
资料共27页，剩余部分请下载后查看
    汕 头 大 学 工 学 院 三 级 项 目 报 告 课程名称： 数 字 信 号 处 理 课程设计题目： 数字谱分析实践及误差讨论 指导教师： 姜 永 权 系 别： 电子工程系 专 业： 电子信息工程 学 号： 09142005 姓 名： 邓桂辉 合 作 者 完成时间： 2011 年 9 月 12 日至 10 月 26 日 成绩： 评阅人：姜永权 1 概述
     数字谱分析的意义 数字谱分析算法是 DSP 的基础算法，DFT 的高效的计算方法是快速傅立叶变换 FFT， DFT 的周期卷积特性是序列的循环卷积和离散时间系统（数字滤波器）分析 的基础。  项目完成内容简介 该项目一方面，总结了 CTFT、DTFT、CTFS、DTFS 四种算法的特点和它们之间 的联系，理论简述加窗效应和 DFT 与 FFT 算法。通过 matlab 画图对加窗 DTFT 的分 辨力和频谱泄露这两方面进行形象的分析，并就 DFT/FFT 计算分辨力和栅栏效应进 行仿真讨论。  结论与收获 数字谱分析算法是数字信号处理的基础，充分地结合 matlab 以达到从不同方面。 2 数字谱分析算法 2.1 四种傅氏变换的特点  CTFT 在数值计算中的困惑 x (t) a CTFT   )  X ( ICTFT    ( ) x t e a t   j dt （2.1.1） CTFT 虽然揭示了理想时间信号的时频对应关系，但无法进行数值计算，且其算法的 实时性也无法保证。  DTFT 在数值计算中的困惑 x a 抽样  ( ) x n d DTFT   IDTFT ( X e d j )     n  ( ) x n e d  j n  （2.1.2） DTFT 有两大计算限制：一，若 X(n)是无限序列，那么 DTFT 计算每个频率上的 )j dX e  是数字频率的 都需要无限多次的加法和乘法运算；二，由于 ( )j dX e  )j dX e  ( ( 连续函数，所以必须在所有频率上计算 ( 的计算式完全不可能的。 )j dX e  。所以在通常情况下要实现对 DTFT  CTFS 与 DTFS 的启示 CTFS：CTFT 和 CTFS 都相当于讲一个信号表示为一组复指数信号线性组合，连续周 期信号 CTFS 是连续非周期 CTFT 上的那些复数成谐波关系地出现在离散点 0k ，
    k=0,1,2,3…上的值。所以，CTFS 把周期性连续信号与离散频率函数 起了。 DTFS：DTFT 和 DTFS 都相当于讲一个信号表示为一组复指数信号线性组合，离散周 期序列 DTFS 是离散非周期序列 DTFT 上的在一个周期内的取样。将有限长时间序列 看作无限长时间序列的一个周期，就可以进行 DTFS 变换。 0 ( X k 联系在一 )  DFT 算法的给出 DFT 是为克服 DTFT 局限而提出的切实可行的数值计算方法。 ( ), x n n  0,1,2,3,4 … DFT  ( ) X k  ( X e j (2  / k N ) )  N 1  ( ) x n e  n  0 j (2  / k N ) ,0   k N  1  FFT 算法的作用与意义 直接按照式计算 DFT，当信号数据量很大时，需要很大的计算量。FFT 算法的基 NW 的对称 本思想是，把 N 点 DFT 不断分解成点数更小的 DFT，同时利用旋转因子 性和周期性来简化计算，它具有与 DFT 完全相同的性质，其计算结果也是准确的等 于 DFT 的。 nk 2.2 时窗效应  时域加窗处理的必要性 加窗将无限长序列阶段成一小段长为 N 的离散序列才能实现 DTFT 计算。加窗能 根据实际工程需要近似等到无限长序列的频谱。 加窗 DTFT 算： ( X e N )= j  ) W( j   e ) j  （2.2.1） ( ) x n N   ( ) ( ) x n w n 1 2  ( X e  时域加窗处理的误差定性分析 一是计算出的频谱中出现有多余的高频分量，这是由于窗函数突然截断信号无限 离散信号而引起的，称这种现象为频谱泄露；二是谱线变成了据有一定宽度的谱峰， 从而降低了频率的分辨力。  窗函数种类及性能分析
    矩形窗: R ( ) 1,0 w n    n N  1 Hamming 窗: HAMw ( ) 0.54 0.46cos(1 n    2  n 1 N  ),0   n N  1 HANw Hanning 窗: ( ) 0.5(1 n  ( ) w n TRI  ( ) w n TRI             2( 2( 三角形窗： Blackman:  2  1 N  2 , n N +1) , N n  N n ),0   n N  1 0   n N 2 N 2 1    n N ( N 为偶数 ) n 0   2 ( +1 2 , n N ） 1 N  +1) ,( +1) 2 1 N n    +1 N N n N  （n为奇数） w BLK ( ) 0.42 0.5cos( n   2  1 N  n ) 0.08cos(  4  1 N  n ), 0   n N  1 （2.2.2） （2.2.3） （2.2.4） （2.2.5） （2.2.6） I 0     1 (1   2 n N  2 ) 1    ,0   n N  1 ( ) w n K  ( ) w n K  Kaiser 窗： I 0     ( I N  0 1  ) 2  (    I 0    2  ( n  1 ) 2 N  2 1 ) 2 N  2    ,0   n N  1 （2.2.7） 六种窗主瓣宽度增加的顺序为：矩形窗、Kaiser 窗、三角形窗、Hamming 窗、 Hanning 窗和 Blackman 窗。旁瓣幅度由到小的顺序是矩形窗、三角窗、Kaiser 窗、 Haning 窗、Hamming 窗和 Blackman 窗。矩形窗的主瓣最窄，但旁瓣幅度最大， R=-13.46dB。一般认为 Hamming 窗是最好的，R=-40dB，主瓣宽为矩形窗的主瓣宽 的两倍。  物理分辨力与频谱泄露量的定量分析 w R  矩形窗频谱:   n  ( ) w n e  j n   1 L   n  0  j n  e  1 e  1 e   jN   j   sin( sin( / 2) L  / 2)  e  j  ( L  1)/2 （2.2.8）
    矩形窗零点：   1 2  L , 2  2  , L …， k 2  L ，…  w  2  L ， f   w f s L  1 LT  1 T L 主瓣宽： ( ) w  (0) w 主旁瓣相对高度： sin( L  sin( L  / 2) / 2)  sin(3 / 2) sin(3 / 2 ) L   L  L    3 R  20log 10 ( ) w  (0) w 对数表示：  20log 10 L 2 3    13.46 dB    3 时域加窗在频域的计算： LX ( )   1 2  X ( )   W  ) ( （2.2.9） （2.2.10） （2.2.11） 对单一频率的虚指数： ( ) x n  e j  0 n X L ( )   1 2  X (     0 )= ( W W   ) ( ) （2.2.12） 原来无限长序列的理想频谱线 ( X  ，被按照矩形窗的形状扩展到整个频域范围。矩 ) 形窗谱 ( RW  的主瓣宽度限制区分两个相邻的频率成分的能力， )    f   频率分辨力定义为： rad ) 2 (  N   2  f  s   2 T  s  1 NT s  f s N ( Hz ) （2.2.13） 2.3 DFT 与 FFT 算法  广义 DFT 算法与传统 DFT 算法的区别联系  X k d   N 1   n  0  j 2  N kn   x n e , k  0,1,.... N  1 （2.3.1） DFT 是离散付氏变换，而 DTFT 是连续频谱的傅里叶变换。DTFT 是单位圆上的 Z 变 换，而 DFT 是单位圆上从零开始，2π/N 为间隔对 DTFT 的均匀抽样。  计算分辨力的概念与定量分析
     bin  2  N or  f bin  f s N 计算分辨力定义为 N≥L 不会产生混叠 DFT 和 DTFT 反变换结果相同； N
    X m [ ]     [2 ] X m [2 X m  1] （2.3.4） 3 计算举例与分析讨论 3.1 加窗处理造成的频谱泄露  画出单频信号加不同窗函数处理后的时域波形图，编程计算加窗信号的 DTFT 频谱，分别画出相应的幅度谱图（不同窗函数） 用 1  sf kHz 的采样信号对   x t  理论分析： cos(2  f t 0 ) , f 0  50 z H 进行采样，并进行加窗处理。 ( ) x n  cos( f     ), 2 n 0 0 f s 0  0.1  rads sample / ， 0,1,2, n  …,L-1 ( ) x n L  ( ) ( ) w n x n res  ( ) x n L  w ham ( ) ( ) n x n  ) n  0 cos(  0.54 0.46cos    2        1 L   cos ( n  0 ) 根据式（2.2.8）和(2.2.12)知原来无限长序列的理想频谱线 ( X  ，被按照矩形窗和 Hamming 窗的形状扩展到整个频域范围，出现频谱的主瓣和旁瓣，但两种加窗谱有不同 ) 主瓣宽和旁旁瓣幅度。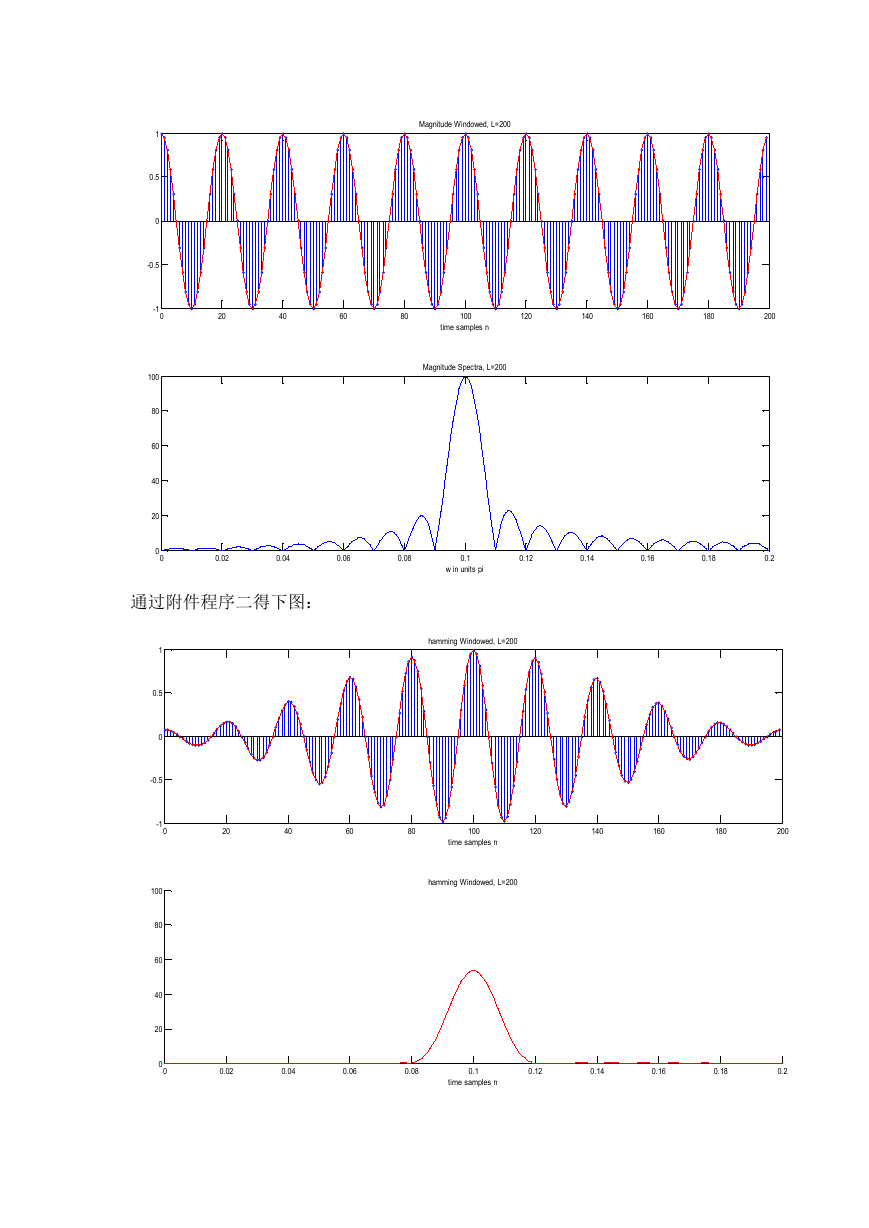 通过附件程序一得下图：
    1 0.5 0 -0.5 -1 0 100 80 60 40 20 0 0 Magnitude Windowed, L=200 20 40 60 80 100 time samples n 120 140 160 180 200 Magnitude Spectra, L=200 0.02 0.04 0.06 0.08 0.1 w in units pi 0.12 0.14 0.16 0.18 0.2 通过附件程序二得下图： 1 0.5 0 -0.5 -1 0 100 80 60 40 20 0 0 hamming Windowed, L=200 20 40 60 80 100 time samples n 120 140 160 180 200 hamming Windowed, L=200 0.02 0.04 0.06 0.08 0.1 time samples n 0.12 0.14 0.16 0.18 0.2
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料