求解TSP量子蚁群算法.doc

发布时间：2022-06-19 发布人：admin 分类：说明书资料大小：0.65M 资料格式：doc 举报版权申诉

b47a6c06-0f04-404e-9bd3-d0d0fe1afd86.doc.pdf-第1页.png

第1页 / 共8页

b47a6c06-0f04-404e-9bd3-d0d0fe1afd86.doc.pdf-第2页.png

第2页 / 共8页

b47a6c06-0f04-404e-9bd3-d0d0fe1afd86.doc.pdf-第3页.png

第3页 / 共8页

b47a6c06-0f04-404e-9bd3-d0d0fe1afd86.doc.pdf-第4页.png

第4页 / 共8页

b47a6c06-0f04-404e-9bd3-d0d0fe1afd86.doc.pdf-第5页.png

第5页 / 共8页

b47a6c06-0f04-404e-9bd3-d0d0fe1afd86.doc.pdf-第6页.png

第6页 / 共8页

b47a6c06-0f04-404e-9bd3-d0d0fe1afd86.doc.pdf-第7页.png

第7页 / 共8页

b47a6c06-0f04-404e-9bd3-d0d0fe1afd86.doc.pdf-第8页.png

第8页 / 共8页

1 引言

2 TSP简述

3 混合量子蚁群算法(HQACA)

3.1 量子信息编码

3.2 信息素更新规则

3.3 变换邻域准则

3.4 HQACA算法步骤

4仿真实验和分析

6 结束语

求解旅行商问题的混合量子蚁群算法摘要：针对蚁群算法求解旅行商问题时易陷入局部最优和收敛速度慢的问题，提出一种新的求解旅行商问题的混合量子蚁群算法。该算法采用量子比特的概率幅对各路径上的信息素进行编码，量子旋转门及蚂蚁走过的路径对信息素进行更新，加快算法收敛速度；为了避免搜索陷入局部最优，设计一种新的变换邻域准则，以提高求解效率。TSPLIB 中部分实例仿真结果表明该算法比传统蚁群算法具有更快的收敛速度和求解精度。关键词：量子蚁群算法；变换邻域准则；旅行商问题 Hybrid Quantum Ant Colony Algorithm for Traveling Salesman Problem Abstract： Aiming at the Traveling Salesman Problem based on ant colony optimization which is easy to fall into local optimums and has a slow convergence rate，a hybrid quantum ant colony optimization algorithm is presented .In this algorithm，the pheromone on each path is encoded by a group of quantum bits, the quantum rotation gate and ant’s tour are used to update the pheromone so as to accelerate its convergence speed; To avoid the search falling into local optimum, the new neighborhood exchange strategy is designed to improve solution efficiency. Some cases from the TSP library(TSPLIB) are used to experiment, the results show that the algorithm has rapider convergence speed and higher accuracy than the classical ant colony algorithm. Key words: Quantum Ant Colony Algorithm; neighborhood exchange strategy ; Traveling Salesman Problem 1 引言蚁群算法是一种模拟进化算法，最早是意大利学者Dorigo M 于1991 年提出 [1] ，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为，算法成功地用于TSP求解、工件排序、图着色、车辆调度等多目标组合优化问题  2 7 。然而,迭代次数多、收敛速度慢、易于陷入局部最优解仍是制约ACO算法广泛应用的主要瓶颈。  量子计算  8 的研究开始于二十世纪八十年代，Benioff 和 Feynman 提出了量子计算的概念。量子计算利用量子理论中有关量子态的叠加、纠缠和干涉等特性，用来解决经典计算中的许多难题，并以其独特的计算性能引起科技界的广泛关注。1985 年 Deutsch 指出，利用量子态的相干叠加性可以实现并行的量子计算。1994 年 Shor 提出大数因子分解的量子算法，此算法可在量子计算机上以多项式时间实现，它使 NP 问题变成 P 问题。2002 年， Kuk-Hyun Han 等提出量子进化算法(Quantum-InspiredEvolutionary Algorithm, QEA)，它是一种基于量子计算原理的概率优化方法。它以量子计算的一些概念和理论为基础，用量子位编码来表示染色体，用量子门作用和量子门更新来完成进化搜索，具有种群规模小而不影响算法性能、同时兼有“勘探”和“开采”的能力、收敛速度快和全局寻优能力强的特点  9 。量子蚁群算法（Quantum Ant Colony Algorithm，QACA）则将量子计算和蚁群算法相结合，把量子计算中的态矢量和量子旋转门引入到蚁群算法中，加快了算法的收敛速度。量子蚁群算法已成功地求解许多组合优化问题，文献[10]使用量子蚁群算法对0-1背包问题（0/1 knapsack problem）进行求解，并用数值试验说明了算法的有效性。文献[11]利用量子计算

的并行性，将量子蚁群算法用于求解多任务联盟问题，并取得了较好的结果。文献[12]中分析了量子蚁群算法的优缺点，提出一种新的量子蚁群算法用于求解小规模旅行商问题（Traveling Salesman Problem，TSP），但对于求解较大规模问题时，该算法易陷入局部最优和停滞状态。针对量子蚁群算法求解TSP问题的不足，本文提出一种混合量子蚁群算法（Hybrid Quantum Ant Colony Algorithm，HQACA），该算法设计了一种新的变换邻域准则来对求得的解进行优化，扩大解的搜索空间，改善种群信息结构，避免搜索陷入局部最优。对国际通用的TSPLIB中部分实例进行了实验, 并将该算法与目前比较常用的一些算法进行了比较, 仿真结果表明该算法具有更好的收敛速度和求解精度。 2 TSP 简述直观地说，TSP问题就是指一位商人，从自己的家乡出发，希望能找到一条最短路径， j  ,i 途径给定的城市集合中的所有城市，最后返回家乡，并且每个城市都被访问且仅访问一次。形式上，TSP问题可以用一个带权完全图G=(N,A)来描述，其中N是城市的结点集合，A是所有边的集合。每一条边 A 都分配一个权值 ijd ，它代表城市i与j之间的距离大小，其中 ,i j N 。在非对称TSP中，一对结点i,j之间的距离与该边的方向有关，也就是说，至少存在一条边 d 。TSP的目标就是寻找图中的一条具有最小成本值的哈密尔顿回路，这里的哈密尔顿回路是指一条访问图G中的每一个结点一次且仅一次的闭合路径。这样，TSP的一个最优解就对应于结点标号为 d 。在对称TSP中，集合A中所有的边都必须满足 ij d f  的定义为：  j ，有 ij d ,i 1,2,...,n 的一个排列，并且使得长度  f  最小。     ji ji f     n 1   i 1  d   ( ) i ( 1) i   d   ( ) n (1) （1）求解TSP问题最直接同时也是最精确的方法就是穷举搜索，将n个城市的任意排列看作一个有序表，它决定了所访问的城市的顺序，旅行商从某个城市出发，然后历经所有城市直至到出发城市，每个有序表都对应一个路径长度总耗费，由于每一条路径可能用2n种不同表示方法，而n个城市排列数为n!，因此搜索空问大小为 S  n ! 2 n   n   1 ! 2 。穷举搜索算法就是计算 n  1 ! 2 个不同的有序表的耗费，其中最小耗费对应的旅行路经就是TSP的解，随着城市数目的不断增加，求解空间将呈指数级增长，通过穷举法根本无法求解，因此用优化算法解决TSP就十分必要。目前, 求解 TSP 问题的算法较多, 最常用的方法主要有神经网络算法、蚁群算法、启发式搜索法、遗传算法、模拟退火算法和量子算法等。这些算法在求解TSP时有各自的优点和缺陷，有的运算快但易于收敛到局部最优解，有的求解精度高但收敛速度较慢，有的求解城市规模较小等，针对以上算法的不足，本文使用一种混合量子蚁群算法来求解TSP。 3 混合量子蚁群算法(HQACA) 3.1 量子信息编码在经典计算中，采用 0 和 1 二进制表示信息，称为比特。在量子信息论中，信息的基本存储单元是量子比特，或称量子位。一个简单的量子比特是一个双态系统，它的两个极化状态对应经典信息的二进制存储单元状态的 0 和 1。区别于经典比特，一个量子比特除了可以处于 0 态和 1 态之外，还可以处于它们的叠加态。 2

一个量子位可以使用概率幅         表示，那么有 n 个量子位的个体概率幅可表示为： 1 ... ...  n  n    2      1 2 其中， i、 i满足     2  ，i=1,2,…,n，该量子个体可以表示任意量子叠加 1 （2） 2   i i 态。在 HQACA 中，使用量子比特表示各路径上的信息素，第 k 只蚂蚁在各路径上的量子信息素编码可表示为：         11    11   21    21 Q  k   12    12   22    22           1 n    1 n      n    n 2 2                       ij    ij       1 n    1 n   2    2 n n          nn    nn                  （3）   ij    ij j 时，  ；当i    1 其中，n 为城市总数目，表示城市 i 到城市 j 之间路径上的信息素的概率幅，当 2 2 ij   ij i j 时，  。对于城市 i 和 j，当有蚂蚁通过 i 到 j 的路径，会使得该路径上信息素概率幅 ij 的值增大，信息素得以增强；反之，该路径上的信息素会有所挥发，信息素更新规则见 3.4 节。   ij   n i j ij , 2 2  0 1  3.2 信息素更新规则按照 TSP 约束，当所有蚂蚁都构建好路径后，各边上的信息素将会被更新。首先，所有边上的信息素都会减少一个常量因子的大小，然后在蚂蚁经过的边上增加信息素。信息素的蒸发根据下面的公式执行 , j  ij 其中 是信息素的蒸发率，有 0  1     ij   A   i , 1  ，参数的作用是避免信息素的无限积累。在（4）信息素的蒸发步骤之后，所有蚂蚁都在它们经过的边上释放信息素：   ij ij   m  k 1  k    ij ,  i ,  j  A 其中 k    k     ij  2 k  ij    1 ij 是第 k 只蚂蚁向它经过的边释放的信息素量。 k ij 定义为 k C  ，如果边  i ,  j 在第只蚂蚁构建的路径上 k T k 0 否则 3 （5）（6）

其中 k ij 表示第 k 只蚂蚁在 i 到 j 的路径上的量子信息素强度，  ； kC 表示第 k 只蚂蚁建立的路径 kT 的长度，即在 kT 中所有边的长度之和；表示量子信息素启发因子，表示 i 到 j 路径上量子态概率幅的相对重要性。 k   ij 1 设有m只蚂蚁， n n 的矩阵R是n个城市TSP问题的一条解路径，它满足每行每列有且仅 k ij 2 2 有一个元素为1，其余为0.R[i,j]=1表示路径R中存在从城市i到城市j的边，当i=j时必有 R[i,j]=0。算法中采用矩阵 , kR k  1,2,..., m 记录第k只蚂蚁求得的路径， bestR 记录运算过程中所求得的最优解，使用量子旋转门更新蚂蚁在各路径上的量子概率幅，量子旋转门的调整方式为：   sin     cos                cos sin 1  t   ij   1 t    ij 式中，i,j=1,2,3,…,m,      T  t  ij   t   ij     （7） ij  为第t次迭代中城市i到城市j之间路径上的信息素的概率 t ij , t 幅，表示路径i到j的量子位的旋转角度，如表1  13 中的 ij ，其值通过查表所得到，用于控制算法的收敛速度。 ,R i  j bestR  , j i  f R   表1 旋转角策略  ij  f R best  s   ij ,ij  ij  ij 0 ij  ij 0 ij  0 ij  0 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 假真假真假真假真 0 0 0 0 0 0 0.05π -1 0.01π -1 0.025π 1 0.005π 1 0.025π 1 0 0 0 1 1 -1 -1 -1 0 0 0 0 0 ±1 ±1 ±1 0 0 0 ±1 ±1 0 0 0 ,ij ij 在表1中，f(x)为目标函数，在本文中为蚂蚁建立的路径的长度；  s   表示旋转角  度的方向，用来保证算法的收敛性。 3.3 变换邻域准则所谓邻域搜索是只针对解空间中某个特定的区域进行搜索，搜索过程可用以下三步说明： 1．从解空间中找一个解并评估其质量，将它定义为当前解。 2．按照变换邻域准则变换当前解得到当前解的一个邻域，找出邻域中的最好解，定义该解为新解。 3．如果新解优于当前解，则将当前解用新解替换，重复第2步；否则，抛弃新解，停止 4

搜索。邻域搜索中最关键最困难在于如何变换当前解，得到当前解的一个领域，针对量子蚁群算法求解TSP问题，本文设计一种新的变换邻域准则来对蚂蚁求得的当前解进行优化，避免搜索陷入局部最优。定义：   S       1 ,..., , , , , 1 2 3 1 n n  为n个城市的TSP问题的一条路径， i 表示该路径第 i 个位置的城市序号，候选解 S 的k-变换邻域指的是从城市 1 到 n 经过的n-1条边中去除k条边，将原路径分成k+1个部分，对这k+1个部分重新排列而得到的解的集合。为了保证邻域中解的初始城市和结束城市与原路径相同，第一部分保持不变，后面k部分按排列的方式进行组合。 1)k-变换局部寻优对于路径S，断开其任意k条边，保持第一部分不变，后面k部分按排列方式进行组合生成新的路径，如果新生成的路径优于已知的最优解，则用当前路径替换最优路径，重复此过程直到搜索完邻域内所有的路径。如图1为2-变换局部寻优过程,图2为3-变换局部寻优过程。图1 2-变换局部寻优图2 3-变换局部寻优过程 2)时间复杂性分析对于n个城市的TSP问题，2-变换局部寻优的搜索空间大小是  ! 1 k nC  。一般而言当K     2 1 2! 1 nC    1 很小时，邻域搜索会较快结束，但解的质量不太高。相反，当K很大时，邻域中解的数目会随K呈指数级增长，虽然解的质量会有所提高，但搜索时间会很长，综合考虑解的质量和计，k-变换局部寻优的搜索空间大小  2 2  1 k     n n  5

算时间在实际应用K一变换局部寻优算法时，K一般取2或3。 3.4 HQACA 算法步骤 , 的值，蚂蚁个数为 m，最大迭代次数 NMAX，当步骤 1 初始化：设定各参数 , 1  .为了使算法初始搜索时所有状态以相同概率出现，蚂 , 前迭代次数 t=0 ，信息素  0 蚁量子信息素编码中所有的 ,ij ij ij  取值均为1 2 。步骤 2 设城市总数为 n，将 m 只蚂蚁随机的放在 n 个城市的其中一个上，每只蚂蚁独立的构造一个解，按照式(8)选择要访问的城市，重复地应用状态转移规则，直到蚂蚁 k 访问完所有的城市。 j      arg max     il il l N   k i   ，如果 q  q 0 （8） J 否则，代表边(i,l)的自启发量，是自启发量的权重， i 上式确定了该算法中蚂蚁 k 要访问的下一个城市 j，其中： il 为边(i,l)上的信息素浓度， =1il kN 代表了位于城市 i 的蚂蚁 k ild 可以直接到达的相邻城市的集合，也就是指所有还没有被蚂蚁 k 访问的城市的集合，J 是根据式（9）给出的概率分布产生出的一个随机变量。 k p ij              ij ij        il il l N  k i , 如果 j N  k i   （9） k ijp 指位于城市 i 的蚂蚁 k 选择 j 作为下一个访问城市的概率。和是两个参数，分别决定了信息素和启发式信息的相对影响力。 q 是均匀分布在区间[0,1]中的一个随机变量，  q 0 0 q 0  1  是一个参数，指蚂蚁选择当前可能的最优移动方式的概率，这种最优的移动方式是根据信息素的积累量和启发式信息值求出的。同时，蚂蚁以 1 q 的概率有偏向性地探索各条边。通过调整参数 0q ，我们可 0 以调节算法对新路径的探索度，从而决定算法是应该集中搜索至今最优路径附近的区域，还是应该探索其他区域。步骤 3 若 m 只蚂蚁都构造完成各自的解，则转步骤 4，否则转步骤 2。步骤 4 对 m 只蚂蚁生成的解使用 3-变换局部寻优算法进行优化，记录 m 只蚂蚁构造出来的最优解。步骤 5 根据当前最优解，应用量子旋转门规则 [10] 更新蚂蚁在各个路径上的量子信息概率幅，按照式 2 进行全局信息素更新。步骤 6 若满足结束条件，即t NMAX  ，输出最优解，否则 t=t+1，转步骤 2。 4 仿真实验和分析本文测试用例来自国际通用的TSP实例库TSPLIB  14 ，选用att48、ch150、kroa100进行 6

实验仿真，并将HQACA与ACS（基本蚁群算法）、SAS（排序蚁群算法）和MMAS（最大最小蚁群算法）进行对比实验，以验证所提算法的有效性和可行性。对每个实例分别用 HQACA、ACS、SAS、MMAS做50次独立的测试，城市间距离保留小数，并记录下50次实验中各算法找到的最好解、最差解、平均最好值。运行参数：蚂蚁数m=50，     1,  5,  ，量子启发因子 2 ~ 4  0.9 ，先验知识 0 q  0.01 。表1：att48对比实验结果已知最优解 33522 算法 ACS SAS MMAS HQACA 最大进化代数 2000 2000 5000 1000 平均进化代数 927.37 839.8 2449.15 447.75 所求最好解 33739 33522 33522 33522 所求最差解 35116 34533 34228 33966 平均值 34614.32 33734.2 33772.65 33691.45 表2：kroa100对比实验结果已知最优解 21282 算法 ACS SAS MMAS HQACA 最大进化代数 3000 3000 8000 3000 平均进化代数 1791.63 1226.85 3751 836.85 所求最好解 22454 21409 21282 21282 所求最差解 22970 22336 22291 21672 表3：ch150对比实验结果算法已知最优解平均值 22670.1 21594 21589.8 21453.4 平均值最大进化代数 5000 5000 10000 5000 平均进化代数 3649.67 1409.1 6929.2 1333.65 6528 ACS SAS MMAS HQACA 6756.33 6668.45 6609 6594.3 从表1~表3中可以看出，当问题规模较小时，SAS、MMAS、HQACA三种算法均能求出最优解，本文提出的HQACA算法的收敛速度优于SAS和MMAS算法，随着问题规模的增大， SAS收敛速度优于MMAS算法，MMAS求解精度优于SAS算法，HQACA算法的收敛速度和求解精度都优于MMAS和SAS算法，实验表明了HQACA算法比MMAS和SAS算法更稳定，具有较强的鲁棒性。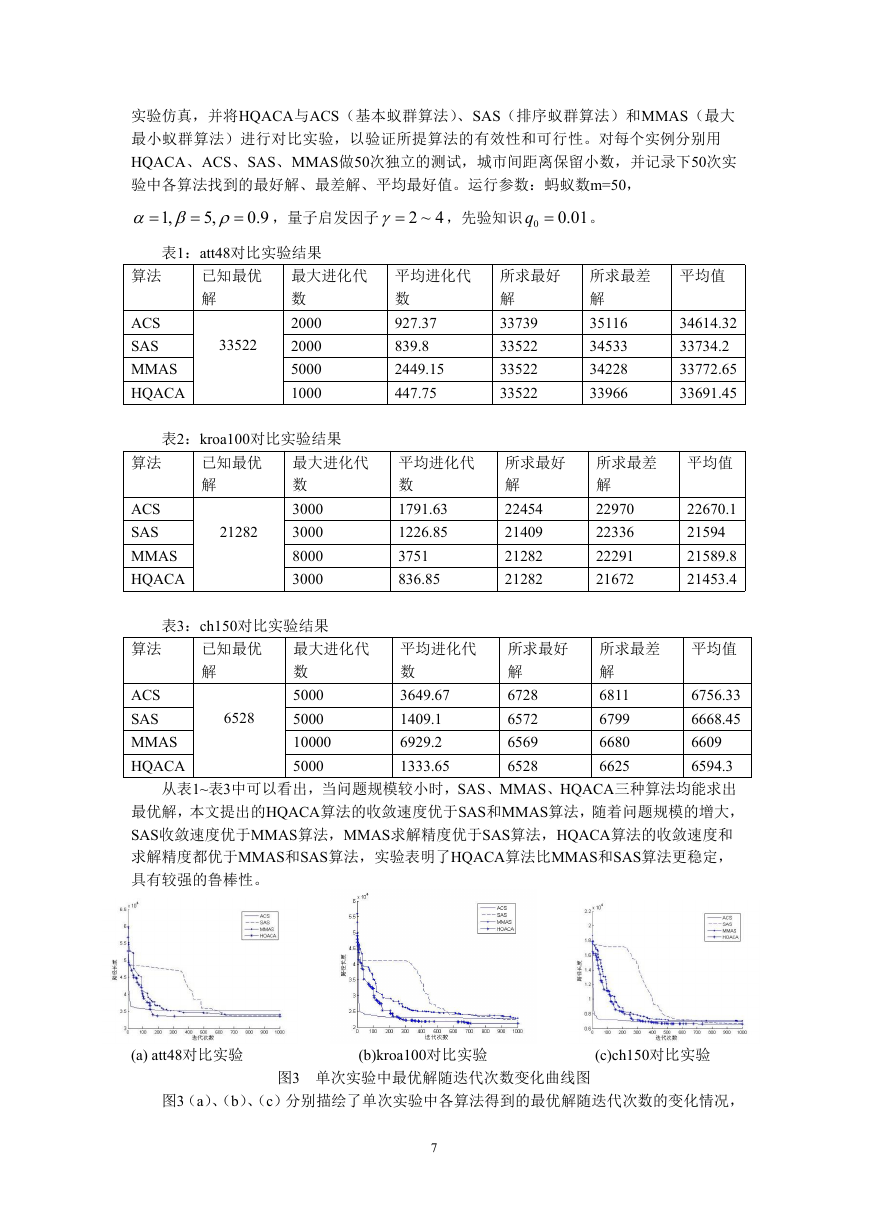所求最好解 6728 6572 6569 6528 所求最差解 6811 6799 6680 6625 (a) att48对比实验 (b)kroa100对比实验 (c)ch150对比实验图3 单次实验中最优解随迭代次数变化曲线图图3（a）、（b）、（c）分别描绘了单次实验中各算法得到的最优解随迭代次数的变化情况， 7

为了便于观察，我们取迭代次数为1000，从图中可以看出，传统的ACS算法虽然收敛速度较快，但容易早熟，陷入局部最优解，SAS和MMAS虽然求解精度高于ACS，但是收敛较慢， HQACA算法则弥补了传统算法的不足，既能保证求解的精度，又能快速的收敛。实验表明了对信息素进行量子比特编码，能够增加解的多样性，有助于勘测和开采到更多更好的解，避免算法过早出现停滞现象；采用量子旋转门作为进化策略，能够加快算法收敛，提高全局搜索能力，针对有可能陷入局部最优问题，对蚂蚁每次求得的解进行邻域变换，扩大搜索区域，寻求更好质量的解。 6 结束语本文将量子蚁群算法与邻域搜索相结合，提出了一种求解 TSP 问题的混合量子蚁群算法。算法采用量子比特对 TSP 问题中各路径上的信息素进行编码，并对蚂蚁求得的解进行邻域变换，扩大搜索空间，加速算法收敛。将 HQACA 算法与其他传统算法进行仿真比较，结果证明了该算法求解 TSP 问题的有效性和可行性，在以后的研究中将进一步研究 HQACA 算法以解决更为实际的问题，扩大该算法的应用领域。参考文献 [1] Colorni A, Dorigo M, Maniezzo V, et al. Distributed optimization by ant colonies [C]// Proceedings of the 1st European Conference on Artificial Life. Paris, France: Elsevier Publishing, 1991: 134-142. [2] 申铉京,刘阳阳,黄永平,徐铁,何习文.求解 TSP 问题的快速蚁群算法[J].吉林大学学报, 2013, 43 (1): 147-151. [3] 张洁,张朋,刘国宝.基于两阶段蚁群算法的带非等效并行机的作业车间调度[J].机械工程学报, 2013, 49(6): 136-144. [4] 王欣盛,马良.工件排序的改进蚁群算法优化[J].上海理工大学学报, 2011, 33(4): 362-366 [5] 朱庆保,扬志军.基于变异和动态信息素更新的蚁群优化算法[J].软件学报, 2004, 15(2): 185-192 [6] 陈英武,姚锋，李菊芳,贺仁杰,邢立宁.求解多星任务规划问题的演化学习型蚁群算法[J].系统工程理论与实践, 2013, 33 (3): 791-801. [7] 刘霞，扬超.最小-最大车辆路径问题的蚁群算法[J].解放军理工大学学报, 2012, 13(3): 336-341 [8] Han K H,Kim J H.Genetic quantum algorithm and its application to combinatorial optimization problem [C]. Proceedings of the 2000.IEEECongress on Evolutionary Computation,2000:1354-1360. [9] Han Kuk-Hyun and Kim Jong-Hwan. Quantum-inspired Evolutionary Algorithm for a Class of Combinatorial Optimization. IEEE Transactions on Evolutionary Computation, IEEE Press, 2002, 6(6): 580~593. [10] 何小锋，马良.求解 0-1 背包问题的量子蚁群算法[J].计算机工程与应用，2011，47（16）：29-31. [11] 翼俊忠，程亮，赵学武，刘椿年.量子蚁群算法求解多任务联盟问题[J].北京工业大学学报，2013,39 （3）：412-419. [12] 赵俊生，李跃光，张远平.一种改进的量子蚁群算法及其应用[J].计算机应用与软件，2010，27（7）： 133-135. [13] Li B B,Wang L.A hybrid quantum-inspired genetic algorithm for multi-objective flow shop scheduling[j].IEEE Transactions on Systems,Man and Cybemetics,2007,37(3):576-591. [14] REINELT G.TSPLIB[DB/OL]: http://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/, 2006. 8

分享到：

赞收藏

资料库

求解TSP量子蚁群算法.doc

相关推荐

人工智能

热门标签

最新资料