Deep Plug-and-Play Super-Resolution for Arbitrary Blur Kernels_注....pdf

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：5.50M 资料格式：pdf 举报版权申诉

qq_40994260-12016236-4744300845193775972.pdf-第1页.png

第1页 / 共11页

qq_40994260-12016236-4744300845193775972.pdf-第2页.png

第2页 / 共11页

qq_40994260-12016236-4744300845193775972.pdf-第3页.png

第3页 / 共11页

qq_40994260-12016236-4744300845193775972.pdf-第4页.png

第4页 / 共11页

qq_40994260-12016236-4744300845193775972.pdf-第5页.png

第5页 / 共11页

qq_40994260-12016236-4744300845193775972.pdf-第6页.png

第6页 / 共11页

qq_40994260-12016236-4744300845193775972.pdf-第7页.png

第7页 / 共11页

qq_40994260-12016236-4744300845193775972.pdf-第8页.png

第8页 / 共11页

文本预览

Deep Plug-and-Play Super-Resolution for Arbitrary Blur Kernels Kai Zhang1,2, Wangmeng Zuo1,3,∗, Lei Zhang2,4 1School of Computer Science and Technology, Harbin Institute of Technology, Harbin, China 2Dept. of Computing, The Hong Kong Polytechnic University, Hong Kong, China 3Peng Cheng Laboratory, Shenzhen, China 4DAMO Academy, Alibaba Group 9 1 0 2 r a M 9 2 ] V C . s c [ 1 v 9 2 5 2 1 . 3 0 9 1 : v i X r a cskaizhang@gmail.com, wmzuo@hit.edu.cn, cslzhang@comp.polyu.edu.hk https://github.com/cszn/DPSR Abstract While deep neural networks (DNN) based single image super-resolution (SISR) methods are rapidly gaining popu- larity, they are mainly designed for the widely-used bicubic degradation, and there still remains the fundamental chal- lenge for them to super-resolve low-resolution (LR) image with arbitrary blur kernels. In the meanwhile, plug-and- play image restoration has been recognized with high ﬂex- ibility due to its modular structure for easy plug-in of de- noiser priors. In this paper, we propose a principled for- mulation and framework by extending bicubic degradation based deep SISR with the help of plug-and-play framework to handle LR images with arbitrary blur kernels. Specif- ically, we design a new SISR degradation model so as to take advantage of existing blind deblurring methods for blur kernel estimation. To optimize the new degradation induced energy function, we then derive a plug-and-play algorithm via variable splitting technique, which allows us to plug any super-resolver prior rather than the denoiser prior as a modular part. Quantitative and qualitative evaluations on synthetic and real LR images demonstrate that the proposed deep plug-and-play super-resolution framework is ﬂexible and effective to deal with blurry LR images. 1. Introduction Single image super-resolution (SISR), with the goal of estimating the clean high-resolution (HR) counterpart x of a given low-resolution (LR) image y, is a classical prob- lem with highly academic and practical values [3]. Basi- cally, the relationship between LR and HR images is char- acterized by the degradation model which deﬁnes how the LR image is degraded from an HR image. Empirical and theoretical studies have proven that an accurate degradation model is crucial for the success of SISR [20, 60]. Thus, it is important to ﬁrst review the degradation model for SISR. ∗Corresponding author. In fact, most existing SISR methods are designed under the assumption of certain degradation model. There are two widely-used degradation models. The ﬁrst one, which is acknowledged as a general degradation model for SISR, is given by y = (x ⊗ k) ↓s + n, (1) where x ⊗ k represents the convolution between blur ker- nel k and HR image x, ↓s is a subsequent downsampling operation with scale factor s, and n is additive white Gaus- sian noise (AWGN) with noise level σ. Such degradation model has been extensively studied on developing model- based optimization methods [13, 19]. However, these meth- ods mostly assume a priori known blur kernel which in prac- tice is difﬁcult to estimate. Although several works such as [41, 53] focus on estimating blur kernel, their source codes are unfortunately not publicly available. The second and perhaps the most widely-used one which we refer to as bicubic degradation is formalized as y = x ↓s . (2) Here, unless otherwise speciﬁed, ↓s instead represents the bicubic downsampler (Matlab default function imresize) with scale factor s. Due to its simplicity, bicubic degra- dation model has become the benchmark setting to eval- uate SISR methods [29, 36]. In particular, it greatly fa- cilities the development of powerful deep neural networks (DNN) for SISR [2]. However, such a simple degradation inevitably gives rise to poor results in many practical sce- narios [20, 65]. Nevertheless, little work has been done on extending to more realistic degradation models. Given the above considerations, it is very necessary to address the following two issues: 1) designing an alterna- tive degradation model, and 2) extending existing DNN- based methods for bicubic degradation to the new degrada- tion model so as to exploit the power of DNN. To this end, we ﬁrst propose a simple yet effective degradation model which assumes the LR image is a bicubicly downsampled, blurred and noisy version of an HR image. Compared to the

general degradation model given by Eqn. (1), the proposed one offers two favorable merits. First, it generalizes the well-studied bicubic degradation model given by Eqn. (2). Second, it enables us to adopt the available blind deblurring methods to estimate the blur kernel from the given LR im- age. In order to extend DNN-based SISR methods to the new degradation model, we propose a well-principled deep plug-and-play super-resolution (DPSR) framework which integrates DNN-based super-resolver into a variable split- ting based iterative optimization scheme. It turns out that the distortion of blur can be effectively handled in Fourier domain. For this reason, it is possible to deal with arbi- trary blur kernels, which is one of the main goals in this pa- per. Moreover, different from existing plug-and-play frame- work [13] which generally plugs the off-the-shelf Gaussian denoiser as a modular part, the proposed instead achieves the plug-in step by applying any existing DNN-based super- resolvers with only a small modiﬁcation. By far, it is worth emphasizing that we mainly focus on non-blind SISR for arbitrary uniform blur kernels rather than blind SISR for arbitrary non-uniform blur kernels. On the one hand, non-blind SISR is important to blind SISR which generally involves alternatively updating the blur kernel and applying non-blind SISR to update the super- resolved image. While some recent works attempt to train DNN to directly estimate the clean image for blind deblur- ring, their practicability needs further evaluations. On the other hand, although the non-uniform blur kernel tends to be a more realistic assumption, it is too complex and still remains to be a difﬁcult problem for image deblurring [31]. In fact, the arbitrary uniform blur kernel assumption is al- ready a much better choice than the simple bicubic kernel for practical applications. Brieﬂy speaking, our work makes a valuable intermediate step from existing bicubic degrada- tion based SISR to ultimate blind SISR. The contribution of this work is summarized as follows: • A more realistic degradation model than bicubic degra- dation model for SISR is proposed. It considers arbi- trary blur kernels and enables to use existing deblur- ring methods for blur kernel estimation. • A deep plug-and-play super-resolution framework is proposed to solve SISR with the new degradation model. DPSR is applicable beyond bicubic degrada- tion and can handle LR images with arbitrary blur ker- nels. • The proposed DPSR is well-principled as the iterative scheme aims to solve the new degradation induced en- ergy function. • The proposed DPSR extends existing plug-and-play framework, showing that the plug-and-play prior for SISR is not limited to Gaussian denoiser. 2. Related work 2.1. DNN-based SISR 1) Bicubic degradation. The ﬁrst DNN-based SISR method, termed as SRCNN [17], employs a relatively shal- low network and follows the previous SISR methods such as A+ [55] and ScSR [61] to synthesize LR images with bicubic interpolation. Since then, by ﬁxing the degradation model to bicubic degradation, some researchers began to improve SISR performance via DNN from different aspects, including PSNR and SSIM values, efﬁciency, and percep- tual visual quality at a large scale factor. To improve the SISR performance in terms of PSNR and SSIM, the very deep super-resolution (VDSR) network pro- posed by Kim et al. [29] shows that the most direct way is to increase the network depth. However, VDSR operates on the bicubicly interpolated LR images which hinders the efﬁ- ciency. To that end, the FSRCNN [18] and ESPCN [50] are proposed to directly manipulate the LR input and adopt an upscaling operation at the end of the network. Considering the fact that the visual results tend to be oversmoothed at a large scale factor (e.g., 4), VGG [52] loss and generative adversarial network (GAN) [24] loss are utilized to improve the perceptual visual quality in [34, 49, 58]. In [20], While achieving great success on bicubic degrada- tion [36, 44, 68], these methods perform poorly on most of real images due to the mismatch of degradation models. 2) Beyond bicubic degradation. the authors pointed out that an accurate estimate of the blur kernel is more important than sophisticated image prior. Since then, several attempts have been made to tackle with LR images beyond bicubic degradation. Zhang et al. [63] proposed a plug-and-play framework (IRCNN) to solve the energy function induced by Eqn. (1). Although in theory IRCNN can handle arbitrary blur kernel (please refer to [13]), the blur kernel of such degradation model in practice is difﬁcult to estimate. Zhang et al. [65] proposed a general DNN- based solution (SRMD) which takes two key degradation parameters as input. However, SRMD only considers the Gaussian blur kernels. In [51], the authors proposed a zero- shot super-resolution (ZSSR) method which trains image- speciﬁc DNN on the testing LR image and can also take the degradation parameters, such as the estimated blur kernel, to improve the performance. While showing impressive re- sults for LR image with internal repetitive structures, ZSSR is less effective for severely blurred LR image. As discussed, the above methods have two main draw- backs. First, they have difﬁculty in blur kernel estimation. Second, they are generally designed for Gaussian-like blur kernel and thus cannot effectively handle severely blurred LR image. It should be noted that a deep blind SISR method for motion blur is proposed in [66]. However, it has limited ability to handle the distortion of arbitrary blur kernels. 2

2.2. Plug-and-play image restoration The plug-and-play image restoration which was ﬁrst in- troduced in [15, 57, 69] has attracted signiﬁcant attentions due to its ﬂexibility and effectiveness in handling various inverse problems. Its main idea is to unroll the energy func- tion by variable splitting technique and replace the prior associated subproblem by any off-the-shelf Gaussian de- noiser. Different from traditional image restoration methods which employ hand-crafted image priors, it can implicitly deﬁne the plug-and-play prior by the denoiser. Remarkably, the denoiser can be learned by DNN with large capability which would give rise to promising performance. During the past few years, a ﬂurry of plug-and-play works have been developed from the following aspects: 1) different variable splitting algorithms, such as half- quadratic splitting (HQS) algorithm [1], alternating di- rection method of multipliers (ADMM) algorithm [8], FISTA [4], and primal-dual algorithm [11, 42]; 2) different applications, such as Poisson denoising [47], demosaick- ing [26], deblurring [56], super-resolution [9, 13, 28, 63], and inpainting [40]; 3) different types of denoiser priors, such as BM3D [14, 21], DNN-based denoisers [6, 62] and their combinations [25]; and 4) theoretical analysis on the convergence from the aspect of ﬁxed point [13, 37, 38] and Nash equilibrium [10, 16, 45]. To the best of our knowledge, existing plug-and-play im- age restoration methods mostly treat the Gaussian denoiser as the prior. We will show that, for the application of plug- and-play SISR, the prior is not limited to Gaussian denoiser. Instead, a simple super-resolver prior can be employed to solve a much more complex SISR problem. 3. Method 3.1. New degradation model In order to ease the blur kernel estimation, we propose the following degradation model y = (x↓s) ⊗ k + n, (3) where ↓s is the bicubic downsampler with scale factor s. Simply speaking, Eqn. (3) conveys that the LR image y is a bicubicly downsampled, blurred and noisy version of a clean HR image x. Since existing methods widely use bicubic downsampler to synthesize or augment LR image, it is a reasonable as- sumption that bicubicly downsampled HR image (i.e., x↓s) is also a clean image. Following this assumption, Eqn. (3) actually corresponds to a deblurring problem followed by a SISR problem with bicubic degradation. Thus, we can fully employ existing well-studied deblurring methods to estimate k. Clearly, this is a distinctive advantage over the degradation model given by Eqn. (1). 3 Once the degradation model is deﬁned, the next step is to formulate the energy function. According to Maximum A Posteriori (MAP) probability, the energy function is for- mally given by 1 min x 2σ2y − (x↓s) ⊗ k2 + λΦ(x), (4) 2σ2y− (x↓s)⊗ k2 is the data ﬁdelity (likelihood) where 1 term1 determined by the degradation model of Eqn. (3), Φ(x) is the regularization (prior) term, and λ is the reg- ularization parameter. For discriminative learning meth- ods, their inference models actually correspond to an energy function where the degradation model is implicitly deﬁned by the training LR and HR pairs. This explains why existing DNN-based SISR methods trained on bicubic degradation perform poorly for real images. 3.2. Deep plug-and-play SISR To solve Eqn. (4), we ﬁrst adopt the variable splitting technique to introduce an auxiliary variable z, leading to the following equivalent constrained optimization formulation: ˆx = arg min x 1 2σ2y − z ⊗ k2 + λΦ(x), subject to z = x↓s . (5) We then address Eqn. (5) with half quadratic splitting (HQS) algorithm. Note that other algorithms such as ADMM can also be exploited. We use HQS for its sim- plicity. 1 2σ2y−z⊗k2+λΦ(x)+ Typically, HQS tackles with Eqn. (5) by minimizing the following problem which involves an additional quadratic penalty term Lµ(x, z) = z−x↓s2, (6) where µ is the penalty parameter, and a very large µ will enforce z approximately equals to x↓s. Usually, µ varies in a non-descending order during the following iterative solu- tion to Eqn. (6) zk+1 = arg min zy − z⊗k2 + µσ2z − xk ↓s2, (7) µ 2 xk+1 = arg min x zk+1 − x↓s2 + λΦ(x). (8) µ 2 It can be seen that Eqn. (7) and Eqn. (8) are alternating min- imization problems with respect to z and x, respectively. In particular, by assuming the convolution is carried out with circular boundary conditions, Eqn. (7) has a fast closed- form solution F(k)F(y) + µσ2F(xk ↓s) zk+1 = F−1 , (9) F(k)F(k) + µσ2 1In order to facilitate and clarify the parameter setting, we empha- size that, from the Bayesian viewpoint, the data ﬁdelity term should be 2σ2 y − (x↓s) ⊗ k2 rather than 1 2y − (x↓s) ⊗ k2. 1

where F(·) and F−1(·) denote the Fast Fourier Transform (FFT) and inverse FFT, F(·) denotes complex conjugate of F(·). To analyze Eqn. (8) from a Bayesian perspective, we rewrite it as follows 2(1/µ)2 1 xk+1 = arg min x zk+1 − x↓s2 + λΦ(x). (10) Clearly, Eqn. (10) corresponds to super-resolving zk+1 with a scale factor s by assuming zk+1 is bicubicly downsam- pled from an HR image x, and then corrupted by AWGN with noise level1/µ. From another viewpoint, Eqn. (10) solves a super-resolution problem with the following simple bicubic degradation model y = x↓s + n. (11) As a result, one can plug DNN-based super-resolver trained on the widely-used bicubic degradation with certain noise levels to replace Eqn. (10). For brevity, Eqn. (8) and Eqn. (10) can be further rewritten as xk+1 = SR(zk+1, s,1/µ). (12) Since the prior term Φ(x) is implicitly deﬁned in SR(·), we refer to it as super-resolver prior. So far, we have seen that the two sub-problems given by Eqn. (7) and Eqn. (8) are relatively easy to solve. In fact, they also have clear interpretation. On the one hand, since the blur kernel k is only involved in the closed-form solution, Eqn. (7) addresses the distortion of blur. In other words, it pulls the current estimation to a less blurry one. On the other hand, Eqn. (8) maps the less blurry image to a more clean HR image. After several alternating iterations, it is expected that the ﬁnal reconstructed HR image contains no blur and noise. 3.3. Deep super-resolver prior In order to take advantage of the merits of DNN, we need to specify the super-resolver network which should take the noise level as input according to Eqn. (12). Inspired by [23, 64], we only need to modify most of the existing DNN-based super-resolvers by taking an additional noise level map as input. Alternatively, one can directly adopt SRMD as the super-resolver prior because its input already contains the noise level map. Since SRResNet [34] is a well-known DNN-based super- resolver, in this paper we propose a modiﬁed SRResNet, namely SRResNet+, to plug in the proposed DPSR frame- work. SRResNet+ differs from SRResNet in several as- pects. First, SRResNet+ additionally takes a noise level map M as input. Second, SRResNet+ increases the number of feature maps from 64 to 96. Third, SRResNet+ removes the batch normalization layer [27] as suggested in [58]. 4 Before training a separate SRResNet+ model for each scale factor, we need to synthesize the LR image and its noise level map from a given HR image. According to the degradation model given by Eqn. (11), the LR image is bicubicly downsampled from an HR image, and then cor- rupted by AWGN with a noise level σ from predeﬁned noise level range. For the corresponding noise level map, it has the same spatial size of LR image and all the elements are σ. Following [65], we set the noise level range to [0, 50]. For the HR images, we choose the 800 training images from DIV2K dataset [2]. We adopt Adam algorithm [30] to optimize SRResNet+ by minimizing the 1 loss function. The leaning rate starts from 10−4, then decreases by half every 5 × 105 iterations and ﬁnally ends once it is smaller than 10−7. The mini- batch size is set to 16. The patch size of LR input is set to 48×48. The rotation and ﬂip based data augmentation is performed during training. We train the models with Py- Torch on a single GTX 1080 Ti GPU. Since this work mainly focuses on SISR with arbitrary blur kernels. We omit the comparison between SRResNet+ and other methods on bicubic degradation. As a simple comparison, SRResNet+ can outperform SRResNet [34] by an average PSNR gain of 0.15dB on Set5 [5]. 3.4. Comparison with related methods In this section, we emphasize the fundamental differ- ences between the proposed DPSR and several closely re- lated DNN-based methods. 1) Cascaded deblurring and SISR. To super-resolve LR image with arbitrary blur kernels, a heuristic method is to perform deblurring ﬁrst and then super-resolve the de- blurred LR image. However, such a cascaded two-step method suffers from the drawback that the perturbation er- ror of the ﬁrst step would be ampliﬁed at the second step. On the contrary, DPSR optimizes the energy function given by Eqn. (4) in an iterative manner. Thus, DPSR tends to deliver better performance. 2) Fine-tuned SISR model with more training data. Per- haps the most straightforward way is to ﬁne-tune existing bicubic degradation based SISR models with more train- ing data generated by the new degradation model (i.e., Eqn. (3)), resulting in the so-called blind SISR. However, the performance of such methods deteriorates seriously es- pecially when large complex blur kernels are considered, possibly because the distortion of blur would further aggra- vate the pixel-wise average problem [34]. As for DPSR, it takes the blur kernel as input and can effectively handle the distortion of blur via Eqn. (9). 3) Extended SRMD or DPSR with end-to-end training. Inspired by SRMD [65], one may attempt to extend it by considering arbitrary blur kernels. However, it is difﬁcult to

sample enough blur kernels to cover the large kernel space. In addition, it would require a large amount of time to train a reliable model. By contrast, DPSR only needs to train the models on the bicubic degradation, thus it involves much less training time. Furthermore, while SRMD can effec- tively handle the simple Gaussian kernels of size 15 × 15 with many successive convolutional layers, it loses effec- tiveness to deal with large complex blur kernels. Instead, DPSR adopts a more concise and specialized modular by FFT via Eqn. (9) to eliminate the distortion of blur. Alter- natively, one may take advantage of the structure beneﬁts of DPSR and resort to jointly training DPSR in an end-to-end manner. However, we leave this to our future work. From the above discussions, we can conclude that our DPSR is well-principled, structurally simple, highly inter- pretable and involves less training. 4. Experiments 4.1. Synthetic LR images Following the common setting in most of image restora- tion literature, we use synthetic data with ground-truth to quantitatively analyze the proposed DPSR, as well as mak- ing a relatively fair comparison with other competing meth- ods. Blur kernel. For the sake of thoroughly evaluating the ef- fectiveness of the proposed DPSR for arbitrary blur kernels, we consider three types of widely-used blur kernels, includ- ing Gaussian blur kernels, motion blur kernels, and disk (out-of-focus) blur kernels [12, 59]. The speciﬁcations of the blur kernels are given in Table 1. Some kernel exam- ples are shown in Fig. 1. Note that the kernel sizes range from 5×5 to 35×35. As shown in Table 2, we further con- sider Gaussian noise with two different noise levels, i.e., 2.55 (1%) and 7.65 (3%), for scale factor 3. Table 1. Three different types of blur kernels. Type Gaussian # 16 Motion 32 Disk 8 Speciﬁcation 8 isotropic Gaussian kernels with standard devi- ations uniformly sampled from the interval [0.6, 2], and 8 selected anisotropic Gaussian blur ker- nels from [65]. 8 blur kernels from [35] and their augmented 8 kernels by random rotation and ﬂip; and 16 realistic-looking motion blur kernels generated by the released code of [7]. 8 disk kernels with radius uniformly sampled from the interval [1.8, 6]. They are generated by matlab function fspecial(’disk’,r), where r is the radius. (a) Gaussian (b) Motion (c) Disk Fig. 1. Examples of (a) Gaussian blur kernels, (b) motion blur ker- nels and (c) disk blur kernels. 5 Parameter setting. In the alternating iterations between Eqn. (7) and Eqn. (8), we need to set λ and tune µ to ob- tain a satisfying performance. Setting such parameters has been considered as a non-trivial task [46]. However, the parameter setting of DPSR is generally easy with the fol- √ lowing two principles. First, since λ is ﬁxed and can be absorbed into σ, we can instead multiply σ by a scalar λ and therefore ignore the λ in Eqn. (8). Second, since µ has a non-descending order during iterations, we can instead set the1/µ from Eqn. (12) with a non-ascending order crease1/µ from 49 to a small σ-dependent value (e.g., to indirectly determine µ in each iteration. Empirically, a good rule of thumb is to set λ to 1/3 and exponentially de- max(2.55, σ)) for a total of 15 iterations. Compared methods. We compare the proposed DPSR with six methods, including two representative DNN-based methods for bicubic degradation (i.e., VDSR [29] and RCAN [67]), two cascaded deblurring and SISR meth- ods (i.e., IRCNN+RCAN and DeblurGAN+RCAN), and two specially designed methods for blurry LR images (i.e., GFN [66] and ZSSR [51]). To be speciﬁc, VDSR is the ﬁrst very deep network for SISR; RCAN consists of more than 400 layers and achieves state-of-the-art perfor- mance for bicubic degradation; IRCNN is a plug-and-play method with deep denoiser prior that can handle non-blind image deblurring; DeblurGAN [32] is a deep blind de- blurring method based on generative adversarial network (GAN) [24]; GFN is a DNN-based method for joint blind motion deblurring and super-resolution; ZSSR is an unsu- pervised DNN-based method that can super-resolve blurry and noisy LR images. Note that IRCNN, ZSSR and DPSR can take the blur kernel and noise level as input. For a fair comparison, we modify ZSSR to our new degradation model. Quantitative results. The PSNR and SSIM results of dif- ferent methods for different degradation settings on the color BSD68 dataset [39, 48, 62] are shown in Table 2, from which we have several observations. First, while RCAN outperforms VDSR by a large margin for bicubic degrada- tion (see [67]), it has comparable performance to VDSR and even bicubic interpolation for the complex degrada- tions settings. Such phenomenon has also been reported in [51, 65]. Second, after a deblurring step by IRCNN, IRCNN+RCAN can signiﬁcantly improve the PSNR and SSIM values. Third, DeblurGAN+RCAN and GFN give rise to poor performance which may be attributed to the limited capability of successive convolutional layers in han- dling distortion of large complex blur. Fourth, ZSSR is less effective for large complex blur kernels due to the lack of re- currence property of the blurry LR image. Last, our DPSR achieves the best performance since it directly optimizes the energy function for the given degradation and can ef- fectively handle the distortion of blur via Eqn. (9).

Table 2. Average PSNR and SSIM results of different methods for different degradation settings on the color BSD68 dataset [39, 48, 62]. The best two results are highlighted in red and blue colors, respectively. Degradation Setting Scale Factor ×2 Kernel Type Gaussian Motion Disk Gaussian Motion Disk Gaussian Motion Disk Gaussian Motion Disk Gaussian Motion Disk ×3 ×4 Noise Level 0 0 2.55 (1%) 7.65 (3%) 0 Bicubic VDSR RCAN 23.47/0.596 19.84/0.449 21.85/0.507 22.11/0.526 18.83/0.424 20.70/0.464 22.05/0.513 18.80/0.412 20.65/0.452 21.60/0.436 18.58/0.346 20.32/0.380 21.18/0.486 18.10/0.407 19.86/0.439 23.36/0.589 19.86/.451 21.86/0.508 22.03/0.520 18.84/0.424 20.70/0.465 21.95/0.507 18.81/0.413 20.66/0.453 21.54/0.433 18.60/0.350 20.34/0.384 21.11/0.482 18.11/0.408 19.86/0.440 23.59/0.603 19.82/0.448 21.85/0.507 22.20/0.532 18.81/0.422 20.69/0.464 22.05/0.495 18.74/0.390 20.59/0.429 21.01/0.342 18.21/0.259 19.81/0.288 21.27/0.491 18.08/0.406 19.85/0.439 Methods IRCNN +RCAN 24.79/0.629 28.54/0.806 25.48/0.671 23.52/0.566 25.88/0.699 23.82/0.594 22.95/0.540 24.18/0.604 22.33/0.517 22.07/0.463 22.47/0.514 21.19/0.483 22.61/0.526 24.42/0.625 22.72/0.540 DeblurGAN +RCAN 19.36/0.400 17.46/0.268 19.33/0.370 18.18/0.347 16.25/0.228 18.28/0.336 17.64/0.195 15.55/0.122 16.74/0.142 14.93/0.094 13.91/0.065 14.43/0.071 17.52/0.329 15.68/0.225 17.59/0.321 GFN ZSSR DPSR – – – – – – – – – – – – 21.66/0.507 17.79/0.398 20.38/0.460 21.44/0.542 17.99/0.367 21.25/0.490 18.97/0.442 16.80/0.348 19.05/0.430 20.52/0.477 18.19/0.402 19.88/0.441 20.22/0.407 18.07/0.340 19.64/0.373 16.83/0.380 15.58/0.329 16.91/0.392 27.28/0.763 30.05/0.869 28.61/0.816 25.22/0.665 27.22/0.769 26.19/0.716 23.92/0.595 24.94/0.648 23.44/0.567 23.17/0.557 23.28/0.564 22.25/0.515 24.04/0.604 25.69/0.695 24.84/0.649 PSNR/SSIM (a) Ground-truth ×4 (b) LR (17.25/0.406) (c) Bicubic (17.12/0.397) (d) VDSR (17.37/0.416) (e) RCAN (18.28/0.472) (f) IRCNN+RCAN (15.29/0.227) (g) DeblurGAN+RCAN (17.58/0.437) (h) GFN (16.61/0.374) (i) ZSSR (19.44/0.577) (j) DPSR(ours) Fig. 2. The performance comparison of different methods for scale factor 4 on image “253027” with Gaussian kernel. The blur kernel is shown on the upper-left corner of the LR image. 17.87/0.510 23.13/0.693 15.44/0.280 17.43/0.493 17.27/0.474 23.75/0.739 22.66/0.640 (a) RCAN 28.53/0.704 22.58/0.571 (b) IRCNN+RCAN (c) DeblurGAN+RCAN 23.93/0.677 (d) GFN 15.41/0.549 (e) ZSSR 31.35/0.798 (f) DPSR(ours) Fig. 3. The performance comparison of different methods for scale factor 4 on image “102061” with motion kernel (ﬁrst row) and image “189080” with disk kernel (second row). The blur kernel is shown on the upper-left corner of the super-resolved image by RCAN. 6

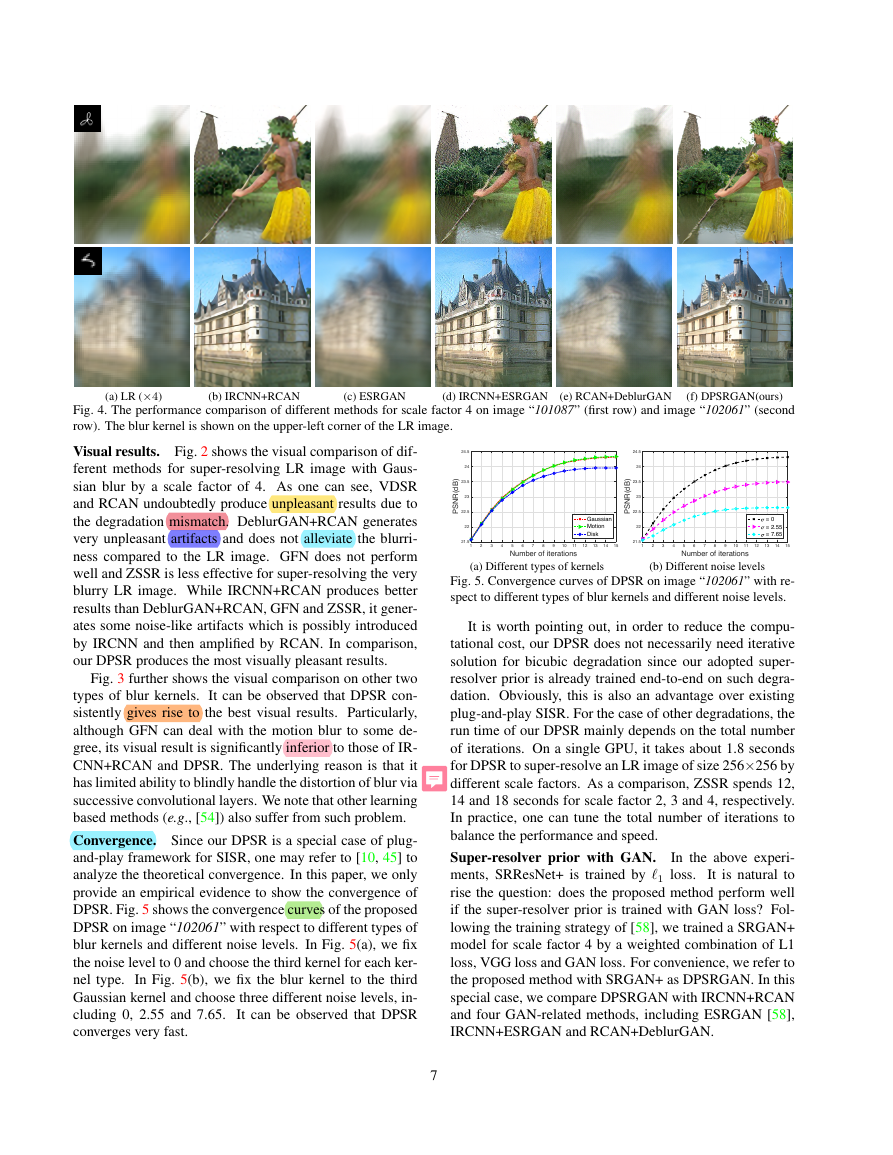
(a) LR (×4) (b) IRCNN+RCAN (c) ESRGAN (d) IRCNN+ESRGAN (e) RCAN+DeblurGAN (f) DPSRGAN(ours) Fig. 4. The performance comparison of different methods for scale factor 4 on image “101087” (ﬁrst row) and image “102061” (second row). The blur kernel is shown on the upper-left corner of the LR image. Visual results. Fig. 2 shows the visual comparison of dif- ferent methods for super-resolving LR image with Gaus- sian blur by a scale factor of 4. As one can see, VDSR and RCAN undoubtedly produce unpleasant results due to the degradation mismatch. DeblurGAN+RCAN generates very unpleasant artifacts and does not alleviate the blurri- ness compared to the LR image. GFN does not perform well and ZSSR is less effective for super-resolving the very blurry LR image. While IRCNN+RCAN produces better results than DeblurGAN+RCAN, GFN and ZSSR, it gener- ates some noise-like artifacts which is possibly introduced by IRCNN and then ampliﬁed by RCAN. In comparison, our DPSR produces the most visually pleasant results. Fig. 5. Convergence curves of DPSR on image “102061” with re- spect to different types of blur kernels and different noise levels. (a) Different types of kernels (b) Different noise levels Fig. 3 further shows the visual comparison on other two types of blur kernels. It can be observed that DPSR con- sistently gives rise to the best visual results. Particularly, although GFN can deal with the motion blur to some de- gree, its visual result is signiﬁcantly inferior to those of IR- CNN+RCAN and DPSR. The underlying reason is that it has limited ability to blindly handle the distortion of blur via successive convolutional layers. We note that other learning based methods (e.g., [54]) also suffer from such problem. Convergence. Since our DPSR is a special case of plug- and-play framework for SISR, one may refer to [10, 45] to analyze the theoretical convergence. In this paper, we only provide an empirical evidence to show the convergence of DPSR. Fig. 5 shows the convergence curves of the proposed DPSR on image “102061” with respect to different types of blur kernels and different noise levels. In Fig. 5(a), we ﬁx the noise level to 0 and choose the third kernel for each ker- nel type. In Fig. 5(b), we ﬁx the blur kernel to the third Gaussian kernel and choose three different noise levels, in- cluding 0, 2.55 and 7.65. It can be observed that DPSR converges very fast. 7 It is worth pointing out, in order to reduce the compu- tational cost, our DPSR does not necessarily need iterative solution for bicubic degradation since our adopted super- resolver prior is already trained end-to-end on such degra- dation. Obviously, this is also an advantage over existing plug-and-play SISR. For the case of other degradations, the run time of our DPSR mainly depends on the total number of iterations. On a single GPU, it takes about 1.8 seconds for DPSR to super-resolve an LR image of size 256×256 by different scale factors. As a comparison, ZSSR spends 12, 14 and 18 seconds for scale factor 2, 3 and 4, respectively. In practice, one can tune the total number of iterations to balance the performance and speed. Super-resolver prior with GAN. In the above experi- ments, SRResNet+ is trained by 1 loss. It is natural to rise the question: does the proposed method perform well if the super-resolver prior is trained with GAN loss? Fol- lowing the training strategy of [58], we trained a SRGAN+ model for scale factor 4 by a weighted combination of L1 loss, VGG loss and GAN loss. For convenience, we refer to the proposed method with SRGAN+ as DPSRGAN. In this special case, we compare DPSRGAN with IRCNN+RCAN and four GAN-related methods, including ESRGAN [58], IRCNN+ESRGAN and RCAN+DeblurGAN. 123456789101112131415Number of iterations21.52222.52323.52424.5PSNR(dB)GaussianMotionDisk123456789101112131415Number of iterations21.52222.52323.52424.5PSNR(dB) = 0 = 2.55 = 7.65

(a) LR (d) ZSSR (e) DPSR(ours) Fig. 6. The visual comparison of different methods on “chip” with scale factor 4 (ﬁrst row), “frog” with scale factor 3 (second row) and “colour” with scale factor 2 (third row). The estimated blur kernel is shown on the upper-left corner of the LR image. Note that we assume the noisy image “frog” has no blur. (b) RCAN (c) SRMD Fig. 4 shows the visual comparison of different methods. It can be seen that directly super-resolving the blurry LR image by ESRGAN does not improve the visual quality. By contrast, IRCNN+ESRGAN can deliver much better visual results as the distortion of blur is handled by IRCNN. Mean- while, it ampliﬁes the perturbation error of IRCNN, result- ing in unpleasant visual artifacts. Although DeblurGAN is designed to handle motion blur, RCAN+DeblurGAN does not perform as well as expected. In comparison, our DPSR- GAN produces the most visually pleasant HR images with sharpness and naturalness. 4.2. LR images with estimated kernel In this section, we focus on experiments on blurry LR images with estimated blur kernel. Such experiments can help to evaluate the feasibility of the new degradation model, the practicability and kernel sensitivity of the pro- posed DPSR. It is especially noteworthy that we do not know the HR ground-truth of the LR images. Fig. 6 shows the visual comparison with state-of-the- art SISR methods (i.e., RCAN [67], SRMD [63] and ZSSR [51]) on classical image “chip” [22], noisy image “frog” [33] and blurry image “colour” [43]. For the “chip” and “colour”, the blur kernel is estimated by [43]. For the noisy “frog”, we assume it has no blur and directly adopt our super-resolver prior to obtain the HR image. Note that once the blur kernel is estimated, our DPSR can reconstruct HR images with different scale factors, whereas SRMD and ZSSR with Eqn. (1) need to estimate a separate blur kernel for each scale factor. From Fig. 6, we can observe that RCAN has very limited ability to deal with blur and noise because of its oversimpli- ﬁed bicubic degradation model. With a more general degra- dation model, SRMD and ZSSR yield better results than RCAN on “chip” and “frog”. However, they cannot recover the latent HR image for the blurry image “colour” which is blurred by a large complex kernel. In comparison, our DPSR gives rise to the most visually pleasant results. As a result, our new degradation model is a feasible assumption and DPSR is an attractive SISR method as it can handle a wide variety of degradations. 5. Conclusion In this paper, we proposed a well-principled deep plug- and-play super-resolution method for LR image with arbi- trary blur kernels. We ﬁrst design an alternative degradation model which can beneﬁt existing blind deblurring methods for kernel estimation. We then solve the corresponding en- ergy function via half quadratic splitting algorithm so as to exploit the merits of plug-and-play framework. It turns out we can explicitly handled the distortion of blur by a special- ized modular. Such a distinctive merit actually enables the proposed method to deal with arbitrary blur kernels. It also turns out that we can plug super-resolver prior rather than denoiser prior into the plug-and-play framework. As such, we can fully exploit the advances of existing DNN-based SISR methods to design and train the super-resolver prior. Extensive experimental results demonstrated the feasibility of the new degradation model and effectiveness of the pro- posed method for super-resolving LR images with arbitrary blur kernels. 6. Acknowledgements This work is supported by HK RGC General Research Fund (PolyU 152216/18E) and National Natural Science Foundation of China (grant no. 61671182, 61872118, 61672446). 8

分享到：

赞收藏

资料库

Deep Plug-and-Play Super-Resolution for Arbitrary Blur Kernels_注....pdf

相关推荐

人工智能

热门标签

最新资料