科 技 信 息 语音信号共振峰提取方法的研究分析 青海师范大学物理系 杨 丹 姜占才 余蓥良 李振起 ［摘 要］目前的提取语音共振峰的方法比较多，常用的方法有倒谱法、LPC 谱估计法、LPC 倒谱法，但没有一种方法是十分完美的，为 了系统的深入的研究共振峰的提取，本文对同一帧语音信号进行了不同方法的共振峰提取实验仿真，给出了具体的共振峰频率数 据，同时对不同方法的优缺点进行了科学的、深入的研究分析，用 Matlab 对算法进行仿真实现，实验结果表明共振峰的提取方案中 LPCC 倒谱法避免了一般同态处理中对复对数的麻烦，可以较为理想的实现对共振峰的提取。 ［关键词］共振峰 倒谱法 LPC 谱估计法 LPC 倒谱法 同态处理 0.引言 在语音数字信号处理的研究中，语音信号的共振峰是一个十分重 要的性能参数。共振峰是准周期脉冲激励进入声道时产生的一组共振 频率。共振峰参数包括共振峰频率和频带宽度，它是区别不同韵母的 重要参数。当前共振峰的提取方法有很多种，每种方法各有利弊，本文 对多种共振峰提取方法进行实验和比较分析。 与基音提取类似，得到精确的共振峰估值也是很困难的，这些困难是： （1）虚假峰值 在正常情况下，频谱包络中的最大值完全是由共振峰引起的。但 有时会出现虚假峰值，在利用非线性预测分析方法的频谱包络估计时， 出现虚假峰值情况较多，而采用线性预测方法时，出现虚假峰值情况得 到了很大的改善。 （2）共振峰合并 当出现相邻共振峰时，可能会有频率靠得太近难以分辨的情况，而 寻找一种理想的能对共振峰合并进行识别的共振峰提取算法有不少实 际困难。 （3）高音调语音 传统的频谱包络估值方法是利用由谐波峰值提供的样点，而高音 调语音（如女声和童声）的谐波间隔比较宽，因而为频谱包络估值所提 供的样点比较少。而利用线性预测进行频谱包络估值可以一定程度上 改善这一问题。 1.谱包络提取 共振峰信息包含在语音频谱包络中，因此共振峰参数提取的关键 是估计自然语音频谱包络，并认为谱包络中的最大值就是共振峰。下 图 1 是对 21 帧信号的线性预测谱包络提取分析。 2.倒谱法提取共振峰 虽然可以直接对语音信号求离散傅里叶变换（DFT），然后用 DFT 谱来提取语音信号的共振峰参数，但是，直接 DFT 的谱要受基频谐波的 影响，最大值只能出现在谐波频率上，因而共振峰测定误差较大。为了 消除基频谐波的影响，可以采用同态解卷技术，经过同态滤波后得到平 滑的谱，这样简单地检测峰值就可以直接提取共振峰参数，因而这种方 法更为有效和精确。因为倒谱运用对数运算和二次变换将基音谐波和 声道的频谱包络分离开来。因此用低时窗 l(n)从语音信号倒谱 c(n)中所 截取出来得 h(n)，能更精确地反映声道响应。这样，由 h(n)经 DFT 得到 的 Ĥ (k) ，就是声道的离散谱曲线，用 Ĥ (k) 代替直接 DFT 的频谱，因为 去除了激励引起的谐波波动，所以可以更精确地得到共振峰参数。 图 2 倒谱法求取的共振峰参数图 3.LPC 法提取共振峰 从线性预测导出的声道滤波器是频谱包络估计器的最新形式，线 性预测提供了一个优良的声道模型（条件是语音不含噪声）。尽管线性 预测法的频率灵敏度和人耳不相匹配，但它仍是最廉价、最优良的行之 有效的方法。 用线性预测可对语音信号进行解卷：即把激励分量归入预测残差 中，得到声道响应的全级模型 H(z)的分量，从而得到这个分量的 ai 参 数。尽管其精度由于存在一定的逼近误差而有所降低，但去除了激励 分量的影响。此时求出声道响应分量的谱峰，就可以求出共振峰，这里 有两种途径：一是用标准的求取复根的方法计算全级模型分母多项式 A(z)的根，称为求根法；一是用运算量较少的 DFT 法，求 A(z)的离散频率 响应 A(k)的谷点来得到共振峰的位置。因为 A(z) = 1 - ∑ z-i ，所以 若求此多项式系数序列（1，a1，a2，…，ap）的 DFT，就可以得到 A(k)。但是 一般预测阶数 p 不大，这就影响了求其谷点即求其共振峰频率值的精 度。为了提高 DFT 的频率分辨率，可以采用补 0 的办法增加序列的时 间长度，即用（1，a1，a2，…，ap，0,0，…，0）进行 DFT，为了能利用 FFT，长度 一般取为 64 点、128 点、256 点、512 点等。另外也可以采用抛物线内插 技术，解决频率分辨率较低的情况下的共振峰频率值的求取。 ai p i = 1 图 1 图 3 LPC 谱估计法求取的共振峰参数图 161 — — 

科 技 信 息 4.求根法提取共振峰 找出多项式复根的过程通常采用牛顿—拉夫逊（Newton-Raphson） 算法。其方法是一开始先猜测一个根值并就此猜测值计算多项式及其 导数的值，然后利用结果再找出一个改进的猜测值。当前后两个猜测 值之差小于某门限时结束猜测过程。由上述过程可知，重复运算找出 复根的计算量相当可观。然而，假设每一帧的最初猜测值域前一帧的 根的位置重合，那么根的帧到帧的移动足够小，经过较少的重复运算 后，可使新的根的值会聚在一起。当求根过程初始时，第一帧的猜测值 可以在单位圆上等间隔设置。 具体过程是：设：z i = rie-jθi 也是 一个根。设与 i 对应的共振峰频率为 Fi，3dB 带宽为 Bi，则它们存在下面 的关系： i = rie jθi 为第一个根，则其共轭值 z i e-BiπT = ri Bi = -ln ri πT 2πTFi = θ 所以： θ Fi = i 2πT 式中，T 是采样周期。 因为预测器阶数 p 是预先选定的，所以复共轭对的数量最多是 p/2。 因而判断某一个极点属于哪一个共振峰的问题就不太复杂。而且，不 属于共振峰的额外极点容易排除掉，因为其带宽比共振峰带宽要大得 多。 5.LPC 倒谱法提取共振峰 语音信号的倒谱可以通过对信号做傅里叶变换，取模的对数，在求 反傅里叶变换得到。由于频率响应 H(e jω) 反应声道的频率响应和被 分析信号的谱包络，因此用 log |H(e jω)| 做傅里叶反变换求出的 LPC 倒谱 系数，也可以被认为是包含了信号谱的包络信息，因此可以将其看作对 原信号短时倒谱的一种近似。 图 4 LPC 倒谱法求取的共振峰参数图 通 过 线 性 预 测 分 析 得 到 的 合 成 滤 波 器 的 系 统 函 数 为 ，其冲击响应为 h(n)。下面求 h(n)的倒谱 ĥ(n) ，首先 H(z) = 1 1 - ∑ p i = 1 z-i ai 根据同态分析方法，有 Ĥ (z) = log H(z) 因为 H(z)是最小相位的，即在单 位 院 内 是 解 析 的 ，所 以 Ĥ (z) 一 定 可 以 展 开 成 级 数 形 式 ，即 Ĥ (z) = ∑ +∞ ĥ(n)z-n ，就是说 Ĥ (z) 的逆变换 ĥ(n) 是存在的。设 ĥ(0) = 0 ， 将式两边同时对 z-1 求导，得 n = 1 1 1 - ∑ p i = 1 z-i a i ö ÷ ÷ ÷ ÷÷ ÷ ø æ ç ç ç çç ç è ∂ ∂z-1 log 得到 ∂z-i∑ = ∂ n = 1 +∞ ĥ(n)z-n ∑ +∞ nĥ(n)z-n + 1 = n = 1 p ∑ iai 1 - ∑ i = 1 p z-i + 1 z-i ai i = 1 （上接第 165 页） ［1］王宏志.一本《晚清翻译史》的构思［J］.中国比较文学,2001,(2):104. ［2］谭汝谦.中国译日本书综合目录［M］.香港:香港中文大学出版 社,1980. ［3］(日)实藤惠秀.中国人留学日本史［M］.谭汝谦,林启彦译.北京: 生活·读书·新知三联书店,1983. ［4］李 喜 所. 近 代 中 国 的 留 学 生［M］. 北 京: 北 京 人 民 出 版 社 ， ［5］费正清.剑桥中国晚清史下卷［M］.北京:中国社会科学出版社， 1987.122、124、144、198-201. 162 — — 有 æ 1 - ∑ çç è i = 1 p ai z-i ∑ +∞ nĥ(n)z-n + 1 = ∑ +∞ iai ö ÷÷ ø n = 1 n = 1 z-i + 1 ，令式左右两边 z 的各次 幂前系数分别相等得到 1 - i ĥ(1) = a1 ì ï ïï ĥ(n) = an + ∑ n - 1æ n aiĥ( ö ï èç ø÷ í i = 1 ï ïï ĥ(n) = ∑ p æ 1 - i n aiĥ( ö ) ï èç ø÷ î i = 1 按照上式可直接从预测系数{ai}求得倒谱 ĥ(n) 。这个倒谱是根据 1 ≤ n ≤ p n > p n - i n - i ) 现行预测模型得到的，又称为 LPC 倒谱。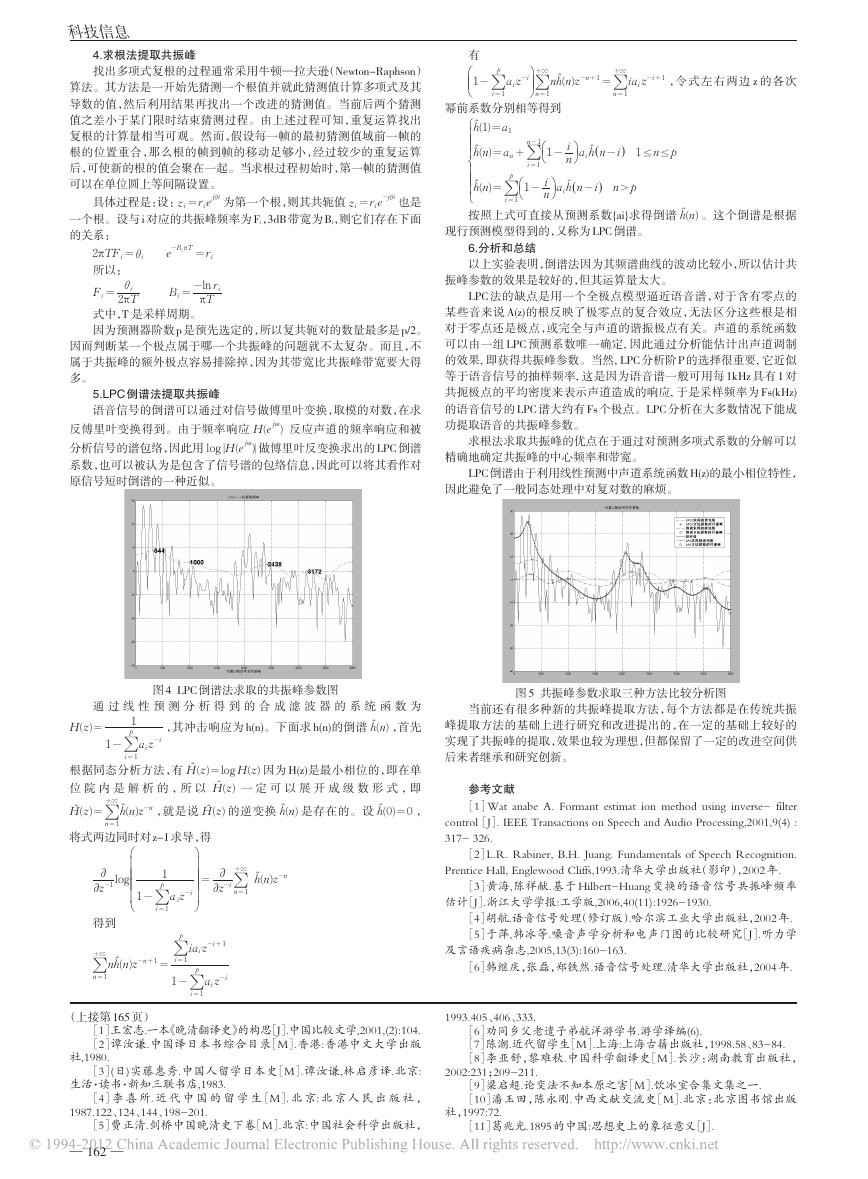 6.分析和总结 以上实验表明，倒谱法因为其频谱曲线的波动比较小，所以估计共 振峰参数的效果是较好的，但其运算量太大。 LPC 法的缺点是用一个全极点模型逼近语音谱，对于含有零点的 某些音来说 A(z)的根反映了极零点的复合效应，无法区分这些根是相 对于零点还是极点，或完全与声道的谐振极点有关。声道的系统函数 可以由一组 LPC 预测系数唯一确定, 因此通过分析能估计出声道调制 的效果, 即获得共振峰参数。当然, LPC 分析阶 P 的选择很重要, 它近似 等于语音信号的抽样频率, 这是因为语音谱一般可用每 1kHz 具有 1 对 共扼极点的平均密度来表示声道造成的响应, 于是采样频率为 Fs(kHz) 的语音信号的 LPC 谱大约有 Fs 个极点。LPC 分析在大多数情况下能成 功提取语音的共振峰参数。 求根法求取共振峰的优点在于通过对预测多项式系数的分解可以 精确地确定共振峰的中心频率和带宽。 LPC 倒谱由于利用线性预测中声道系统函数 H(z)的最小相位特性， 因此避免了一般同态处理中对复对数的麻烦。 图 5 共振峰参数求取三种方法比较分析图 当前还有很多种新的共振峰提取方法，每个方法都是在传统共振 峰提取方法的基础上进行研究和改进提出的，在一定的基础上较好的 实现了共振峰的提取，效果也较为理想，但都保留了一定的改进空间供 后来者继承和研究创新。 参考文献 ［1］Wat anabe A. Formant estimat ion method using inverse- filter control［J］. IEEE Transactions on Speech and Audio Processing,2001,9(4) : 317- 326. ［2］L.R. Rabiner, B.H. Juang. Fundamentals of Speech Recognition. Prentice Hall, Englewood Cliffs,1993.清华大学出版社（影印），2002 年. ［3］黄海,陈祥献.基于 Hilbert-Huang 变换的语音信号共振峰频率 估计［J］.浙江大学学报:工学版,2006,40(11):1926-1930. ［4］胡航.语音信号处理（修订版）.哈尔滨工业大学出版社，2002 年. ［5］于萍,韩冰等.嗓音声学分析和电声门图的比较研究［J］.听力学 及言语疾病杂志,2005,13(3):160-163. ［6］韩继庆，张磊，郑铁然.语音信号处理.清华大学出版社，2004 年. 1993.405、406、333. ［6］劝同乡父老遣子弟航洋游学书.游学译编(6). ［7］陈潮.近代留学生［M］.上海:上海古籍出版社，1998.58、83-84. ［8］李亚舒，黎难秋.中国科学翻译史［M］.长沙：湖南教育出版社， 2002:231；209-211. ［9］梁启超.论变法不知本原之害［M］.饮冰室合集文集之一. ［10］潘玉田，陈永刚.中西文献交流史［M］.北京：北京图书馆出版 社，1997:72. ［11］葛兆光.1895 的中国:思想史上的象征意义［J］.