基于T-S模糊模型的水轮机调节系统辨识.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.29M 资料格式：pdf 举报版权申诉

weixin_38672807-12121284-4744302543305868029.pdf-第1页.png

第1页 / 共7页

weixin_38672807-12121284-4744302543305868029.pdf-第2页.png

第2页 / 共7页

weixin_38672807-12121284-4744302543305868029.pdf-第3页.png

第3页 / 共7页

weixin_38672807-12121284-4744302543305868029.pdf-第4页.png

第4页 / 共7页

weixin_38672807-12121284-4744302543305868029.pdf-第5页.png

第5页 / 共7页

weixin_38672807-12121284-4744302543305868029.pdf-第6页.png

第6页 / 共7页

weixin_38672807-12121284-4744302543305868029.pdf-第7页.png

第7页 / 共7页

文本预览

基于 T-S 模糊模型的水轮机调节系统辨识1 http://www.paper.edu.cn 李超顺，周建中，安学利，向秀桥，李清清，黄志伟华中科技大学水电与数字化工程学院，武汉(430074) E-mail: jz.zhou@hust.edu.cn 摘要：针对水轮机调节系统的复杂性、非线性和难以用明确数学模型表达的特点，建立了该系统的 T-S 模糊模型。考虑到 T-S 模糊模型的结构与参数间的密切关联性，提出基于混沌优化策略的结构和参数一体化辨识。该方法用混沌优化策略辨识模型的前件参数，用最小二乘法辨识模型后件参数，实现了模糊模型结构的自适应优化。以水轮机调节系统频率扰动和负荷扰动实验数据为依据，建立了 T-S 模糊模型并进行了辨识，对辨识的模糊模型进行了频率扰动和负荷扰动仿真实验。对该系统模糊模型辨识及仿真结果表明，本文建立的 T-S 辨识模型具有较高的辨识精度及较强的泛化能力,提出的模型辨识方法有效可行。关键词：水轮机；调速器；T-S 模糊模型；系统辨识；混沌优化；最小二乘法中图分类号：TM6; TP18 0. 引言电网的日益发展对水电机组的控制、故障诊断和安全稳定运行的要求越来越高，为了开展对水电机组的自适应控制、智能故障诊断和系统稳定性计算等方面的研究，建立水轮机调节系统的数学模型有着极其重要的作用。水轮机调节系统是一个复杂的非线性系统，具有时变、非最小相位等特点，对其建立精确的数学模型很困难，为此，学者们对水轮机调节系统进行了系统辨识方面的研究，以期获得系统的模型和参数。水轮机调节系统辨识大概有两种方法：(1) 对呈现复杂非线性的水轮机模型进行线性化处理，设定系统模型结构，通过最小二乘法或人工智能等方法确定系统模型参数[1,2]；(2)利用神经网络的自适应、自学习和非线性逼近能力，对系统进行辨识[3,4]。方法(1)得到的只是系统近似的线性模型，不能完全体现系统的特性。方法(2)中神经网络的局部极小，初值和结构选取等方面的问题没有很好的解决方法。基于模糊规则的模糊辨识为非线性和不确定系统的辨识提供了一种有效方法[5-6]。模糊系统中的 Takagi-Sugeno(T-S)模糊模型[5]由于具有极强的非线性逼近能力，和较少的规则数和简单的结构而受到广泛关注，在复杂系统辨识中应用广泛[7-15]。T-S 模糊模型辨识分为前件参数辨识和后件参数辨识，文献[16]指出，前件参数和后件参数是紧密相关的，对其进行一体辨识能获得更好的性能和精度。混沌优化策略是近年来发展的一种优化思想，该类方法利用混沌变量的随机性、遍历性进行优化搜索，因此具有极强的全局寻优能力，引起了广泛关注。文献[17]指出混沌优化作为一种全局优化方法，寻优效率明显高于其他优化方法如遗传算法和模拟退火算法等。针对水轮机调节系统的辨识中存在的问题与困难，考虑到混沌优化是一种新型的全局快速寻优方法，本文提出了一种基于混沌优化的 T-S 模糊模型一体化辨识方法。该方法用混沌优化策略辨识前件参数，用最小二乘法辨识后件参数，方法具有模糊结构自适应优化能力，因此能得到较高精度的辨识结果。本文建立并研究了水轮机调节系统的 T-S 模糊模型，对该系统的 T-S 模糊模型进行了辨识和仿真，实验结果表明，用本文提出的辨识方法对该模型新型辨识，辨识精度高，泛化能力强。 1本课题得到国家重点基础研究计划(973)课题（2007CB714107）国家自然科学基金（50579022）；高等学校博士学科点专项科研基金资助项目（20050487062）的资助。 - 1 -

http://www.paper.edu.cn 1. T-S 模糊模型及其辨识方法 1.1 T-S 模糊模型设待辨识的系统 P(X,Y)为 MISO 系统， X ∈ 为系统输入， RY ∈ 为系统输出。该系统 mR 模型可以由如下规则表示： 1x is Rule i: IF iA1 and…and mx is y p 0 = i i 其中，i=1,2,..,N，N 为规则数； X = [ mA THEN i xp 1 + +⋅⋅⋅+ i 1 mxxx , , ] 1 2 xp m i （1）为输入数据，m 为输入数据维数； iy 为第 m i 条规则输出， m ip 为模型参数。系统的输出由下式表示： ) y N ∑ i 1 == N ∑ i 1 = yw i w i i （2） m j = w i (μ ，其中， ∏ 函数选用高斯型隶属度函数： A i 1 = ) j j iAμ 为隶属度。这里隶属度 ( ) j =μ A i ) ( exp( − ( x j 2 ) j i c j − r i ) （3） ic 和 j 其中， j 这样，由输入输出数据依据模糊规则 IF-THEN 就可以建立系统的 T-S 模糊模型。 ir 分别为高斯型隶属度函数的中心和宽度。 1.2 混沌优化策略混沌变量具有随机性、遍历性和规律性，利用混沌变量进行优化搜索的基本思想是：用一种混沌映射产生混沌变量，把混沌变量投影到优化变量的取值区间，再用混沌变量进行搜索[17]。混沌变量的随机性和遍历性决定了混沌优化方法快速全局寻优的可能性。混沌变量由 Logistic 映射产生混沌变量： x μ x ) 当 4=μ 时，式(4)处于完全混沌状态。变尺度混沌优化步骤： 1）初始化混沌变量 = 2）粗搜索。将混沌变量初值代入 Logistic 映射，然后进行如下循环：用 Logistic 映射产（4），m 为优化变量维数。 ]}1,0[ xm , i ,..2,1 ]1,0[ =+ 1 x { i 1( ∈ ∈ X = − x x i | 0 0 0 k k k k 生新的混沌变量 ix ，把 ix 投影到优化变量 ip 的取值区间 [ i ba ： ] , i （5）然后将 ip 代入优化目标函数 Jm 计算目标函数值。如果当前 Jm 值优于历史最优值 ∗Jm ， b ( − i xa ) i + = p a i i i 则更新 ∗Jm ， ∗ ip 。如果循环若干步 ∗Jm 保持不变则进入 3）。 3）变尺度搜索。按下式缩小区间 a b i i = = ∗ ∗ p p i i − + [ i , ] i ba ： a ( γ a ( γ − − b b i i i i （6） ) ) - 2 -

其中， )5.0,0(∈γ 。将 Logistic 更新的混沌变量按式（5）投影到优化变量，计算更新最 http://www.paper.edu.cn 优目标函数值 ∗Jm 和最优变量值 ∗ ip 。 1.3 T-S 模糊模型结构确定模型结构即对输入的模糊空间进行划，确定输入量的模糊等级数。在对输入模糊空间进行划分时，模糊等级划分得细能增加模型精度，但会增加计算复杂度，划分得稀能降低计算负担，但会影响模型精度。一般依据具体对象，输入量的模糊等级划分数取 3-10[15]。模糊等级划分的实质是确定式（3）中每个模糊子集对应的隶属度函数的中心和宽度。常用的结构辨识方法有模糊网格法、模糊聚类法等来获得隶属度函数的中心和宽度，本文把高斯型隶属度函数参数的求解看作非线性函数的优化问题，提出用前述混沌优化策略来优化模糊模型结构。利用变尺度混沌优化方法辨识模型结构，混沌优化的目标函数如下式： J = L ∑ k 1 = (1 L y k − ) y k 2) （7）其中，L 为输入数据个数， ky 为实际输出数据， ky) 为模型输出。 1.4 T-S 模糊模型参数 ( k yX , k ) ，式（2）可以用矩阵形式表示：对 L 个输入输出对 AP = Y （8） P = Y ,..., ,... ； p [ m p 1 0 p 1 式中， m N p x 11 ] ,..., [ 1= x 11 yy , 2 ,1,..., λ 11 ,..., x Ly m 1 λ N 1 ； T ] ,..., λ N 1 x m 1 x 1 L ,..., λ NL x 1 L ,1,..., λ L 1 x mL ,..., λ NL x mL ⎤ ⎥ ⎥ ⎥ ⎦ （9） 0 ,..., N ,1 λ ⎡ 11 ⎢ ..... ⎢ ⎢ ,1 λ ⎣ L 1 w i N ∑ i 1 = w i A = λ ik = 式中， jkx 表示第 k 个输入数据的第 j 维。由上述可知，式（8）是一个线性规划问题，本文用最小二乘法求解参数矢量 P 。 1.5 模型结构和参数的一体化辨识 T-S 模糊模型的辨识分为结构辨识和参数辨识，许多学者将两部分分开辨识，也取得了不错的效果，但考虑到模型的参数是和模型的结构是密切相关的，当结构变化后，参数需要重新辨识。单独辨识结构的缺点是无法自适应优化模型结构，而获取使模型精度更高、性能更好的结构参数。本文提出模型结构和模型参数一体辨识的方法。该方法的具体步骤如下： m } 1）给定模糊输入划分等级数 N，初始化隶属度函数中心 ,..,2,1 ,..,2,1 jN , c { C = = = i | j i 和宽度 R = j r { i | i = ,..,2,1 jN , = ,..,2,1 m } 。 2）以 C，R 为优化变量，式（7）为目标函数，按照 1.2 所述变尺度优化方法搜索最优结构参数和模型参数。计算目标函数按如下步骤进行： a）以当前的 C，R 建立模糊模型的模糊规则库，并依式（3）把输入数据转换成论域上的基于参考模糊子集的一组模糊集合的可能分布，然后由式(9)计算系数矩阵。 - 3 -

http://www.paper.edu.cn b）由式（8）求解模型参数矢量 P，然后依式（7）计算目标函数值 3）当变尺度混沌优化搜索满足停止条件时，退出循环，得到最优的 C，R 和 P。 2. 水轮机调节系统数学模型描述水轮机调节系统是复杂的非线性系统，由压力引水管道、水轮机、发电机及电网和调速器构成[18]。结构如下图：图 1 水轮机调节系统结构图 2.1 水轮机模型水轮机模型包括基于全特性的非线性模型，基于内特性的非线性模型和基于线性化处理的线性模型。水轮机部分是整个系统中最复杂的环节，非线性强，因为难以用明确数学模型表达，所以在对水轮机调节系统建模仿真、系统辨识等研究时，一般采用线性化水轮机模型，但这样做无疑不能保证模型的精度。本文采用全特性水轮机非线性模型，用下式表达： mt f ( = mt af q ( = q a , M ' n , 1 M ) ' n 1 ) （10）其中，mt 为水轮机力矩，q 为水轮机流量， Ma 为导叶开度， ' 1n 为比转速。式（10）中的非线性函数表征水轮机的全特性曲线，分别与水轮机的流量与力矩特性曲线对应。式（10）中变量均为偏差相对量。 2.2 压力引水管道压力引水管道部分模型可分为刚性水击模型和弹性水击模型，其中弹性水击模型的传递函数由下式表示： 1 48 h 2 −= h w + 33 sT r 1 8 22 sT r sT r 1 2 1 + q （11）其中，h 为引水管道压力， rT 为水击相长， wh 为水管特征系数。求解该模型有特征线法等方法。式（11）中变量均为偏差相对量。 2.3 发电机及电网用机组转子运动方程来描述该部分模型如下式： x = 1 sT a + e g mt （12）式中， x 为机组转速， aT 为机组惯性时间常数， ge 为负荷自调节系数。 2.4 调速器调速器报告控制部分调节器和功率放大部分接力器。模型用如下传递函数框图表示： - 4 -

− − + + + pk k s d T s + d 1 ik s pb (a) 调节器 1 yT s+ 1 (b) 接力器图 2 调速器传函框图 http://www.paper.edu.cn 图中，xg 为频率给定值，x 为机组频率，u 为调节其输出，y 为接力器输出。可以看出，接力器部分存在死区非线性和限幅非线性。 3. 水轮机调节系统的模糊模型辨识 3.1 辨识模糊模型由于实测数据不易获取，本文对水轮机调节系统进行了仿真，利用 T-S 模糊模型辨识方法对仿真系统进行辨识。这里仿真水轮机调节系统在稳定运行时发生小工况扰动的动态过程，分别对系统施加频率扰动和负荷扰动，机组频率和功率及引水管道压力会动态响应，为了节省篇幅，这里系统输出只取机组频率。此时水轮机调节系统可以看作是一个 MISO 系统，系统输入为频率扰动信号和功率扰动信号，系统输出为机组频率。对仿真系统施加的频率扰动端和负荷扰动端分别施加均匀分布的随机信号，信号为标幺值，范围为[-20% 20%]，持续 100s。采用周期 t=0.1s，对输入信号和系统输出信号进行采样，得到的 1000 组输入输出数据对作为模糊模型辨识的训练样本。仿真系统经过标幺化处理，得到输出数据还原成真实值。对训练样本按照本文提出的辨识方法进行辨识，最后得到模糊模型输出和实际输出的对比图，如图 3。由图 3 可以看出，T-S 模糊模型输出与实际输出基本吻合，辨识的模型能较好地跟踪原系统。模型的输出与实际输出的误差见表 1。表 1 模糊模型辨识与仿真精度训练样本10%频扰扰动-10%频率扰动10%负荷扰动-10%频率扰动 0.66802 0.085045 0.084533 0.11052 0.12201 图 3 随机信号输入时的模糊模型辨识结果 - 5 -

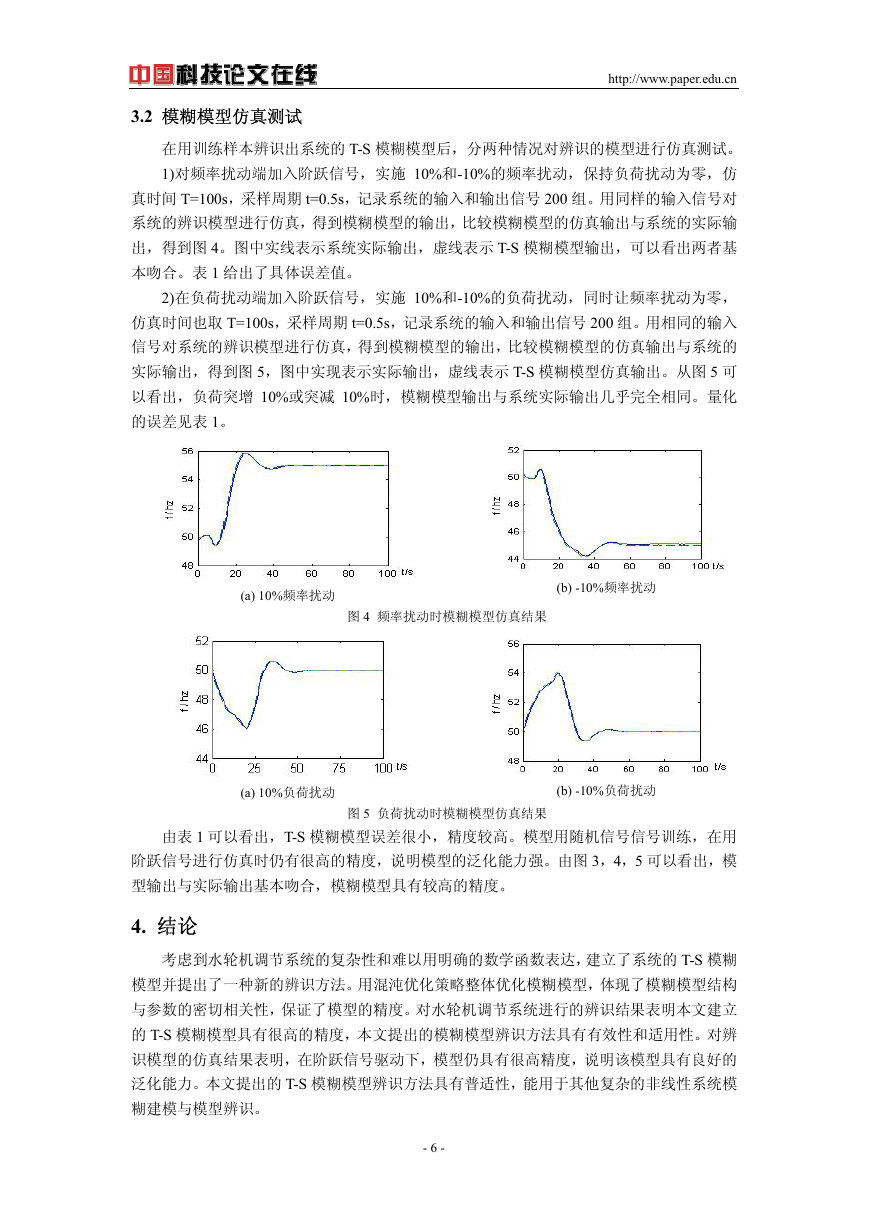
http://www.paper.edu.cn 3.2 模糊模型仿真测试在用训练样本辨识出系统的 T-S 模糊模型后，分两种情况对辨识的模型进行仿真测试。 1)对频率扰动端加入阶跃信号，实施 10%和-10%的频率扰动，保持负荷扰动为零，仿真时间 T=100s，采样周期 t=0.5s，记录系统的输入和输出信号 200 组。用同样的输入信号对系统的辨识模型进行仿真，得到模糊模型的输出，比较模糊模型的仿真输出与系统的实际输出，得到图 4。图中实线表示系统实际输出，虚线表示 T-S 模糊模型输出，可以看出两者基本吻合。表 1 给出了具体误差值。 2)在负荷扰动端加入阶跃信号，实施 10%和-10%的负荷扰动，同时让频率扰动为零，仿真时间也取 T=100s，采样周期 t=0.5s，记录系统的输入和输出信号 200 组。用相同的输入信号对系统的辨识模型进行仿真，得到模糊模型的输出，比较模糊模型的仿真输出与系统的实际输出，得到图 5，图中实现表示实际输出，虚线表示 T-S 模糊模型仿真输出。从图 5 可以看出，负荷突增 10%或突减 10%时，模糊模型输出与系统实际输出几乎完全相同。量化的误差见表 1。 (a) 10%频率扰动 (b) -10%频率扰动图 4 频率扰动时模糊模型仿真结果 (a) 10%负荷扰动 (b) -10%负荷扰动图 5 负荷扰动时模糊模型仿真结果由表 1 可以看出，T-S 模糊模型误差很小，精度较高。模型用随机信号信号训练，在用阶跃信号进行仿真时仍有很高的精度，说明模型的泛化能力强。由图 3，4，5 可以看出，模型输出与实际输出基本吻合，模糊模型具有较高的精度。 4. 结论考虑到水轮机调节系统的复杂性和难以用明确的数学函数表达，建立了系统的 T-S 模糊模型并提出了一种新的辨识方法。用混沌优化策略整体优化模糊模型，体现了模糊模型结构与参数的密切相关性，保证了模型的精度。对水轮机调节系统进行的辨识结果表明本文建立的 T-S 模糊模型具有很高的精度，本文提出的模糊模型辨识方法具有有效性和适用性。对辨识模型的仿真结果表明，在阶跃信号驱动下，模型仍具有很高精度，说明该模型具有良好的泛化能力。本文提出的 T-S 模糊模型辨识方法具有普适性，能用于其他复杂的非线性系统模糊建模与模型辨识。 - 6 -

http://www.paper.edu.cn 参考文献 [1] 张霄元，蒋诚志，洪昕等. 水轮机传递参数在线辨识[J]. 自动化与仪器仪表, 1999, (5):11-13 [2] 杨小东，董宸，卢文华等. 基于遗传算法的水轮发电机组调速系统参数辨识[J]. 继电器, 2006, 34(1): 27-30 [3] 杜庆东，徐凌宇，赵海. 基于神经融合算法的水电厂压力引水系统的辨识[J]. 控制与决策, 2001,16 (增刊): 787-790 [4] 王淑青，李朝晖. 基于自适应模糊神经网络的水轮机特性辨识研究[J]. 武汉大学学报(工学版), 2006, 39 (2): 24-27 [5] Takagi T, Sugeno M Fuzzy identification of systems and its application to modeling and control. IEEE Transactions on Systems, Man and Cybernetics, 1985, 15 (1) : 116～132 [6] Wang Liang, Reza Langari. Complex systems modeling via fuzzy logic. IEEE Transactions on Systems, Man and Cybernetics-A, 1996, 26 (1) : 100～106 [7] Liu Jizhen, Chen Yanqiao. Identification of a boiler-turbine system using T-S fuzzy model[C]. Proceedings of IEEE Tencon, Beijing, 2002: 1278-1281 [8] 朱红霞，沈炯，李益国. 一种新的动态聚类算法及其在热工过程模糊建模中的应用[J]. 中国电机工程学报, 2005, 25(7): 34-40 [9] 李益国，沈炯. 基于 v-支持向量回归的 T-S 模糊模型辨识[J]. 中国电机工程学报, 2006, 26(18):148-153. [10] 王宏伟，顾宏. 基于模糊模型的结构和参数的一体化辨识[J]. 计算机学报, 2006, 29(11):1977-1981. [11] 邓良才, 王广军, 陈红. 锅炉汽温对象的在线模糊辨识[J]. 中国电机工程学报, 2006, 26(18):112-115. [12] 吕剑虹, 陈建勤,刘志远,等．基于模糊规则的热工过程非线性模型的研究[J]．中国电机工程学报,2002,22(11):132－137. [13] 邓良才，王广军，陈红等. 锅炉汽温对象逆动力学过程模糊辨识[J]. 中国电机工程学报, 2007, 27(20):76-80. [14] 于希宁，程锋章，朱丽玲等. 基于改进 T-S 模糊模型辨识算法及其应用[J]. 系统仿真学报, 2007, 19(3): 505-509. [15] 蔡开龙，谢寿生昕，吴勇. 基于 T-S 模糊模型的航空发动机模型辨识[J]. 推进技术, 2007, 28 (2): 194-198 [16] Du Haiping, Zhang Nong. Application of evolving Takagi–Sugeno fuzzy model to nonlinear system identification[J]. Applied Soft Computing, 2008, 8(1):676-686 [17] 张彤，王宏伟，王子才. 变尺度混沌优化方法及其应用[J]. 控制与决策, 1999, 14(3): 285- 287 [18] 沈祖诒. 水轮机调节[M]. 北京: 中国水利水电出版社, 1998 Identification of Hydro-turbine Governing System Based on T-S Fuzzy Model Li Chaoshun, Zhou Jianzhong, An Xueli, Xiang XiuQiao, Li Qingqing, Huang Zhiwei College of Hydroelectric Digitization Engineering, Huazhong University of Science and Technology, Wuhan (430074) Abstract In this paper, Takagi-Sugeno (T-S) fuzzy model of hydro-turbine governing system and a new identification method based on chaos optimization strategy are proposed. Considering the close connection of premise parameters and consequent parameters of T-S fuzzy model, the presented identification method identify them simultaneously, identifying the consequent parameters with least square method and identifying the premise parameters with chaos optimization strategy, which realize the adaptive optimization of T-S fuzzy model. T-S fuzzy model of hydro-turbine governing system is obtained based on the new identification method, with experimental data set of the system when applied frequency disturbance and load disturbance. Then, simulation of the identified fuzzy model of the system is carried out. The results of identification and simulation of T-S fuzzy model of the hydro-turbine system show the identified fuzzy model has relatively high precision and good generalization ability, the identification method is valid. Keywords: hydro-turbine; governor; T-S fuzzy model; system identification; chaos optimization; least square method 作者简介：李超顺（1983-），男，博士研究生，主要从事发电机组故障诊断；周建中(1959－)，通讯作者，男，教授，博士生导师，主要从事人工智能、电力系统自动化相关理论及其应用的研究；安学利（1980-），男，博士研究生，主要从事水轮发电机组故障诊断。 - 7 -

分享到：

赞收藏

资料库

基于T-S模糊模型的水轮机调节系统辨识.pdf

相关推荐

开发技术

热门标签

最新资料