一种基于EKF和和ANN的车载组合导航方法 一种基于 的车载组合导航方法 车载组合导航通常选用GPS和INS作为子系统，由于车载导航中实时性的要求，选用复杂度较低的扩展卡尔曼 （EKF）作为组合导航滤波方法。提出了一种基于神经网络（ANN）和EKF相结合的方法进行组合导航。当 GPS信号有效时，对ANN进行训练；当GPS发生间隔时，ANN的输出分量去修正INS输出偏差。同时考虑到 GPS和INS信号中高频噪声的存在，采用小波变换方法进行预处理去噪，从而提高ANN训练样本的精度。跑车试 验证明，所提出的车载组合导航方法，位置定位平均误差小于3.5 m，可满足车载导航的实际需求。 0 引言引言 全球定位系统（GPS）被广泛应用于 为了克服各自系统的不足，现代车载导航系统通常将两种方法相结合。GPS具有长时精度，因此被用来更新INS位置和速度 分量，并抑制INS误差累计。INS提供精确的短期信息，可以弥补GPS信号遮挡造成的短时间隔。卡尔曼滤波器(KF)是用于随 机模型和先验知识已知情况下的信息融合算法[1]，其缺点如下：(1)在低质量传感器条件下，精确的数学模型难以获得；(2)车 载导航系统和测量设备的先验信息难以精确确定。 针对KF的不足，采用基于人工[2]。文献[2]的研究表明,使用两个MLP的位置、速度更新架构(PVUA)可以在水平方向上提供 准确的位置信息。然而，基于MLP的PVUA系统直接处理INS信息，而不是误差信息，因此其精度难以被准确评估。此 外，MLP算法不能在实时处理中应用。EI-Sheimy提出了基于神经网络的PVUA算法[3]，它可以有效拟合非线性系统，相比KF 算法该算法具有更优异的性能。Sharaf用径向基函数(RBF)神经网络代替MLP[4]。文献[3]、文献[4]中所提两种方法主要受运算 量限制，需要在GPS信号间隔前的所有INS和GPS数据训练ANN系统。因此，Sharaf和Hiliuta提出了自适应神经模糊推理系统 (ANFIS)来实时融合INS和GPS数据[5，6]。ANFIS算法的不足可能导致巨大的计算负担。 此外，低质量的INS受测量噪声影响，信号主要包括高频高斯白噪声分量和低频INS有用信息。因此，为了减弱INS传感器 噪声的不良影响，可以应用小波技术去除高频噪声[7]。A.m.hasn提出一种小波算法来分析比较在不同分辨率水平下INS和GPS 的输出[8]。Tao Zhang提出了一种小波算法来辅助INS、GPS和磁力计组合导航系统中的BP神经网络[9]。Sameh给出了依靠小 波技术提高INS和GPS导航精度的全面分析[10]。 为了优化上述基于ANN算法的性能，本文提出一种基于ANN和 1 基于基于EKF和和ANN的组合导航方法 的组合导航方法 1.1 组合导航方法 组合导航方法 基于EKF和ANN的组合导航系统模型如图1所示。当GPS信号有效时，开关1闭合，开关2断开，EKF融合INS与GPS的输出 结果进行估计，并给出INS的导航参数误差。此时ANN把陀螺仪与加速度计的输出作为其输入，把EKF的输出作为其理想输出 进行在线训练。当GPS信号无效时，开关1断开，开关2闭合，即EKF不工作，陀螺仪与加速度计的输出作为已训练好的神经 网络的输入来预测INS的导航参数误差，并对INS输出的导航信息加以修正。 用EKF估计系统状态时存在误差，因此训练后的ANN不可能严格模拟出系统在各种环境条件下的输出状态。为了提高ANN 的训练样本精度，本文采用小波变换方法对导航子系统数据进行预处理。 1.2 基于小波变换的预处理方法 基于小波变换的预处理方法 该方法首先采用小波变换对GPS和INS子系统输出的导航数据进行高频去噪，然后进行多尺度分析，获取相同分辨率下两者 之间的差别，将其作为样本数据训练ANN。系统的结构框图见图2、图3。 

如图2所示，对GPS和INS三个方向上的位置和速度信息进行小波变换去噪，通过比较在相同分辨率下的GPS和INS位置和 速度分量，确定精确的位置和速度误差，并作为样本数据训练ANN。如图3所示，在GPS信号失效时ANN的输出作为EKF的输 入分量，用来修正INS的导航信息，获得系统状态的最优估计。 2 实验结果性能分析 实验结果性能分析 2.1 实验设备 实验设备 为验证所提出的车载导航滤波方法有效性，进行了车载实验。车载实验使用汽车上装载的不同性能的GPS和INS设备，包括 GPS RTK接收仪器Leica GS10和战术精度的INS Crossbow的 AHR400CA设备，以及导航精度的INS Honywell的IMU1700设 备。 在车载实验中，IMU1700和Leica GS10设备构成的组合导航系统，定位精度可在分米级别，用作参考路径；GPS数据仅使 用Leica GS10的伪距定位，与Crossbow低精度设备一起用来测试验证本算法的有效性。 2.2 车载路线 车载路线 车载路线如图4所示，逆时针方向绕行2圈，每圈约25 min。车载路线被设计为包含GPS无遮挡环境、半遮挡环境和全遮挡 环境。其中全遮挡环境下GPS卫星接收数目小于4个。 在车载实验的初始阶段，汽车来回绕8字形圈进行INS初始化，如图4箭头所示，持续大概6 min。其中前3 min的观测值，用 来作为陀螺和加速度计偏差的预测，而初始方向从车载的运行轨迹可粗略推算出。 2.3 车载实验卫星可见性 车载实验卫星可见性 表1为车载实验过程对GPS间隔进行的统计数据，从表中可以看出实验过程中会出现GPS间隔（GPS可见卫星数目小于 

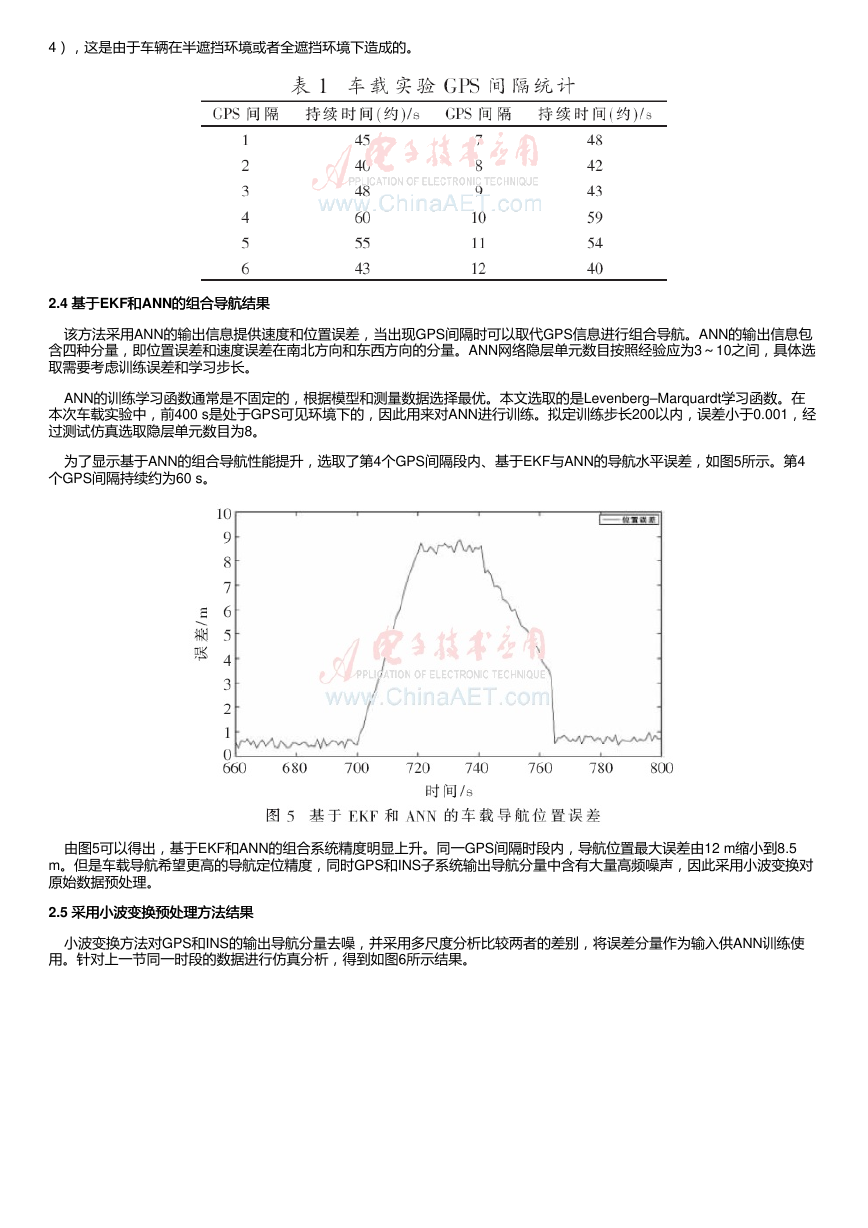
4），这是由于车辆在半遮挡环境或者全遮挡环境下造成的。 2.4 基于基于EKF和和ANN的组合导航结果 的组合导航结果 该方法采用ANN的输出信息提供速度和位置误差，当出现GPS间隔时可以取代GPS信息进行组合导航。ANN的输出信息包 含四种分量，即位置误差和速度误差在南北方向和东西方向的分量。ANN网络隐层单元数目按照经验应为3～10之间，具体选 取需要考虑训练误差和学习步长。 ANN的训练学习函数通常是不固定的，根据模型和测量数据选择最优。本文选取的是Levenberg–Marquardt学习函数。在 本次车载实验中，前400 s是处于GPS可见环境下的，因此用来对ANN进行训练。拟定训练步长200以内，误差小于0.001，经 过测试仿真选取隐层单元数目为8。 为了显示基于ANN的组合导航性能提升，选取了第4个GPS间隔段内、基于EKF与ANN的导航水平误差，如图5所示。第4 个GPS间隔持续约为60 s。 由图5可以得出，基于EKF和ANN的组合系统精度明显上升。同一GPS间隔时段内，导航位置最大误差由12 m缩小到8.5 m。但是车载导航希望更高的导航定位精度，同时GPS和INS子系统输出导航分量中含有大量高频噪声，因此采用小波变换对 原始数据预处理。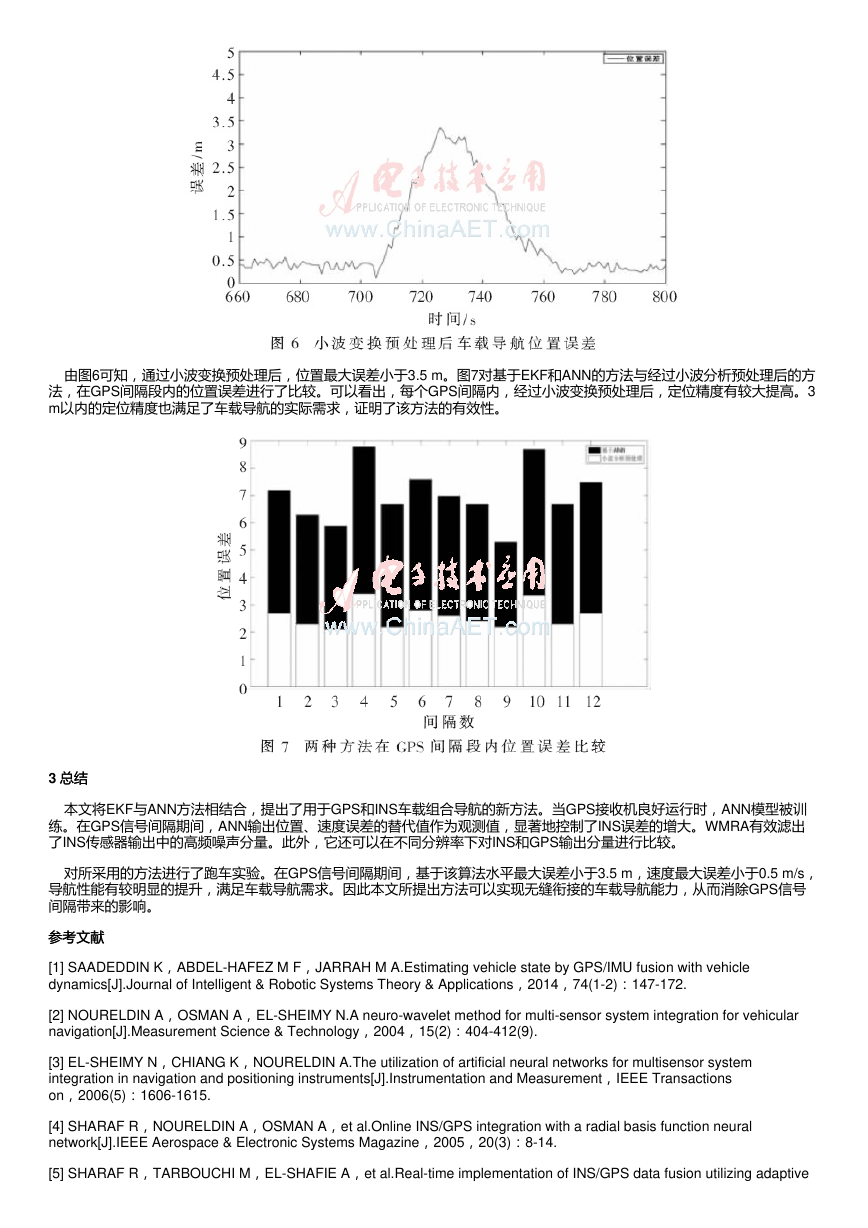 2.5 采用小波变换预处理方法结果 采用小波变换预处理方法结果 小波变换方法对GPS和INS的输出导航分量去噪，并采用多尺度分析比较两者的差别，将误差分量作为输入供ANN训练使 用。针对上一节同一时段的数据进行仿真分析，得到如图6所示结果。 

由图6可知，通过小波变换预处理后，位置最大误差小于3.5 m。图7对基于EKF和ANN的方法与经过小波分析预处理后的方 法，在GPS间隔段内的位置误差进行了比较。可以看出，每个GPS间隔内，经过小波变换预处理后，定位精度有较大提高。3 m以内的定位精度也满足了车载导航的实际需求，证明了该方法的有效性。 3 总结总结 本文将EKF与ANN方法相结合，提出了用于GPS和INS车载组合导航的新方法。当GPS接收机良好运行时，ANN模型被训 练。在GPS信号间隔期间，ANN输出位置、速度误差的替代值作为观测值，显著地控制了INS误差的增大。WMRA有效滤出 了INS传感器输出中的高频噪声分量。此外，它还可以在不同分辨率下对INS和GPS输出分量进行比较。 对所采用的方法进行了跑车实验。在GPS信号间隔期间，基于该算法水平最大误差小于3.5 m，速度最大误差小于0.5 m/s， 导航性能有较明显的提升，满足车载导航需求。因此本文所提出方法可以实现无缝衔接的车载导航能力，从而消除GPS信号 间隔带来的影响。 参考文献 参考文献 [1] SAADEDDIN K，ABDEL-HAFEZ M F，JARRAH M A.Estimating vehicle state by GPS/IMU fusion with vehicle dynamics[J].Journal of Intelligent & Robotic Systems Theory & Applications，2014，74(1-2)：147-172. [2] NOURELDIN A，OSMAN A，EL-SHEIMY N.A neuro-wavelet method for multi-sensor system integration for vehicular navigation[J].Measurement Science & Technology，2004，15(2)：404-412(9). [3] EL-SHEIMY N，CHIANG K，NOURELDIN A.The utilization of artificial neural networks for multisensor system integration in navigation and positioning instruments[J].Instrumentation and Measurement，IEEE Transactions on，2006(5)：1606-1615. [4] SHARAF R，NOURELDIN A，OSMAN A，et al.Online INS/GPS integration with a radial basis function neural network[J].IEEE Aerospace & Electronic Systems Magazine，2005，20(3)：8-14. [5] SHARAF R，TARBOUCHI M，EL-SHAFIE A，et al.Real-time implementation of INS/GPS data fusion utilizing adaptive 

neuro-fuzzy inference system[C].Proceedings of the 2005 National Technical Meeting of The Institute of Navigation，San Diego，CA，2005. [6] HILIUTA A，LANDRY R，GAGNON F.Fuzzy corrections in a GPS/INS hybrid navigation system[J].Aerospace & Electronic Systems IEEE Transactions on，2004，40(2)：591-600. [7] 杨丽.遗传优化小波神经网络在组合导航中的应用研究[D].南京：南京航空航天大学，2010. [8] HASAN A M，SAMSUDIN K，RAMLI A R，et al.Comparative study on wavelet filter and thresholding selection for GPS/INS data fusion[J].International Journal of Wavelets Multiresolution & Information Processing，2011，8(3)：457-473. [9] ZHANG T，XU X.A new method of seamless land navigation for GPS/INS integrated system[J].Measurement，2012，45(4)：691-701. [10] NASSAR S，ELSHEIMY N.Wavelet analysis for improving INS and INS/DGPS navigation accuracy[J].Journal of Navigation，2005，58(1)：119-134.