连玉君-Logit模型STATA.pdf-资料库

weixin_46178806-12097885-4744300845374565939.pdf-第1页.png

第1页 / 共38页

weixin_46178806-12097885-4744300845374565939.pdf-第2页.png

第2页 / 共38页

weixin_46178806-12097885-4744300845374565939.pdf-第3页.png

第3页 / 共38页

weixin_46178806-12097885-4744300845374565939.pdf-第4页.png

第4页 / 共38页

weixin_46178806-12097885-4744300845374565939.pdf-第5页.png

第5页 / 共38页

weixin_46178806-12097885-4744300845374565939.pdf-第6页.png

第6页 / 共38页

weixin_46178806-12097885-4744300845374565939.pdf-第7页.png

第7页 / 共38页

weixin_46178806-12097885-4744300845374565939.pdf-第8页.png

第8页 / 共38页

计量分析与 STATA 应用钟经樊连玉君关于作者：钟经樊台湾中央研究院经济研究所　　　　　连玉君中山大学岭南学院金融系中文版本：版本 2.0，二○一○年六月

目录第十五章 Logistic 模型 . 15.1 简介 . . . 15.2 二元 Logit 模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15.2.1 二项分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15.2.2 Logit 变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15.2.3 Logistic 模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15.2.4 估计 . . . 15.2.5 假设检验 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15.2.6 模型的解释和拟合优度 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15.4 STATA 中有关 Logitech 模型的命令概览 . . . . . . . . . . . . . . . . . . . . . . . . . 15.3 多元 Logit 模型 . . . 15.3.1 估计 . . . 15.3.2 假设检验 . . 15.3.3 拟合优度 . . . 15.3.4 模型的解释 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 1 2 2 3 6 7 12 12 18 27 28 33 III

第十五章 Logistic 模型 15.1 简介在过去的二十年中，logistic 模型在众多领域得到了广泛的应用，甚至成为部分领域的标准分析方法。 logistic 模型与线性模型的最大区别就在于前者的被解释变量是二元变量 (binary) 或取值有限的离散变量 (dichotomous)。这种区别使得两种模型的参数设定和假设条件都存在差异。在充分考虑这些差异的前提下，前面介绍的用于分析线性模型的基本规则同样适用于分析 logistic 模型。当然，由于 logistic 模型的非线性特征，在分析过程中还需要引入一些新的统计和评估方法。 15.2 二元 Logit 模型 15.2.1 二项分布假设我们想要研究上市公司债务融资行为的决定因素，被解释变量 yi 为上市公司是否发行债务。显然，yi 是一个二元变量，只有 0 和 1 两个取值，定义如下： yi = 1 若第 i 家公司发行债务 0 其它 (15-1) 我们可以将 yi 视为随机变量 Yi 的实现值，Yi 有 1 和 0 两个取值，相应的概率分别为 πi 和 1 − πi 。 Yi 服从贝努力 (Bernoulli) 分布，参数为 πi ，可表示为 Pr Yi = yi yi i (1 − πi )1−yi , 其中， yi = 0, 1. (15-2) = π 显然，若 yi = 1，则上式为 πi ；若 yi = 0，则上式为 1 − πi 。易于证明，Yi 的期望和方差分别为： E(Yi ) = µi = πi Var(Yi ) = σi = πi (1 − πi ) 1

15.2二元LOGIT模型 2 可见，期望和方差都决定于 πi 。任何影响概率的因素不但会影响观察值的的均值，也会影响其方差。这表明前面介绍的线性模型无法用于分析二元变量，因为线性模型假设方差是固定不变的。 15.2.2 Logit 变换线性变换为了使上述模型更富有弹性，我们假设概率 πi 受一系列变量的影响，设定为 xi 。一个非 i βββ, 其中，βββ 为系数向量。该模型通常直觉的想法是把二者之间的关系设定为线性函数： πi = x 常称为线性概率模型，采用普通最小二乘法估计即可。其主要缺陷在于：由于等式左边的 πi 表示概率，所以必须介于 0 和 1 之间，而右边的线性组合项则可能取任何值，所以在不对模型做严格约束的情况下，我们很难保证模型的预测值介于合理的范围内。 logit 变换因此，我们必须对概率 πi 进行变换以消除对其取值范围的约束，继而把变换后的数值设定为解释变量 xi 的线性函数。处理过程包括两个步骤。第一步，我们依据概率 πi 来定义胜算比(odds) ： i = πi 1 − πi , (15-4) 即 yi = 1 的概率 πi 与 yi = 0 的概率 (1 − πi) 的比值。显然，胜算比可以取任意非负值，如此便可消除上限约束。第二步，取对数以计算 logit 或 log-odds logit(πi ) = ln(i ) = ln πi 1 − πi (15-5) 这样我们就可以去除下限约束。因为，随着概率 πi 趋近于 0 ，logit 将趋近于 −∞ ；而当概率 πi 趋近于 1 ，logit 将趋近于 +∞ 。因此，通过以上变换，logit 将概率 πi 的取值范围从 (0, 1) 映射至整个实数轴。显然，如果概率为 0.5，胜算比为 1，相应的 logit 为 0。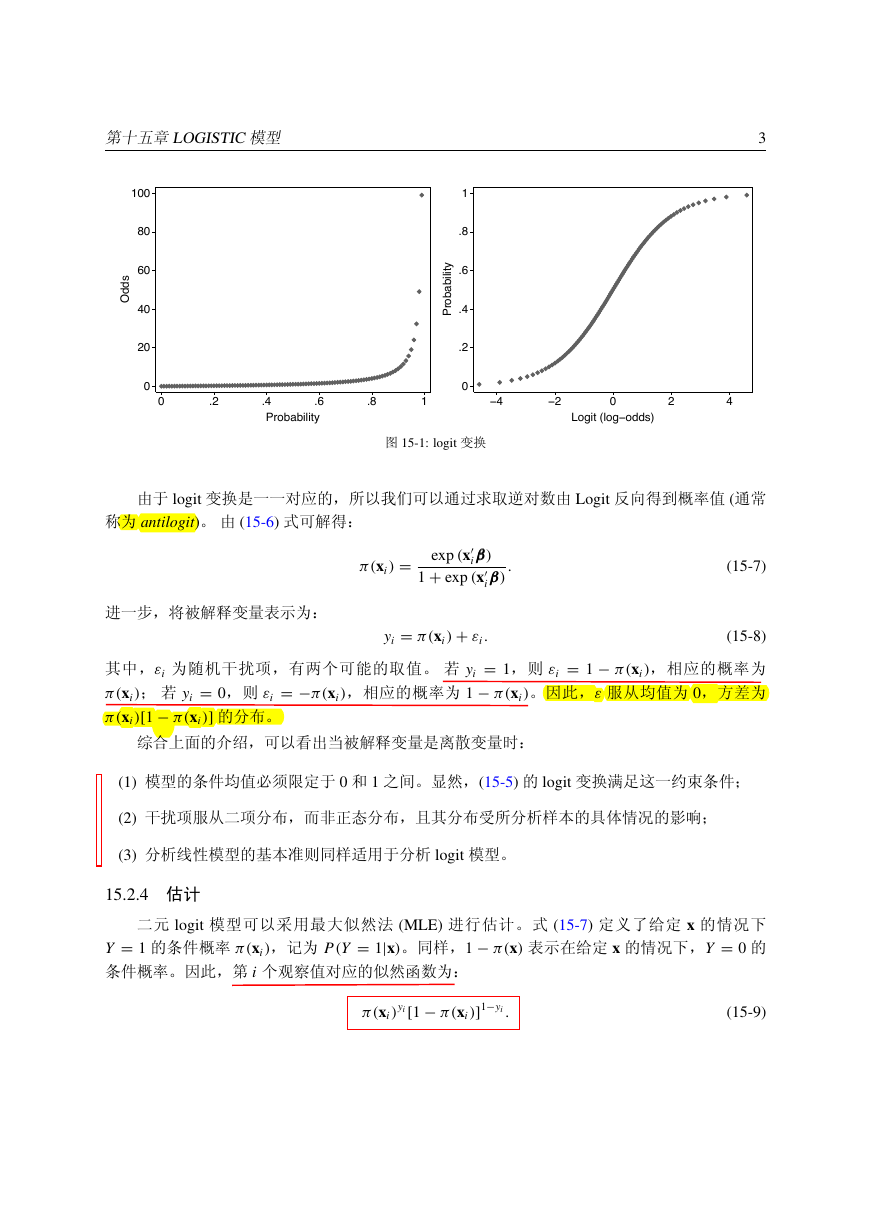logit 为负表示概率小于 0.5，反之则表示概率大于 0.5。图 15-1 说明了上述变换的对应关系。 15.2.3 Logistic 模型在完成了上述变换后，我们就可以定义 Logistic 回归模型了，此时我们假设概率 πi 的 Logit 变换 (而非概率 πi 本身) 服从线性模型，即 logit(πi ) = ln 其中，xi 为解释变量构成向量，βββ 为系数向量。 πi 1 − πi = x i βββ, (15-6)

第十五章LOGISTIC模型 3 图 15-1: logit 变换由于 logit 变换是一一对应的，所以我们可以通过求取逆对数由 Logit 反向得到概率值 (通常称为 antilogit)。由 (15-6) 式可解得： π(xi ) = exp (x i βββ) 1 + exp (x i βββ) . (15-7) 进一步，将被解释变量表示为： (15-8) 其中，εi 为随机干扰项，有两个可能的取值。若 yi = 1，则 εi = 1 − π(xi )，相应的概率为 π(xi )；若 yi = 0，则 εi = −π(xi )，相应的概率为 1 − π(xi )。因此，ε 服从均值为 0，方差为 π(xi )[1 − π(xi )] 的分布。 yi = π(xi ) + εi . 综合上面的介绍，可以看出当被解释变量是离散变量时： (1) 模型的条件均值必须限定于 0 和 1 之间。显然，(15-5) 的 logit 变换满足这一约束条件； (2) 干扰项服从二项分布，而非正态分布，且其分布受所分析样本的具体情况的影响； (3) 分析线性模型的基本准则同样适用于分析 logit 模型。 15.2.4 估计二元 logit 模型可以采用最大似然法 (MLE) 进行估计。式 (15-7) 定义了给定 x 的情况下 Y = 1 的条件概率 π(xi )，记为 P(Y = 1|x)。同样，1 − π(x) 表示在给定 x 的情况下，Y = 0 的条件概率。因此，第 i 个观察值对应的似然函数为： π(xi )yi [1 − π(xi )]1−yi . (15-9) 020406080100Odds0.2.4.6.81Probability0.2.4.6.81Probability−4−2024Logit (log−odds)

15.2二元LOGIT模型 4 假设所有观察值都是彼此独立的，则样本似然函数为所有观察值对应的似然函数之积： π(xi )yi [1 − π(xi )]1−yi . (15-10) 我们的目的在于求得使 (15-10) 式最大时对应参数估计值 ˆβββ。为了方便求解，定义对数似 yi ln [π(xi )] + (1 − yi ) ln [1 − π(xi )] (15-11) L(βββ) = n i=1 ln L(βββ) = n i=1 = n 然函数：一阶条件为： ∂ ln L(βββ) (yi − πi )xi = 0. (15-12) 由 (15-12) 式可知：(1) 若 xi 中包含常数项，则 ¯ˆπi = ¯yi ，即预测概率的平均值等于样本中 yi = 1 的比例。 (2) 如果我们将 yi − πi 看作一般化残差 (generalized residual)，则 (15-12) 式与线性回归模型中的正交条件具有相似的含义。 i=1 ∂βββ 采用牛顿迭代法可以很方便地得到参数的估计值。我们可以进一步求取二阶偏导如下： H(βββ) = − ∂2 ln L ∂βββ∂βββ = − n i=1 πi (1 − πi )xix i . (15-13) 通常把 H 称为海赛矩阵 (Hessian)。由于 Hessian 始终为负定矩阵，所以对数似然函数可以在几次迭代后便达到全局收敛。参数的方差-协方差矩阵可以利用 Hessian 的逆矩阵求得，即 Var (βββ) = −H−1(βββ). (15-14) 在多数情况下，我们都很难写出该矩阵的具体形式。因此，我们将该矩阵的第 j 个对角元素记为 Var(β j )，它是 ˆβ j 的方差；用 Cov(β j , βl ) 表示任意非对角元素，它是 ˆβ j 和 ˆβl 的协方差。因此，方差-协方差矩阵的估计值可表示为 Var(ˆβββ)。我们采用 Var( ˆβ j ) 和 Cov( ˆβ j , ˆβl )， j, l = 0, 1, 2,··· , k 表示该矩阵中的元素。至此，系数的标准误可求取如下： se( ˆβ j ) = Var( ˆβ j ), for j = 0, 1, 2,··· , k. (15-15) 在 Stata 中，Logit 模型均采用最大似然法 (MLE) 进行估计。虽然在大样本下，ML 估计量是一致、有效，并渐进地服从正态分布的，但其小样本性质在多数情况下都不得而知。因此，在实证分析过程中，样本容量的大小对估计结果有很大的影响。在针对小样本使用 ML 时，Long (1997, p.54) 给出了如下建议： 1. 当样本数小于 100 时，使用 ML 是比较危险的，样本数大于 500 效果较佳，当然，这些取值还决定于模型和数据的具体特征；

资料库

连玉君-Logit模型STATA.pdf

相关推荐

开发技术

热门标签

最新资料