基于谱元法和波传播的裂纹梁损伤检测.pdf-资料库

中国科技论文在线 http://www.paper.edu.cn 基于谱元法和波传播的裂纹梁损伤检测# 王丹生，金涛，张猛，朱宏平* （华中科技大学土木工程与力学学院，武汉 430074）摘要：基于波动理论和弯曲弹簧模型推导了裂纹梁谱单元刚度矩阵。阐述了基于谱元法（Spectral Element Method, SEM）和波传播的结构损伤检测方法的基本原理，并利用该检测方法对悬臂梁结构进行了裂纹识别数值研究。研究结果发现：利用谱元法计算得到的梁端部位移曲线在裂纹位置有明显的反射波；而且，随着裂纹尺寸的增大，反射波更加明显。由此可知，基于谱元法和波传播的结构损伤识别方法不仅能准确地识别出悬臂梁的损伤位置，还能定性地识别裂纹损伤的程度。关键词：损伤检测；谱元法；波传播；悬臂梁；裂纹梁中图分类号：O326 DAMAGE DETECTION IN A CRACKED BEAM BASED ON SPECTRAL ELEMENT METHOD AND WAVE PROPAGATION WANG Dansheng, JIN Tao, ZHANG Meng, ZHU Hongping (School of Civil Engineering and Mechanics, Huazhong University of Science and Technology, Wuhan 430074) Abstract: The spectral stiffness matrix of cracked beam element is deduced based on wave motion theory and a rotational spring model. The basic principle of a structural damage detection method based on Spectral Element Method (SEM) and wave propagation is also introduced in this paper. Numerical study on a cantilever beam for crack detection based on the proposed method is conducted. From the study results one can find that the displacement response curve at the free end of the beam is calculated using the SEM and there is a visible reverberation at the crack location of the beam; and the reverberation becomes more remarkable with the increase of crack size. So the detection method based on SEM and wave propagation has not only the ability to identify the location of damage of beam structures, but also the ability to predict the extent of crack damage. Key words: Damage detection; Spectral element method; wave propagation; cantilever beam；cracked beam 0 引言近十几年来，基于结构动态响应的损伤检测已成为国内外研究的热点。由于结构振动特性是结构物理参数的函数，结构损伤即意味着结构物理参数的改变，而物理参数的改变必然引起结构振动特性的改变。通过获取结构在不同阶段的振动特性，并对结构振动特性的变化进行分析及处理，有可能获得结构物理参数的变化情况，从而实现对结构进行损伤检测的目的。在基于结构动态响应对结构进行损伤检测数值研究时，我们往往使用有限元法来对结构进行建模和计算。为了满足工程计算精度，采用有限元法对结构进行动力分析时需要大量划分单元，从而导致计算量大大增加。特别是在结构动力分析的高频部分，要想得到精确的分析结果，单元数目要求更多。为了克服有限元的局限性，文献[1-5]提出了一种基于连续质量基金项目：国家自然科学基金（50925828,50778077）；高等学校博士学科点专项科研基金（20070487099）作者简介：王丹生（1973-），男，副教授，主要研究方向：结构健康监测. E-mail: danshw@163.com - 1 -

中国科技论文在线 http://www.paper.edu.cn 体系动力响应分析和快速傅里叶变换（FFT）的谱元法。该方法对于连续均匀的梁、杆构件，不论其长度有多大，只需划分一个单元即可得到精确的解答[1]。本文利用谱元法和波动理论对裂纹梁进行建模，并将裂纹模拟为弯曲弹簧，推导了裂纹梁谱单元刚度矩阵；在此基础上计算得到外荷载作用下梁结构的位移波动曲线，通过该位移波曲线即可识别裂纹损伤的位置。 1 裂纹梁谱单元刚度矩阵一个具有一条横向开放、不扩展裂纹的裂纹梁谱单元如图 1 所示。该单元有左右两个节点，每个节点有两个自由度—横向位移和转角。单元的长度为 L，横截面积为 A。裂纹用一个无量纲的弯曲弹簧来模拟。弹簧的无因次刚度为。 1L θ 图 1 裂纹梁谱单元模型 Fig. 1 Spectral cracked beam element model 裂纹梁左、右两端的节点谱位移分别具有下列形式[6]： k L x ) − n ik L x − ik x n k x n − − − ( ) ( n 1 1 ˆ ( ) u x 1 A e = 5 = Ae 1 ik L x ( + n 1 − ) + A e 2 + A e 6 ˆ ( ) u x 2 + − A e 3 A e 7 + − k L x + n ( 1 ) − ik L L x + − ( ( n 1 + A e 4 )) ∈ , ( x ( k L L x + n − 1 L 0, 1 x )) , （1） ∈ L L 1 , （2） + − A e 8 式中代表裂纹位置，L 是梁的总长，是波数，由下式计算可得： k n = ω ⎛ ⎜ ⎝ n A ρ EJ 1/4 ⎞ ⎟ ⎠ （3）式中梁的材料密度，A 是单元横截面积，E 是杨氏模量，J 是单元截面的惯性矩，是频率。梁单元的左端（x=0）边界条件： ˆ u x ( ) 1 = ˆ q 1 , ˆ ( ) u x ∂ 1 x ∂ = ˆ q 2 （4） − 梁中裂纹处的相容条件： ˆ u x ( ) = 1 ˆ u x ( ) ∂ 2 x ∂ ˆ u x ( ) 2 1 x 2 ∂ ˆ u x ( ) 3 1 x 3 ∂ ˆ u x ( ) 2 ˆ u x ( ) ∂ 1 x ∂ ˆ u x ( ) 2 ∂ 2 x 2 ∂ ˆ u x ( ) 2 x 3 ∂ 梁单元的右端（x=L）边界条件： = = = ∂ ∂ ∂ 3 ∂ θ 2 ˆ u x ( ) 1 x 2 ∂ （5） ˆ u x ( ) 2 = ˆ q 3 , = ˆ q 4 （6） ˆ ( ) u x ∂ 2 x ∂ - 2 -

中国科技论文在线 http://www.paper.edu.cn 将式（1）和（2）代入到上述边界条件可得如下矩阵方程： 1= −A D q （7）式中： D ⎡ ⎢ ⎢ ⎢ ⎢ ⎢= ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ik ( n 1 ik − a k a ) 2 + θ n n ik a 2 − n ik a 3 n 0 0 ( k n A q k b ) 2 n n 1 k − b − θ k b 2 n k b 3 − n 0 0 =[ =[ 4 4 A A A A A A A A ]T （8） 1 8 2 6 7 ˆ ˆ ˆ ˆ q q q q ]T （9） 3 1 2 a 0 ik a 0 n a 1 − ik a ik 2 − − n n k a k 2 2 − n n ik a ik 3 3 − − n n f 0 ik f 0 − n 3 5 0 0 0 0 b k b n 1 k k − − θ k 2 n k 3 n 0 0 0 0 b − k b − n k b 2 − n k b 3 n g k g n 0 0 d − k d n k d 2 − n k d 3 − n 1 k 0 0 c − ik c n k c 2 n ik c 3 n 1 ik （10） ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦ − 2 n n n n n k θ − e ik L n 1 其中， a = （11）此外，将式（1）和（2）分别对 x 进行二阶和三阶差分可得到谱单元节点力的矩阵方程： =F BA （12） ik L L − 1 k L L − n 1 ik L n k L n 1 k L n = = = = = b d g e c e e e e f , , , , , ( n − − − − ( ) − ) 式中： ˆ 3 ˆ ˆ ˆ F F F F F =[ 1 4 2 k b k a 0 3 3 n n k a k b 0 2 2 n n ik f 0 0 3 − n k f 0 0 2 − n 将式（7）代入到式（12）可得： ik 3 n k 2 − n 0 0 k 3 − n k 2 n 0 0 ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ − − EI B = ]T （13） 0 0 k g 3 n k g 2 n （14） 0 0 ik 3 n k 2 − n 0 0 k 3 − n k 2 n ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ 令 K BD ，则有 = − 1 F BD q （15） = 1 − =F Kq （16）其中K 为与频率相关的裂纹梁谱单元刚度矩阵。 2 裂纹模型为了描述裂纹梁的弯曲振动问题，裂纹可用一个弯曲弹簧来模拟。弹簧刚度可表示为 [7] θ= EI ζ L ， ζ= (5.346 H EI f H H ) ( / c ) (17) 式中ζ为弹簧柔度系数， cH 为裂纹深度，H 为梁的高度，数。 HHf ( c ) 为无因次局部导纳函 f H H ( c 2 ) 1.8624( = 76.81( 66.56( + + H H ) 3.95( − c H H ) 126.9( − H H ) 10 6 c c 3 H H ) c H H c + ) 7 16.37( 172( + c H H H H c 4 ) ) 8 − − 37.226( 43.97( H H ) H H ) 9 c c 5 (18) - 3 -

中国科技论文在线 3 基于谱元法的裂纹梁损伤识别步骤 http://www.paper.edu.cn 本文使用谱元法对梁结构进行建模并且计算动力响应，进而实现结构的损伤识别，具体的步骤如下：（1）利用 FFT 将时域内的荷载变换成频率内的荷载；（2）利用式（15）得到与频率 iω相关的裂纹梁谱单元刚度矩阵；（3）与有限元法类似，如有多个单元，则将谱单元刚度矩阵在频率 iω处组装成整体刚度矩阵；（4）考虑梁结构的边界条件，求出频率 iω处的节点位移向量；（5）对频域内的位移向量进行 FFT 逆变化，求得结构在时域内的动态响应。并从该位移响应曲线上的反射波识别出裂纹的位置。 4 数值算例 4.1 模型参数及动荷载本文用于分析的悬臂梁模型如图 2 所示，其长度 L=3m，弹性模量 E=2.09e11Mpa、密度ρ=7800kg/m3，截面积 A=0.0008m2,泊松比ν=0.3。悬臂梁的材料参数保持不变，假设在梁的中点部位存在裂纹。为了讨论的方便，假定梁截面中的裂纹属于开放型不扩展裂纹，不考虑结构振动时裂纹的闭合效应，并且认为裂纹部分的开裂深度相同。图 2 裂纹悬臂梁 Fig. 2 Cracked cantilever beam 在梁上右端点作用的剪力方向动荷载时间历程曲线及其频谱曲线如图 3 所示，荷载的峰值为 1N，荷载历程为 0.0001s。 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0 0.2 0.4 0.6 0.8 1.2 1.4 1.6 1.8 1 t(s) 2 x 10-3 50 45 40 35 30 25 20 15 10 5 0 0 1 2 3 5 4 6 Frequency (Hz) 7 8 9 图 3 动荷载时程曲线及其频谱曲线 Fig. 3 Dynamic load-time curve and its FFT spectrum curve - 4 - 10 x 105

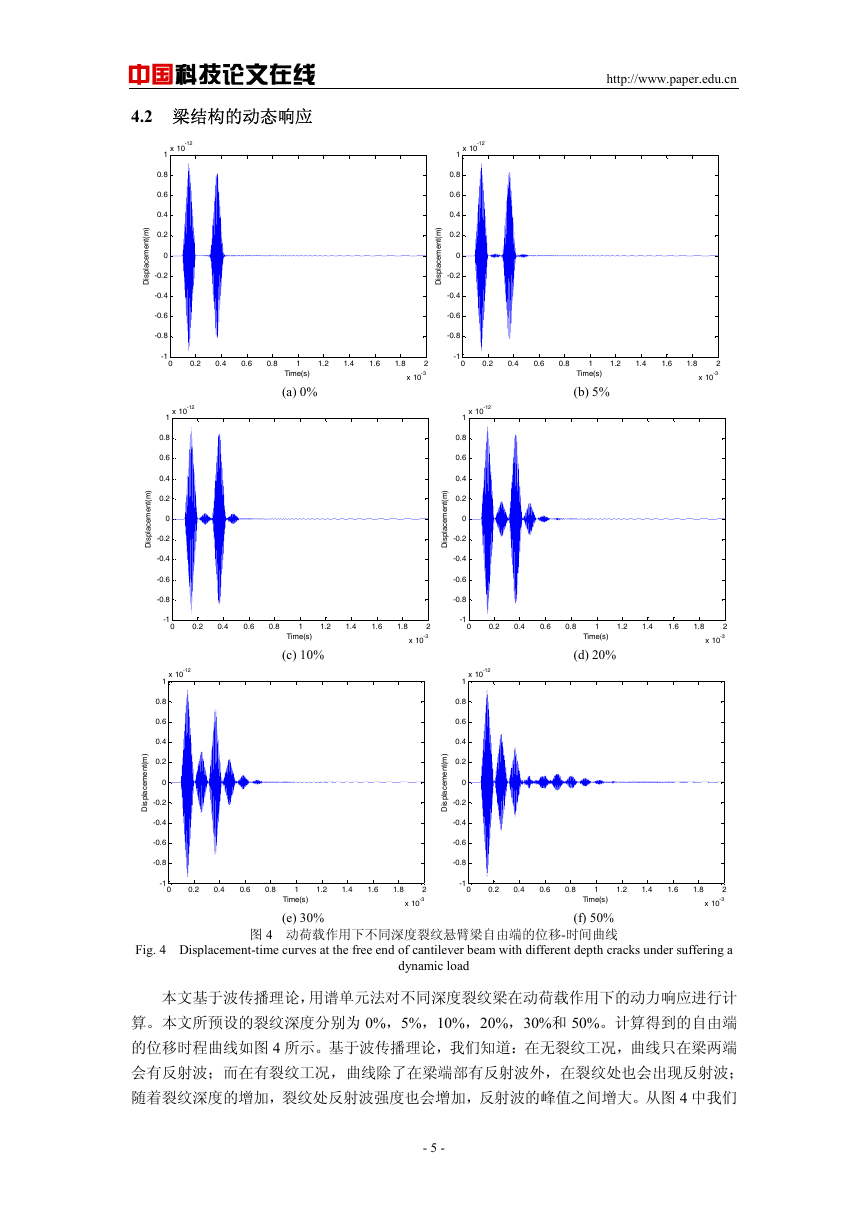
中国科技论文在线 4.2 梁结构的动态响应 http://www.paper.edu.cn x 10-12 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 x 10-12 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 ) m ( t n e m e c a p s D i l Time(s) (a) 0% (b) 5% Time(s) 2 x 10-3 2 x 10-3 Fig. 4 Displacement-time curves at the free end of cantilever beam with different depth cracks under suffering a dynamic load 本文基于波传播理论，用谱单元法对不同深度裂纹梁在动荷载作用下的动力响应进行计算。本文所预设的裂纹深度分别为 0%，5%，10%，20%，30%和 50%。计算得到的自由端的位移时程曲线如图 4 所示。基于波传播理论，我们知道：在无裂纹工况，曲线只在梁两端会有反射波；而在有裂纹工况，曲线除了在梁端部有反射波外，在裂纹处也会出现反射波；随着裂纹深度的增加，裂纹处反射波强度也会增加，反射波的峰值之间增大。从图 4 中我们 - 5 - ) m ( t n e m e c a p s D i l ) m ( t n e m e c a p s D i l ) m ( t n e m e c a p s D i l x 10-12 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 x 10-12 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 ) m ( t n e m e c a p s D i l Time(s) (c) 10% (d) 20% Time(s) 2 x 10-3 x 10-12 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 x 10-12 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 ) m ( t n e m e c a p s D i l Time(s) (e) 30% (f) 50% Time(s) 图 4 动荷载作用下不同深度裂纹悬臂梁自由端的位移-时间曲线 2 x 10-3 2 x 10-3 2 x 10-3

中国科技论文在线 http://www.paper.edu.cn 可明显发现此规律，因此我们通过梁中部的反射波，从而可以准确地判断梁中裂纹就位于梁的中点。此外，我们还可以发现，随着裂纹深度的加大，由于波动能量在裂纹处的耗散导致另一端部反射波的衰减，即导致第一个波峰明显的高于第三个波峰。 5 结论本文利用谱元法和波传播理论对裂纹梁进行建模和分析，并用弯曲弹簧模型来模拟梁中的裂纹。推导了裂纹梁谱单元刚度矩阵，并在此基础上介绍了一种裂纹梁损伤检测方法。利用该方法对裂纹悬臂梁进行了多工况的裂纹损伤检测数值研究，研究结果发现，利用谱元法计算得到的梁端位移波曲线不仅在梁端部有反射波，而且在梁中点也有反射波；并且随着裂纹尺寸的加大，梁中点的反射波幅值增大，而梁另一端部的反射波幅值则逐渐减小。由此，我们可以依据波传播理论确定裂纹就在梁的跨中位置，这和预设的两裂纹位置是一致的，而且从裂纹处反射波幅值的变化还可以定性地确定裂纹损伤的程度。 [参考文献] (References) [1] DOLYLE J F, FARRIS T N. A spectrally formulated finite element for flexural wave propagation in beam [J]. The International Journal of Analytical and Experimental Modal Analysis, 1990, 5(2): 99~107. [2] DOLYLE J F, FARRIS T N. A spectrally formulated finite element for flexural wave propagation in 3-D frame structures [J]. The International Journal of Analytical and Experimental Modal Analysis, 1990, 5(4): 223~237. [3] DOLYLE J F. A spectrally formulated finite element for longitudinal wave propagation [J]. The International Journal of Analytical and Experimental Modal Analysis, 1988, 3(1): 125~134 [4] DOLYLE J F. Wave Propagation in Structures: Spectral Analysis Using Fast Discrete Fourier Transforms, [5] LEE U, KIM J, LEUNG A Y T. The spectral element method in structural dynamics [J]. The Shock and New York: Springer-Verlag, 1997 Vibration Digest, 2000, 32(6): 451~465 [6] KRAWCZUK M. Application of spectral beam finite element with a crack and iterative search technique for damage detection, Finite Element in Analysis and Design, 2002, 38: 537~548 [7] PAIPERIS S. A, DIMAROGONAS A D. Analytical Methods in Rotor Dynamics, London: Elsevier Applied Science. 1986. - 6 -

资料库

基于谱元法和波传播的裂纹梁损伤检测.pdf

相关推荐

开发技术

热门标签

最新资料