2014年山西省中考数学真题.doc-资料库

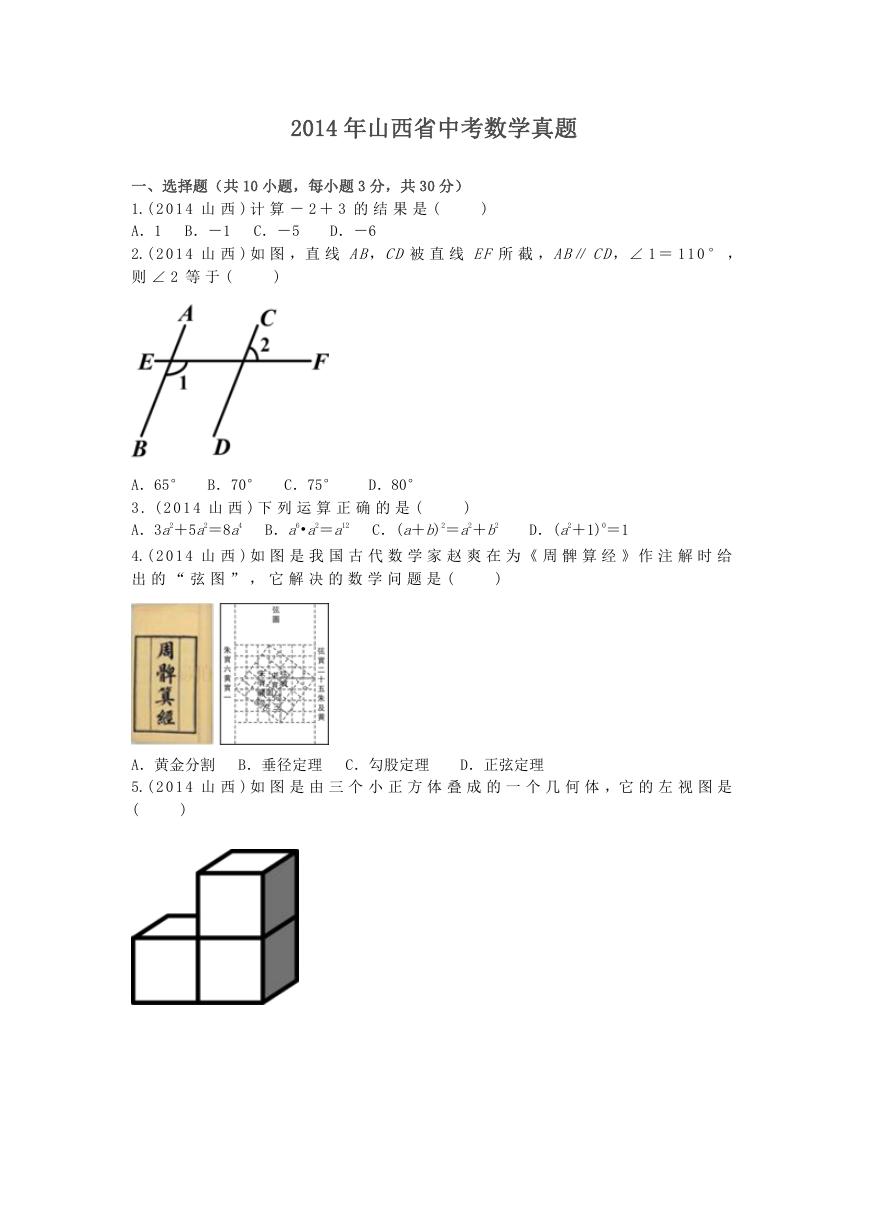
2014 年山西省中考数学真题一、选择题（共 10 小题，每小题 3 分，共 30 分） 1.( 2 0 1 4 山西 ) 计算－ 2 ＋ 3 的结果是 ( A．1 2.( 2 0 1 4 山西 ) 如图，直线 AB，CD 被直线 EF 所截，AB∥ CD，∠ 1 ＝ 1 1 0 ° ，则 ∠ 2 等于 ( B．－1 ) C．－5 D．－6 ) A．65° B．70° C．75° D．80° 3 . ( 2 0 1 4 山西 ) 下列运算正确的是 ( A．3a2＋5a2＝8a4 B．a6•a2＝a12 ) C．(a＋b)2＝a2＋b2 D．(a2＋1)0＝1 4.( 2 0 1 4 山西 ) 如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的 “ 弦图 ” ，它解决的数学问题是 ( ) A．黄金分割 B．垂径定理 C．勾股定理 5.( 2 0 1 4 山西 ) 如图是由三个小正方体叠成的一个几何体，它的左视图是 ( D．正弦定理 )

A． C． B． D． D．公理化 6 . ( 2 0 1 4 山西 ) 我们学习了一次函数、二次函数和反比例函数，回顾学习过程，都是按照列表、描点、连线得到函数的图象，然后根据函数的图象研究函数的性质，这种研究方法主要体现的数学思想是 ( A．演绎 B．数形结合 C．抽象 7.( 2 0 1 4 山西 ) 在大量重复试验中，关于随机事件发生的频率与概率，下列说法正确的是 ( A．频率就是概率 B．频率与试验次数无关 C．概率是随机的，与频率无关 D．随着试验次数的增加，频率一般会越来越接近概率 8.( 2 0 1 4 山西 ) 如图，⊙ O 是 △ ABC 的外接圆，连接 OA、OB，∠ OBA＝ 5 0 ° ，则 ∠ C 的度数为 ( ) ) ) D．80° A．30° B．40° C．50° 9 . ( 2 0 1 4 山西 )PM2 . 5 是指大气中直径小于或等于 2 . 5 μ m( 1 μ m＝ 0 . 0 0 0 0 0 1 m) 的颗粒物，也称为可入肺颗粒物，它们含有大量的有毒、有害物质，对人体健康和大气环境质量有很大危害．2 . 5 μ m 用科学记数法可表示为 ( A．2.5×10－5m B．0.25×10－7m C．2.5×10－6m D．25×10－5m )

10.( 2 0 1 4 山西 ) 如图，点 E 在正方形 ABCD 的对角线 AC 上，且 EC＝ 2AE，直角三角形 FEG 的两直角边 EF、EG 分别交 BC，DC 于点 M、N．若正方形 ABCD 的边长为 a，则重叠部分四边形 EMCN 的面积为 ( ) A． B． C． D．二、填空题（共 6 小题，每小题 3 分，共 18 分） 11.( 2 0 1 4 山西 ) 计算： 3a2b3 • 2 a2b＝ _ _ _ _ _ _ _ _ ． 12.( 2 0 1 4 山西 ) 化简的结果是 _ _ _ _ _ _ _ _ ． 13.( 2 0 1 4 山西 ) 如图，已知一次函数 y＝ kx－ 4 的图象与 x 轴， y 轴分别交于 A、 B 两点，与反比例函数在第一象限内的图象交于点 C，且 A 为 BC 的中点，则 k＝ _ _ _ _ _ _ _ _ ． 14.( 2 0 1 4 山西 ) 甲、乙、丙三位同学打乒乓球，想通过 “ 手心手背 ” 游戏来决定其中哪两个人先打，规则如下：三个人同时各用一只手随机出示手心或手背，若只有两个人手势相同 ( 都是手心或都是手背 ) ，则这两人先打，若三人手势相同，则重新决定．那么通过一次 “ 手心手背 ” 游戏能决定甲打乒乓球的概率是 _ _ _ _ _ _ _ _ ． 15.( 2 0 1 4 山西 ) 一走廊拐角的横截面如图所示，已知 AB⊥ BC， AB∥ DE， BC∥ FG，且两组平行墙壁间的走廊宽度都是 1 m，的圆心为 O，半径为 1 m，且 ∠ EOF＝ 9 0 ° ， DE， FG 分别与 ⊙ O 相切于 E， F 两点．若水平放

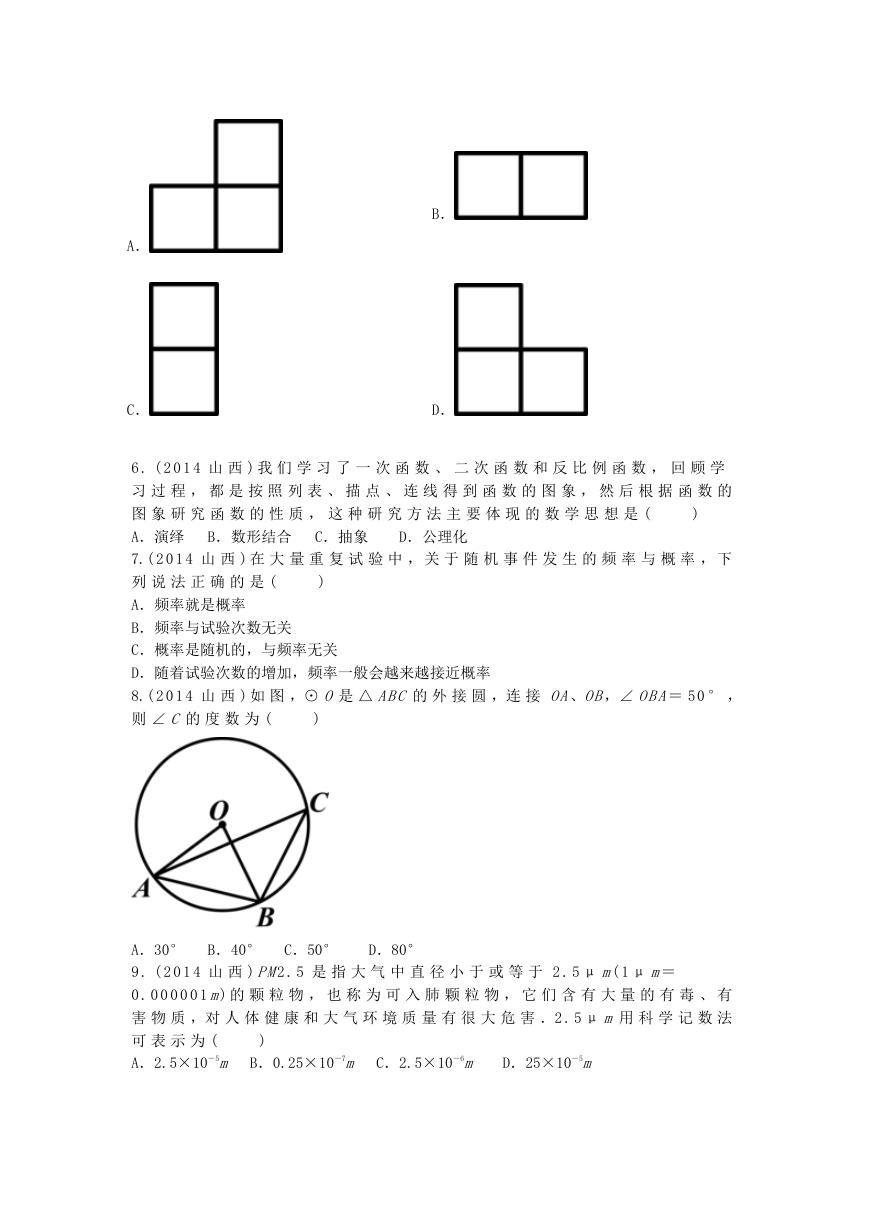
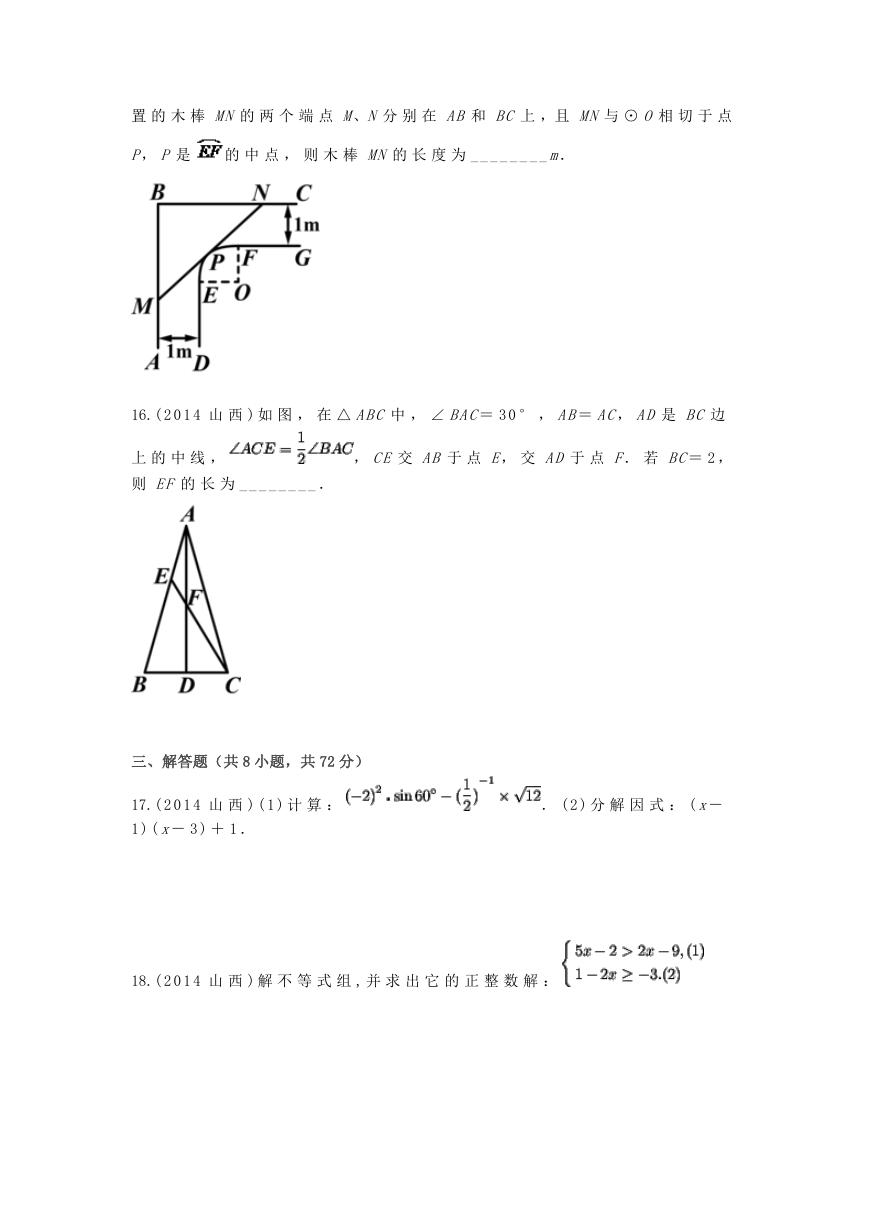
置的木棒 MN 的两个端点 M、N 分别在 AB 和 BC 上，且 MN 与 ⊙ O 相切于点 P， P 是的中点，则木棒 MN 的长度为 _ _ _ _ _ _ _ _ m． 16.( 2 0 1 4 山西 ) 如图，在 △ ABC 中， ∠ BAC＝ 3 0 ° ， AB＝ AC， AD 是 BC 边上的中线，， CE 交 AB 于点 E，交 AD 于点 F．若 BC＝ 2 ，则 EF 的长为 _ _ _ _ _ _ _ _ ．三、解答题（共 8 小题，共 72 分） 17.( 2 0 1 4 山西 ) ( 1 ) 计算：． ( 2 ) 分解因式： (x－ 1 ) ( x－ 3 ) ＋ 1 ． 18.( 2 0 1 4 山西 ) 解不等式组 , 并求出它的正整数解：

19.( 2 0 1 4 山西 ) 阅读以下材料，并按要求完成相应的任务．几何中，平行四边形、矩形、菱形、正方形和等腰梯形都是特殊的四边形，大家对于它们的性质都非常熟悉，生活中还有一种特殊的四边形——筝形．所谓筝形，它的形状与我们生活中风筝的骨架相似．定义：两组邻边分别相等的四边形，称之为筝形，如图，四边形 ABCD 是筝形，其中 AB＝AD， CB＝CD．判定：①两组邻边分别相等的四边形是筝形． ②有一条对角线垂直平分另一条对角线的四边形是筝形．显然，菱形是特殊的筝形，就一般筝形而言，它与菱形有许多相同点和不同点．如果只研究一般的筝形 ( 不包括菱形 ) ，请根据以上材料完成下列任务： ( 1 ) 请说出筝形和菱形的相同点和不同点各两条； ( 2 ) 请仿照图 1 的画法，在图 2 所示的 8 × 8 网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案，具体要求如下： ① 顶点都在格点上； ② 所设计的图案既是轴对称图形又是中心对称图形； ③ 将新图案中的四个筝形都图上阴影 ( 建议用一系列平行斜线表示阴影 ) ． 20.( 2 0 1 4 山西 ) 某公司招聘人才，对应聘者分别进行阅读能力、思维能力和表达能力三项测试，其中甲、乙两人的成绩如下表 ( 单位：分 ) ：

项目人员阅读思维表达甲乙 93 95 86 81 73 79 ( 1 ) 若根据三项测试的平均成绩在甲、乙两人中录用一人，那么谁将能被录用？ ( 2 ) 根据实际需要，公司将阅读、思维和表达能力三项测试得分按 3 ︰ 5 ︰ 2 的比确定每人的最后成绩，若按此成绩在甲、乙两人中录用一人，谁将被录用？ ( 3 ) 公司按照 ( 2 ) 中的成绩计算方法，将每位应聘者的最后成绩绘制成如图所示的频数分布直方图 ( 每组分数段均包含左端数值，不包含右端数值，如最右边一组分数 x 为： 8 5 ≤ x＜ 9 0 ) ，并决定由高分到低分录用 8 名员工，甲、乙两人能否被录用？请说明理由，并求出本次招聘人才的录用率． 21.( 2 0 1 4 山西 ) 如图，点 A、 B、 C 表示某旅游景区三个缆车站的位置，线段 AB， BC 表示连接缆车站的钢缆，已知 A、 B、 C 三点在同一铅直平面内，它们的海拔高度 AA′ ， BB′ ， CC′ 分别为 1 1 0 米、 3 1 0 米、 7 1 0 米，钢缆 AB 的坡度 i1 ＝ 1 ︰ 2 ，钢缆 BC 的坡度 i2 ＝ 1 ︰ 1 ，景区因改造缆车线路，需要从 A 到 C 直线架设一条钢缆，那么钢缆 AC 的长度是多少米？ ( 注：坡度 i 是指坡面的铅直高度与水平宽度的比 )

22.( 2 0 1 4 山西 ) 某新建火车站站前广场需要绿化的面积为 4 6 0 0 0 米 2 ，施工队在绿化了 2 2 0 0 0 米 2 后，将每天的工作量增加为原来的 1 . 5 倍，结果提前 4 天完成了该项绿化工程． ( 1 ) 该项绿化工程原计划每天完成多少米 2 ？ ( 2 ) 该项绿化工程中有一块长为 2 0 米，宽为 8 米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为 5 6 米 2 ，两块绿地之间及周边留有宽度相等的人行通道 ( 如图所示 ) ，问人行通道的宽度是多少米？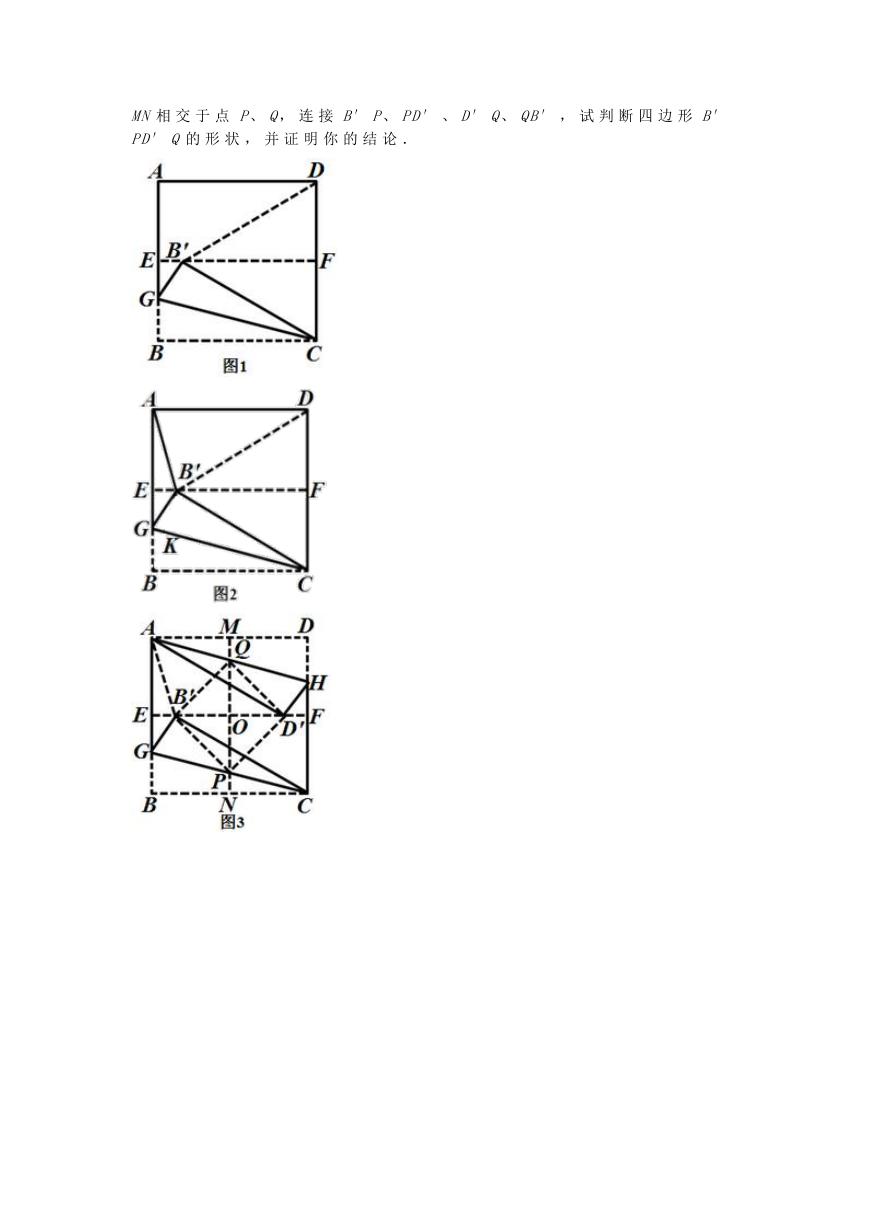 23.( 2 0 1 4 山西 ) 课程学习：正方形折纸中的数学．动手操作：如图 1 ，四边形 ABCD 是一张正方形纸片，先将正方形 ABCD 对折，使 BC 与 AD 重合，折痕为 EF，把这个正方形展平，然后沿直线 CG 折叠，使 B 点落在 EF 上，对应点为 B′ ．数学思考： ( 1 ) 求 ∠ CB′ F 的度数； ( 2 ) 如图 2 ，在图 1 的基础上，连接 AB′ ，试判断 ∠ B′ AE 与 ∠ GCB′ 的大小关系，并说明理由；解决问题： ( 3 ) 如图 3 ，按以下步骤进行操作：第一步：先将正方形 ABCD 对折，使 BC 与 AD 重合，折痕为 EF，把这个正方形展平，然后继续对折，使 AB 与 DC 重合，折痕为 MN，再把这个正方形展平，设 EF 和 MN 相交于点 O；第二步：沿直线 CG 折叠，使 B 点落在 EF 上，对应点为 B′ ，再沿直线 AH 折叠，使 D 点落在 EF 上，对应点为 D′ ；第三步：设 CG、 AH 分别与