基于遗传算法的MATLAB16阵元天线的优化.doc

发布时间：2022-06-16 发布人：admin 分类：说明书资料大小：0.14M 资料格式：doc 举报版权申诉

c4cbc660-42b9-4ec8-a7bf-e5eb9067ea39.doc.pdf-第1页.png

第1页 / 共12页

c4cbc660-42b9-4ec8-a7bf-e5eb9067ea39.doc.pdf-第2页.png

第2页 / 共12页

c4cbc660-42b9-4ec8-a7bf-e5eb9067ea39.doc.pdf-第3页.png

第3页 / 共12页

c4cbc660-42b9-4ec8-a7bf-e5eb9067ea39.doc.pdf-第4页.png

第4页 / 共12页

c4cbc660-42b9-4ec8-a7bf-e5eb9067ea39.doc.pdf-第5页.png

第5页 / 共12页

c4cbc660-42b9-4ec8-a7bf-e5eb9067ea39.doc.pdf-第6页.png

第6页 / 共12页

c4cbc660-42b9-4ec8-a7bf-e5eb9067ea39.doc.pdf-第7页.png

第7页 / 共12页

c4cbc660-42b9-4ec8-a7bf-e5eb9067ea39.doc.pdf-第8页.png

第8页 / 共12页

1 设计要求

2遗传算法

2.2 算法流程

2.3 选择

2.4交叉

2.5变异

3阵列天线原理

N元直线阵的阵因子函数

求增益

求旁瓣电平

4程序设计

5结果与讨论

6 参考文献

1 设计要求利用 Matlab 编制一个遗传算法或粒子群算法程序，并实现对间距为半波长均匀直线阵综合，指标如下：阵元数：16 元副瓣电平：<-30dB 增益：>11dB 要求撰写设计报告，内容包括：所采用的算法基本原理，目标函数的设计，各个参数的设置，源代码，仿真结果（增益方向图），参考文献。 2 遗传算法遗传算法的生物学基础自然选择学说认为适者生存，生物要存活下去，就必须进行生存斗争。生存斗争包括种内斗争、种间斗争以及生物跟环境之间的斗争三个方面。在生存斗争中，具有有利变异的个体容易存活下来，并且有更多的机会将有利变异传给后代，具有不利变异的个体就容易被淘汰，产生后代的机会就少得多。因此，凡是在生存斗争中获胜的个体都是对环境适应性比较强的个体。达尔文把这种生存斗争中适者生存，不适者淘汰的遗传算法(GA)是模拟生物在自然环境下的遗传和进化过程而形成的一种自适应全局优化概率搜索方法。其采纳了自然进化模型，从代表问题可能潜在解集的一个种群开始，种群由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体；初始种群产生后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的解：在每一代，概据问题域中个体的适应度大小挑选个体；并借助遗传算子进行组合交叉和主客观变异，产生出代表新的解集的种群。这一过程循环执行，直到满足优化准则为止。最后，末代个体经解码，生成近似最优解。基于种群进化机制的遗传算法如同自然界进化一样，后生代种群比前生代更加适应于环境，通过逐代进化，逼近最优解。

2.2 算法流程 2.3 选择指个体被选中并遗传到下一代群体中的概率与该个体的适应度大小成正 pi = fi / ( i=1,2,…,M ) fi 式中 pi——个体 i 被选中的概率； fi——个体 i 的适应度； fi——群体的累加适应度。显然，个体适应度愈高，被选中的概率愈大。但是，适应度小的个体也有比。可能被选中，以便增加下一代群体的多样性。执行概率选择的手段是轮盘选择。个体被选中的概率取决于个体的相对适应度：从统计意义讲，适应度大的个体，其刻度长，被选中的可能性大；反之，适应度小的个体被选中的可能性小，但有时也会被“破格”选中。 2.4 交叉 Ⅰ. 对群体中的个体进行两两随机配对。若群体大小为 M，则共有 [ M/2 ]对相互配对的个体组。 Ⅱ. 每一对相互配对的个体，随机设置某一基因座之后的位置为交叉点。若染色体的长度为 l ，则共有(l-1)个可能的交叉点位置。 Ⅲ. 对每一对相互配对的个体，依设定的交叉概率 pc 在其交叉点处相互交换两个个体的部分染色体，从而产生出两个新的个体。

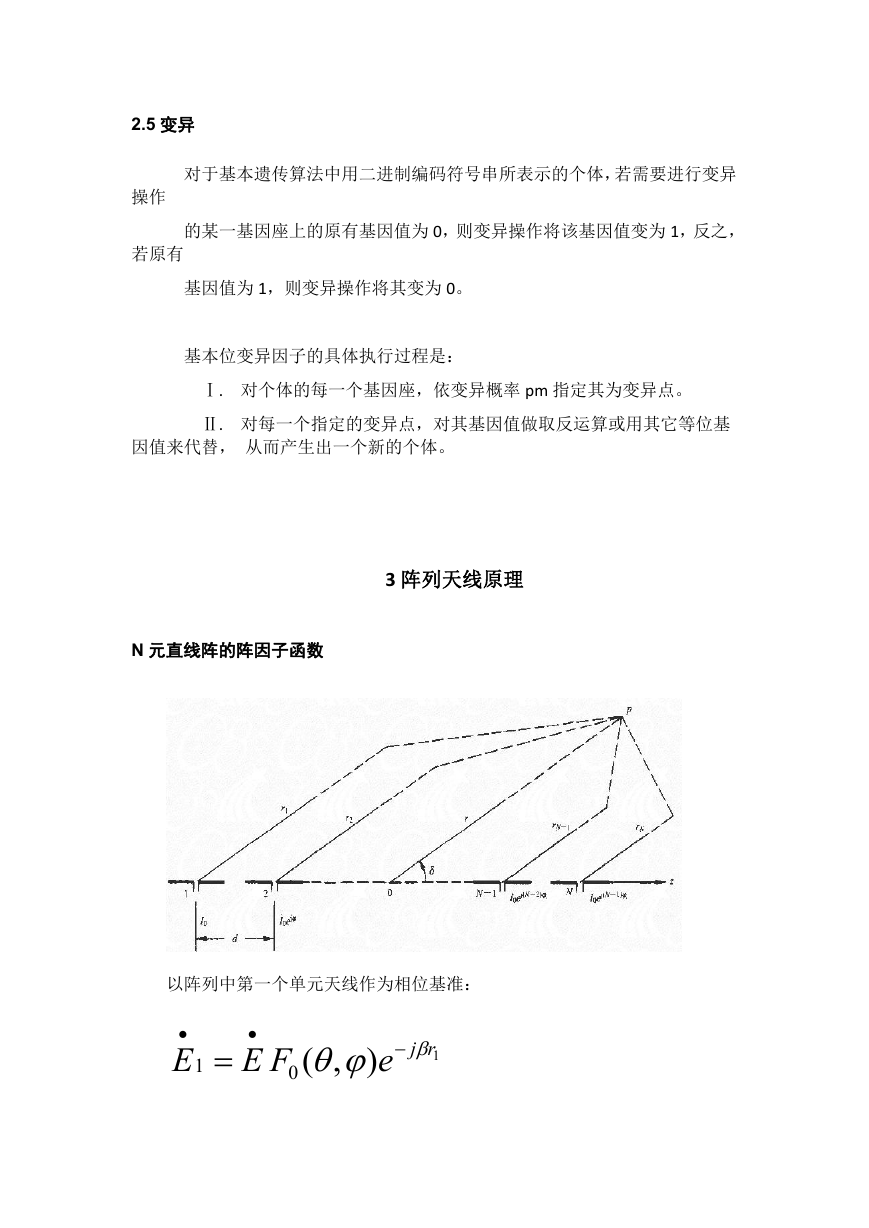
2.5 变异对于基本遗传算法中用二进制编码符号串所表示的个体，若需要进行变异的某一基因座上的原有基因值为 0，则变异操作将该基因值变为 1，反之，操作若原有基因值为 1，则变异操作将其变为 0。基本位变异因子的具体执行过程是： Ⅰ. 对个体的每一个基因座，依变异概率 pm 指定其为变异点。 Ⅱ. 对每一个指定的变异点，对其基因值做取反运算或用其它等位基因值来代替，从而产生出一个新的个体。 3 阵列天线原理 N 元直线阵的阵因子函数以阵列中第一个单元天线作为相位基准：  E 1   FE rje   ,(0 ) 1

第二个单元天线：辐射场的幅值差异不计，相位差为  d cos 则第 N 个单元天线的相位差为： ( N  )1   ( N  )(1 )  cos  d N 个相似元阵元在 p 处的辐射场叠加，表示为   FEE k 0  rj   ),( e 1 1[  e j   e j 2    e ( Nj   E  N  k  1  e 1[  e j  j 2    e ( Nj )1 ]     jN 1 e  1 e  j  1 Nj   2  e sin( sin( N  ) 2  ) 2 整理可得远区辐射场表达式为：  E   FE 0  ) ,(  sin( sin( N  ) 2  ) 2 ( 1 Nr     i 2 )  je       cos d 是相邻阵元至场点的辐射场总相位差由上式得 N 元均匀直线阵列的阵函数 F(δ)为

sin[ sin[ N  ] 2  ] 2  sin[ sin[ N 2 1 2 ( )]  cos  d ( )]  cos  d sin[ N  ] 2  sin[ ] 2 N  sin[  d cos N ( )]  2 1 sin[ 2 ( )]  cos  d N  sin[ N 2 1 sin[ 2 N F )(   f )(   求增益求旁瓣电平 4 程序设计 clear all; close all; clc; NP=50; %个体数 Pc = 0.8; %选择概率 Pm = 0.05; %变异概率 f=30000000;%信号频率

c=30000000; lamda = c/f;%波长 d = lamda/2;%间距 beta = 2*pi/lamda;%波数 seta0 = 0;%波束方向 G = 100; %最大遗传代数 L = 36; %编码数 NL = 16; %阵元数 NN = 1800; %划分刻度 E0 = 1; %电压电流 %%%生成初始种群 f = randint(NP,L); %产生一个 L*NP 的随机矩阵，正态分布 %初始种群的分布 maxE = 100; for i = 1:NP for j = 1:L if f(i,j)==1 plot(i,j) hold on end end end %%%%遗传算法循环 for k = 1:G k %解码，个体实际数 % 计算峰值旁瓣比，即适应度 for i = 1:NP F(i) = -MSLL3(d,beta,NN,NL,seta0,f(i,:),L,maxE); % 取成正的，下面方便取最大值并且处理 end% 取得 NP 个个体的旁瓣电平 maxF = max(F) minF = min(F) rr = find(F == maxF); fBest = f(rr(1),:); Fin = (F-minF)/(maxF-minF); %归一化 %rr(1,1) %fBest

%maxFit %%%基于轮赌盘的选择操作 sum_Fin = sum(Fin); fitvalue = Fin./sum_Fin; fitvalue = cumsum(fitvalue);%cumsum(A) 返回一个和 A 同行同列的矩阵， %矩阵中第 m 行第 n 列元素是 A 中第 1 行到第 m %行的所有第 n 列元素的累加和 ms = sort(rand(NP,1)); fiti = 1; newi = 1; while newi <= NP if(ms(newi)

end end end f = nf; f(1,:) = fBest; trace(k) = maxF; end figure plot(trace) xlabel('迭代次数') ylabel('目标函数值') title('适应度进化曲线') save fBestn.mat fBest save L.mat L save E.mat E0 %%%计算最大旁瓣%%% function MSLL3 = MSLL3(d,beta,NN,NL,seta0,f,L,maxE) seta = linspace(-pi,pi,NN); alfa = (2*pi*(f(1:L/2)*(2.^(0:L/2-1)'))/(2^(L/2)-1)); %解码 x = maxE/8*f(L/2+1:L)*(2.^(0:L/2-1)')/(2^(L/2)-1); %解码 I1 = linspace(maxE-(NL/2)*x,maxE,NL/2); I2 = linspace(maxE,maxE-(NL/2*x),NL/2); I = [I1,I2]-x; for m = 1:NN fai = beta*d*([0:NL-1]+1-(NL+1)/2)*cos(seta(m)-seta0)-[0:NL-1]*alfa; Fit(m) = abs(sum(I*exp(sqrt(-1)*(fai)'))); end %plot(alfa,fit) %hold on FdB = 20*log10(Fit/max(Fit)); %那如果需要找到其中满足一定条件的元素索引 %%%取旁瓣电平，即最大值之外的次大值 FdB = FdB-3;

分享到：

赞收藏

资料库

基于遗传算法的MATLAB16阵元天线的优化.doc

相关推荐

行业

热门标签

最新资料