论文研究-一种基于隐马尔可夫的软件可靠性监控方法 .pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.46M 资料格式：pdf 举报版权申诉

weixin_39841365-11572441-4744302543332839130.pdf-第1页.png

第1页 / 共9页

weixin_39841365-11572441-4744302543332839130.pdf-第2页.png

第2页 / 共9页

weixin_39841365-11572441-4744302543332839130.pdf-第3页.png

第3页 / 共9页

weixin_39841365-11572441-4744302543332839130.pdf-第4页.png

第4页 / 共9页

weixin_39841365-11572441-4744302543332839130.pdf-第5页.png

第5页 / 共9页

weixin_39841365-11572441-4744302543332839130.pdf-第6页.png

第6页 / 共9页

weixin_39841365-11572441-4744302543332839130.pdf-第7页.png

第7页 / 共9页

weixin_39841365-11572441-4744302543332839130.pdf-第8页.png

第8页 / 共9页

文本预览

中国科技论文在线 http://www.paper.edu.cn 一种基于隐马尔可夫的软件可靠性监控方法 周宇鹏 1，张鹏程 1，滕剑锋 1，李雯睿 2 (1. .河海大学计算机与信息学院,南京 211110； 2. 南京晓庄学院可信云计算与大数据分析重点实验室,南京 211171) 摘要：可靠性是众多软件系统的关键指标之一。针对构件式软件系统提出了一种对其可靠性进行监控的方法。对构件式系统中的每个构件，首先采集运行时数据对其进行隐马尔可夫模型建模，计算其单独可靠性；然后再对整个系统的运行时状态进行分析，再次映射到隐马尔可夫模型进行建模，计算整个系统的可靠性。实验表明，在构件式软件系统中，隐马尔可夫模型可以有效地反映系统的状态变化过程，基于隐马尔可夫模型的可靠性监控方法是可行的、有效的。关键词: 软件工程；软件自适应；可靠性监控；构件系统；隐马尔可夫模型中图法分类号：TP311 文献标识码：A Software reliability monitor method based on Hidden Markov Model Zhou Yupeng1, Zhang Pengcheng1, Ten Jianfeng1, Li Wenrui2 (1. School of Computer and Information, Hohai University, Nanjing 211110, China; (2. Key Laboratory for Credible Cloud Computing and Big Data Analyzing, Nanjing Xiaozhuang University, Nanjing 211100, China) Abstract: Reliability is an important property of software systems. Runtime reliability monitor can improve the quality of software system. Existing architecture-level reliability monitor approaches focus on system-level reliability and assume that the reliabilities of individual components are known. In general, this assumption is unreasonable, making component reliability monitor an important missing ingredient in the current literature. Considering the uncertainties of the runtime environment, reliability monitoring also faces lots of challenges. In this paper, we exploited a software monitor approach based on hidden markov model in a component-based system as a case. Key words: software engineering; self-adaptive software; reliability monitor; component-based system; hidden Markov model 可靠性评估是软件可靠性工程的核心内容之一，是通过软件系统的已有信息对系统可靠性进行有效评估和科学预测的技术方法的统称。可靠性评估的所得结果可用于指导软件结构的设计，并进一步验证软件是否符合设计要求。可靠性评估是运用计算机技术、人工智能、概率论知识等一系列测评手段对软件可靠性完成评估和预测的实践过程，由此可对影响软件可靠性的各种影响因素实施有效控制。目前，基于构件的软件技术正蓬勃发展，是对面向对象技术的进一步发展与改进。随着面向对象开发技术的逐渐普及，基于构件的软件开发方法也日益遍及各类应用。软件开发人员可以直接使用已有的构件，通过构件组装来完成系统的开发，既可以购买商用构件，也可以自行开发实现，因而每个构件的实现可能是完全异质的，由构件而组合开发的系统也不可避免地趋向于越发复杂。迄今为止，基于构件的软件开发技术还未成熟，仍然缺乏可用于构件及基于构件的软件非功能技术(可靠性、性能)实现的系统有效方法。如何确保软件的稳定质量，并准确评测基于构件的软件系统(简称构件式系统)的可靠性，仍将是一项投入巨大、且复杂的长期的艰巨任务[1-2]。传统的可靠性监控方法大多基于设计时(即在软件设计阶段)，根据软件体系结构来监控其可靠性，往往将软件中的各个构件的可靠性作为已知条件，不可避免地会将环境等运行时基金项目：国家自然科学基金资助项目(61202097)；高等学校博士学科点专项科研基金资助项目 (20120094120009) 作者简介：周宇鹏（1990—），男，硕士研究生，主要研究方向为自适应软件通信联系人：张鹏程，副教授，主要研究方向为软件工程，pchzhang@hhu.edu.cn -1-

中国科技论文在线 http://www.paper.edu.cn 的因素排除在外，从而带来不够“精确”的结果。相反地，运行时监控技术动态地根据实时数据对软件进行分析、监控，相对于设计时监控有着明显的优势。本文将讨论一种基于隐马尔可夫模型的可靠性监控方法。 1 相关工作在可靠性监控领域，已经有不少学者提出了各自的方法，随着时间的推移，原来的设计时监控方法大多都已经被运行时监控方法所取代。运行时监控与诊断技术，通过实时监测和分析目标系统的运行时状态和行为信息判断系统的运行时行为是否满足系统的属性规约，以发现系统的缺陷、异常，为软件系统的动态自适应调整和演化等活动提供决策依据，从而保证软件系统的安全可靠运行。规约语言规定了问题领域的需求和与系统行为相关的属性。监控器观察系统的行为与给定的属性规约是否一致。文献[3-4]通过计算成功样本与总样本的比值直接计算概率，然后与预定的概率标准比较，得出结论。这种基于估算的方法缺乏统计分析论证，与真实结果可能出现较大误差。文献[4]通过估算待监控系统属性的概率值，与属性规约预定义的概率标准进行比较，满足属性规约，则系统运行正常，反之，系统发生违例。文献[5][6]首先统计成功样本与总体样本的比值，然后利用假设检验根据一定的置信水平进行评估。文献[7]提出概率属性监控框架，针对运行时监控引入概率逻辑，用来定义概率属性并使用假设检验技术，尤其是 SPRT[8][8]，在显著性水平和 1情况下验证公式的正确性。文献[9]拓展 PSC[10]为 PTPSC 来表达概率属性规范，并定义相应的语义以及语义翻译器来自动生成结合 TBA 和 SPRT 程序的概率属性监控器。所有以 PTPSC 语言定义的特性都可以由该监控器监控分析。但是上述的假设检验方法不支持连续监控。随机过程可靠性模型是软件可靠性评估模型中的重要方法，也是当前软件可靠性增长模型领域研究最多、实际项目中应用最广泛的一类，在很多应用中都有良好的表现[11-12]。与上面的方法相比，它可以对更加复杂的系统属性进行有效监控和预测，但对数学模型的选择要求较高。随机过程可以描述随时间变化的软件失效行为，并具有“过程的将来行为仅依赖于现在的状态，而与其历史无关”的性质。随机过程模型的主要优点在于其模型的简单性，以及易于理解和实施[13]。在构件式系统中，通过软件体系结构定义的不同构件之间的交互代表了软件系统的行为。通过基于状态的方法来建立基于体系结构的可靠性模型，马尔可夫随机过程的应用是非常合适的[14-15]。隐马尔可夫模型在马尔可夫链的基础上又多了一层随机过程。在正常的马尔可夫模型中，状态对于观察者来说是直接可见的，状态的转换概率便是全部的参数。而在隐马尔可夫模型中，虽然状态并不是直接可见的，但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因为输出符号的序列能够透露出状态序列的一些信[16]息[16]，所以在构件式系统中，可以通过有效的抽象，将构建系统的状态转换关系映射到隐马尔可夫模型中，并利用已有的算法来计算需要的结果。随着移动互联网的兴起，智能家居的概念比以往有着更好的研究条件和前景。由于领域的特殊性，安全、可靠在智能家居领域有着更加严格的需求[17]。本文以一个智能家居系统为目标，对其软件构件进行建模，验证所提出的可靠性监控方法。 2 预备知识介绍 2.1 可靠性和失效定义本文中，可靠性定义为，在特定时间内、特定条件下系统执行其被设计的功能的概率 [18-20]。在嵌入式和移动软件系统中，如果系统的运行环境不断地在改变，其可靠性也可能会随着改变。失效是系统达到了一种偶然出现但是与其设定的规约不符的一种状态。错误可以由系统的硬件和软件缺陷所导致。反常的环境(内部环境、外部环境)会导致功能模块执行其规定功能的能力下降，所以失效是由于错误导致的[18-20]。 2.2 HMM 介绍隐马尔可夫模型可以被形式化地描述为一个五元组  -2-  S O A B π ( , , , , ) ，其中

中国科技论文在线 http://www.paper.edu.cn n , } S ) S A a ij O      为隐马尔可夫的隐含状态，n 表示隐含状态的总数；状态转移矩阵  表示各个隐含状态之间互相转移的概率，表示 t 时刻 HMM 模型由状态 Si 转移为 Sj 的概率；  为观测概率矩 S S S { , }n , ,  1 2 ija i j { , , 1, 2,  P x S x (  | t j t 1  O O O , { , , }m  为观测序列； 1 2 } { , , ,      n 为初始状态概率分布，即系统初始状态时处于各个隐含状态的概率， 1 2   更进一步有初始时刻  为系统处于某个状态的概率。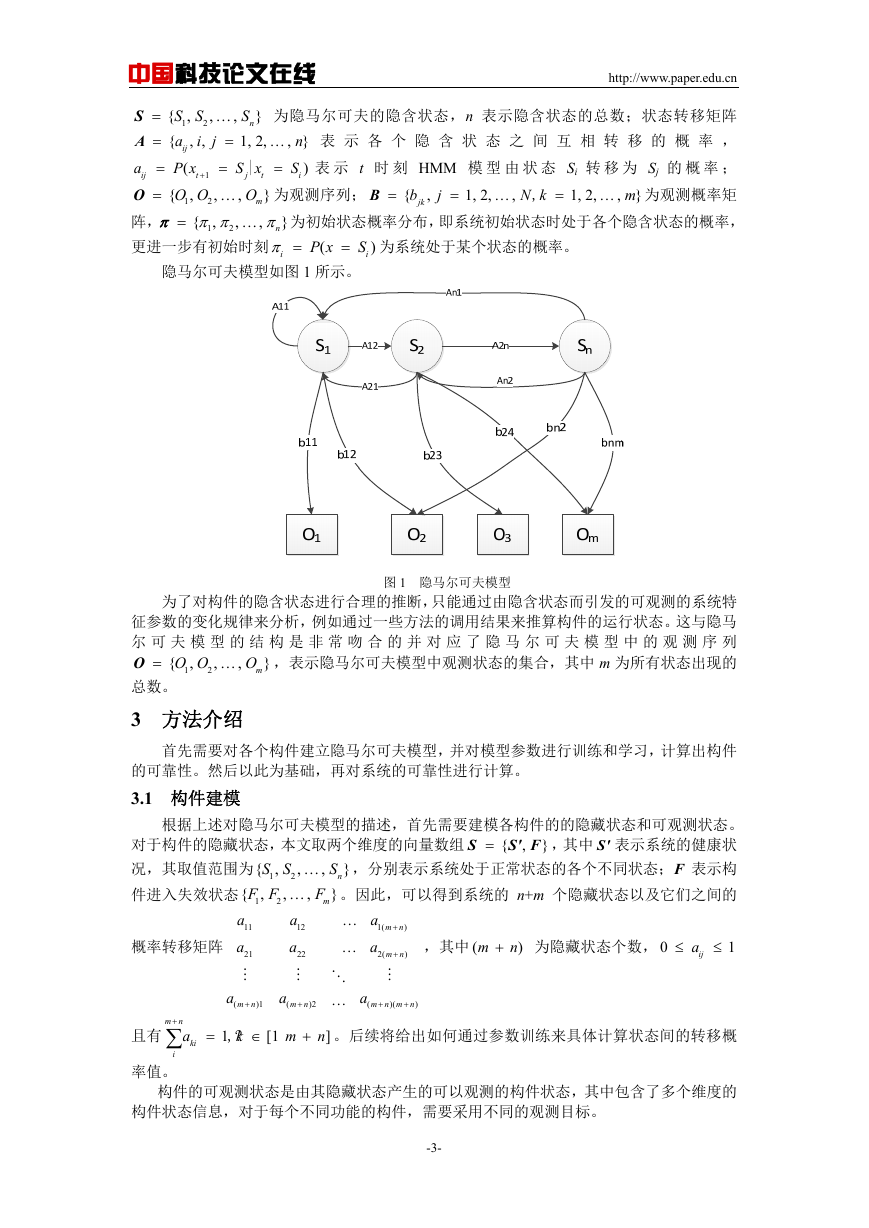 1, 2, 1, 2, N k , m , } jkb { 阵，   B    ) j , , i S i 隐马尔可夫模型如图 1 所示。 P x ( i 图 1 隐马尔可夫模型为了对构件的隐含状态进行合理的推断，只能通过由隐含状态而引发的可观测的系统特征参数的变化规律来分析，例如通过一些方法的调用结果来推算构件的运行状态。这与隐马尔可夫模型的结构是非常吻合的并对应了隐马尔可夫模型中的观测序列 O O O { , ，表示隐马尔可夫模型中观测状态的集合，其中 m 为所有状态出现的 1 2 总数。 3 方法介绍 O }m   , , 首先需要对各个构件建立隐马尔可夫模型，并对模型参数进行训练和学习，计算出构件的可靠性。然后以此为基础，再对系统的可靠性进行计算。 3.1 构件建模 S 根据上述对隐马尔可夫模型的描述，首先需要建模各构件的的隐藏状态和可观测状态。 S' F ，其中 S' 表示系统的健康状 { , }n ，分别表示系统处于正常状态的各个不同状态；F 表示构。因此，可以得到系统的 n+m 个隐藏状态以及它们之间的   对于构件的隐藏状态，本文取两个维度的向量数组 S S { , 况，其取值范围为 1 F F { , , 件进入失效状态 1 2 a 11 a 21  S , , 2 F , }m a 12 a 22  为隐藏状态个数， 0 概率转移矩阵，其中 ( m n a 1( a 2( ija m n   1  m n  } ) ) ) a ( m n  )1 a ( m n  )2 a ( m n m n  )(  )    k 1 ,?  [1 m n  ] 。后续将给出如何通过参数训练来具体计算状态间的转移概 m n  a ki 且有  i 率值。构件的可观测状态是由其隐藏状态产生的可以观测的构件状态，其中包含了多个维度的构件状态信息，对于每个不同功能的构件，需要采用不同的观测目标。 -3-

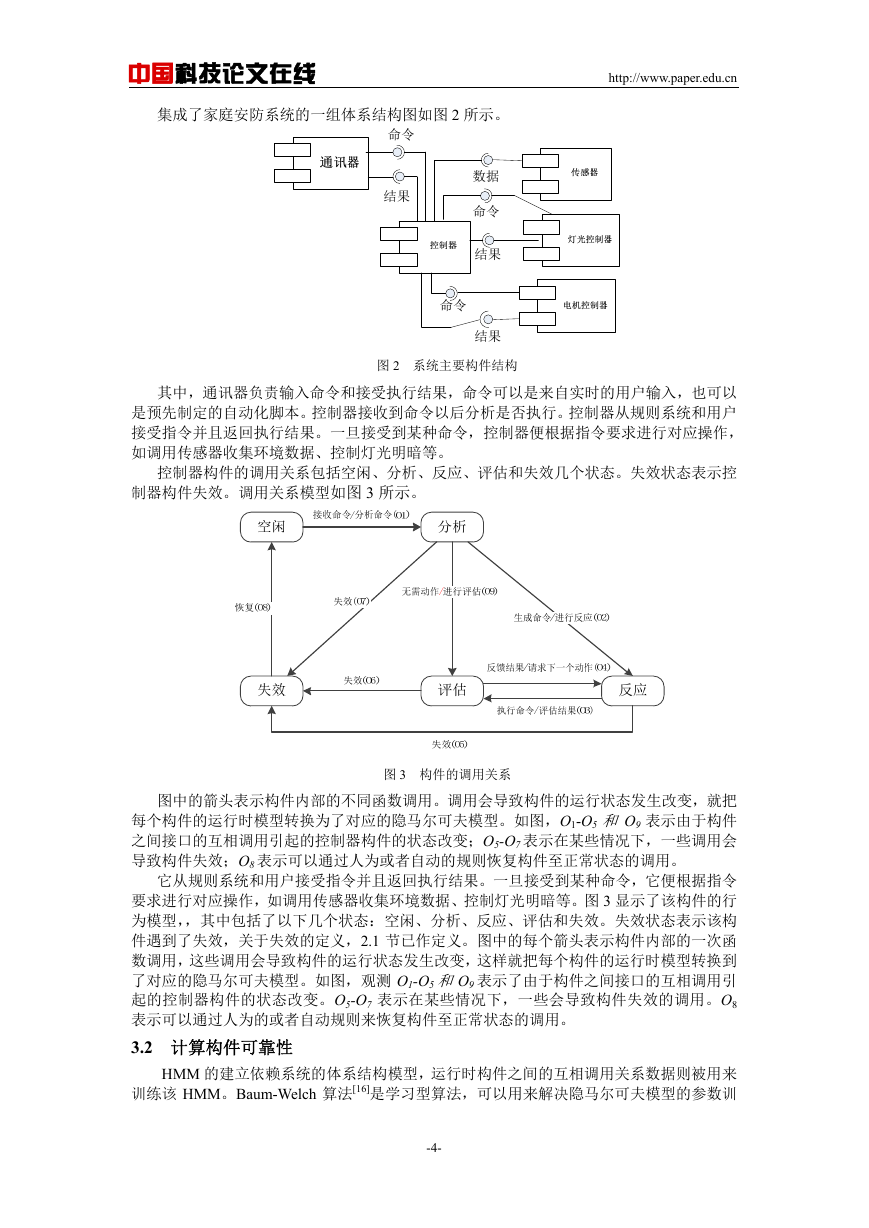
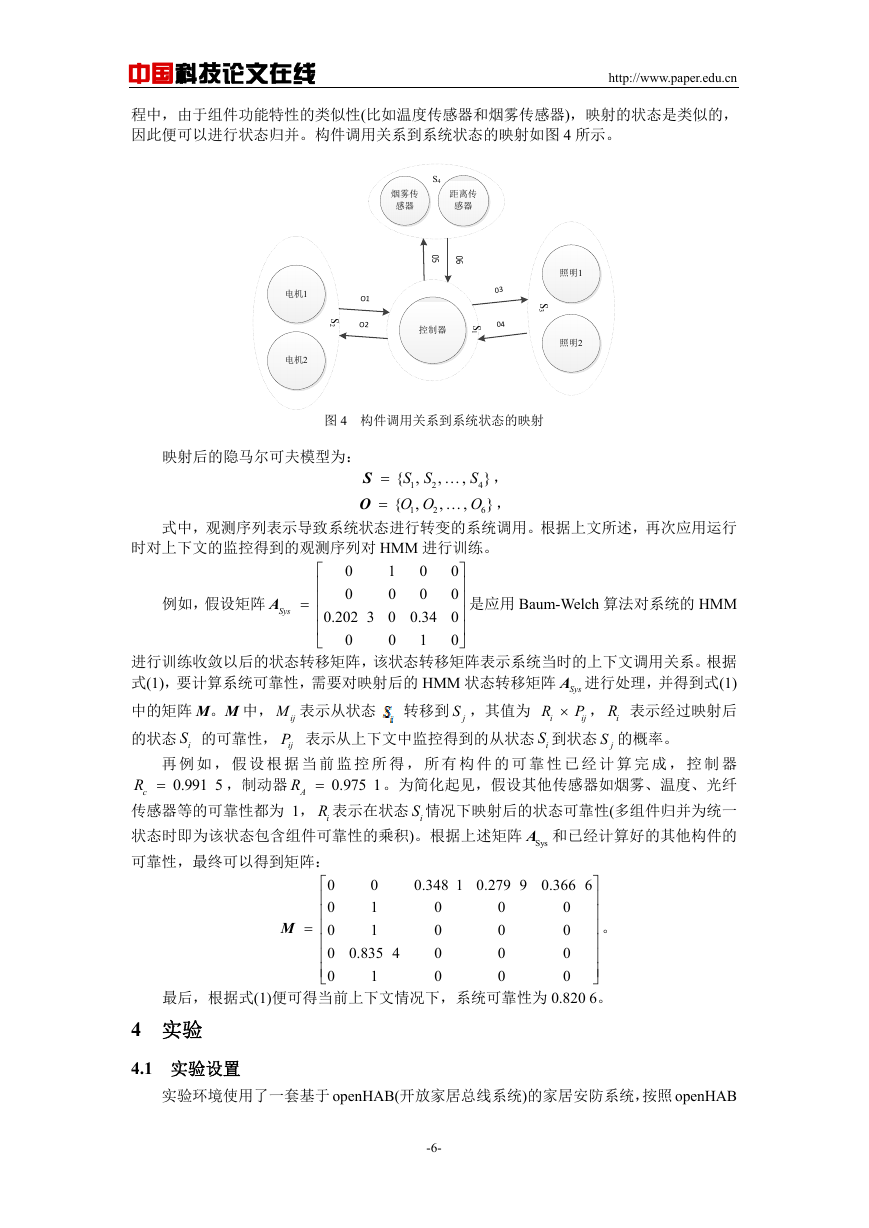
中国科技论文在线 http://www.paper.edu.cn 集成了家庭安防系统的一组体系结构图如图 2 所示。图 2 系统主要构件结构其中，通讯器负责输入命令和接受执行结果，命令可以是来自实时的用户输入，也可以是预先制定的自动化脚本。控制器接收到命令以后分析是否执行。控制器从规则系统和用户接受指令并且返回执行结果。一旦接受到某种命令，控制器便根据指令要求进行对应操作，如调用传感器收集环境数据、控制灯光明暗等。控制器构件的调用关系包括空闲、分析、反应、评估和失效几个状态。失效状态表示控制器构件失效。调用关系模型如图 3 所示。图 3 构件的调用关系图中的箭头表示构件内部的不同函数调用。调用会导致构件的运行状态发生改变，就把每个构件的运行时模型转换为了对应的隐马尔可夫模型。如图，O1-O5 和 O9 表示由于构件之间接口的互相调用引起的控制器构件的状态改变；O5-O7 表示在某些情况下，一些调用会导致构件失效；O8 表示可以通过人为或者自动的规则恢复构件至正常状态的调用。它从规则系统和用户接受指令并且返回执行结果。一旦接受到某种命令，它便根据指令要求进行对应操作，如调用传感器收集环境数据、控制灯光明暗等。图 3 显示了该构件的行为模型，，其中包括了以下几个状态：空闲、分析、反应、评估和失效。失效状态表示该构件遇到了失效，关于失效的定义，2.1 节已作定义。图中的每个箭头表示构件内部的一次函数调用，这些调用会导致构件的运行状态发生改变，这样就把每个构件的运行时模型转换到了对应的隐马尔可夫模型。如图，观测 O1-O5 和O9 表示了由于构件之间接口的互相调用引起的控制器构件的状态改变。O5-O7 表示在某些情况下，一些会导致构件失效的调用。O8 表示可以通过人为的或者自动规则来恢复构件至正常状态的调用。 3.2 计算构件可靠性 HMM 的建立依赖系统的体系结构模型，运行时构件之间的互相调用关系数据则被用来训练该 HMM。Baum-Welch 算法[16]是学习型算法，可以用来解决隐马尔可夫模型的参数训 -4-

中国科技论文在线 http://www.paper.edu.cn 练问题，得到 HMM 拟合后的状态转移矩阵 A。训练数据是由连续的观测序列组成，给定一个如上文所述的已初始化的 HMM 模型，Baum-Welch 算法应用输入数据对 HMM 的状态转移矩阵 A 进行训练，使其收敛。本文运用该算法，将从系统运行时上下文得到的监控数据用于构件和系统的 HMM 模型训练。如上文和图 2 所描述，构件的状态集合 S' 和观测序列 O 由该构件的行为模型所定义。如对于系统中的控制器来说，可以获得以下集合： , 3  S' S S S S S ， } { , , 1 2 O O O { , ，  1 2 , 4 O , 9 f } , 式中，状态 1S 表示空闲， fS 表示失效状态；观测序列 O1、O2、 、O10 对应于状态之间的转移。如图 2 所示，运行时，观测序列是以构件的执行轨迹的形式存在的，所以通过监控得到构件的执行轨迹，即可得到运行时构件的观测序列。考虑已由 Baum-Welch 算法基于运行时观测数据训练好的状态转移矩阵 0 0.23 0.049 0 1 0 0 0 0 0.32 0 0.87 A C          0 0 0.496 0.068 0.947 0.004 0.13 0 0 ，要计算运行时构件的可靠性，需要获得 AC 矩阵         0.043 0.34 0.077 0.546 的平稳状态向量，通过该向量可以计算得出构件不在 fS 状态的概率。平稳状态表示马尔可夫模型中的一个随机现象在某个特定状态的概率[15]，则上述矩阵 A 的平稳状态向量为： [0.169 8 0.108 3 0.238 1 0.352 1 0.131 7] 。上述向量的最后一列表示构件处于失效状态的概率，则基于当前的上下文环境，该构件的可靠性为： cR  1  0.131 7  0.868 3 。 3.3 计算系统可靠性一旦得到了所有构件的可靠性，便可以分析系统的可靠性。本文基于马尔可夫模型的配置层面的可靠性分析方法基于文献[12]中提出的模型。文献[12]中，系统的可靠性分析依赖于独立的各构件，以及决定构件之间交互的体系结构和系统运行时的上下文环境。构件和构件之间的交互被映射到了 DTMC(离散时间马尔可夫链)的状态图上，在并发状态情况下，根据控制流可将一个状态 iS 映射为一个或多个构件。一个状态转移概率 ijP 表示状态从 iS 转移到 jS 的概率。所以，系统可靠性 R 计算公式为： E  (1) I M ( 1)k   R k R  1 式中，M 是一个 k 行列式的值；E 是矩阵 ( k 的矩阵； 1S 是进入状态； kS 是退出状态； I M 是矩阵 ( I M 的 I M 排除最后一行和第一列后的行列式的值。M 中每个元素为： ) )  M i,j   RP   i ij  0? 状态S到状态S 且i j  i j 否则式中， iR 是状态 iS 的可靠性； kR 是退出状态的可靠性。该模型需要从运行时上下文中使用的相关信息来得出特定配置情况下相关系统的可靠性数值，尤其是需要状态之间的转移概率。如上文所述，系统运行时的状态转移概率依赖于运行时的上下文环境。因此，可以将 DTMC 转化为一个 HMM，通过运行时监控上下文来得到观测序列，进而再次使用 Baum-Welch 算法来训练该 HMM，从而得到转移矩阵等价于上述 DTMC 中的 M。根据图 2 和图 3 所示，观测序列依旧是系统运行时监控的上下文。在系统的实际运行过 -5-

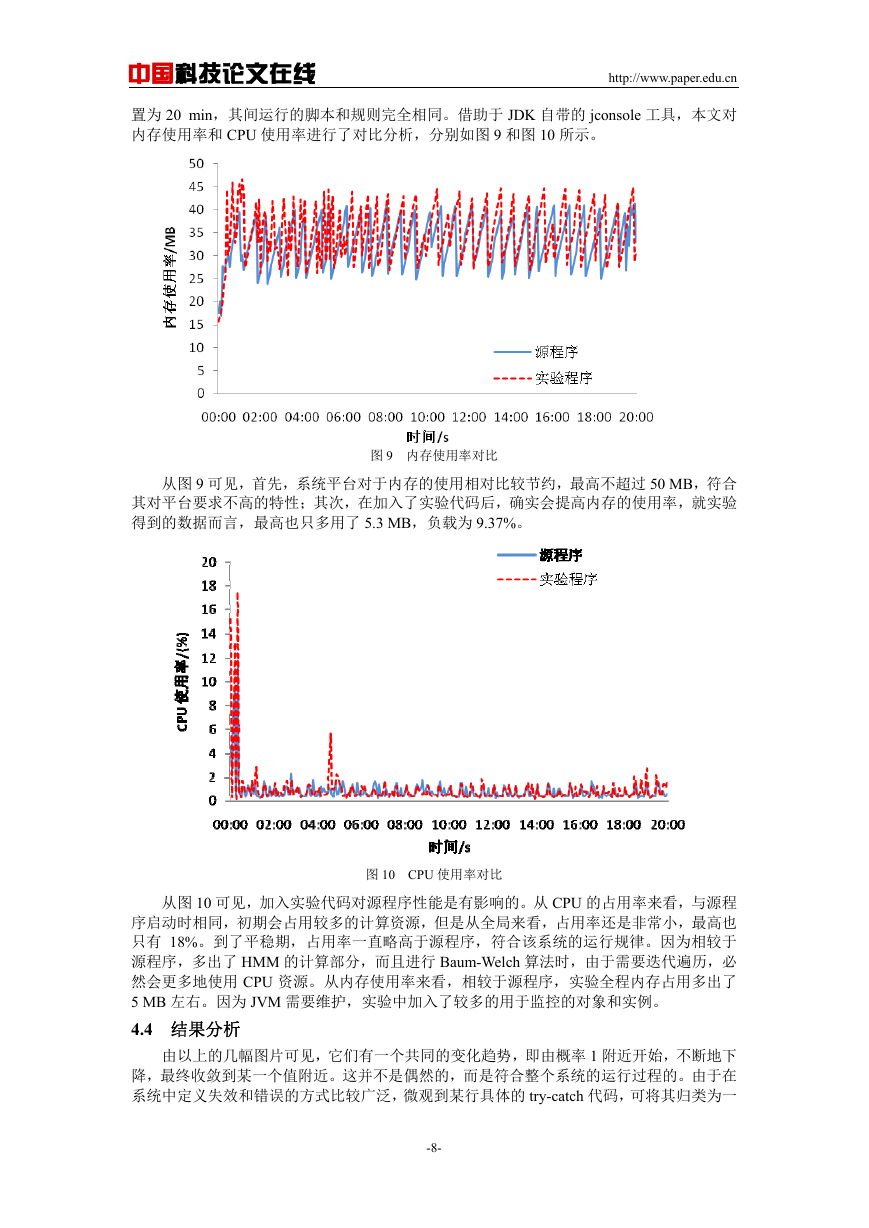
中国科技论文在线 http://www.paper.edu.cn 程中，由于组件功能特性的类似性(比如温度传感器和烟雾传感器)，映射的状态是类似的，因此便可以进行状态归并。构件调用关系到系统状态的映射如图 4 所示。 S4 烟雾传感器距离传感器 O1 O2 控制器 03 0 4 电机1 电机2 图 4 构件调用关系到系统状态的映射映射后的隐马尔可夫模型为： S O   S S { , 1 2 O O { , 1 2 , ,   , , S 4 O 6 } ， } ，照明1 照明2 式中，观测序列表示导致系统状态进行转变的系统调用。根据上文所述，再次应用运行时对上下文的监控得到的观测序列对 HMM 进行训练。例如，假设矩阵 A Sys        0 0 0 0 1 0 0 0 0.202 3 0 0.34 0 0 0 0 1 是应用 Baum-Welch 算法对系统的 HMM       进行训练收敛以后的状态转移矩阵，该状态转移矩阵表示系统当时的上下文调用关系。根据式(1)，要计算系统可靠性，需要对映射后的 HMM 状态转移矩阵 SysA 进行处理，并得到式(1) P ， iR 表示经过映射后中的矩阵 M。M 中， ijM 表示从状态转移到 jS ，其值为的状态 iS 的可靠性， ijP 表示从上下文中监控得到的从状态 iS 到状态 jS 的概率。 R i ij AR  0.975 1 0.991 5 ，制动器再例如，假设根据当前监控所得，所有构件的可靠性已经计算完成，控制器 cR  。为简化起见，假设其他传感器如烟雾、温度、光纤传感器等的可靠性都为 1， iR 表示在状态 iS 情况下映射后的状态可靠性(多组件归并为统一状态时即为该状态包含组件可靠性的乘积)。根据上述矩阵 SysA 和已经计算好的其他构件的可靠性，最终可以得到矩阵： 0   0   0  0 0.835 4   0  0.348 1 0.279 9 0.366 6 0 0 0 0 0 0 0 0 0 0 0 0         0 1 1 1 M  。最后，根据式(1)便可得当前上下文情况下，系统可靠性为 0.820 6。 4 实验 4.1 实验设置实验环境使用了一套基于 openHAB(开放家居总线系统)的家居安防系统，按照 openHAB -6-

中国科技论文在线 http://www.paper.edu.cn 提供的规则和脚本功能，编写了控制规则和安防脚本，再加入照明、电机和传感器的绑定来模拟家居安防系统的实验场景。在对源码进行了完整的分析以后，便可以得知每个构件内部的运行关系和系统的状态转移关系，接下来便可以将每个构件和整个系统的调用关系映射到它们对应的隐马尔可夫模型中。实验所用的操作系统为 windows8.1 32 位企业版，处理器为 Intel(R) Core(TM) i3-2120 CPU @ 双核 3.30 GHz，运行内存 4 GB，Eclipse Java EE IDE，Luna Release (4.4.0)，安装 Maven、AspectJ 相关插件。openHAB 是基于 OSGi 的应用，Equinox 是本文项目中用到的 OSGi 实现，为了对各个方法的调用进行监控，项目中使用了 AspectJ 相关开发包。 4.2 实验结果每隔 5 s 将监控得到系统调用结果作为 Baum-Welch 算法的输入，运行一段时间以后，收集到总共 86 组数据，通过它们计算得到矩阵 A，再通过 A 计算最终的系统可靠性。在系统中，传感器由于只有单向数据流，其可靠性只能参照其说明手册中的值，本文试验中假设为恒定值 0.95。由于计算方法相同，只列出了灯光控制器、电机控制器、控制器和系统的可靠性实验结果，分别如图 5、图 6、图 7 和图 8 所示。图 5 控制器可靠性图 6 电机控制器可靠性图 7 灯光控制器可靠性图 8 系统可靠性从以上 4 幅图可见，各构件的可靠性都是从 1 开始不断下降，中间会出现波动，直至收敛到某个值附近。由于各个构件的调用关系比较复杂，导致进入错误状态的系统调用占总调用次数的比例也在不断波动，间接地导致了可靠性的波动。从图 8 中可以发现，系统可靠性曲线的变化趋势明显地与其他构件的可靠性曲线的变化趋势相似，符合系统的运行状态和运行规律。 4.3 性能测试为了测试实验代码对源程序本身性能的影响，实验中加入了性能测试部分。测试方法为在指定时间内，在相同的外部环境情况下，加入实验代码的程序和源程序的 CPU 使用率、堆内存占用率。测试时间从程序加载开始到平稳运行的指定时间截止。根据经验判断，在程序启动 2 min 后，已经开始平稳运行。由于实验使用了家居安防的一些场景，将测试时间设 -7-

中国科技论文在线 http://www.paper.edu.cn 置为 20 min，其间运行的脚本和规则完全相同。借助于 JDK 自带的 jconsole 工具，本文对内存使用率和 CPU 使用率进行了对比分析，分别如图 9 和图 10 所示。图 9 内存使用率对比从图 9 可见，首先，系统平台对于内存的使用相对比较节约，最高不超过 50 MB，符合其对平台要求不高的特性；其次，在加入了实验代码后，确实会提高内存的使用率，就实验得到的数据而言，最高也只多用了 5.3 MB，负载为 9.37%。图 10 CPU 使用率对比从图 10 可见，加入实验代码对源程序性能是有影响的。从 CPU 的占用率来看，与源程序启动时相同，初期会占用较多的计算资源，但是从全局来看，占用率还是非常小，最高也只有 18%。到了平稳期，占用率一直略高于源程序，符合该系统的运行规律。因为相较于源程序，多出了 HMM 的计算部分，而且进行 Baum-Welch 算法时，由于需要迭代遍历，必然会更多地使用 CPU 资源。从内存使用率来看，相较于源程序，实验全程内存占用多出了 5 MB 左右。因为 JVM 需要维护，实验中加入了较多的用于监控的对象和实例。 4.4 结果分析由以上的几幅图片可见，它们有一个共同的变化趋势，即由概率 1 附近开始，不断地下降，最终收敛到某一个值附近。这并不是偶然的，而是符合整个系统的运行过程的。由于在系统中定义失效和错误的方式比较广泛，微观到某行具体的 try-catch 代码，可将其归类为一 -8-

分享到：

赞收藏

资料库

论文研究-一种基于隐马尔可夫的软件可靠性监控方法 .pdf

相关推荐

开发技术

热门标签

最新资料