CHINESE JOURNAL OF MECHANICAL ENGINEERING Vol. 20,aNo. 2,a2007 ·104· ZHANG Xinming HE Yongyong HAO Rujiang CHU Fulei State Key Laboratory of Tribology, Tsinghua University, Beijng 100084, China 0 INTRODUCTION PARAMETERS OPTIMIZATION OF CONTINUOUS WAVELET TRANSFORM AND ITS APPLICATION IN ACOUSTIC EMISSION SIGNAL ANALYSIS OF ROLLING BEARING* Abstract: Morlet wavelet is suitable to extract the impulse components of mechanical fault signals. And thus its continuous wavelet transform (CWT) has been successfully used in the field of fault diagnosis. The principle of scale selection in CWT is discussed. Based on genetic algorithm, an opti- mization strategy for the waveform parameters of the mother wavelet is proposed with wavelet en- tropy as the optimization target. Based on the optimized waveform parameters, the wavelet scalogram is used to analyze the simulated acoustic emission (AE) signal and real AE signal of rolling bearing. The results indicate that the proposed method is useful and efficient to improve the quality of CWT. Key words: Rolling bearing Fault diagnosis Acoustic emission (AE) Continuous wavelet transform (CWT) Genetic algorithm Rolling element bearings are of great importance to almost all forms of rotating machinery. Therefore, bearing failure (e.g. cracking, spalling) is one of the foremost causes of breakdown in rotating equipments. As a consequence, the condition monitoring and fault diagnosis of rolling element bearings are very important. For rolling element bearings, the most widely used detection methods are based on vibration signals. Several techniques have been applied to analyze vibration signals. However, the vibration signals may be interfered by other sources, and are not sensitive to the incipient fault, which make it difficult to detect the defect in early stage. Acoustic emission technique (AET) is a kind of dynamic non-destructive technique, developed in 1960s. Particles inside martial (atoms, molecules and particle swarm) will generate elastic waves from the transient release of strain energy as a result of the relative motion. These elastic waves are defined as acoustic emission (AE), which can be used to understand and detect the subsurface condition of material[1]. When the rolling bearing with defects is under operation, the defect (surface de- fect, cracking or spalling) will generate elastic impact between the contact surfaces, and give birth to AE. The AE involves abundant rubbing information and can be used for the condition monitoring and fault diagnosis of rolling bearing. Different from the vibration signals, AE signals always have a high frequency rang (above 20 kHz). So AEs can not be interfered by other me- chanical vibrations. And that AE are sensitive to early fault. All of these characteristics make AE methods be of great suitability and preponderance for the condition monitoring and fault diag- nosis of rolling bearing. As vibration signals, AEs of rolling bearing are also non-stationary and non-linear signals. So it’s efficient to analyze AEs with wavelet transform. Morlet wavelet has similar wave shape to the impulse component in the mechanical fault signals [2]. Thus it’s suitable to extract the impact feature of the defect[2-3]. Continuous wavelet transform (CWT) of Morlet has found wide- spread application in mechanical fault diagnosis[2-4], while the time-frequency transform performance is affected by parameters * This project is supported by National Natural Science Foundation of China (No. 50105007) and Program for New Century Excellent Talents in Uni- versity, China. Received March 21, 2006; received in revised form Sep- tember 14, 2006; accepted October 8, 2006 selection. However, how to select the parameters in order to opti- mize the transform performance is still lack of systematic study, so far the parameters are generally selected by experience[5-6]. The parameters selection in Morlet CWT is discussed in detail, and a principle of scale selection is discussed. Based on genetic algo- rithm, an optimization strategy for the waveform parameters of the basic wavelet is proposed. Applying this optimization to the analysis of rolling bearing AE signals can extract its time-fre- quency feature, also can develop the AET method for rolling bearing condition monitoring and fault diagnosis. 1 CONTINUOUS WAVELET TRANSFORM Let x(t) be a squared integrabel function, i.e. x(t) ∈ L2(R), the CWT of this function is defined as the integral transform with a function family ψa,τ(t) as the integral kernel[5], shown as follows WT a ( , ) τ x = −∞ +∞ ∫ 1 a x t ( ), < x t ( ) * ψ ψ a t ( )τ , d t = t τ −⎛ ⎞ ⎜ ⎟ a ⎝ ⎠ > (1) where ψa,τ(t) is generated by dilation and translation from the mother wavelet ψ(t) shown as follows t τ −⎛ ⎞ ψ ⎟ ⎜ a ⎠ ⎝ 1 a (2) ψ a t ( ) = , τ where a is a scale fatcor (in real engineering application, only a>0 is discussed), and τ is time location. The factor a–1/2 is used to ensure energy preservation. There can be several selections of mother wavelet ψ(t), but it should satisfy the admissibility condi- tion and its time-domain should be compact-support. Compared with discrete wavelet transform (DWT), CWT has such advantages: The wavelet needn’t to be orthogonal and is of time invariant; The sampling grids in the time-scale plane are less sparse. These advantages make CWT more suitable for fea- ture extraction in mechanical fault signals[2]. However, the time-frequency transform performance is depended upon the se- lection of mother wavelet. The principle of this selection is to make the wave shape of the mother wavelet more similar with the analyzed signal. And wavelet entropy can reflect such similarity. Ref. [2] proposed the selection method of mother wavelet based on wavelet entropy, in order to analyze vibration signal. And the selection of the shape parameter β of Morlet wavelet is optimized. Based on the wavelet entropy principle, Ref. [3] discussed the 

CHINESE JOURNAL OF MECHANICAL ENGINEERING ·105· wavelet transform performance of typical AE signals. After com- paring the transform results of Morlet wavelet, DB1-DB10 wave- let, Meyer wavelet and Sym1-Sym4 wavelet, Ref. [3] concluded that the Morlet wavelet is most suitable for the analysis of AE signals. In this paper, for the purpose of analyzing AE signals, the selection of wave shape parameter of Morlet wavelet is discussed more systematically, and an optimization strategy based on ge- netic algorithm is proposed. When used to analyze real signals, Morlet wavelet is defined as From above it can be seen that: β and ω0 balance the time-frequency resolution. For different signals, different parame- ters should be selected for better performance. According to Eq. (4), π (Hz), the half-power band width of Morlet wavelet is the central frequency is f0 ( f0=ω0/(2π)). Hence, the quality factor Q (central frequency/band width) can be defined as /(2 ln 2 ), β i.e. β and ω0 determine the quality factor of Morlet wavelet. And thus, wavelet analysis quality is optimized simultaneously when these two parameters are optimized. ln 2 / ω 0 β ψ t ( ) ⎛ ⎜ ⎝ Its Fourier transform is exp = − t 2 2 β 2 ⎞ ⎟ ⎠ cos( ω β ) t 0 > 0 (3) 2 PARAMETERS OPTIMIZATION OF MORLET WAVELET TRANSFORM ˆ( ) ψω = / 2 π β exp ⎡ ⎢ ⎢ ⎣ ⎛ −⎜ ⎝ − ω ω 0 2 β 2 ⎞ ⎟ ⎠ ⎤ ⎥ ⎥ ⎦ (4) Strictly speaking, Morlet wavelet doesn’t satisfy the admissi- bility condition[5], for ˆ( ψω = 0) = ( π/2 / β )exp( ω β2 − / 2 2 0 ) ≠ 0 (5) However, when ω0/β≥5, it can approximately satisfy it. Parameter β and central frequency ω0 control the shape of basic Morlet wavelet: When ω0 is fixed, the increase of β will accelerate the attenuation of basic wavelet, and decrease the sup- port domain of the wave shape, as shown in Fig. 1. Fig. 1 Wave shape of basic Morlet wavelet with different β When β tends to infinity, basic wavelet becomes a Dirac func- tion, which has the finest time resolution while no frequency resolu- tion; When β tends to 0, basic wavelet becomes a cosine function, which has the finest frequency resolution while no time resolution. When β is fixed, ω0 controls the oscillating frequency on time sup- port domain; increase of ω0 will accelerate the oscillation of basic wavelet, as shown in Fig. 2. On the other hand, when used to ana- lyze the same frequency component, increase (decrease) Morlet wavelet central frequency ω0, will make the frequency resolution higher (lower), while time resolution lower (higher)[7]. 2.1 Scale selection Generally, the frequency corresponding to the scale a is called pseudo-frequency, the relation between pseudofrequency (fa) and central frequency (f0) is [8]: fa=f0 fs /a. As the quality factor (Q) of wavelet is constant, the half-power frequency band width corresponding to scale a is a . Thus the upper and ) ln 2 /( π fH=fa+βfs fL=fa– cut-off frequency lower a , respectively. On the principle of sampling fre- f ) π β quency, if the upper cut-off frequency exceeds the limit of ana- lyzed signal, this analysis will be meaningless[7], i.e. fH≤fs / 2 should be satisfied. As a consequence, the least scale can be de- termined as a a f β = π + f β s are ( ω β ln 2 /(2 ln 2 /(2 ln 2) / ln 2) / ),aπ (6) π = π + ( s 0 min 0 On the other hand, according to the characteristic and fre- quency spectrum of AE signal of rolling bearing, it is known that the frequency range of which is above 20 kHz. Those, whose fre- quency is lower than 20 kHz, can be treated as noise, i.e. the lower limit of wavelet frequency band width should satisfy: fL≥ 20 000, and the largest scale is a max = f s ( ω β0 − 40 000 ln 2) π (7) The largest scale should also guarantee the time domain resolution[7]. For Morlet wavelet, a≤sigLen/6 should be satisfied, where sigLen stands for the length of analyze signal. 2.2 Selection of Morlet wavelet parameter β and central frequency based on wavelet entropy 2.2.1 Wavelet entropy After wavelet transform, define the wavelet energy on each single scale as E j = ∫ WT j τ τ 2( , )d x Then the total energy on scale-time plane can be described as E E T = ∑ j j (8) (9) Define the relative energy on each scale as Then the wavelet entropy can be defined as [3] Pj =Ej /ET P P lnj j = −∑ W E j (10) (11) Fig. 2 Wave shape of basic Morlet wavelet with different ω0 When selecting a proper basic wavelet, almost every element of the transform coefficient matrix is 0, except those scales that contain the frequency component of the analyzed signal. Thus the sparsity of the transform matrix can be used to evaluate the se- lected basic wavelet. If the coefficient matrix is treated as a pro- bability distribution serial, its wavelet entropy reflects its sparsity, i.e. the basic wavelet, which has the least wavelet entropy, is the best one. Hence Morlet wavelet parameters can be optimized with 

·106· ZHANG Xinming, et al: Parameters optimization of continuous wavelet transform and its application YZHANG Xinming, et al: Parameters optimization of continuous wavelet transform and its application in acoustic Y in acoustic emission signal analysis of rolling bearing wavelet entropy as the selection criterion. Least wavelet entropy means most similar to the feature of the analyzed signal. Fig. 3 is the wavelet entropy on ω0-β plane, from a simula- tion signal after wavelet transform. Where 20 points are selected uniformly between [1, 20] for ω0, and 100 points are selected uniformly between [0.1, 4] for β. For the sake of the integrity of figure plotting, Morlet wavelet admissibility condition (ω0/β≥5) is not considered. However, it should be noted that the admissibi- lity condition is not satisfied at the area pointed by the text arrow in Fig. 3. x = 2exp 2exp 2exp ⎛ ⎜ ⎝ ⎛ ⎜ ⎝ ⎛ ⎜ ⎝ t − 0.0018 − 0.0001 − t 0.0019 − 0.000 09 ⎞ ⎟ ⎠ ⎞ ⎟ ⎠ t sin(2 70 000( π − 0.0018)) + sin(2 90 000( π t − 0.0019)) + − t 0.002 0 − 0.000 08 ⎞ ⎟ ⎠ t sin(2 80 000( π − 0.002 0)) (14) For the convenience of illustration in the next, these three components are denoted as 1, 2, and 3 in time sequence. The sam- pling frequency is 500 kHz. The wave shape in time domain and its frequency analysis are shown in Fig. 4. Fig. 4 Simulated AE signal and its frequency analysis Then the genetic algorithm stated above is used to optimize the two parameters of Morlet wavelet, and Fig. 5 is the curve of best fitness for each generation. It can be seen that when the optimization is processed to the 15th generation, the best result has come out, it’s ω0=2.653, β=0.481. Fig. 5 Optimization result: curve of best fitness Using these parameters, the scalogram of simulation signal[7] is given out, as shown in Fig. 6. On the time-frequency scalogram, three components are easily to differentiate. Comparing these three components, it’s clear that the lower frequency component has higher frequency resolution and lower time resolution; While the higher frequency component has higher time resolution and lower frequency resolution, which is an ideal time-frequency per- formance and manifests the characteristics of wavelet analysis. Meanwhile, another two groups of parameters, ω0=2.653, β=0.2 and ω0=5, β=0.481, are used, and the results are shown in Fig. 7 and Fig. 8. Fig. 6 and Fig. 7 share the same ω0, And it can be seen that: As β decreases, the frequency resolution increases, while the time resolution decreases, and component 2 is mixed with component 1 and 3; Fig. 6 and Fig. 8 share the same β. And Fig. 3 Wavelet entropy on ω0-β plane It can be seen that at the 2D plane, there exists a minimum on the wavelet entropy curve. The wavelet entropy of every point can be calculated one by one, and then the point with minimum entropy can be searched out. Whereas, if the search step is too small, the computation will become unbearable; If the step is too large, the computation precision will be lost. For such search task, genetic algorithm (GA) is much suitable due to its perfect charac- teristics. Thus, in this paper, GA is used to optimize the parameterω0 and β. 2.2.2 Genetic algorithm GA was first introduced by HOLLAND in 1975[9]. As a search process, GA mimics the laws of natural selection and ge- netics, and utilizes group searching strategy and information ex- change among individuals. GA has the characteristics of parallel process, random search, self-adaptive, global optimization, and thus has found widely application in combination optimization, machine learning, adaptive control, etc. GA has been one of the key techniques of intelligent computation in 21st century. A standard GA process mainly includes code, original popu- lation production, fitness calculation, selection, crossover and mutation. In this paper, the population size is selected as 30; The coding method is binary coding. The length of each chromosome is 20, i.e. 10 for ω0 and 10 for β. Fitness function is wavelet en- tropy, and the selection method is roulette wheels. Crossover rate and mutation rate are 0.5, 0.001, respectively. The computation stops when evolved to the 100th generation. In order to satisfy the admissibility condition ω0/β≥5, in the code step, for each given ω0 , β is under the upper limit of ω0/5. 3 SIMULATION Ref. [10] introduced a simulation model of AE signal g m ⎧ ⎪ = ⎨ ⎪ ⎩ x n I = ∑ i 1 = v g − i n k i n=1, 2, 3, … , N (12) 0 <1 > m M m exp t m ∆⎛ − ⎜ τ ⎝ ⎞ ⎟ ⎠ sin(2 f m t π ∆ 0 ) 1 ≤ m M ≤ (13) There are N discrete data points x1, x2,…, xN in the signal, which is comprised of I impulses. Each impulse has M effective points. Based on the given model, a simple AE signal was simu- lated by 3 exponential decaying components 

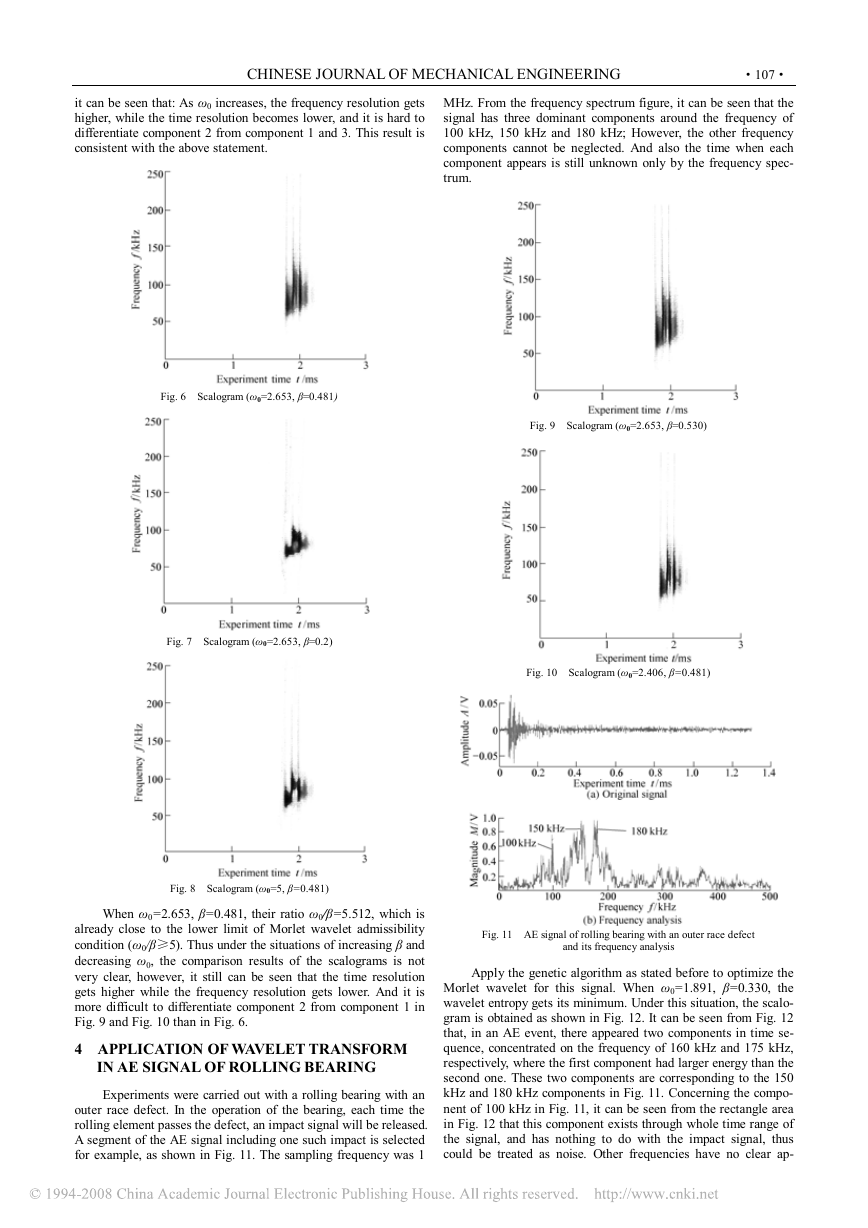
CHINESE JOURNAL OF MECHANICAL ENGINEERING ·107· it can be seen that: As ω0 increases, the frequency resolution gets higher, while the time resolution becomes lower, and it is hard to differentiate component 2 from component 1 and 3. This result is consistent with the above statement. MHz. From the frequency spectrum figure, it can be seen that the signal has three dominant components around the frequency of 100 kHz, 150 kHz and 180 kHz; However, the other frequency components cannot be neglected. And also the time when each component appears is still unknown only by the frequency spec- trum. Fig. 9 Scalogram (ω0=2.653, β=0.530) Fig. 10 Scalogram (ω0=2.406, β=0.481) Fig. 6 Scalogram (ω0=2.653, β=0.481) Fig. 7 Scalogram (ω0=2.653, β=0.2) Fig. 8 Scalogram (ω0=5, β=0.481) When ω0=2.653, β=0.481, their ratio ω0/β=5.512, which is already close to the lower limit of Morlet wavelet admissibility condition (ω0/β≥5). Thus under the situations of increasing β and decreasing ω0, the comparison results of the scalograms is not very clear, however, it still can be seen that the time resolution gets higher while the frequency resolution gets lower. And it is more difficult to differentiate component 2 from component 1 in Fig. 9 and Fig. 10 than in Fig. 6. 4 APPLICATION OF WAVELET TRANSFORM IN AE SIGNAL OF ROLLING BEARING Experiments were carried out with a rolling bearing with an outer race defect. In the operation of the bearing, each time the rolling element passes the defect, an impact signal will be released. A segment of the AE signal including one such impact is selected for example, as shown in Fig. 11. The sampling frequency was 1 Fig. 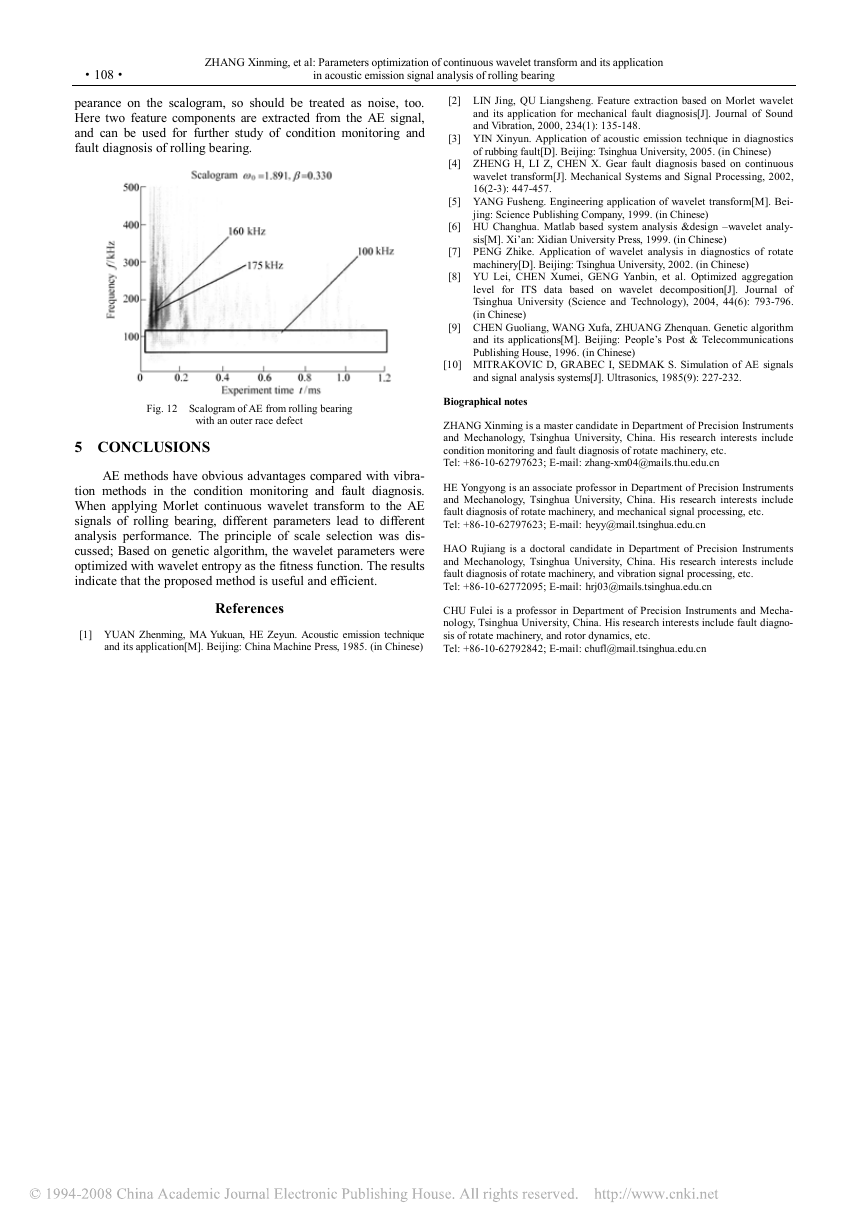11 AE signal of rolling bearing with an outer race defect and its frequency analysis Apply the genetic algorithm as stated before to optimize the Morlet wavelet for this signal. When ω0=1.891, β=0.330, the wavelet entropy gets its minimum. Under this situation, the scalo- gram is obtained as shown in Fig. 12. It can be seen from Fig. 12 that, in an AE event, there appeared two components in time se- quence, concentrated on the frequency of 160 kHz and 175 kHz, respectively, where the first component had larger energy than the second one. These two components are corresponding to the 150 kHz and 180 kHz components in Fig. 11. Concerning the compo- nent of 100 kHz in Fig. 11, it can be seen from the rectangle area in Fig. 12 that this component exists through whole time range of the signal, and has nothing to do with the impact signal, thus could be treated as noise. Other frequencies have no clear ap- 

·108· ZHANG Xinming, et al: Parameters optimization of continuous wavelet transform and its application YZHANG Xinming, et al: Parameters optimization of continuous wavelet transform and its application in acoustic Y in acoustic emission signal analysis of rolling bearing pearance on the scalogram, so should be treated as noise, too. Here two feature components are extracted from the AE signal, and can be used for further study of condition monitoring and fault diagnosis of rolling bearing. Biographical notes Fig. 12 Scalogram of AE from rolling bearing with an outer race defect 5 CONCLUSIONS AE methods have obvious advantages compared with vibra- tion methods in the condition monitoring and fault diagnosis. When applying Morlet continuous wavelet transform to the AE signals of rolling bearing, different parameters lead to different analysis performance. The principle of scale selection was dis- cussed; Based on genetic algorithm, the wavelet parameters were optimized with wavelet entropy as the fitness function. The results indicate that the proposed method is useful and efficient. References [1] YUAN Zhenming, MA Yukuan, HE Zeyun. Acoustic emission technique and its application[M]. Beijing: China Machine Press, 1985. (in Chinese) [2] LIN Jing, QU Liangsheng. Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis[J]. Journal of Sound and Vibration, 2000, 234(1): 135-148. of rubbing fault[D]. Beijing: Tsinghua University, 2005. (in Chinese) [3] YIN Xinyun. Application of acoustic emission technique in diagnostics [4] ZHENG H, LI Z, CHEN X. Gear fault diagnosis based on continuous wavelet transform[J]. Mechanical Systems and Signal Processing, 2002, 16(2-3): 447-457. [5] YANG Fusheng. Engineering application of wavelet transform[M]. Bei- jing: Science Publishing Company, 1999. (in Chinese) [6] HU Changhua. Matlab based system analysis &design –wavelet analy- sis[M]. Xi’an: Xidian University Press, 1999. (in Chinese) [7] PENG Zhike. Application of wavelet analysis in diagnostics of rotate machinery[D]. Beijing: Tsinghua University, 2002. (in Chinese) [8] YU Lei, CHEN Xumei, GENG Yanbin, et al. Optimized aggregation level for ITS data based on wavelet decomposition[J]. Journal of Tsinghua University (Science and Technology), 2004, 44(6): 793-796. (in Chinese) [9] CHEN Guoliang, WANG Xufa, ZHUANG Zhenquan. Genetic algorithm and its applications[M]. Beijing: People’s Post & Telecommunications Publishing House, 1996. (in Chinese) [10] MITRAKOVIC D, GRABEC I, SEDMAK S. Simulation of AE signals and signal analysis systems[J]. Ultrasonics, 1985(9): 227-232. ZHANG Xinming is a master candidate in Department of Precision Instruments and Mechanology, Tsinghua University, China. His research interests include condition monitoring and fault diagnosis of rotate machinery, etc. Tel: +86-10-62797623; E-mail: zhang-xm04@mails.thu.edu.cn HE Yongyong is an associate professor in Department of Precision Instruments and Mechanology, Tsinghua University, China. His research interests include fault diagnosis of rotate machinery, and mechanical signal processing, etc. Tel: +86-10-62797623; E-mail: heyy@mail.tsinghua.edu.cn HAO Rujiang is a doctoral candidate in Department of Precision Instruments and Mechanology, Tsinghua University, China. His research interests include fault diagnosis of rotate machinery, and vibration signal processing, etc. Tel: +86-10-62772095; E-mail: hrj03@mails.tsinghua.edu.cn CHU Fulei is a professor in Department of Precision Instruments and Mecha- nology, Tsinghua University, China. His research interests include fault diagno- sis of rotate machinery, and rotor dynamics, etc. Tel: +86-10-62792842; E-mail: chufl@mail.tsinghua.edu.cn