《工业控制计算机》2008 年 21 卷第 6 期 55 小波去噪方法分析与 Matlab 仿真 王新楼 （兰州交通大学电子与信息工程学院，甘肃 兰州 730070） 小波分析理论是一种新兴的信号处理理论，它在时间上和频率上都有很好的局部性，这使得小波分析非常适合于时- 频分析，借助时- 频局部分析特性，小波分析理论已经成为信号去噪中的一种重要的工具。简述了几种小波去噪方法，其中 的阈值去噪的方法是一种实现简单、效果较好的小波去噪方法。 摘 要 关键词：小波分析，去噪，阈值 Abs tract Wavelet analys is theory is a new theory of s ignal proces s and it has good localization in both frequency and time do- mains .It makes the wavelet analys is s uitable for time - frequency analys is .Wavelet analys is has played a particularly impor- tant role in denois ing,due to the fact that it has the property of time - frequency analys is .In this paper,the method of Wavelet Analys is is analyzed.and the method of thres hold denois ing is a good method of eas y realization and effective to reduce the nois e. Keywords :wavelet analys is ,denois ing,thres hold 由小波变换是一种信号的时频分析，它具有多分辨率的特 点，可以方便地从混有强噪声的信号中提取原始信号，被誉为分 析信号的显微镜。运用小波分析进行信号噪声去除是小波分析的 一个非常重要的应用之一。本文介绍小波消噪的基本原理及其几 种小波去噪方法，并利用 Matlab 软件在计算机上实现了几种方 法下信号的噪声消除，从混有噪声的实际信号中提取了原始信 号，具有非常实用的意义。对处理后的结果进行分析和比较。 1 小波消噪的基本原理 一个含噪声的一维信号的模型可表示为： s （i）=f（i）+σ·e （i） （i=0，1，2，…，n- 1） 式中，f（i）为真实信号；e （i）为噪声；s （i）为含噪信号。这里以 一个简单的噪声模型加以说明，即 e （i）为高斯白噪声 N（0，1）， 噪声级为 1。在实际工程中，有用信号通常表现为低频信号或较 平稳的信号，噪声信号则表现为高频信号，所以去噪过程可按以 下方法进行处理。首先对实际信号进行小波分解，选择小波并确 定分解层次为 N，则噪声部分通常包含在高频中。然后对小波分 解的高频系数进行门限阈值量化处理。最后根据小波分解的第 N 层低频系数和经过量化后的 1～N 层高频系数进行小波重构， 达到消除噪声的目的，即抑制信号的噪声，在实际信号中恢复真 实信号。总体上，对于一维离散信号来说，其高频部分所影响的 是小波分解的第一层细节，其低频部分所影响的是小波分解的 最深层和低频层。 2 小波去噪的方法 2.1 小波分解与重构法去噪 设一个噪声污染的信号模型描述为： S（x）=（f（x）+n1（x））* n2（x） 式中，s （x）表示为降质信号，f（x）表示为原信号，n1（x）表示 加性噪声，n2（x）表示乘性噪声。大多数情况下，信号降质过程可 看成是线性不变模型，上式可改写为： S（x）=f（x）+n（x） 式中，n（x）为高斯白噪声，小波的多分辨分析特性能将信号 在不同尺度下进行多分辨率的分解，并将交织在一起的各种不 同频率组成的混合信号分解成不同频段的子信号，因而对信号 具有按频带处理的能力。因为噪声 n（x）是一个实的、方差为 σ2 的平稳的高斯白噪声，其小波系数的平均功率与尺度成反比。并 且它的离散细节信号的幅值随着小波变换级数的增长而不断减 少。对于所有的尺度，白噪声小波变换的离散细节信号系数的反 差随着尺度的增加会有规律地减少。又因为小波变换是线性变 换，所以降质信号的小波系数是信号的小波系数和噪声的小波 系数的和；降质信号的离散逼近部分和离散细节部分分别是信 号变换后的离散逼近部分和离散细节部分与噪声变换后的离散 逼近部分和离散细节部分的和。因此在消噪过程中，利用信号与 白噪声在小波变换后，它们各自的小波系数的性质不同，可以消 除或减弱噪声。小波分析运用在信号去噪处理，主要表现在以下 方面：是针对信号经小波变换后在不同分辨率下呈现不同规律， 在不同分辨率下设定不同阈值门限，调整小波系数，达到去除噪 声的目的。 利用小波分解与重构去噪的步骤： 1）首先对含噪声信号 f（x）进行小波分解，得到小波变换之 后的逼近部分 c j，k 和细节部分 d j，k； 2）然后取出第 j 层的细节部分 d j，k，根据选定的阈值 δj，用下 列的公式进行处理 d jk = jk 当 d d # 0 当 d jk >δj jk ≤δj 3）最后利用逼近部分 c j，k 和细节部分 d j，k 利用重构算法进 行重构，得到滤波后的信号。 2.2 小波变换阈值去噪 由于小波变换的小波基都是紧支集，因此小波变换具有一 种“集中”的能力，可以使信号的能量在小波变换域集中于少数 系数上，那么相对来说，对这些系数的取值必然大于在小波系数 域内能量分散于大量小波系数的噪声的小波系数值，这个意味 着对小波系数进行阀值处理可以在小波变换域中去除低于固定 幅度的噪声。小波阀值去噪方法可以分为硬阀值法和软阀值法 两种。 其中硬阀值的处理步骤如下： 1）先把信号做小波变换，得到小波系数； 2）计算出阀值，把小波系数的绝对值与阀值进行比较，小于 或等于阀值的点设为零，大于阀值的点保持不变； 

56 小波去噪方法分析与 Matlab 仿真 3）再把处理过的小波系数进行小波变换来重构信号。 软阀值的处理步骤如下： 1）含噪信号进行小波分解，选择合适的小波，确定小波的分 解 层 次 M， 并 对 信 号 进 行 二 进 离 散 小 波 分 解 。 可 选 用 Daubichie 4 小波，可通过正确设计的 QFM( 正交镜像滤波器) 来实现。 2）对信号分解后的各级系数进行适当处理：对第 1 到第 M 层的小波系数，选择一个软阈值，对每一级的小波系数进行阈值 量化处理。 3）信号的重构：对量化处理后的各级小波系数进行信号的 小波重构。 Matlab 中获取阈值的函数有：ddencmp 、ths elect、wbm- pen、wdcbm。Matlab 中实现信号阈值去噪的函数有：wden、 wdencmp 、wthres h、wthcoef、wpthcoef、wpdencmp 。 3 Matlab 中信号去噪实例实现与分析 下面对信号 leleccum 进行实例分析，信号长度（即采样点 数）N=1024，含噪信号是由于原始信号 leleccum 叠加白噪声组 成的。通过 matlab 进行去噪仿真。下面分别是基于小波分解与 重构法去噪（图 1）、硬阈值去噪（图 2）、软阈值去噪（图 3）的仿 真图。 图 1 小波分解与重构法去噪 图 2 硬阈值去噪 从三种去噪的防真结果可以看出：利用小波分解与重构法 去噪，会将高频系数强制置 0 后通过重构信号，会损失信号的部 分细节，若为图象去噪会使其变得模糊，而小波阈值去噪的方法 相比小波分解与重构法而言效果较好。但硬阈值去噪。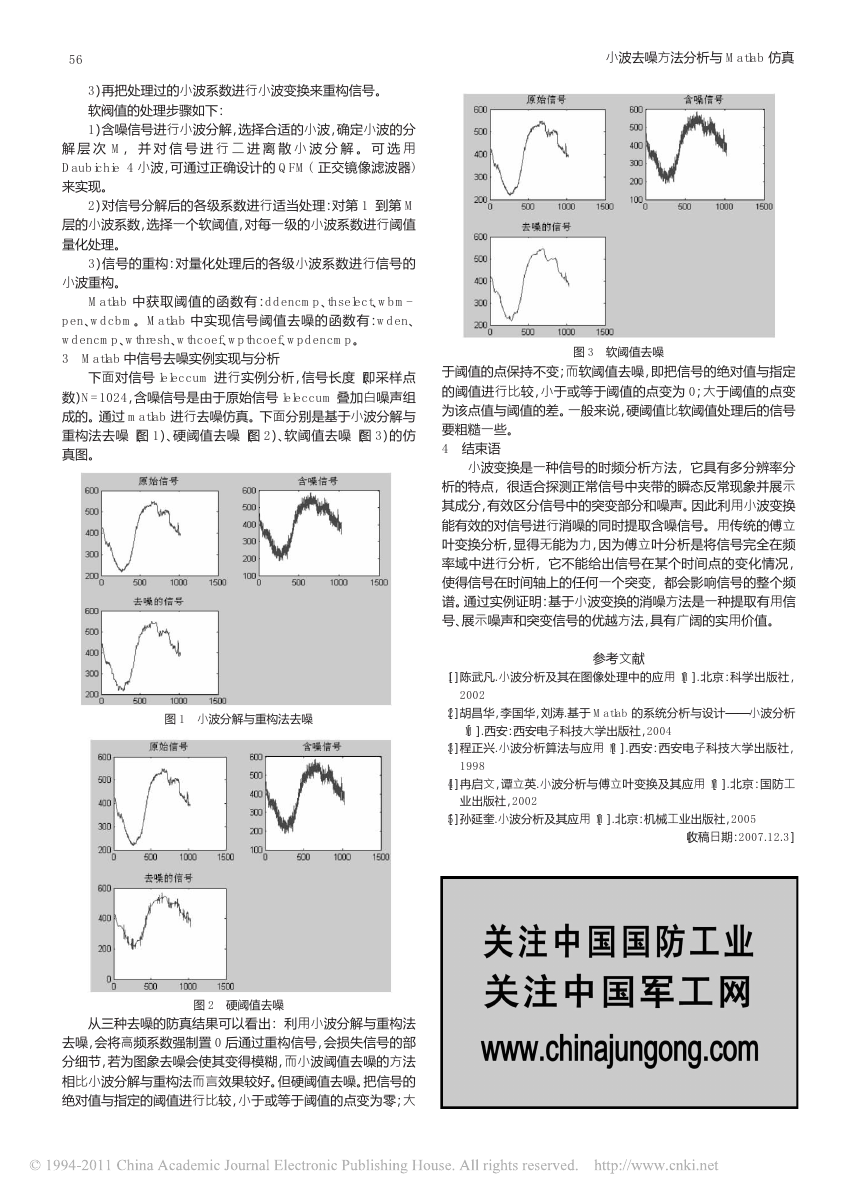把信号的 绝对值与指定的阈值进行比较，小于或等于阈值的点变为零；大 图 3 软阈值去噪 于阈值的点保持不变；而软阈值去噪，即把信号的绝对值与指定 的阈值进行比较，小于或等于阈值的点变为 0；大于阈值的点变 为该点值与阈值的差。一般来说，硬阈值比软阈值处理后的信号 要粗糙一些。 4 结束语 小波变换是一种信号的时频分析方法，它具有多分辨率分 析的特点，很适合探测正常信号中夹带的瞬态反常现象并展示 其成分，有效区分信号中的突变部分和噪声。因此利用小波变换 能有效的对信号进行消噪的同时提取含噪信号。用传统的傅立 叶变换分析，显得无能为力，因为傅立叶分析是将信号完全在频 率域中进行分析，它不能给出信号在某个时间点的变化情况， 使得信号在时间轴上的任何一个突变，都会影响信号的整个频 谱。通过实例证明：基于小波变换的消噪方法是一种提取有用信 号、展示噪声和突变信号的优越方法，具有广阔的实用价值。 ［1］陈武凡.小波分析及其在图像处理中的应用［M］.北京：科学出版社， 参考文献 2002 ［2］胡昌华，李国华，刘涛.基于 Matlab 的系统分析与设计———小波分析 ［M］.西安：西安电子科技大学出版社，2004 ［3］程正兴.小波分析算法与应用［M］.西安：西安电子科技大学出版社， 1998 ［4］冉启文，谭立英.小波分析与傅立叶变换及其应用［M］.北京：国防工 业出版社，2002 ［5］孙延奎.小波分析及其应用［M］.北京：机械工业出版社，2005 ［收稿日期：2007.12.3］