logo资料库

1stOpt使用教程（特别适合自学）.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：1.27M 资料格式：pdf 举报 版权申诉
第1页 / 共38页
第2页 / 共38页
第3页 / 共38页
第4页 / 共38页
第5页 / 共38页
第6页 / 共38页
第7页 / 共38页
第8页 / 共38页
资料共38页，剩余部分请下载后查看
    A
    七维高科有限公司 综合优化软件包1stOpt使用手册 第一篇 1stOpt 简介 1．1: 概要 1stOpt 是七维高科有限公司（7D-Soft High Technology Inc.）独立开发， 拥有完全自主知识产权的一套数学优化分析综合工具软件包。在非线性回归，曲 线拟合，非线性复杂模型参数估算求解，线性/非线性规划等领域傲视群雄，首屈 一指，居世界领先地位。除去简单易用的界面，其计算核心是基于七维高科有限 公司科研人员十数年的革命性研究成果【通用全局优化算法】(Universal Global Optimization - UGO)，该算法之最大特点是克服了当今世界上在优化计算领域中 使用迭代法必须给出合适初始值的难题，即用户勿需给出参数初始值，而由 1stOpt 随机给出，通过其独特的全局优化算法，最终找出最优解。以非线性回归为例， 目前世界上在该领域最有名的软件工具包诸如 Matlab, OriginPro, SAS, SPSS, DataFit, GraphPad 等，均需用户提供适当的参数初始值以便计算能够收敛并找到 最优解。如果设定的参数初始值不当则计算难以收敛，其结果是无法求得正确结 果。而在实际应用当中，对大多数用户来说，给出(猜出)恰当的初始值是件相当 困难的事，特别是在参数量较多的情况下，更无异于是场噩梦。而 1stOpt 凭借其 超强的寻优，容错能力，在大多数情况下（大于 90%)，从任一随机初始值开始， 都能求得正确结果。 1．2: 国内外类似软件概况 数据综合分析领域，国外软件无疑占绝对统治地位。在非线性曲线拟合，参数优化方面， 名声大，应用广的有诸如OriginPro，Matlab，SAS，SPSS，DataFit，GraphPad，TableCurve2D， TableCurve3D 等 。 无 论 这 些 软 件 界 面 ， 历 史 ， 名 声 如 何 ， 最 常 用 算 法 有 麦 夸 特 法 （Levenberg-Marquardt）或简面体爬山法（Simplex Method）等，均可归属于局部最优法。 因而如何有效地确定参数初始值始终是难以克服的瓶颈，由于此，一些实际问题可能永远无 法获得正解。国内方面，因无自己独特有效的技术理论与方法，虽有个别分析软件面市，与 上述国外类似产品相比，功能相差甚远，即使在国内也无竞争优势，在国际上就更无声影了。 而 1stOpt凭借自己革命性的算法理论，在非线性拟合，参数估算等优化领域强于目前世界上 任何已知软件包，其英文版已远销美国，德国，法国，英国，芬兰，瑞典，荷兰，南非，澳 大利亚，新西兰，土耳其等国。 1
    七维高科有限公司 1．3： 1stOpt 应用的优化算法 最优化算法包括： 1) Levenberg-Marquardt 法 (LM) + 通 用 全 局 优 化 算 法 (Universal Global Optimization - UGO) 2) Quasi-Newton 法 (BFGS) + 通用全局优化算法(Universal Global Optimization - UGO) 3) 遗传算法 (Genetic Algorithms - GA) 4) 摸拟退火 (Simulated Annealing - SA) 5) 下山単体法 (Simplex Method - SM) + 通用全局优化算法(Universal Global Optimization - UGO) 6) 离子群法 (Particle Swarm Optimization - PSO) 7) 最大继承法 (Max Inherit Optimization - MIO) 8) 差分进化法 (Differential Evolution - DE) 9) 自组织群移法 (Self-Organizing Migrating Algorithms - SOMA) 10) 共 扼 梯 度 法 (Conjugate-Gradient Method - CGM) + 通 用 全 局 优 化 算 法 (Universal Global Optimization - UGO) 11) 包维尔法 (Powell Optimization - PO) + 通用全局优化算法(Universal Global Optimization - UGO) 12) 禁忌搜索法 (Tabu Search - TS) 13) 单纯线性规划法 (Simplex Linear Program) 1．4： 1stOpt 应用范围 1) 模型自动优化率定 2) 参数估算 3) 任意模型公式线性，非线性拟合，回归 4) 非线性连立方程组求解 5) 任意维函数，隐函数极值求解 6) 隐函数根求解，作图，求极值 7) 线性，非线性及整数规划 8) 组合优化问题 9) 高级计算器 1．5： 1stOpt 特长 1) 功能强劲，是目前唯一能以任何初始值而求得美国国家标准与技术研究院 (NIST：National Institute of Standards and Technology)非线性回归测试 题集最优解的软件包。 2) 可广泛用于水文水资源及其它工程模型优化计算。内镶 VB 及 Pascal 语言，可 帮助描述处理复杂模型。 3) 可连接由任何语言（C++, Fortran, Basic, Pascal…）编译而成的外部目标函 数动态连接库或命令行可执行文件。 4) 非线性曲线拟合可处理任意类型模型公式，任意多数目的待求参数及变量 5) 模型自动率定时可同时处理多个数据文件 6) 可非常容易处理一些特殊的参数，如降雨径流模型中的流域初期土壤含水量 7) 可同时处理多个输出量 8) 实时显示计算结果 9) 可直接读存 Excel，CSV 等格式文件 2
    七维高科有限公司 10) 界面简单友好，使用方便 11) 自带有上百个实例，覆盖范围包括几乎所有优化方面。通过不同类型实例，用 户可轻松掌握 1stOpt 的用法。 1．6: 1stOpt 关键词 表.1：主要关键词 关键词名 定义参数 意义及示例 例： 定义 a, b, c, d 四个参数： Parameter a, b, c, d； 例： 定义 a1, a2, a3, a4, a5, a6, a7, a8, a9, a10 十个参数： Parameter a1, a2, a3, a4, a5, a6, a7, a8, a9, a10； Parameter 也可简写为： Parameter a(1:10); 例： 定义参数 a，其取值范围在【-1，1】，初始值为 0.5 Parameter a = 0.5 [-1, 1]; 例： 定义参数 a 为整数，其取值范围在【-100，100】 Variable Parameter a[-100,100,0]; 定义变量 例：定义 x, y, z 三个变量： Variable x, y, z; 定义函数 Function 例：两变量曲线拟合： Function y = a + b*exp(c – x); 例：两变量函数优化： Function (x+((2-x)*(2+y))^2)*sin(x*y); 定义常量 Constant 例：两变量曲线拟合： Function y = a + b*exp(c – x); 例：两变量函数优化： Function (x+((2-x)*(2+y))^2)*sin(x*y); 定义常字符串量 例：两变量曲线拟合： Function y = a*（c-x）^2 + b*exp((c – x)^4); ConstStr 可写为： ConstStr B ＝ （c-x）^2 Function y = a*B + b*exp(B^2); VarConstant 定义变常量，详情见 2.4 节 VarParameter 定义变参数，详情见 2.4 节 Data 定义数据开始 DataFile 定义数据文件 NewDivision 定义新得代码块 StartProgram 编程模式开始 EndProgram 编程模式结束 Maximum Minimum 求最大值 求最小值 PlotFunction 画函数图 Algorithms 定义优化方法 3
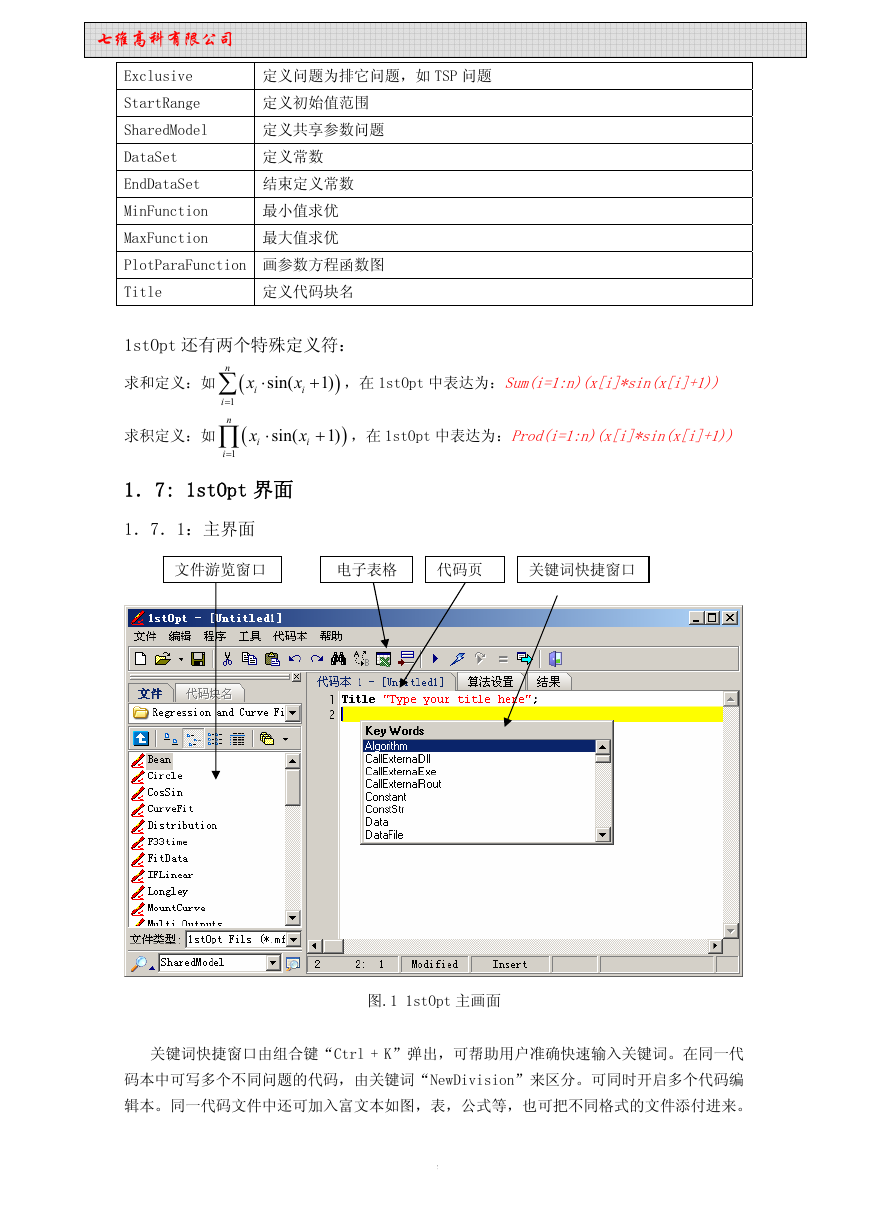
    七维高科有限公司 Exclusive 定义问题为排它问题，如 TSP 问题 StartRange 定义初始值范围 SharedModel 定义共享参数问题 DataSet 定义常数 EndDataSet 结束定义常数 MinFunction 最小值求优 MaxFunction 最大值求优 PlotParaFunction 画参数方程函数图 Title 定义代码块名 1stOpt 还有两个特殊定义符： ∑ 求和定义：如 ( sin( 1) x i ) x i + ⋅ n i 1 = n i 1 = ，在 1stOpt 中表达为：Sum(i=1:n)(x[i]*sin(x[i]+1)) ∏ 求积定义：如 ( x i ⋅ sin( x i + 1) ) ，在 1stOpt 中表达为：Prod(i=1:n)(x[i]*sin(x[i]+1)) 1．7: 1stOpt 界面 1．7．1：主界面 文件游览窗口 电子表格 代码页 关键词快捷窗口 图.1 1stOpt 主画面 关键词快捷窗口由组合键“Ctrl + K”弹出，可帮助用户准确快速输入关键词。在同一代 码本中可写多个不同问题的代码，由关键词“NewDivision”来区分。可同时开启多个代码编 辑本。同一代码文件中还可加入富文本如图，表，公式等，也可把不同格式的文件添付进来。 4
    七维高科有限公司 1．7．2：数据处理电子表格 1stFit 电子表格类似与 Excel，多表单，支持公式，直接输入输出到 Excel，文本文件 （.txt，.csv），树型表单管理，直观并可分类，可方便用于数据前，后处理。 图.2 1stOpt 电子表格 1．7．3：输入代码 每一句代码以‘；’号作结束符。如 Parameter a, b, c, d; Constant p1 = 1, p2 = 4, p3 = 5; 对曲线拟合，对二维，缺省自变量名为 x，因变量名为 y；对三维或多维，缺省自变量名 为 x1，x2, x3…,因变量名为 y。如下两段代码效果等同，右边代码中无需再定义变量和参数， 将由 1stOpt 自动识别。 代码 1 Variables x, y; Parameters a, b, c, d; Function y=a-b*exp(-c*x^d); Data; 0.05 0.15 0.25 0.35 0.13 0.13 0.19 0.34 代码 2 Function y=a-b*exp(-c*x^d); Data; 0.05 0.15 0.25 0.35 0.13 0.13 0.19 0.34 对函数优化，如参数没有范围限制，也可省去参数定义，下列左右两段代码效果等同 代码 1 Parameters x, y; Minimum = True; Function exp(sin(50*x)) +sin(60*exp(y)) + sin(70*sin(x))+sin(sin(80*y))- sin(10*(x+y)) +(x^2+y^2)/4; 代码 2 MinFunction exp(sin(50*x)) +sin(60*exp(y)) sin(70*sin(x))+sin(sin(80*y))- sin(10*(x+y)) +(x^2+y^2)/4; 5
    七维高科有限公司 1．7．4：执行计算 因为 1stOpt 的初始值通常是随机产生，一次计算不成功，并非意味下次亦同样不成功， 反之亦然。按快捷键”F9”执行计算，“F10“中止计算。 1．7．5：优化算法设定 在 1stOpt 中，共有 13 种有化算法。不同的问题该选用何种算法？一般而言： 非线性回归，曲线拟合问题： 1) Levenberg-Marquardt 法 (LM) + 通 用 全 局 优 化 算 法 (Universal Global Optimization - UGO) 2) BFGS + 通用全局优化算法(Universal Global Optimization - UGO) 3) 下山単体法 (Simplex Method - SM) + 通用全局优化算法(Universal Global Optimization - UGO) 4) 差分进化法 5) 最大继承法 函数优化，方程求根问题： 1) 下山単体法 (Simplex Method - SM) + 通用全局优化算法(Universal Global Optimization - UGO) 2) BFGS + 通用全局优化算法(Universal Global Optimization - UGO) 3) 差分进化法 4) 最大继承法 线性规划问题： 1) 单纯线性规划法 (Simplex Linear Program - SLP) 2) 下山単体法 (Standard Simplex Method - SM) + 通用全局优化算法(Universal Global Optimization - UGO) 3) 差分进化法 优化组合问题： 1) 最大继承法 2) 禁忌搜索法 3) 模拟退火 4) 遗传算法 6
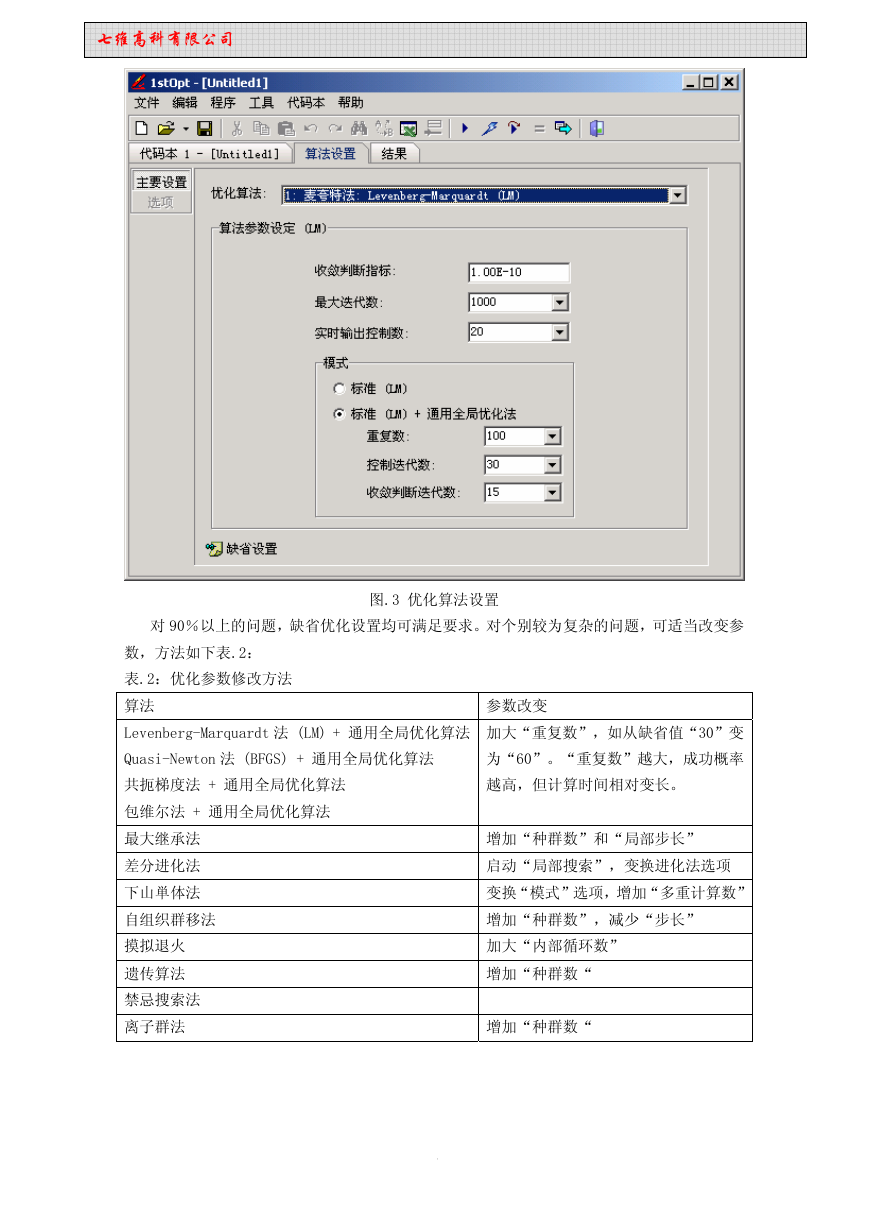
    七维高科有限公司 对 90％以上的问题，缺省优化设置均可满足要求。对个别较为复杂的问题，可适当改变参 图.3 优化算法设置 数，方法如下表.2： 表.2：优化参数修改方法 算法 参数改变 Levenberg-Marquardt 法 (LM) + 通用全局优化算法 加大“重复数”，如从缺省值“30”变 Quasi-Newton 法 (BFGS) + 通用全局优化算法 为“60”。“重复数”越大，成功概率 共扼梯度法 + 通用全局优化算法 越高，但计算时间相对变长。 包维尔法 + 通用全局优化算法 最大继承法 差分进化法 下山単体法 自组织群移法 摸拟退火 遗传算法 禁忌搜索法 离子群法 增加“种群数”和“局部步长” 启动“局部搜索”，变换进化法选项 变换“模式”选项，增加“多重计算数” 增加“种群数”，减少“步长” 加大“内部循环数” 增加“种群数“ 增加“种群数“ 7
    七维高科有限公司 第二篇 1stOpt 应用 2．1：求任意形式，任意维数，约束或非约束的函数最优值。 1stOpt 即可用于无约束函数求优，也可用于有约束函数求优。约束函数即可是不等式也可 是等式。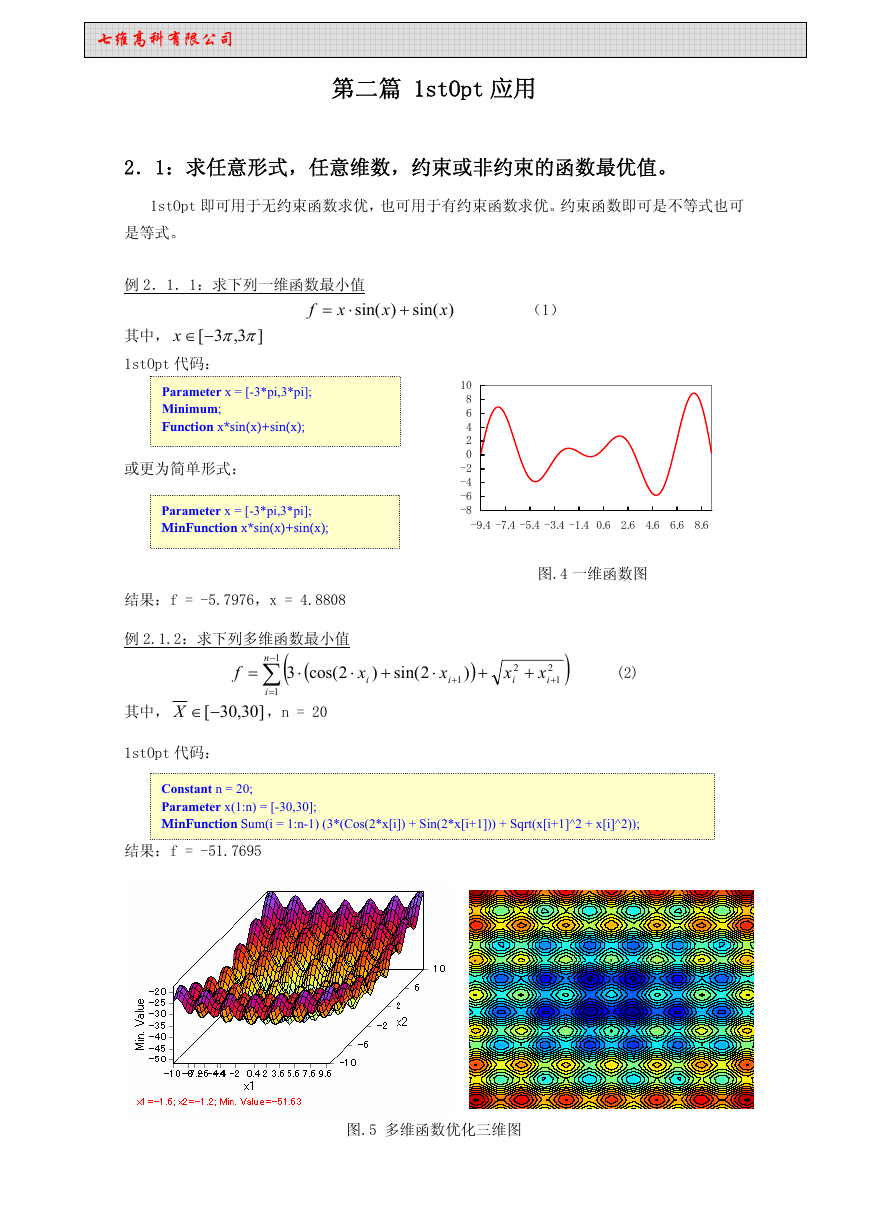 例 2．1．1：求下列一维函数最小值 sin( x ⋅= f x ) + sin( x ) （1） 10 8 6 4 2 0 -2 -4 -6 -8 -9.4 -7.4 -5.4 -3.4 -1.4 0.6 2.6 4.6 6.6 8.6 图.4 一维函数图 x i ) + sin( 2 ⋅ x 1) + i ) + x 2 i + x 2 i 1 + ) (2) 其中， ππ−∈x ]3,3[ 1stOpt 代码： Parameter x = [-3*pi,3*pi]; Minimum; Function x*sin(x)+sin(x); 或更为简单形式： Parameter x = [-3*pi,3*pi]; MinFunction x*sin(x)+sin(x); 结果：f = -5.7976，x = 4.8808 例 2.1.2：求下列多维函数最小值 n 1 ( 3 ( cos( 2 ⋅ ⋅ f = ∑− ]30,30 i 1 = ，n = 20 [−∈X 其中， 1stOpt 代码： Constant n = 20; Parameter x(1:n) = [-30,30]; MinFunction Sum(i = 1:n-1) (3*(Cos(2*x[i]) + Sin(2*x[i+1])) + Sqrt(x[i+1]^2 + x[i]^2)); 结果：f = -51.7695 图.5 多维函数优化三维图 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料