logo资料库

华南农业大学机器视觉试卷.pdf

发布时间：2022-06-05 发布人：admin 分类：说明书 资料大小：0.41M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    华南农业大学期末考查试题 200920092009～2010 2009 201020102010 学年第 2222 学期 考试科目：《机器视觉》 2010.12.15 2010.12.15 提交时间：2010.12.15 2010.12.15 考试类型：开放考查作业 学号： 姓 名： 年级专业 一 二 三 四 五 六 七 总分 题号 得分 评阅人 ………………………………………………………………………………………………………… 一、填空题（每题2222 分，共16161616 分） 1. 图像数字化包括 采样 和 量化 两过程。 2. 图像处理中常用的两种邻域是 3×3 和 5×5 。 3. 从图像工程的角度上，机器视觉过程一般分为四个阶段，包括数字化成像、图像处理、图 像分析和 模型匹配 等。图像分割 技术是由图像处理向图像分析阶段过渡过程中必须的。 4. 机器视觉系统通常由光源、 光学成像系统 、 图像捕捉系统 、 图像采集与数字化、 智 能图像处理与决策模块 和控制执行机构等部分组成。 5. 一般来说，采样间距越大，图像数据量 越少 ，质量 越低 ；反之亦然。 6. 结构元素S在区域X内移动时其原点位置的集合就是S对X的 腐蚀 。 7. 图像分割方法可以分成基于边缘的分割和基于 区域 的分割两类，前者是利用不同目标 间像素属的 不连续性 实现目标分割的。 8. 常见的一阶微分边缘检测算子有 正交梯度算子 、 平滑梯度算子 和Roberts 等算子。 二、选择题（每题1 分，共9 分） 1.一幅灰度级均匀分布的图像，其灰度范围在[0，255] ，则该图像像素的存储位数为 d 。 a. 2 b.4 c.6 d.8 2.图像与灰度直方图间的对应关系是： b 。 a.一一对应 b. 多对一 c. 一对多 d. 多对多 3.下列关于区域形状的特征描述中，不正确是： b 。 a.矩形度是物体面积与其最小外接矩形面积之比 b.边界的形状数具有平移、旋转和比例缩放不变性 c.当区域为圆时，圆形度达到最大值1
    d.归一化的中心矩具有平移、旋转、比例缩放不变性 4.计算机显示器的颜色模型为: c 。 a. CMYK b. HIS c. RGB d. YIQ 5. 大小为1024X1024 ，灰度级别为256 色的图像文件大小为： b . a. 512KB b. 1MB c. 1.5MB d. 2MB 6. 下列图像边缘检测算子中抗噪性能最好的是： b . a. 梯度算子 b. Prewitt 算子 c. Roberts 算子 d. Laplacian 算子 7. 下列图像平滑算法中既能有效地平滑噪声又可以避免边缘模糊效应的是： b . a. 领域平均法 b. 中值滤波法 c. 低通滤波法 d. 灰度变换法 8. 关于数学形态学处理, 以下说法正确的是: d . a. 先膨胀后腐蚀的运算称为开运算。 b. 先腐蚀后膨胀的运算称为闭运算。 c. 细化是将一个曲线型物体细化为一条单像素宽的线，以图形化显示出其拓扑性质。 d. 消除连续区域内的小噪声点，可以通过连续多次使用开闭运算 9. 能够检测45°斜线的的模版是： b -1 -1 -1 2 2 -1 -1 -1 2 a. b. -1 -1 2 -1 2 -1 -1 -1 2 -1 -1 -1 2 2 2 -1 -1 -1 c. -1 -1 2 -1 2 -1 2 -1 -1 d. 三、判断改错题（下列说法是否正确，正确的就在题号前的括弧内打√， 错 误的打×并改正。每题1 分，共5 分） ( √ ) 1. 灰度直方图能反映一幅图像各灰度级像元占图像的面积比。 ( √ ) 2. 共点直线群的Hough 变换是一条正弦曲线。 ( √ ) 3. 边缘检测是将边缘像素标识出来的一种图像分割技术。 ( √ ) 4. Laplacian 算子是一种局部运算，图像的二值化则是一种点运算。 ( × ) 5. 腐蚀运算满足交换律和结合律。“腐蚀”改为“膨胀”
    四、简答题（每题4 分，共20 分） 1. 简述直方图均衡化的原理和特点 答：直方图均衡化是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全 部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸，重新分配图像像 素值，使一定灰度范围内的像素数量大致相同。直方图均衡化就是把给定图像的直方图 分布改变成“均匀”分布直方图分布。 特点:增加像素灰度值的动态范围，提高图像对比度。 2. 简述区域生长算法的一般步骤。 答：区域算法步骤： 1.确定分割的区域数目，并在每个区域选择或确定一个能正确代表该区域灰度取值的像 素点（种子点）； 2.选择有意义特征和领域方式； 3.确定相似性准则。 3. 简要说明开运算和闭运算分别在图像处理与分析中的作用。 答：1.先腐蚀后膨胀称为开运算：开运算能够有效地消除细小物体、毛刺，能在纤细 连接点处分离物体，能平滑较大物体的边界但不明显改变物体的形状、面积和位置。 2.先膨胀后腐蚀称为闭运算：闭运算能够有效地填充物体内部细小的空洞，连接临近 物体，能在不明显改变物体面积的情况下平滑物体的边界。 4. 简述图像平滑、图像锐化和边缘检测模板各自的特点 答：图像平滑的特点：模板内系数全为正，且之和为1；对常数图像处理前后不变， 对一般图像处理前后平均亮度不变。 图像锐化特点：模板内系数有正有负，且之和为1；对常数图像处理前后不变，对一 般图像处理前后平均亮度不变。 边缘检测模板的特点：模板内系数有正有负，且之和为0；对常数图像处理后为0， 对一般图像处理后为边缘点。
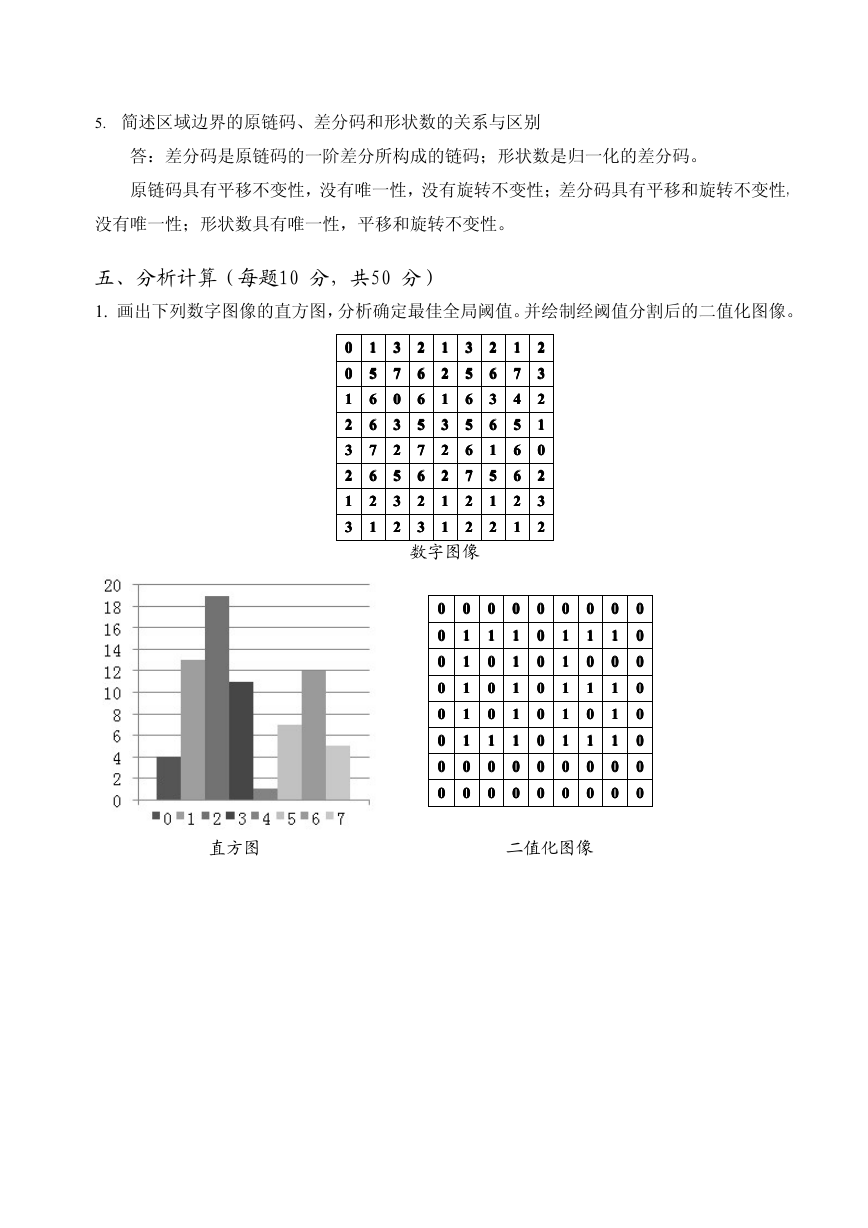
    5. 简述区域边界的原链码、差分码和形状数的关系与区别 答：差分码是原链码的一阶差分所构成的链码；形状数是归一化的差分码。 原链码具有平移不变性，没有唯一性，没有旋转不变性；差分码具有平移和旋转不变性， 没有唯一性；形状数具有唯一性，平移和旋转不变性。 五、分析计算（每题10 分，共50 分） 1. 画出下列数字图像的直方图，分析确定最佳全局阈值。并绘制经阈值分割后的二值化图像。 0000 0000 1111 2222 3333 2222 1111 3333 1111 5555 6666 6666 7777 6666 2222 1111 3333 7777 0000 3333 2222 5555 3333 2222 1111 2222 1111 3333 2222 2222 1111 1111 3333 2222 5555 6666 6666 6666 5555 5555 6666 7777 7777 6666 2222 2222 3333 2222 数字图像 0000 0000 0000 0000 0000 0000 0000 0000 0000 1111 1111 1111 1111 1111 0000 0000 2222 6666 3333 6666 1111 5555 1111 2222 0000 1111 0000 0000 0000 1111 0000 0000 1111 7777 4444 5555 6666 6666 2222 1111 0000 1111 1111 1111 1111 1111 0000 0000 2222 3333 2222 1111 0000 2222 3333 2222 0000 0000 0000 0000 0000 0000 0000 0000 0000 1111 1111 1111 1111 1111 0000 0000 0000 1111 0000 1111 0000 1111 0000 0000 0000 1111 0000 1111 1111 1111 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 直方图 二值化图像
    2. 绘制X 被结构元素S 腐蚀后的图像。 3. 给定结构元素S为一个3×3 正方形，如何采用数学形态学方法提取图中所示月球的轮廓 （边界）？ 写出算法流程。如果结构元素换成5×5 的正方形，提取到的边界会有何变化？ 答：算法流程： 第一，图像分割（二值化）； 第二，用结构元素S对图像进行腐蚀； 第三，把二值化的图像减去腐蚀后的图像。 这样就可以得出图像的内边界。如果结构元素换成 5×5 的正方形，那么提取到的边界会加粗。 4. 给出图像中黑色区域的边界描述：写出各自的原链码、差分码和形状数（※号表示起点像 素）。 图像A 图像B
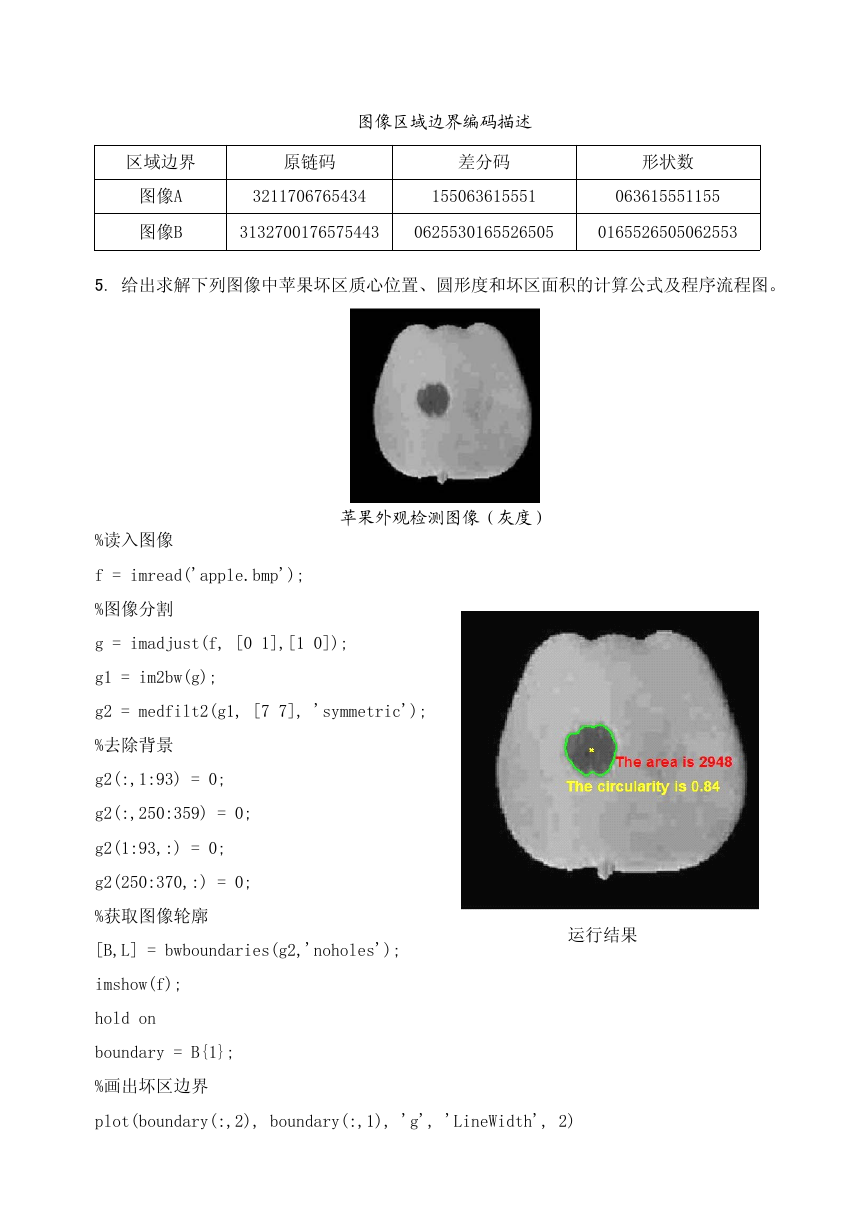
    图像区域边界编码描述 区域边界 原链码 差分码 形状数 图像A 图像B 3211706765434 155063615551 063615551155 3132700176575443 0625530165526505 0165526505062553 5. 给出求解下列图像中苹果坏区质心位置、圆形度和坏区面积的计算公式及程序流程图。 苹果外观检测图像（灰度） %读入图像 f = imread('apple.bmp'); %图像分割 g = imadjust(f, [0 1],[1 0]); g1 = im2bw(g); g2 = medfilt2(g1, [7 7], 'symmetric'); %去除背景 g2(:,1:93) = 0; g2(:,250:359) = 0; g2(1:93,:) = 0; g2(250:370,:) = 0; %获取图像轮廓 [B,L] = bwboundaries(g2,'noholes'); 运行结果 imshow(f); hold on boundary = B{1}; %画出坏区边界 plot(boundary(:,2), boundary(:,1), 'g', 'LineWidth', 2)
    % 计算坏区的周长 delta_sq = diff(boundary).^2; perimeter = sum(sqrt(sum(delta_sq,2))); % 获得区域面积 stats = regionprops(L,'Area','Centroid'); area = stats(1).Area; % 计算圆形度 metric = 4*pi*area/perimeter^2; % 显示圆形度 metric_string = sprintf('The circularity is %2.2f',metric); text(boundary(1,2),boundary(80,1)+50,metric_string,'Color','y',... 'FontSize',14,'FontWeight','bold'); %计算并显示坏区面积 area_string = sprintf('The area is %d',area); text(boundary(90,2),boundary(100,1),area_string,'Color','r',... 'FontSize',14,'FontWeight','bold'); %找出质心 x = boundary(:,2); y = boundary(:,1); abc=[x y ones(length(x),1)]\[-(x.^2+y.^2)]; a = abc(1); b = abc(2); c = abc(3); xc = -a/2; yc = -b/2; %显示质心 plot(xc,yc,'yx','LineWidth',2);
    分享到：
    赞 收藏

    相关推荐

    资料库

    考试认证

    共收录20637份资料，累计11个分类，关注成员有19位，主要包括：真题,美赛,软考,PMP,Linux/Unix认证,思科认证,微软认证,Oracle认证,华为认证,软考等考,其它

    热门标签

    真题 美赛 软考 PMP Linux/Unix认证 思科认证 微软认证 Oracle认证 华为认证 软考等考 其它

    最新资料