logo资料库

matlab瑞利衰落仿真.doc

发布时间：2022-06-01 发布人：admin 分类：说明书 资料大小：0.27M 资料格式：doc 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
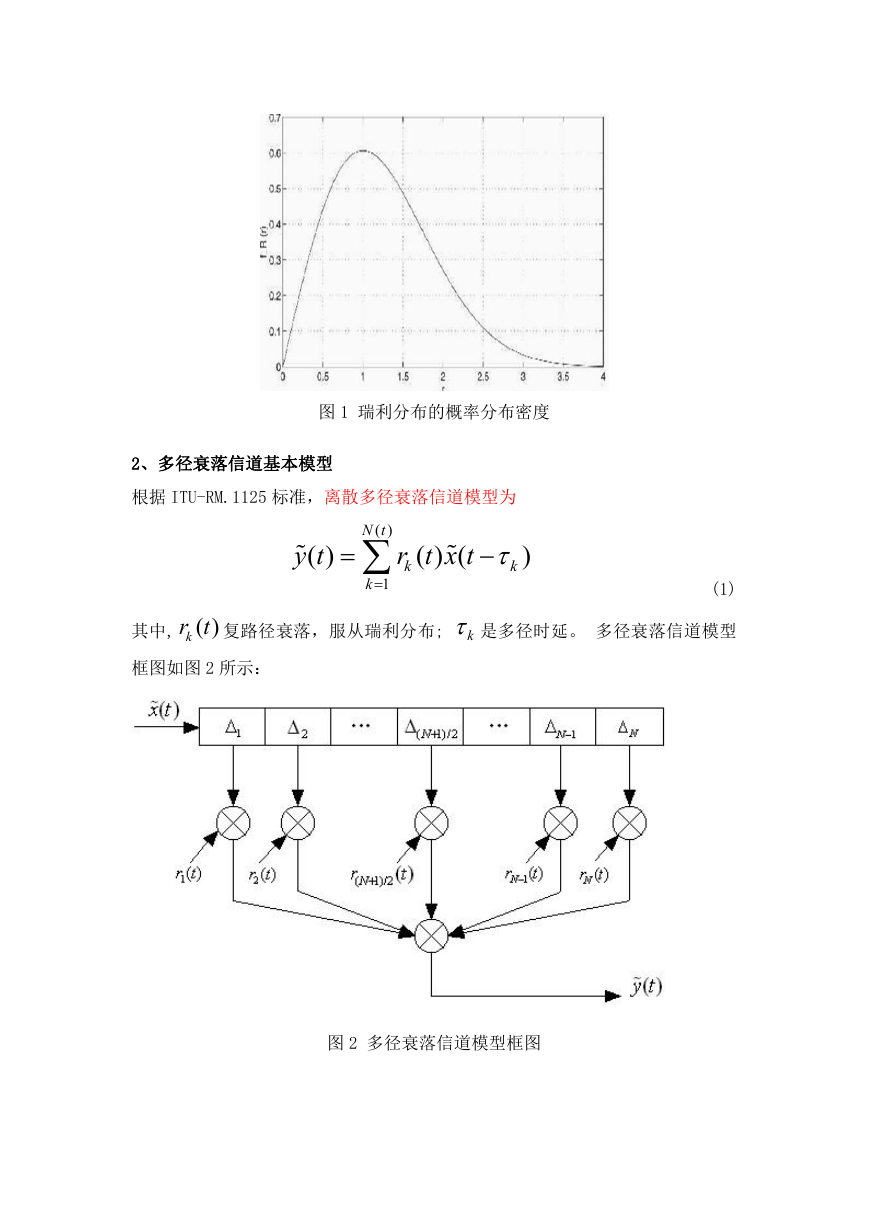
    引言 由于多径和移动台运动等影响因素，使得移动信道对传输信号在时间、频率 和角度上造成了色散，如时间色散、频率色散、角度色散等等，因此多径信道的 特性对通信质量有着至关重要的影响，而多径信道的包络统计特性成为我们研究 的焦点。根据不同无线环境，接收信号包络一般服从几种典型分布，如瑞利分布、 莱斯分布和 Nakagami-m 分布。在本文中，专门针对服从瑞利分布的多径信道进 行模拟仿真，进一步加深对多径信道特性的了解。 仿真原理 1、瑞利分布简介 环境条件： 通常在离基站较远、反射物较多的地区，发射机和接收机之间没有直射波路 径，存在大量反射波；到达接收天线的方向角随机且在（0~2π）均匀分布；各 反射波的幅度和相位都统计独立。 幅度、相位的分布特性： 包络 r 服从瑞利分布，θ在 0～2π内服从均匀分布。瑞利分布的概率分布 密度如图 1 所示：
    图 1 瑞利分布的概率分布密度 2、多径衰落信道基本模型 根据 ITU-RM.1125 标准，离散多径衰落信道模型为 ( ) y t   ( ) N t  k 1  r t x t  k k ( ) (   ) (1) 其中, ( ) kr t 复路径衰落，服从瑞利分布; k 是多径时延。 多径衰落信道模型 框图如图 2 所示： 图 2 多径衰落信道模型框图
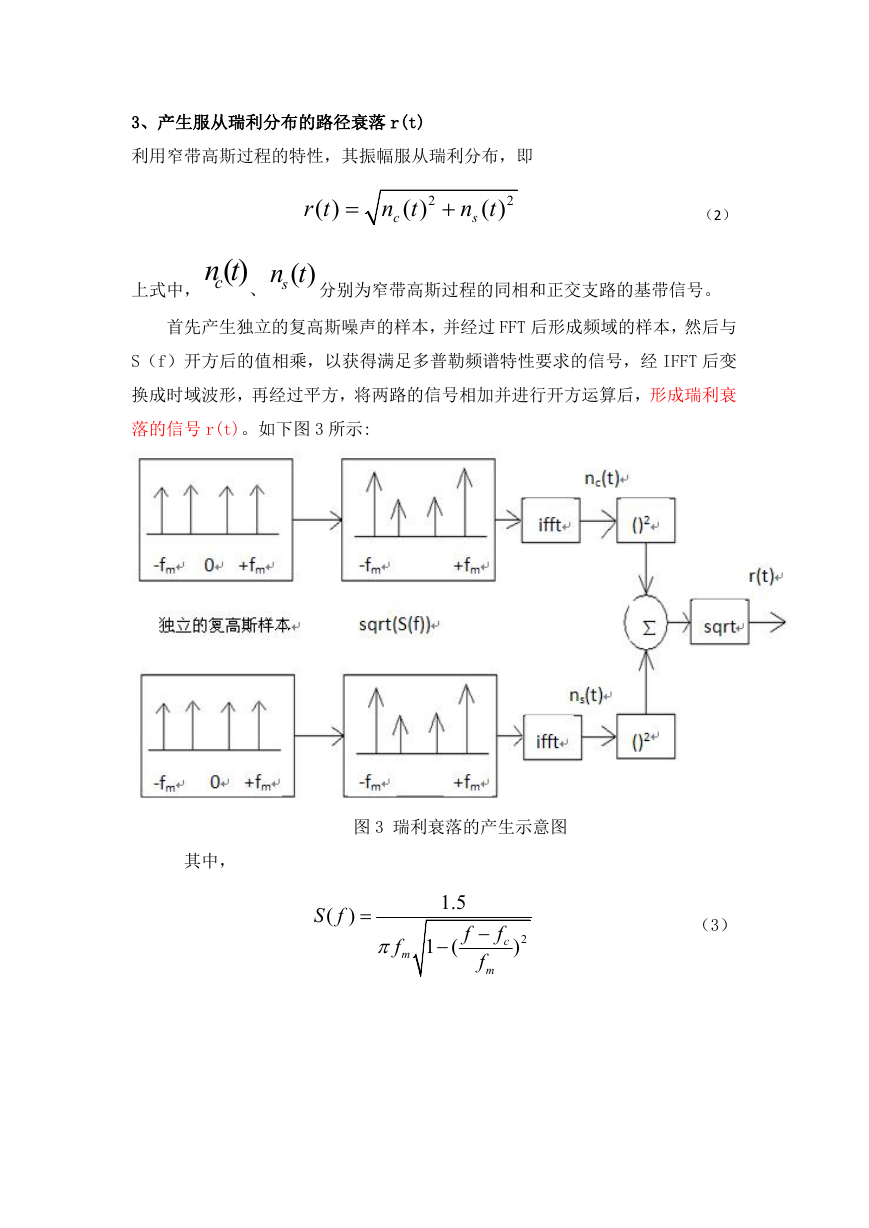
    3、产生服从瑞利分布的路径衰落 r(t) 利用窄带高斯过程的特性，其振幅服从瑞利分布，即 ( ) r t  2 ( ) n t c  2 ( ) n t s （2） 上式中， ( )cn t 、 ( ) sn t 分别为窄带高斯过程的同相和正交支路的基带信号。 首先产生独立的复高斯噪声的样本，并经过 FFT 后形成频域的样本，然后与 S（f）开方后的值相乘，以获得满足多普勒频谱特性要求的信号，经 IFFT 后变 换成时域波形，再经过平方，将两路的信号相加并进行开方运算后，形成瑞利衰 落的信号 r(t)。如下图 3 所示: 图 3 瑞利衰落的产生示意图 其中， ( S f )  1.5 f 1 (   f m f  f m 2 )c （3）
    4、 产生多径延时 k 多径/延时参数如表 1 所示： 表 1 多径延时参数 Tap Relative delay (ns) Average power (dB) 1 2 3 4 5 6 0 310 710 1 090 1 730 2 510 0 -1.0 -9.0 -10.0 -15.0 -20.0 仿真框架 根据多径衰落信道模型（见图 2），利用瑞利分布的路径衰落 r(t)（见图 3） 和多径延时参数 k （见表 1），我们可以得到多径信道的仿真框图，如图 4 所示；
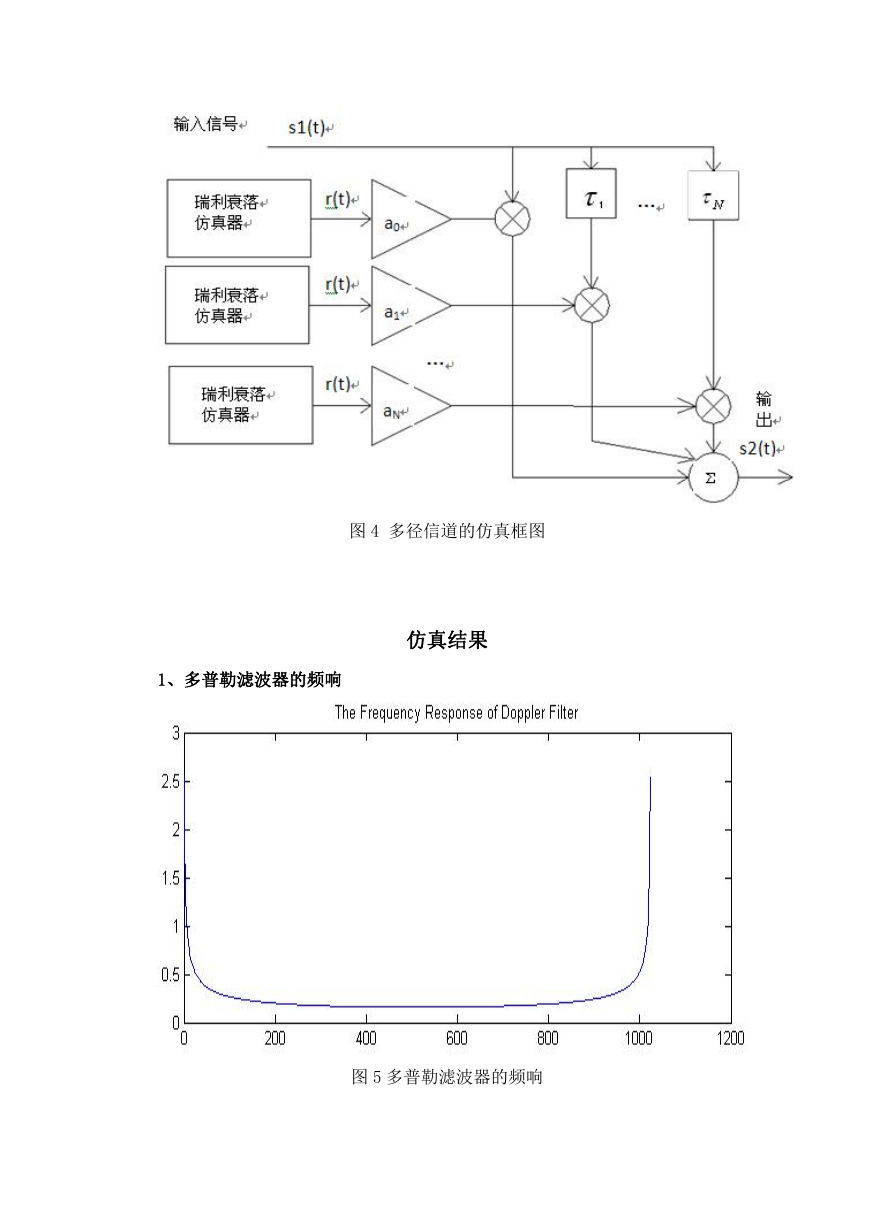
    图 4 多径信道的仿真框图 1、多普勒滤波器的频响 仿真结果 图 5 多普勒滤波器的频响
    2、多普勒滤波器的统计特性 图 6 多普勒滤波器的统计特性 3、信道的时域输入/输出波形
    图 7 信道的时域输入/输出波形 小组分工 程序编写：吴溢升 报告撰写：谭世恒 仿真代码
    %main.m clc; LengthOfSignal=10240; %信号长度(最好大于两倍fc) fm=512; %最大多普勒频移 fc=5120; %载波频率 t=1:LengthOfSignal; % SignalInput=sin(t/100); SignalInput=sin(t/100)+cos(t/65); %信号输入 delay=[0 31 71 109 173 251]; power=[0 -1 -9 -10 -15 -20]; %dB y_in=[zeros(1,delay(6)) SignalInput]; %为时移补零 y_out=zeros(1,LengthOfSignal); %用于信号输出 for i=1:6 Rayl; y_out=y_out+r.*y_in(delay(6)+1-delay(i):delay(6)+LengthOfSignal-delay(i))*10^(power (i)/20); end; figure(1); subplot(2,1,1); plot(SignalInput(delay(6)+1:LengthOfSignal)); %去除时延造成的空白信号 title('Signal Input'); subplot(2,1,2); plot(y_out(delay(6)+1:LengthOfSignal)); %去除时延造成的空白信号 title('Signal Output'); figure(2); subplot(2,1,1); hist(r,256); title('Amplitude Distribution Of Rayleigh Signal') subplot(2,1,2); hist(angle(r0)); title('Angle Distribution Of Rayleigh Signal'); figure(3); plot(Sf1); title('The Frequency Response of Doppler Filter');
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料