基于小波变换的音频信号去噪 向瑾 翟成瑞 杨 卫 孟令军 张文栋 (电子测试技术国家重点实验室 山西 太原 030051 ) ( 中北大学 电子科学技术系 山西 太原 030051) 摘要：本文主要介绍基于小波变换的软阈值和硬阈值在数据处理中的应用，并用 Matlab 软 件进行仿真。 关键词：小波变换；去噪；软阈值；硬阈值 中图分类号：N37 文献标识码：B Sound signal denoising based on wavelet transform Xiang jin Zhai Chengrui Yang Wei Meng Lingjun Zhang Wendong （National Key Laboratory for Electronic Measurement Technology, Taiyuan 030051, China） Department of electronic science and technology, North University of China, Taiyuan 030051，china Abstract: The paper mainly introduce the soft threshold denoising and the hard threshold denoising based on wavelet transform in processing signal,and simulate the result using Matlab. Keywords: Wavelet transform denoising soft threshold hard threshold 1 引言 数字信号处理技术已经广泛应用在语音、雷达、声纳、地震、图像、控制、生物医学、 遥感遥控、地质勘探、航空航天、故障检测、自动仪表等领域，在信号分析中如何从随机噪 声中有效提取较弱的有用信息，是多学科目前研究的热点内容。对于音频信号进行去噪预处 理成为信号处理的关键所在，所以选取合理的信号去噪方法也变得尤为重要，对于信号去噪 常用的滤波方法有线性滤波、中值滤波、加权递推平均滤波以及几种方法结合的复合滤波， 但是这些平滑滤波方法容易导致信号目标识别能力降低，传统的方法是使用傅立叶变换，但 是傅立叶变换只能体现整个时域到整个频域的变换,信号在时域的瞬息变化在频域不能反映 出来，而在傅立叶分析的基础上发展起来的小波变换，克服了傅立叶变换在这方面的不足。 2 小波变换理论 设ψ（t）∈ 2L (R) ( 2L (R)表示平方可积的实数空间，即能量有限的信号空间），其傅立 叶变换为ψ（ω）。当ψ（ω）满足允许条件： C =Ψ R∫ Ψ ( ) ω ω d ω < ∞ (1) 时，我们称ψ（t）为一个基本小波或母小波（Mother Wavelet）。将母函数ψ（t）经伸缩或 平移后，就可以得到一个小波序列。 对于连续的情况，小波序列为 ψ tba )(, ( = ψ 1 a bt − a ) a,b∈R; a 0≠ (2) 

其中 a 为伸缩因子，b 为平移因子。 对于离散的情况，小波序列为 ψ kj , t )( = j − ψ 2( 2 2 − j t − k ) j,k∈Z (3) 对于任意的函数 f(t) ∈ 2L (R)的连续小波变换为 baW f =<),( f , ψ ba , >= 1 ∫ a R f t )( ( ψ bt − a dt ) （4） 3 小波阈值去噪原理 假设有如下一观测信号: x (t) = s (t) + n (t) (5) 其中 x (t) 为含噪信号, s (t) 为原始信号, n (t) 为高斯白噪声,服从 N (0, 2σ )分布。 对 x (t)作离散小波变换,可得: xω (j,k) = sω (j,k) + nω (j,k), j=0, 1, 2, ... , J, k=0, 1, 2, …, N (6) sω (j,k) 和 nω (j,k)分别是含噪信号,原始信号和噪声在第 j 层上的小波系数;J 为 其中 xω (j,k), 小波变换的最大分解层数;N 为信号的长度。 由于小波变换是线性变换,因此对含噪信号 x (t) 作离散小波变换后,得到的小波系数 xω (j,k),记为 kj,ω ,仍由两部分组成:一部分是原始信号 s (t) 的小波系数 sω (j,k),记为 kj,µ ，另 一部分是噪声 n(t)对应的小波系数 nω (j,k),记为 kj,υ 。 小波阈值去噪方法的基本思想是:当 kj, ^ ω 小于某一阈值时, ^ ω 主要由噪声引起,可认 kj, kj,ν ,可将其舍去;当 ^ ω ≈ ^ ω 。软硬阈值法都是对大于阈值部分的 kj, kj, ^ ω 大于某一阈值时,小波系数主要由信号引起,可认为 kj, 为 kj, kj,µ ≈ ^ ω 进行处理。前者是将该部分小波系数 按一个固定量向零收缩;后者直接取 kj, ^ ω = kj,µ 。然后用处理后的小波系数 kj, ^ ω 进行小波重 构,得到去噪后的信号 )( ^ ts 。 图 1 小波阈值去噪原理 图 2（a）软阈值函数 图 2 （b）硬阈值函数 小波阈值去噪方法的关键步骤是阈值处理,这部分包括阈值的估计和阈值函数的选 

取,Donoho 提出的软、硬阈值函数分别如式（7）, (8)所示: sgn( kj,ω )( kj,ω －λ), kj,ω ≥λ ^ ω = kj, ^ ω = kj, 0 kj,ω <λ kj,ω kj,ω ≥λ 0 kj,ω <λ (7) 其中 sgn(• )为符号函数,阈值λ取 ^ ts 在最小均方误差意义上是有效的。 σ 计信号 )( (8) 。在文献[2]中证明了由此方法得到的估 N ) 2 log( 4．用 MATLAB 软件实现小波去噪 应用 MATLAB 进行仿真，仿真采用实际测到的音频信号数据并采用 Donoho 所使用的 Bumps 信号来作验证信号，输入信噪比为 3，采用 sym8 作为小波基,小波分解的尺度为 5 。 （一） 对所测数据进行去噪 图 1 采集到的数据 图 2 软阈值去噪 图 3 硬阈值去噪 图 4 傅立叶变换去噪 

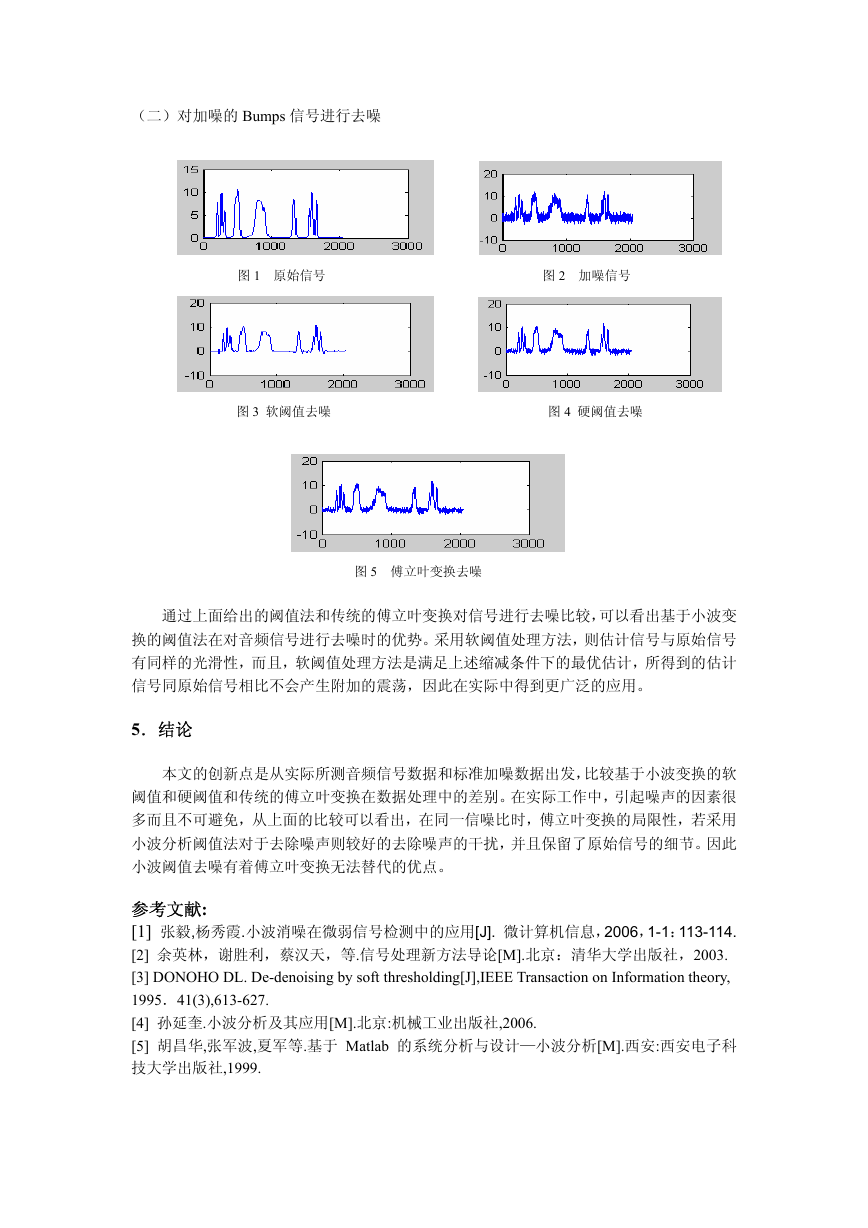
（二）对加噪的 Bumps 信号进行去噪 图 1 原始信号 图 2 加噪信号 图 3 软阈值去噪 图 4 硬阈值去噪 图 5 傅立叶变换去噪 通过上面给出的阈值法和传统的傅立叶变换对信号进行去噪比较，可以看出基于小波变 换的阈值法在对音频信号进行去噪时的优势。采用软阈值处理方法，则估计信号与原始信号 有同样的光滑性，而且，软阈值处理方法是满足上述缩减条件下的最优估计，所得到的估计 信号同原始信号相比不会产生附加的震荡，因此在实际中得到更广泛的应用。 5．结论 本文的创新点是从实际所测音频信号数据和标准加噪数据出发，比较基于小波变换的软 阈值和硬阈值和传统的傅立叶变换在数据处理中的差别。在实际工作中，引起噪声的因素很 多而且不可避免，从上面的比较可以看出，在同一信噪比时，傅立叶变换的局限性，若采用 小波分析阈值法对于去除噪声则较好的去除噪声的干扰，并且保留了原始信号的细节。因此 小波阈值去噪有着傅立叶变换无法替代的优点。 参考文献: [1] 张毅,杨秀霞.小波消噪在微弱信号检测中的应用[J]. 微计算机信息，2006，1-1：113-114. [2] 余英林，谢胜利，蔡汉天，等.信号处理新方法导论[M].北京：清华大学出版社，2003. [3] DONOHO DL. De-denoising by soft thresholding[J],IEEE Transaction on Information theory, 1995．41(3),613-627. [4] 孙延奎.小波分析及其应用[M].北京:机械工业出版社,2006. [5] 胡昌华,张军波,夏军等.基于 Matlab 的系统分析与设计—小波分析[M].西安:西安电子科 技大学出版社,1999. 

作者简介：向瑾（1982-），女（汉族），中北大学硕士研究生；研究方向：信号处理 Xiang Jin(1982-), female(the Han nationality),master graduate student of North University of China, major in signal processing. 联系方式：山西省太原市中北大学 18 系电子测试技术国家重点实验室 205 室 向瑾（收） 邮编：030051 E-mail: xiangjin208@163.com 单位：中北大学电子测试技术国家重点实验室 山西 太原 030051 （National Key Laboratory For Electronic Measurement Technology of North University of China, Taiyuan， 030051, China） 导师简介：翟成瑞(1964-),男（汉族），副教授，主要从事动态测试技术与智能仪器。 Zhai Chengrui（1964-), male(the Han nationality), associate professor , Mainly engaged in the dynamic test technology and the intelligent instrument. 基金资助项目：“十一五”预研项目资助（编号：秘密） 文章编号：200612150947195685