spss中介调节实际操作.doc-资料库

e5b284a6-11bf-451f-a951-29e677a21779.doc.pdf-第1页.png

第1页 / 共18页

e5b284a6-11bf-451f-a951-29e677a21779.doc.pdf-第2页.png

第2页 / 共18页

e5b284a6-11bf-451f-a951-29e677a21779.doc.pdf-第3页.png

第3页 / 共18页

e5b284a6-11bf-451f-a951-29e677a21779.doc.pdf-第4页.png

第4页 / 共18页

e5b284a6-11bf-451f-a951-29e677a21779.doc.pdf-第5页.png

第5页 / 共18页

e5b284a6-11bf-451f-a951-29e677a21779.doc.pdf-第6页.png

第6页 / 共18页

e5b284a6-11bf-451f-a951-29e677a21779.doc.pdf-第7页.png

第7页 / 共18页

e5b284a6-11bf-451f-a951-29e677a21779.doc.pdf-第8页.png

第8页 / 共18页

调节效应重要理论及操作务实一、调节效应回归方程：调节效应是交互效应的一种，是有因果指向的交互效应，而单纯的交互效应可以互为因果关系；调节变量一般不受自变量和因变量影响，但是可以影响自变量和因变量；调节变量一般不能作为中介变量，在特殊情况下，调节变量也可以作为中介变量，例如认知归因方式既可以作为挫折性应激（X）和应对方式（Y）的调节变量也可以作为中介变量。常见的调节变量有性别、年龄、收入水平、文化程度、社会地位等。在统计回归分析中，检验变量的调节效应意味着检验调节变量和自变量的交互效应是否显著。以最简单的回归方程为例，调节效应检验回归方程包括 2 个如下： y=a+bx+cm+e y=a+bx+cm+c’mx+e 1） 2）在上述方程中，m 为调节变量，mx 为调节效应，调节效应是否显著即是分析 C’是否显著达到统计学意义上的临界比率.05 水平)。二、检验调节效应的方法有三种： 1.在层次回归分析中（Hierarchical regression）,检验 2 个回归方程的复相关系数 R1 2 和 R2 2 是否有显著区别，若 R1 2 和 R2 2 显著不同，则说明 mx 交互作用显著，即表明 m 的调节效应显著； 2.或看层次回归方程中的 c’系数（调节变量偏相关系数），若 c’ （spss 输出为标准化ß值）显著，则说明调节效应显著； 3.多元方差分析，看交互作用水平是否显著；

4.在分组回归情况下，调节效应看各组回归方程的 R2。注：上述四种方法主要用于显变量调节效应检验，且和 x 与 m 的变量类型相关，具体要根据下述几种类型采用不同的方式检验三、显变量调节效应分析的几种类型根据调节效应回归方程中自变量和调节变量的几种不同类型组合，分析调节效应的方法和操作也有区别如下： 1.分类自变量（x）+分类调节变量(m) 如果自变量和调节变量都是分类变量的话，实际上就是多元方差分析中的交互作用显著性分析，如 x 有两种水平，m 有三种水平，则可以做 2×3 交互作用方差分析，在 spss 里面可以很容易实现，这我就不多讲了，具体操作看 spss 操作工具书就可以了。 2.分类自变量（x）+连续调节变量（m）这种类型调节效应分析需要对分类自变量进行伪变量转换，将自变量和调节变量中心化（计算变量离均差）然后做层次回归分析。分类自变量转换为伪变量的方法：假设自变量 X 有 n 种分类，则可以转换为 n-1 个伪变量，例如自变量为年收入水平，假设按人均年收入水平分为 8 千以下、8000~2 万、2 万~5 万、5 万~10 万、10 万以上四种类型，则可以转换为 3 个伪变量如下： 10 万以上 5 万到 10 万 2 万到 5 万 8 千以下 x1 1 0 0 0 x2 0 1 0 0 x3 0 0 1 0 上述转换在 spss 中可以建立 3 个伪变量 x1、x2、x3,变量数据中心化后标准回归方程表示为：

y=b1x1+b2x2+b3x3+cm+e y=b1x1+b2x2+b3x3+cm+c1mx1+c2mx2+c3mx3+e 3) 4) x1=1 表示 10 万以上；x2=1 表示 5 万到 10 万；x3=1 表示 2 万到 5 万； 8 千以下=0。此时 8 千以下的回归方程表示为：y=cm +e(在 x1、x2、 x3 上的伪变量值为 0)；之所以单独列出这个方程，是为了方便大家根据回归方程画交互作用图,即求出 c 值就可以根据方程画出 8 千以下变量的调节效应图。检验方法为分析 R2 显著性或调节系数 C’显著性。注：在这 4 种分类自变量的调节效应分析中，采用 R1 2 和 R2 2 显著性检验时，是对 4 种类型自变量在调节变量作用下的调节效应的整体检验，总体显著的效果可能会掩盖某种类型自变量与调节变量的交互作用不显著的情况，此时，我们就要逐一审查各个交互项的偏相关系数。对方程 4）而言，如果检查调节变量的偏相关系数，则有可能会出现一些调节变量偏相关系数不显著的情况，例如，c1 显著、c2 和 c3 不显著或 c1 和 c2 显著，c3 不显著的情况等，此时可根据交互项的偏相关系数来发现到底是那种类型的自变量与调节变量的交互作用不显著。 3.连续自变量（x）+分类调节变量（m）这种类型的调节效应需要采用分组回归分析，所谓分组回归分析既是根据调节变量的分类水平，建立分组回归方程进行分析，回归方程为 y=a+bx+e。当然也可以采用将调节变量转换为伪变量以后进行层次回归分析，层次回归具体步骤同上，见三、2，需要注意的是，分

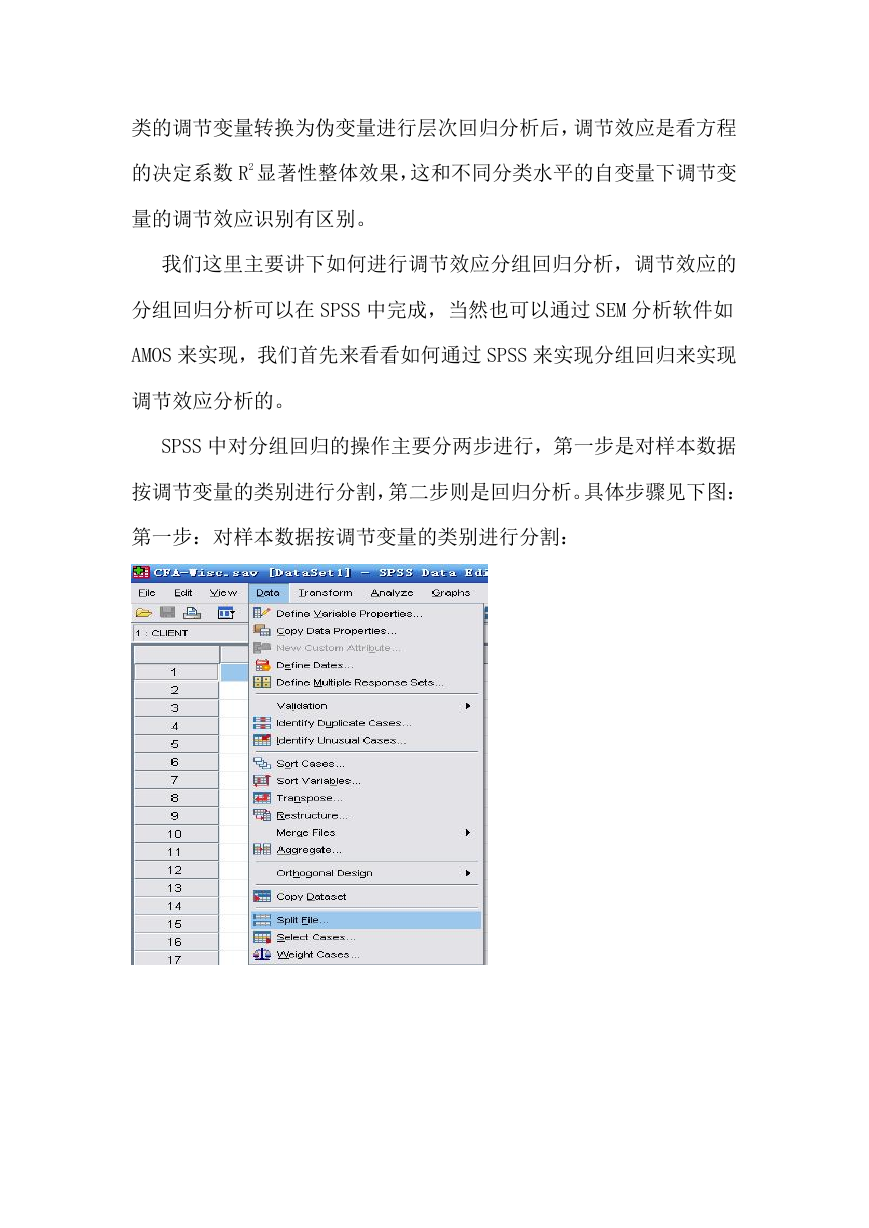
类的调节变量转换为伪变量进行层次回归分析后，调节效应是看方程的决定系数 R2 显著性整体效果，这和不同分类水平的自变量下调节变量的调节效应识别有区别。我们这里主要讲下如何进行调节效应分组回归分析，调节效应的分组回归分析可以在 SPSS 中完成，当然也可以通过 SEM 分析软件如 AMOS 来实现，我们首先来看看如何通过 SPSS 来实现分组回归来实现调节效应分析的。 SPSS 中对分组回归的操作主要分两步进行，第一步是对样本数据按调节变量的类别进行分割，第二步则是回归分析。具体步骤见下图：第一步：对样本数据按调节变量的类别进行分割：

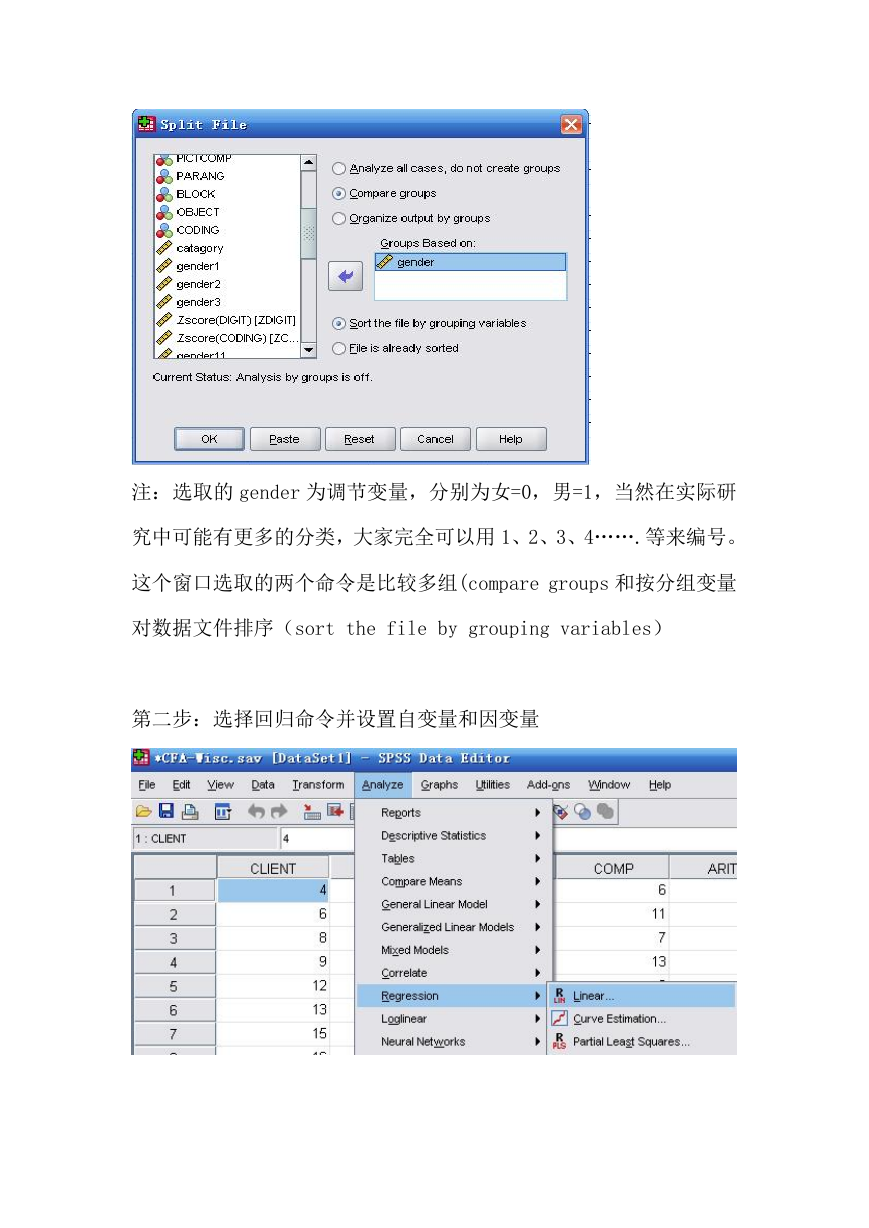
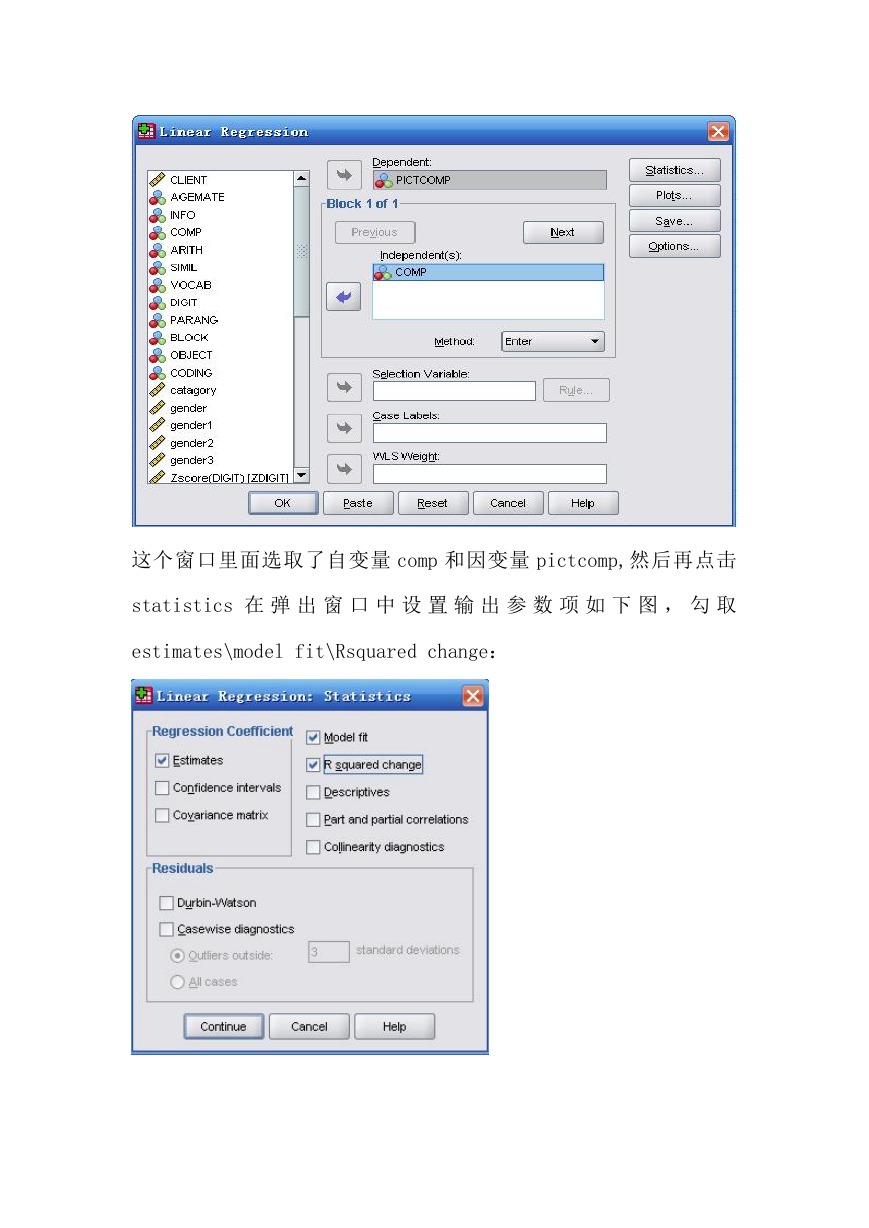
注：选取的 gender 为调节变量，分别为女=0，男=1，当然在实际研究中可能有更多的分类，大家完全可以用 1、2、3、4…….等来编号。这个窗口选取的两个命令是比较多组(compare groups 和按分组变量对数据文件排序（sort the file by grouping variables）第二步：选择回归命令并设置自变量和因变量

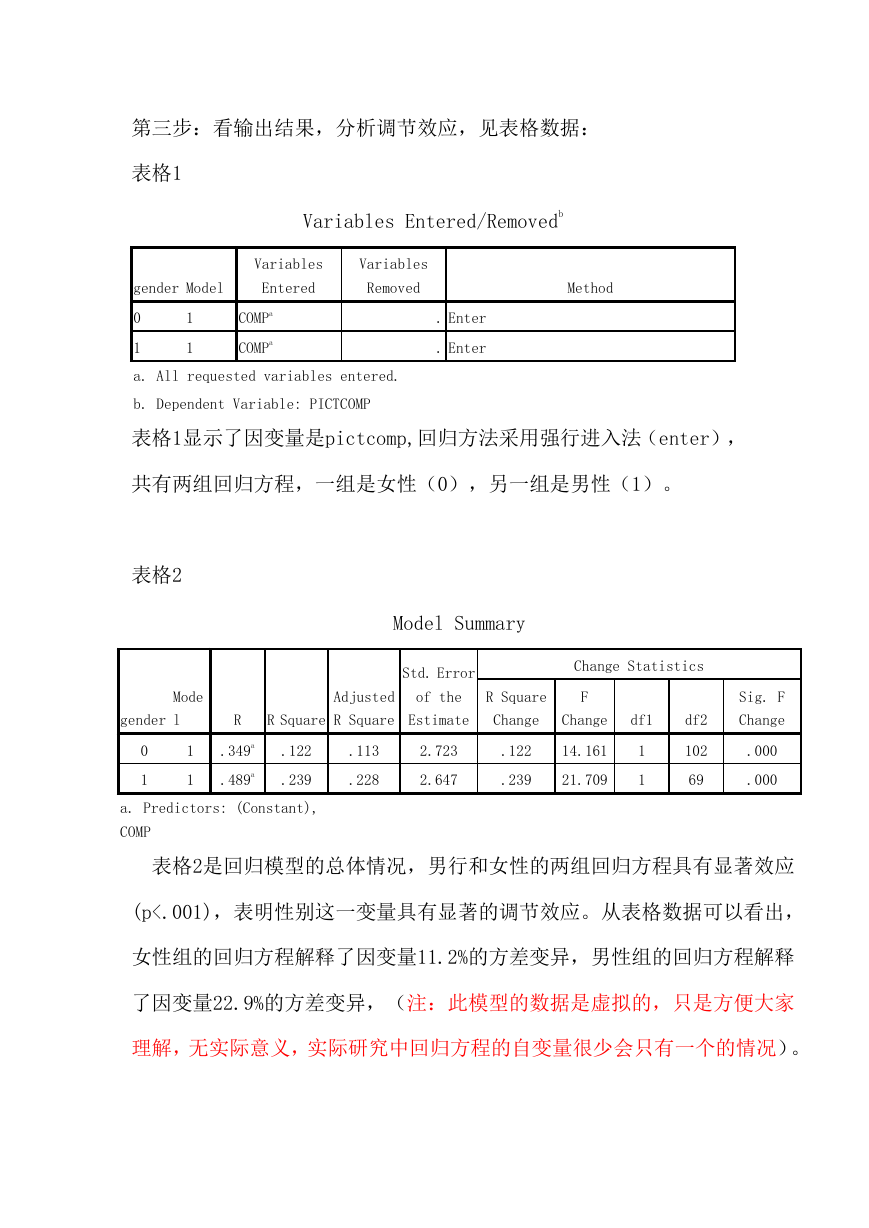
这个窗口里面选取了自变量 comp 和因变量 pictcomp,然后再点击 statistics 在弹出窗口中设置输出参数项如下图，勾取 estimates\model fit\Rsquared change：

第三步：看输出结果，分析调节效应，见表格数据：表格1 Variables Entered/Removedb Variables Variables gender Model Entered Removed Method 0 1 1 1 COMPa COMPa . Enter . Enter a. All requested variables entered. b. Dependent Variable: PICTCOMP 表格1显示了因变量是pictcomp,回归方法采用强行进入法（enter），共有两组回归方程，一组是女性（0），另一组是男性（1）。表格2 Model Summary Std. Error Change Statistics Mode Adjusted of the R Square F gender l R R Square R Square Estimate Change Change df1 0 1 1 1 .349a .489a .122 .239 .113 .228 2.723 2.647 .122 .239 14.161 21.709 1 1 Sig. F Change .000 .000 df2 102 69 a. Predictors: (Constant), COMP 表格2是回归模型的总体情况，男行和女性的两组回归方程具有显著效应 (p<.001)，表明性别这一变量具有显著的调节效应。从表格数据可以看出，女性组的回归方程解释了因变量11.2%的方差变异，男性组的回归方程解释了因变量22.9%的方差变异，（注：此模型的数据是虚拟的，只是方便大家理解，无实际意义，实际研究中回归方程的自变量很少会只有一个的情况）。

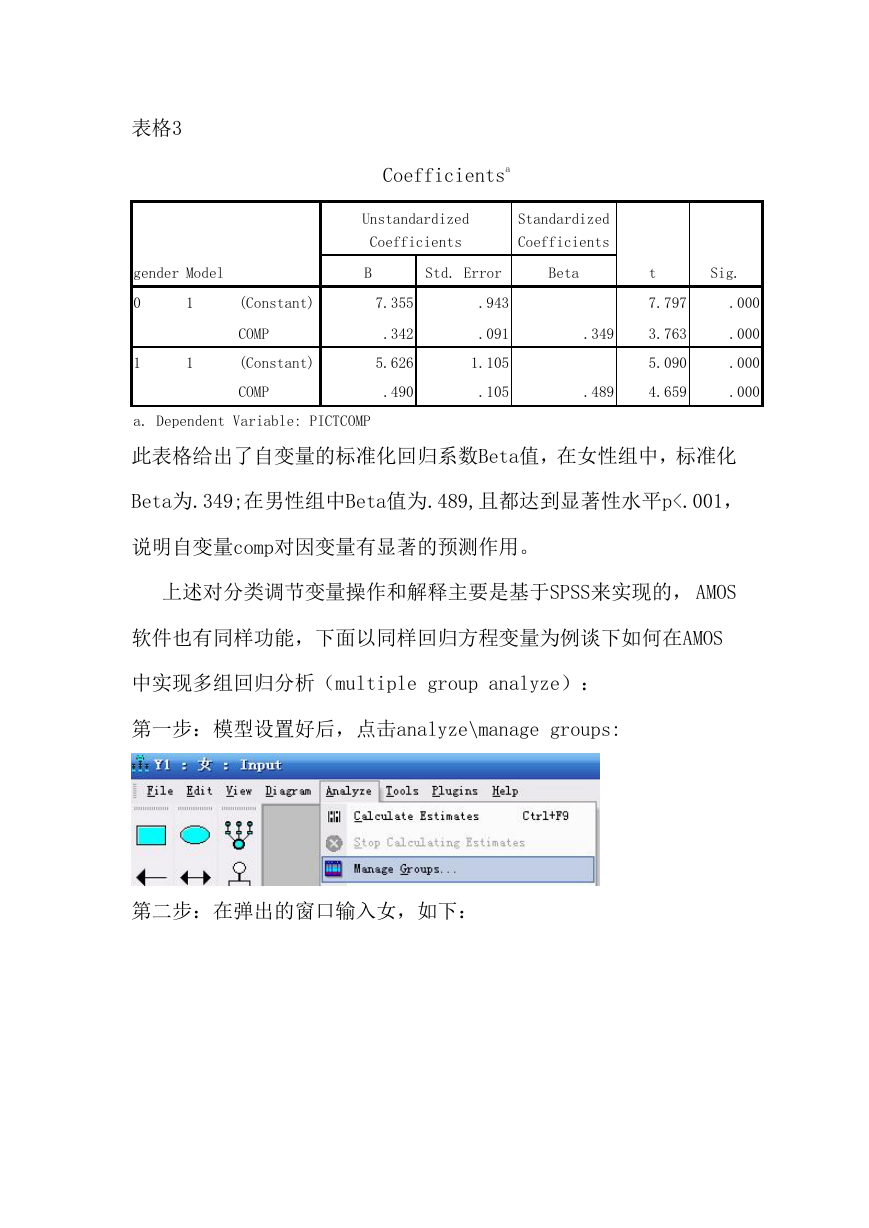
表格3 Coefficientsa Unstandardized Coefficients Standardized Coefficients gender Model B Std. Error Beta t Sig. 0 1 1 1 (Constant) COMP (Constant) COMP 7.355 .342 5.626 .490 .943 .091 1.105 .105 a. Dependent Variable: PICTCOMP 7.797 .349 3.763 5.090 .489 4.659 .000 .000 .000 .000 此表格给出了自变量的标准化回归系数Beta值，在女性组中，标准化 Beta为.349;在男性组中Beta值为.489,且都达到显著性水平p<.001，说明自变量comp对因变量有显著的预测作用。上述对分类调节变量操作和解释主要是基于SPSS来实现的， AMOS 软件也有同样功能，下面以同样回归方程变量为例谈下如何在AMOS 中实现多组回归分析（multiple group analyze）：第一步：模型设置好后，点击analyze\manage groups: 第二步：在弹出的窗口输入女，如下：

资料库

spss中介调节实际操作.doc

相关推荐

课程资源

热门标签

最新资料