论文研究-基于等距分布的球麦克风阵列三维空间声源检测与定位 .pdf-资料库

weixin_39840515-11547404-4744302543018616434.pdf-第1页.png

第1页 / 共7页

weixin_39840515-11547404-4744302543018616434.pdf-第2页.png

第2页 / 共7页

weixin_39840515-11547404-4744302543018616434.pdf-第3页.png

第3页 / 共7页

weixin_39840515-11547404-4744302543018616434.pdf-第4页.png

第4页 / 共7页

weixin_39840515-11547404-4744302543018616434.pdf-第5页.png

第5页 / 共7页

weixin_39840515-11547404-4744302543018616434.pdf-第6页.png

第6页 / 共7页

weixin_39840515-11547404-4744302543018616434.pdf-第7页.png

第7页 / 共7页

基于等距分布的球麦克风阵列三维空间声源检测与 http://www.paper.edu.cn 定位汤永清方勇黄青华上海大学通信学院，上海，200072 E-mail：yfang@shu.edu.cn 摘要：三维(3D)音频需要获得声源的空间方位信息。文章将声场表示成各球谐波的线性组合，对其进行球傅里叶变换，利用球谐波的正交特性，在空间坐标中搜索声源，找出最大值并定位出声源的空间位置。文章中给出了球麦克风的等距离分布算法。所设计的球麦克风阵列的声压用 NI 仪器采集后，进行了数值仿真。实验表明，该方法能获得声源的准确方位，并且运算量小，所需的麦克风数量远远小于其他分布。关键词：3D 音频球麦克风阵列球谐波声源检测声源定位中图分类号：TN912 1. 引言麦克风阵列是为了获得声源的信息，由一系列麦克风按不同的几何形状布置而成的，它广泛应用于声场分析、语音增强以及声源定位等。根据应用背景的不同，对阵列的几何形状以及麦克风数量的选择上具有不同的侧重点。比如在语音增强算法中，对于阵列的形状并不讲究，而主要是关注麦克风阵列的数量；在声场采集中，为获得高分辨率的声场信息，需要同时关注麦克风的数量与几何形状；在声源定位中，阵列的几何形状对于算法的选择性最有十分重要的作用[1]。常见的几何形状有线性、圆形、面阵、非规则形、球形等。等间隔线性与圆形阵列因其结构简单及良好的对称性而获得广泛应用。 3D 音频需要从空间中检测到声源的方位信息，重发端利用方位信息进行声场的重新绘制以达到自然声源的效果。这为下一代立体电视的音频系统提供了理论基础。本文就是基于该应用背景而展开的研究。采用球形麦克风阵列进行声场录制，不仅可以准确获取声源的方位信息，还能保留高阶的声场信息，为下一步的声场重新绘制提供了高保真的信源。由于球形麦克风阵列本身结构的特殊性，在波束形成，3D 音频、高阶声场录制等领域有着良好的应用前景，近年来，逐渐成为研究热点。用球麦克风阵列对所形成的声场进行空间采样，类似于时域采样，需要避免出现混叠，这就对麦克风阵列的设计提出要求。如麦克风在球上如何分布、需要的麦克风数量等问题。利用球麦克风阵列的对称性用于声源定位，与传统的声源定位方法不一样，不同直接对阵列的输出信号进行处理，而是将声场进行球谐波函数分解，并充分利用球谐波函数的正交性，简化运算，从而定标出声源的位置。文章组织如下：第二节介绍了球傅里叶变换以及在刚性球表面所形成的声场；接下来论述了声源检测与定位的策略；第四部份讨论了球等距离分布设计思路；第五节利用等距离分布在声源定位中的应用。最后对全文进行了总结。 2. 球傅里叶变换及声场分析根据文献[2]，对于能量有限的实值函数，其球傅里叶变换对可以表示为：本课题得到上海市科委自然科学基金资助(NO. 08ZR1408300) 1

f ( Ω = ) n ∞ ∑ ∑ n = 0 m n =− f Y m * nm n ( Ω ) f nm = ∫ f ( Ω Y ) m n ( Ω d ) Ω http://www.paper.edu.cn （1 ）（2）其中 nmf 为球傅里叶系数, ( 在球坐标系中傅里叶系数又可以表示为： ( , )θφ Ω = ) 表示球坐标。 π sin 2 πθ ∫ 0 ∫ 0 f ) ( ( nm = Ω Ω d φ Y ) m n f 当平面波入射到硬边界面时，即球由刚性物质所组成[3]，球表面所形成的声场可以表示为入射波声场与反射波声场的叠加。由声场欧拉方程可知，一个声场是由所形成的声压以及声场中相应的粒子速度所决定的。由于是刚性球，在球表面处粒子的速度为 0，故该点的声场可以由该点处的声压唯一决定。（3）入射声场为： p i ( Ω = ) n ∞ ∑ ∑ n = 0 m n =− n i 4 π j ka D n ( ) ( Ω nY ) m 0 ( Ω ) （4）其中 D Ω ( ) 0 是入射角相关的函数，称为方位因子。 D ( Ω = ) 0 * Y m n ( Ω 0 ) a。为刚性球半径， ) nj ka 为 n 阶球 Bessel 函数，Y 表示球谐波函数， 0 ( 坐标形式。（如图 1 所示）。 ( Ω = ) ( , 0)θ φ 0 表示平面波入射角的球 Ω φ θ 图 1 球坐标示意图由球反射的声场为： p s ( Ω = ) n ∞ ∑ ∑ n = 0 m n =− i 4 π − n j ka ( ) ' n ka h ( ' (2) n ) h n (2) ( ka D ) ( Ω nY ) m 0 ( Ω ) （5）其中 nh (2)( ka ) 为二类球 Hankel 函数。 nj ka ' ( ) ， nh (2)' ( ka ) 分别为球 Bessel 函数和球二类 Hankel 函数的一阶导数，。因此：声场可以描述为： p ) Ω = Ω + Ω p ( ) ( ( ) p i s 2

http://www.paper.edu.cn ( Ω Y ) m n 0 ( Ω ) （6 ） b kr ka D n ( ) , p ( Ω = ) n ∞ ∑ ∑ n = 0 m n =− 其中 b kr ka n ( , ) i π= 4 n ( j kr n ( ) − j ka ' n h ka ' n ( ( ) ) h kr n ( )) 称为模态强度。因为此数所测量的是在球表面的值， r a= ,故表示成 ka 的函数，关于此参数的详细说明可以参阅文献 nb [5][6][8]。其离散形式为： p N ( Ω = ) j n N ∑ ∑ n = 0 m n =− b kr D n ( ) ( Ω Y ) m n ( Ω j 0 ) p nm = S ∑ j 1 = w p j N ( Ω Y ) m * n ( )Ω j j （7 ）（8 ）其中指所采样的阶数，为采样麦克风的个数， N S jw 为第 j 个麦克风的补偿加权值。 3. 声场检测及定位利用球麦克风阵列去进行声源定位，将声场描述成各阶球谐波的线性组合，对声场进行球傅里叶变换。利用球谐波的正交特性，在空间坐标中搜索声源，找出幅度最大值并定位出声源的空间位置。 ∫ p p 0 b kr Y )* m n n Ω Ω = Ω = Y m n (9) )* kr Ω Ω d mn ( ) ( ( ) ( ( ) , * 0 * 0 j j j 当空间存在着若干个声源时，并令其幅度密度为 ( a kr Ω , 0) 0 , ( ) ( d Ω a kr ) ( Ω Ω = b kr Y ) m * n n ∫ 又由和的积分等于积分的和，对若干个声源所形成的声压做球傅里叶变换，可得： p lmn Ω = Ω Ω Ω = b kr )* ( n b kr n b kr n a nm Y m * n )* )* )* kr kr D Ω = p d a nm ( ( ) ( ( ) ( ( ) ( ) , 0 0 0 0 j j j (10) (11) ∫ 再由反变换可得： A kr N ( , Ω = ) n N ∑ ∑ n m n 1 = =− 1 b kr ( n ) S ∑ j 1 = p N ( Ω w Y ) m * j n ( Ω j Y ) m n j ( Ω ) (12) 经反变换得到的 NA kr Ω ( , ) 就是声源在整个空间中幅度密度的分布情况，存在着声源的方位最大值，根据这个原理，可寻找其最大值所对应的坐标，即为声源的方位。 4. 等距离球节点分布算法文献[4]指出，对球上麦克风的布置可以有不同的方案。从效率的角度，对于采样阶数为 N ,等角度分布所需的麦克风总数 1)N≥ 4( + ，高斯分布所需的麦克风总数 2 3 1)N≥ 2( + 2 ，

而等距离方案只需用麦克风数为 1)N≥ + ( http://www.paper.edu.cn 2 。比如：对于 4 阶采集，使用等角度分布需要麦克风数量为 100 个，用高斯分布需要 50 个，而采用等距离分布只需 25 个。但是该文献并没有给出如何寻找满足条件的节点。构造代价函数： E x x , 2 ( 1 ,... x N ) = N N ∑ ∑ i 1 = j i 1 = + 1 − || x i x j || 2 （13） sin sin , cos φ θ i i r i ) i θ ，并令为单位球，取 ir = 1 ，其中 || ||• 2 表示欧式空间范数利用球坐标展开， x i = r ( cos i sin , φ θ i i r i 代入上式方程，可得： E i i ( φ θ , ) N N = ∑ ∑ i 1 = j i 1 = + d , ( ) φ θ φθ i i , , j j 其中 d φ θ φ θ = ( , ) , , i i j j [(cos φ θ i i sin − cos φ θ j sin j 2 ) + (sin sin φ θ i i − sin φ θ j sin j 2 ) + (cos θ i − 至此，对球坐标的求解就转化为有约束非线性方程的优化问题。 cos ) ] 2 ( 1/ 2) θ − j min( N N ∑ ∑ i 1 = j i 1 = + d φθ φ θ ( j , , , i i j )) 满足： 0 0 ≤ ≤ 2 ≤ φ π i θ π ≤ i (1 (1 i N ≤ ≤ i N ) ≤ ≤ ) （14）取阶数为 4，麦克风总点数取为 ( 1)N + 2 =25，其在球上的角度分布如表 1 所示。表 1 等距离球节点分布 4 阶 25 点(单位：角度) θ1-5 φ1-5 θ6-10 φ6-10 θ11-15 φ11-15 θ16-20 φ16-21 θ21-25 φ21-25 0 47 100 41 77 0 0 245 110 279 50 72 83 129 82 240 144 96 83 326 165 115 103 80 124 19 292 171 206 29 112 91 148 50 125 127 55 262 54 338 150 126 87 41 44 153 209 9 301 181 4

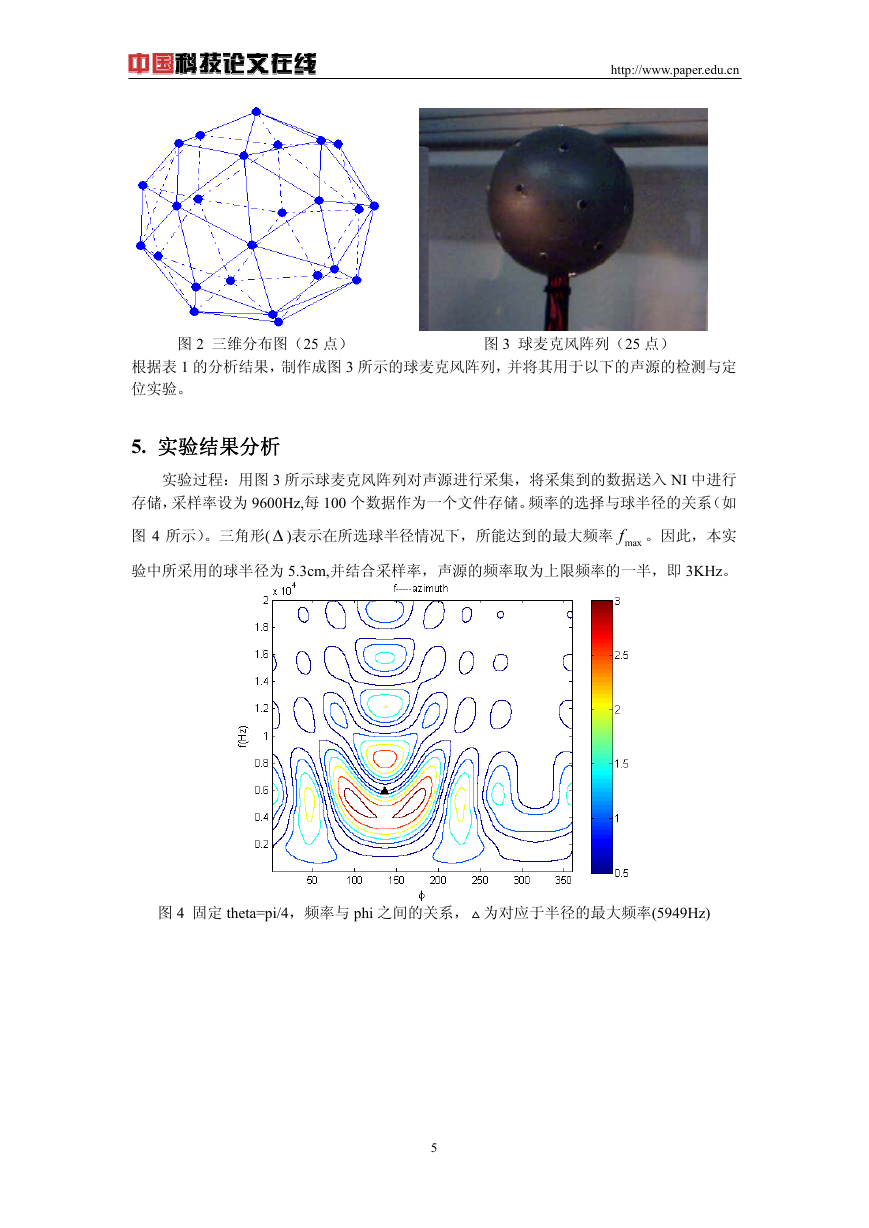
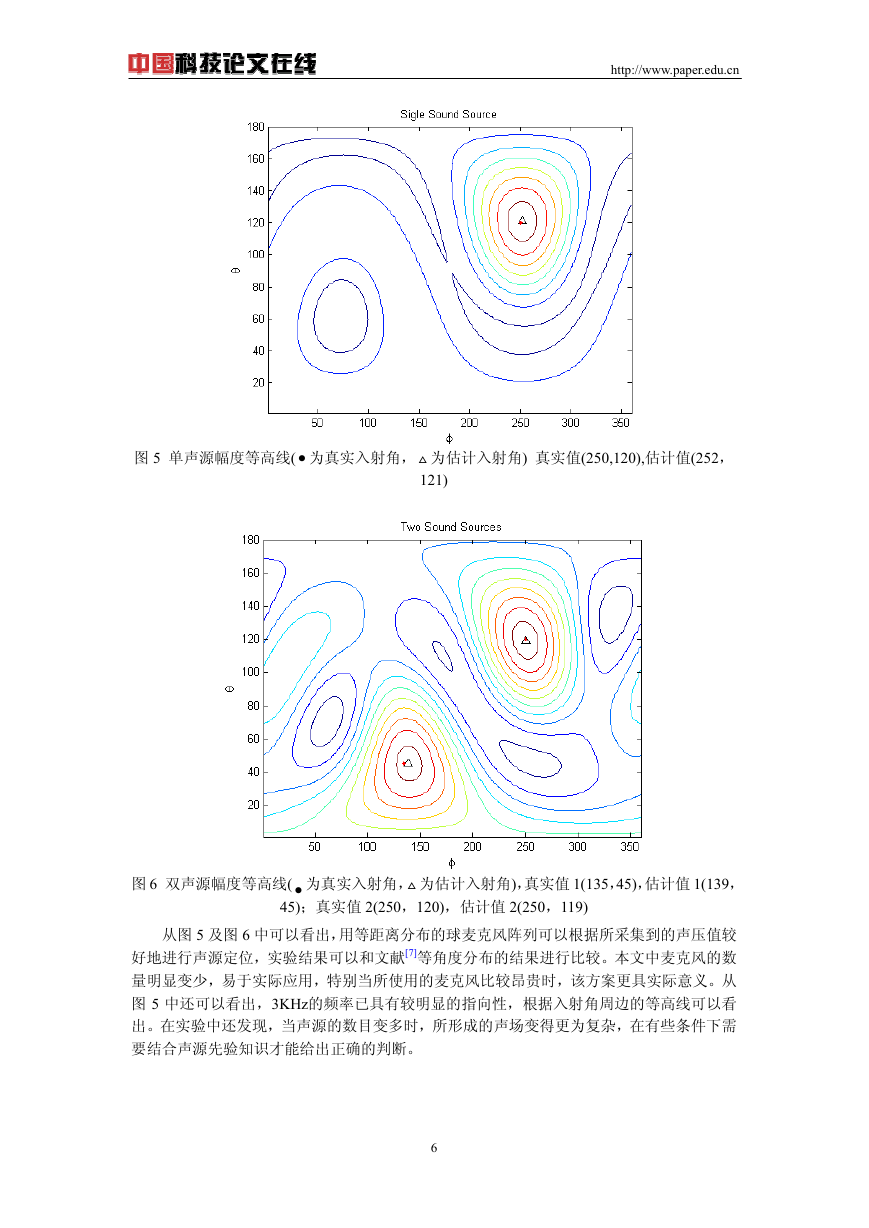
http://www.paper.edu.cn 图 2 三维分布图（25 点）图 3 球麦克风阵列（25 点）根据表 1 的分析结果，制作成图 3 所示的球麦克风阵列，并将其用于以下的声源的检测与定位实验。 5. 实验结果分析实验过程：用图 3 所示球麦克风阵列对声源进行采集，将采集到的数据送入 NI 中进行存储，采样率设为 9600Hz,每 100 个数据作为一个文件存储。频率的选择与球半径的关系（如 f 。因此，本实 max )表示在所选球半径情况下，所能达到的最大频率图 4 所示）。三角形( Δ 验中所采用的球半径为 5.3cm,并结合采样率，声源的频率取为上限频率的一半，即 3KHz。图 4 固定 theta=pi/4，频率与 phi 之间的关系，为对应于半径的最大频率(5949Hz) 5

http://www.paper.edu.cn 图 5 单声源幅度等高线( 为真实入射角，为估计入射角) 真实值(250,120),估计值(252， • 121) 图 6 双声源幅度等高线( 为真实入射角，为估计入射角)，真实值 1(135，45)，估计值 1(139， • 45)；真实值 2(250，120)，估计值 2(250，119) 从图 5 及图 6 中可以看出，用等距离分布的球麦克风阵列可以根据所采集到的声压值较好地进行声源定位，实验结果可以和文献[7]等角度分布的结果进行比较。本文中麦克风的数量明显变少，易于实际应用，特别当所使用的麦克风比较昂贵时，该方案更具实际意义。从图 5 中还可以看出，3KHz的频率已具有较明显的指向性，根据入射角周边的等高线可以看出。在实验中还发现，当声源的数目变多时，所形成的声场变得更为复杂，在有些条件下需要结合声源先验知识才能给出正确的判断。 6

http://www.paper.edu.cn 6. 总结利用球麦克风进行声源定位，充分利用了球的特殊性与对称性，以及球谐波函数的正交性，可以有效地简化算法，为空间声源定位提供了新的思路。但是对于声源定位的研究还有一些问题需要解决：比如相干声源的相互干扰，可能会对声源的定位产生不确定的因素；因为球麦克风是离散布置的，在空间分辨率内的不同声源的定位也存在着一定的模糊性，再者就是声源个数的确定问题，在上述实验过程中，都不自然地用了一些先验的知识，假设声源个数是已知的。这些都是下一步需要研究的课题。参考文献 [1] Benesty J, Chen J, Huang Y. Microphone array signal processing [M].Berlin: Springer, 2008 [2] E.G Williams. Fourier acoustic: Sound radiation and near-field acoustical holography [M]. New York: Academic, 1999 [3].杜功焕，朱哲民，龚秀芬. 声学基础[M]. 南京:南京大学出版社. 2001（第二版）. [4].Boaz R. Analysis and design of spherical microphone array [J]. IEEE Transactions on Speech and Audio Processing, Vol.13, NO.1, pp.135-143, January 2005 [5].Dmitry N, Ramani D, Nail A. Sound field decomposition using spherical microphone arrays [C].Proc. IEEE ICASSP 2008,pp.277-280 [6].Li ZY, Ramani D. Flexible and optimal design of spherical microphone arrays for beam forming [J]. IEEE Transactions on Speech and Audio Processing, Vol.15, NO.2, pp.702-713, February 2007 [7].Lin ZB, Xu BL. Three-dimensional localization of multiple acoustic sources using spherical microphone array [J]. Journal of Nanjing University (Natural Sciences), Vol. 42, NO.4, pp. 384-393.July, 2006 Vol.16, NO.4, pp.740-743, May 2008 [8]. Boaz R. The spherical-shell microphone array [J]. IEEE Transactions on Audio and Language Processing, Detection and Location of Sound Sources Based Spherical Microphone Array with Equidistance in Three-Dimension Tang Yongqing Fang Yong Huang Qinghua Institute of Communication& Information Engineering, Shanghai University, Shanghai, 200072 Abstract: Three-Dimension (3D) audio need to acquire sound sources’ location information. In this paper, sound pressure was express as linear combination of different orders’ spherical harmony, and was transformed by spherical Fourier. The amplitude maximum searched in three dimension is location of sound source using spherical harmony’s orthogonality. The paper also provided algorithm on equidistance distributed. The sound pressure on microphone array was recorded by NI instruments and simulated. The experiments demonstrated that the array with equidistance work well used for location with small computation, and the number of microphone is less than other distributions. Key words: 3D audio, spherical microphone array, spherical harmony, sound detection, sound location 作者简介：汤永清(1974- )，博士生，研究方向：阵列信号处理，3D 音频。方勇(1964- ) ，教授，博导，研究方向：盲信号处理、通信信号处理和智能信息系统。 7

资料库

论文研究-基于等距分布的球麦克风阵列三维空间声源检测与定位 .pdf

相关推荐

开发技术

热门标签

最新资料