泊松过程样本轨道的 MATLAB 仿真 一、 Poisson Process 定义 { 若有一个随机过程 N  : N t t  是参数为λ>0 的 Poisson 过程，它满足下列条件： 0} 1、 0N = 0； 2、对任意的时间指标0   ，增量  N t s t    N s    服从参数为 s    t 泊松分布。 3、对任意的自然数 n≥2 和任意的时间指标    N t 0 t 0 N N        ，n 个增量 , t 1 N  t 2 n t 1 t 1 t 0 N t n , t n 1  N t 2 是相互独立的随机变量。 二、从泊松过程的定义可知 1、泊松过程具有平稳独立增量性。 2、时间指标集合为[ 0 , +∞],状态空间为 S=N 。 3、泊松过程是一个连续时间离散状态的随机过程。 * 三、MATLAB 仿真泊松过程的思想 1、若定义 iT 为泊松过程的到达时间，   n T n   1 , T n n   为到达时间间隔。那么泊松 过程 N 的到达时间间隔{ : n n N   是相互独立且同服从于参数为λ的指数分布。 } 2、若 U 是服从于[0，1]的均匀分布，则 E   1  ( Ln U ) 服从于参数为λ的指数分布。利用随机变量分布函数的定义很容易证明这条性质。 3、由于 1、和 2、中的条件成立，现在我们考虑 1    n T n T n   1   Ln U n ( )] [ 那么就可以推出 T n   1 T n  1  Ln U n ( )] [ 在 MATLAB 中我们可以用 rand(1,K)产生一个具有 K 个值的随机序列，它们在[0,1]上 服从于均匀分布，利用上式计算出 nT ，在每一个到达时间 nT 处， N 的值从 n-1 变成 n。 用 plot 函数就可以将样本轨道画出了。 四、MATLAB 程序 1、首先我们建立一个 poisson 函数，即 poisson.m: function poisson(m) %This function can help us to simulate poisson processes. %If you give m a integer like 1 2 3 and so on ,then you will get %a figure to illustrate the m sample traces of the process. % rand('state',0); %复位伪随机序列发生器为0状态 K=10; %设置计数值为10 

%m=6; %设置样本个数 color=char('r+','b+','g+','m+','y+','c+'); %不同的轨道采用不同的颜色表示 lambda=1; %设置到达速率为1 for n=1:m u=rand(1,K); %产生服从均匀分布的序列 T=zeros(1,K+1); %长生K+1维随机时间全零向量 k=zeros(1,K+1); %产生K+1维随机变量全零向量 for j=1:K k(j+1)=j; T(j+1)=T(j)-log(u(j))/lambda; %计算到达时间 end for i=1:K plot([T(i):0.001:T(i+1)],[k(i):k(i)],color(n,[1,2])); hold on; end end 2、下面我们在命令窗口键入以下命令： clear； poisson(1); 就可以得到一条样本轨道，如下所示： 

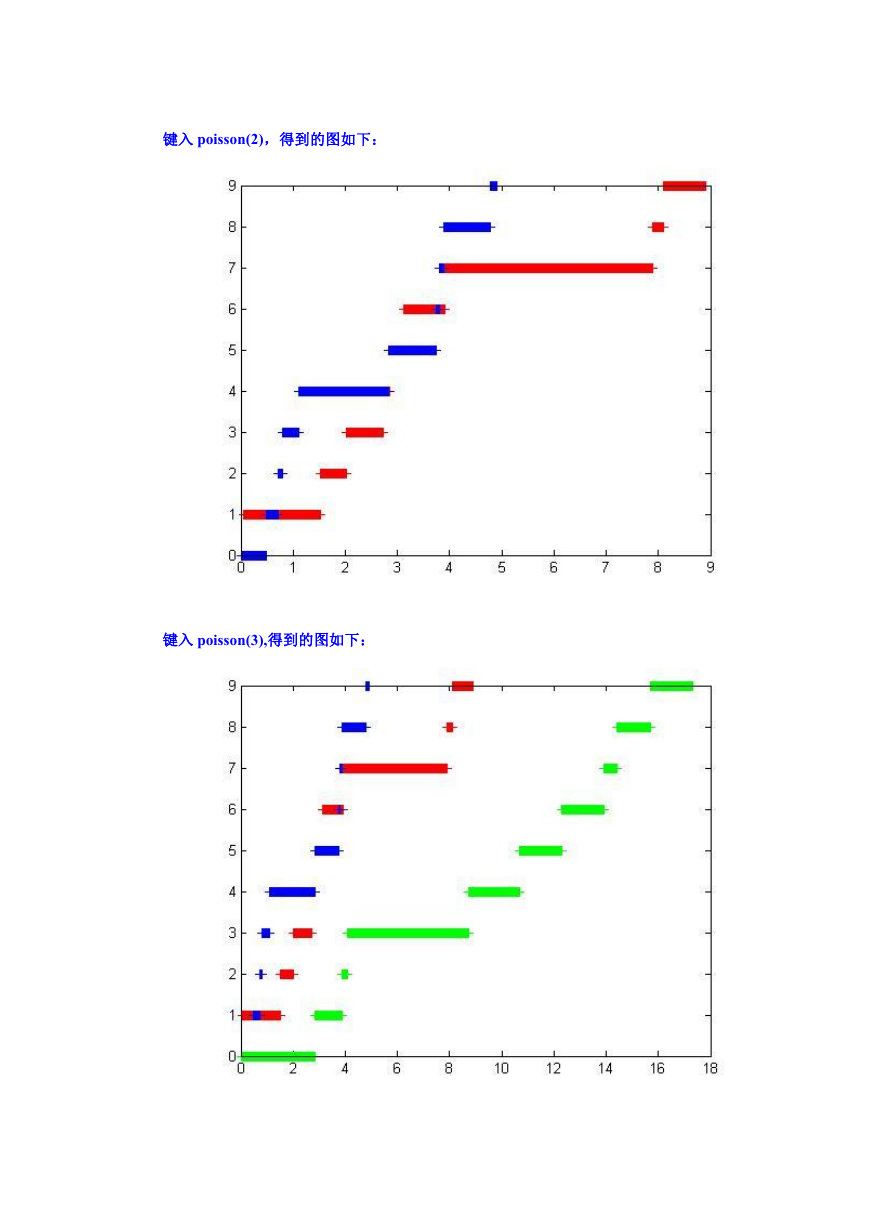
键入 poisson(2)，得到的图如下： 键入 poisson(3),得到的图如下： 

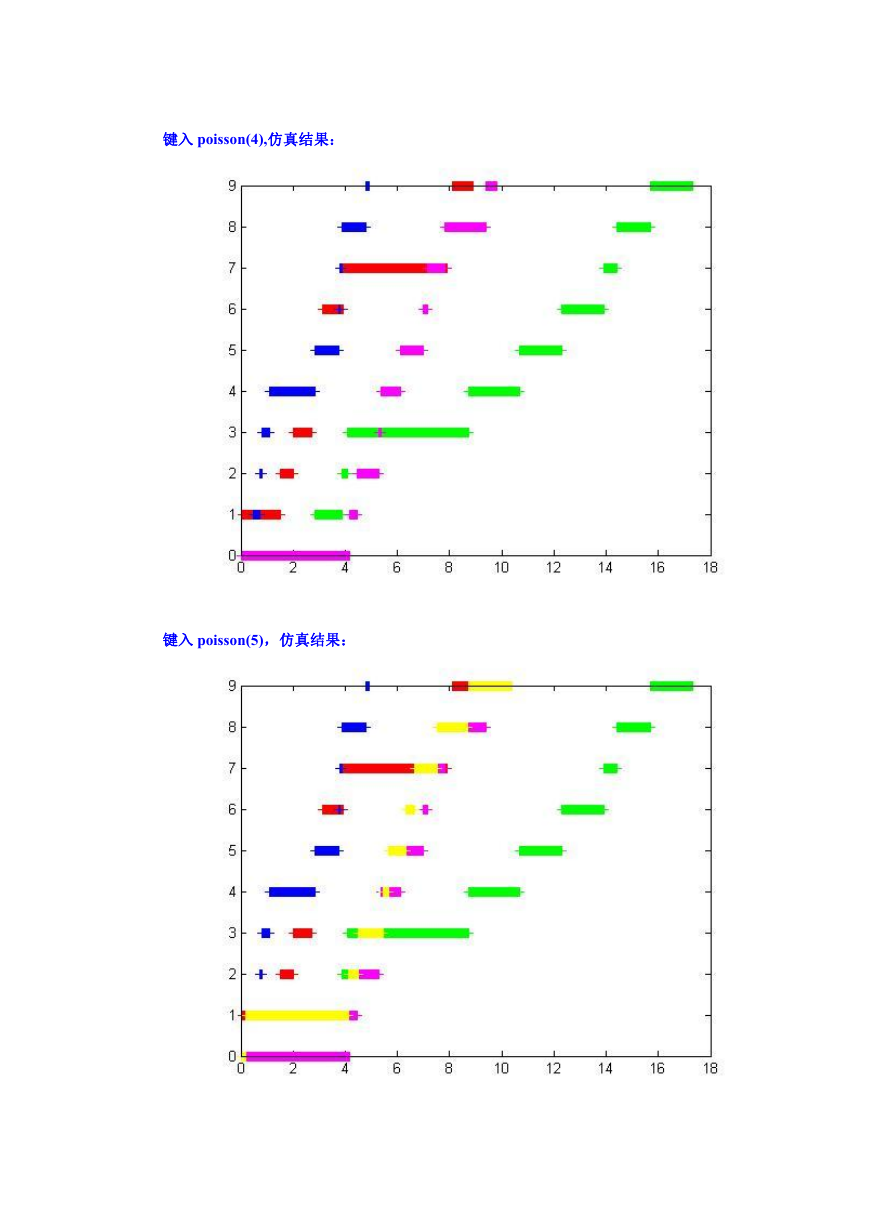
键入 poisson(4),仿真结果： 键入 poisson(5)，仿真结果： 

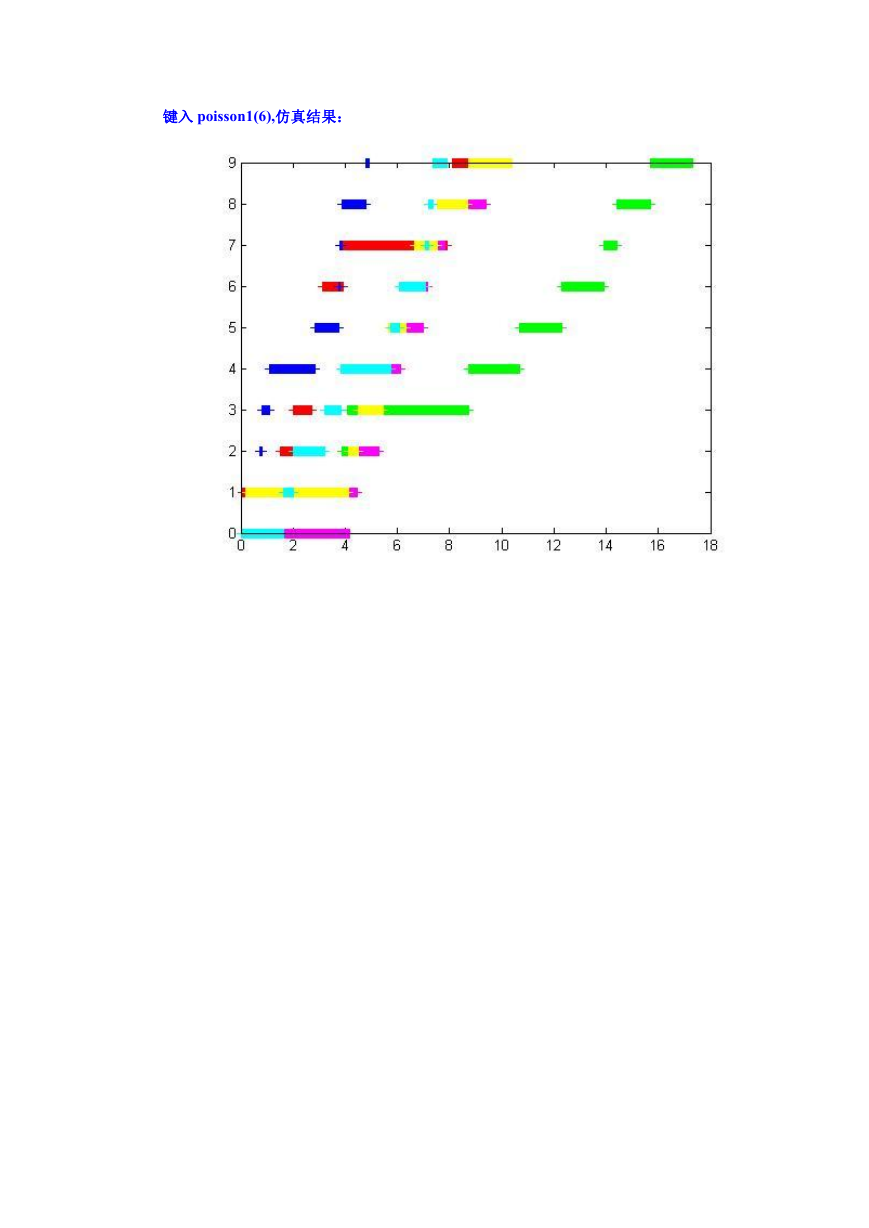
键入 poisson1(6),仿真结果：