logo资料库

DNL INL的计算.doc

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.29M 资料格式：doc 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
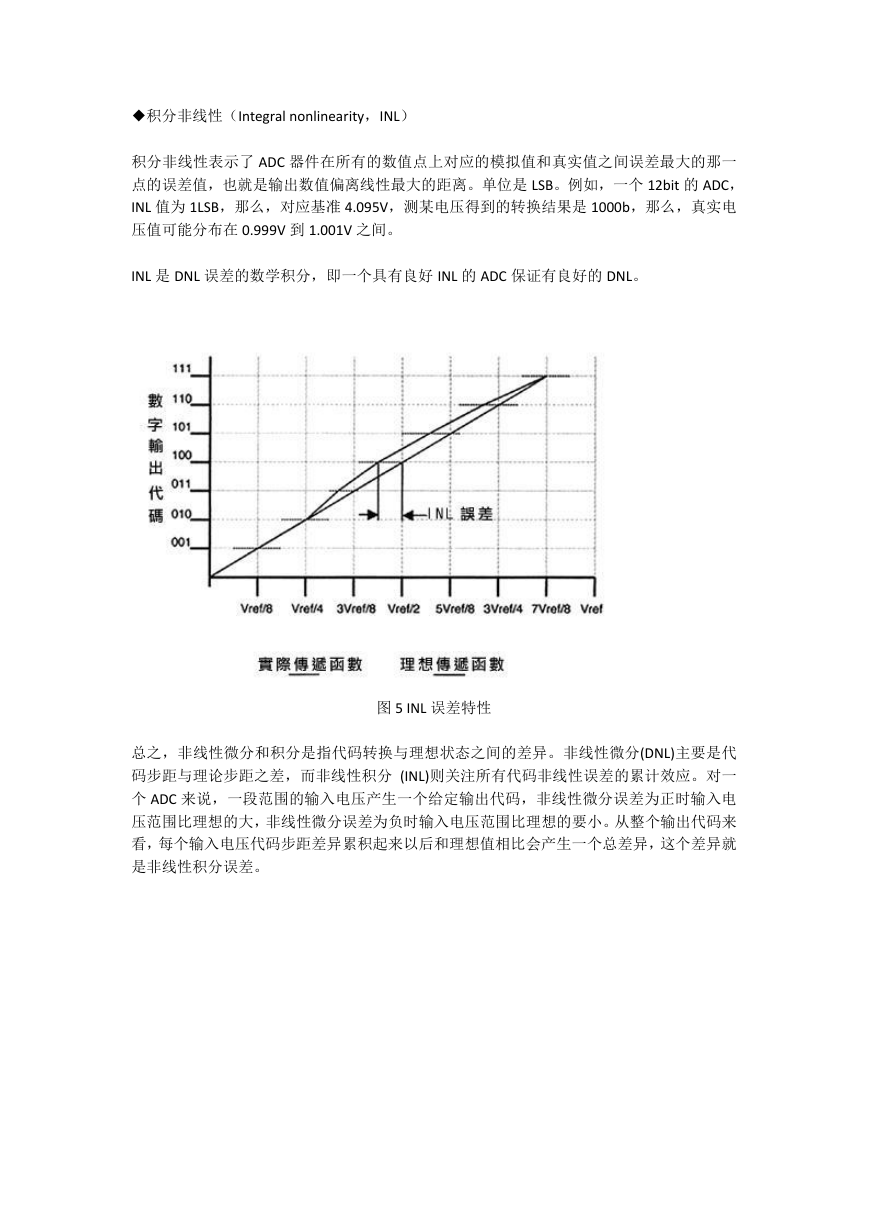
    ◆积分非线性（Integral nonlinearity，INL） 积分非线性表示了 ADC 器件在所有的数值点上对应的模拟值和真实值之间误差最大的那一 点的误差值，也就是输出数值偏离线性最大的距离。单位是 LSB。例如，一个 12bit 的 ADC， INL 值为 1LSB，那么，对应基准 4.095V，测某电压得到的转换结果是 1000b，那么，真实电 压值可能分布在 0.999V 到 1.001V 之间。 INL 是 DNL 误差的数学积分，即一个具有良好 INL 的 ADC 保证有良好的 DNL。 图 5 INL 误差特性 总之，非线性微分和积分是指代码转换与理想状态之间的差异。非线性微分(DNL)主要是代 码步距与理论步距之差，而非线性积分 (INL)则关注所有代码非线性误差的累计效应。对一 个 ADC 来说，一段范围的输入电压产生一个给定输出代码，非线性微分误差为正时输入电 压范围比理想的大，非线性微分误差为负时输入电压范围比理想的要小。从整个输出代码来 看，每个输入电压代码步距差异累积起来以后和理想值相比会产生一个总差异，这个差异就 是非线性积分误差。
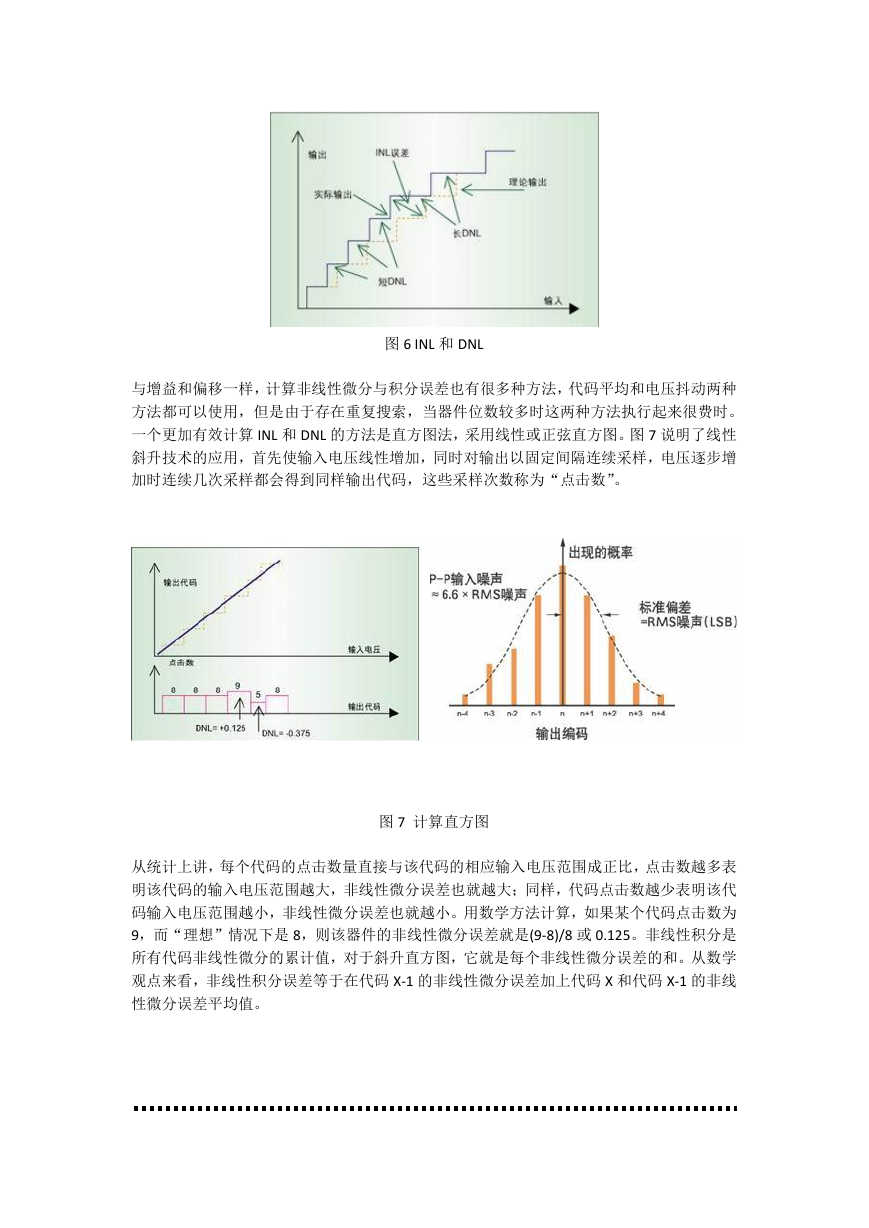
    图 6 INL 和 DNL 与增益和偏移一样，计算非线性微分与积分误差也有很多种方法，代码平均和电压抖动两种 方法都可以使用，但是由于存在重复搜索，当器件位数较多时这两种方法执行起来很费时。 一个更加有效计算 INL 和 DNL 的方法是直方图法，采用线性或正弦直方图。图 7 说明了线性 斜升技术的应用，首先使输入电压线性增加，同时对输出以固定间隔连续采样，电压逐步增 加时连续几次采样都会得到同样输出代码，这些采样次数称为“点击数”。 图 7 计算直方图 从统计上讲，每个代码的点击数量直接与该代码的相应输入电压范围成正比，点击数越多表 明该代码的输入电压范围越大，非线性微分误差也就越大；同样，代码点击数越少表明该代 码输入电压范围越小，非线性微分误差也就越小。用数学方法计算，如果某个代码点击数为 9，而“理想”情况下是 8，则该器件的非线性微分误差就是(9-8)/8 或 0.125。非线性积分是 所有代码非线性微分的累计值，对于斜升直方图，它就是每个非线性微分误差的和。从数学 观点来看，非线性积分误差等于在代码 X-1 的非线性微分误差加上代码 X 和代码 X-1 的非线 性微分误差平均值。
    可以通过用直方图分析的方法 对所采得的数据进行计算，即可以分析静态参数 其实用于 histogram 的输入波形可以是很多种，其中正弦较为常用，我觉得这主要是因为正 弦是一种较容易得到的波形（相对于高度线性的 ramp 而言）。我们对 ADC 输入正弦波，连 续采集大量输出并按输出码分类统计数量，即得到所谓 histogram。 一些数学上的关系如下： 考虑 y=A*sin(x)为输入 ADC 之正弦波形，要取得输出码之 histogram，即相当于在 Y 轴上作等 份并求这些等份所对应的 x 的宽度。取反函数得到 y=arcsin(x/A)，即在 x 轴上作等份处理， 可知对于 X 轴（-A 到 A）上的任一点 x，其在 y 方向上的密度为 1/pi/sqrt(A^2-x^2)，即该点 导数乘一个归一化系数 1/pi。 现考虑 A->2^(N-1)，N 为总的位数，对于前式从 x=n-1 积分至 x=n 即为码 n 的出现概率，有， P(n) = 1/pi*{arcsin[(n-2^(N-1))/2^(N-1)]-arcsin[(n-1-2^(N-1))/2^(N-1)]} 求电压变换点时，有 Vj = A*sin[pi*sigma(P(n=0~j))-pi/2] = -A*cos[pi*sigma(P(n=0~j))] 上面给出的， P(n) = 1/pi*{arcsin[(n-2^(N-1))/2^(N-1)]-arcsin[(n-1-2^(N-1))/2^(N-1)]} 的公式，只是没有 gain/offset 误差的理想情况。如果 ADC 有 gain/offset 误差的话 P(n)的算法 应该是不一样的。 举例来说，如果实际得到的分布是在两个端点上的几率比从上面公式得到的理想情况要大， 即器件实际的峰峰值要比测试时加的小一些。按 DNL 的计算公式， DNL(n) = real_prob(n) / ideal_prob(n) -1 （或者是 real_hit(n)与 ideal_hit(n)，一样的） 此时对于 n=1（假定数组从 1 开始 index）以及 n=2^N，有 real_prob(n) > ideal_prob(n)，而 real_prob 与 ideal_prob 的积分是相同的，这就导致对于 1<2^N 的情况下，普遍有 real_prob(n) < ideal_prob(n)的情况。由于 ideal_prob(n)是两边大中间小的一个澡盆形分布，于是可能有普 遍的 DNL 计算值偏小的这样一种误差，且这些误差的累积是超过两端点上 DNL 计算值偏大 的影响的。正式由于这些误差的积累，导致 DNL 积分得到的 INL 曲线沿着码值向负数方向倾 斜（N 较大时会非常明显）；而且在靠近两端处这种误差不是均匀变化，所以 INL 的曲线会 有扭曲的现象。
    透过现象，问题的关键在于，在上述情况下，实际得到并不是 y=sin(x)的整个值域的分布， 而仅是曲线在 y 轴的中间一部分在 2^N 个点（histogram bin）上的分布。换句话说，原先是 2^N 个点的分布，实际需要 2^N+M 个点才算是 y 的整个值域的分布，这里 2^N 与 2^N+M 的 比值就是器件实际峰峰值与测试时给予的峰峰值的比。 所以在实际操作时，可以故意给予超出器件 Vpp 的正弦波，然后在计算 ideal_prob 的时候， 首先要计算出增益以及零点偏置的误差，把这些因素考虑进去之后，计算的 y=sin(x)的值域 中对应于实际器件输出的那一部分在 2^N-2 个点（两个端点不算）的理论分布。 正弦波直方图法测试 ADC 的 INL/DNL 的方法可能较早是在 M.Mahoney 的 DSP-Based Testing of Analog and Mixed Signal Circuits 一书中提出的，现在已是一个很常规的做法了。在一些国外 的测试方面的书籍中有介绍，如 An Introduction to Mixed Signal IC Test and Measurement，其 12.2.8 节介绍了 Sinusoidal Histogram Method An Introduction to Mixed Signal IC Test and Measurement 这本书国内没有，美国原版要上百美 元。作为学习研究的话或可参考 pdf 版，如 http://bbs.dicder.com/thread-1033-1-1.html 有下载的。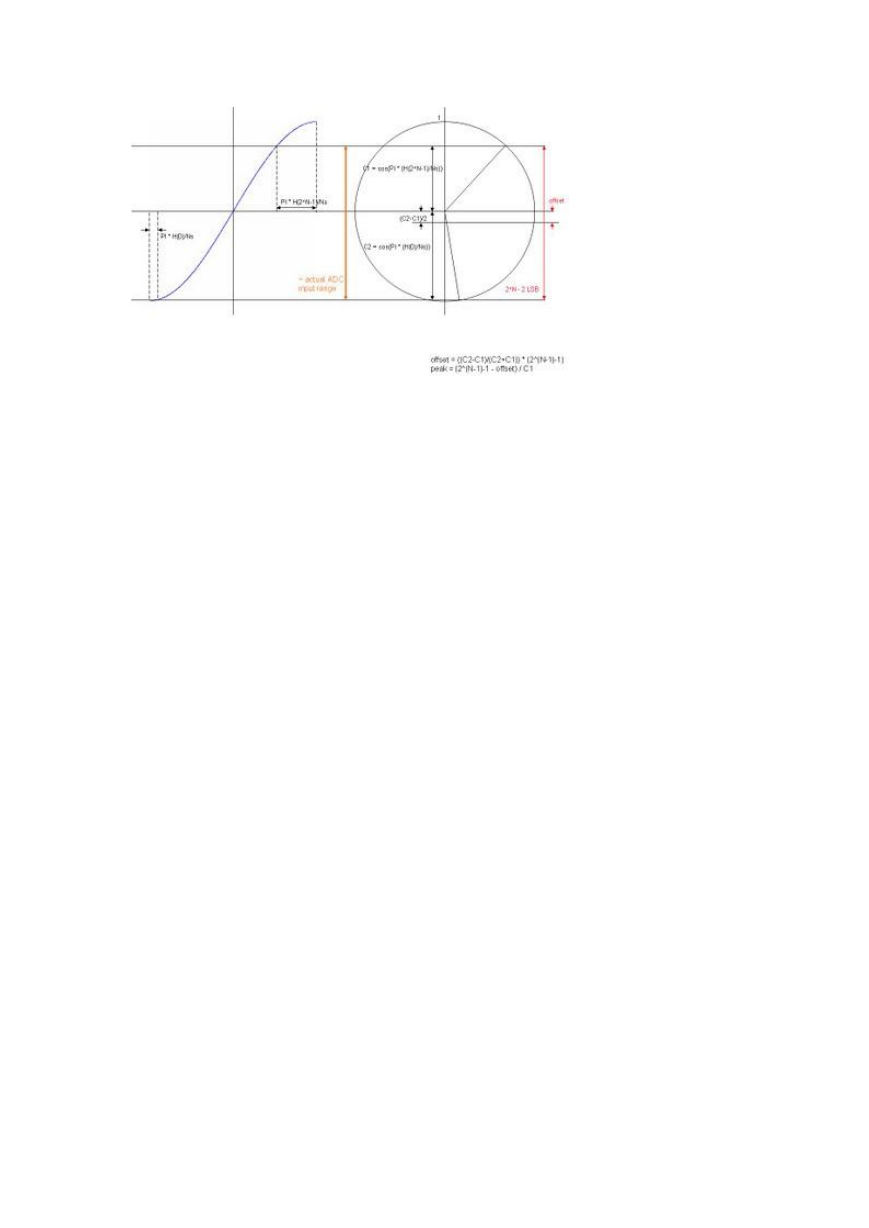 这个算法可以分两部分理解， 一是基本的正弦波条件下各数码的出现概率的基本计算公式，这个在 Maxim 的一份 AN 中有 介绍， http://www.maxim-ic.com.cn/appnotes.cfm/appnote_number/2085/ 二是在此基础上对于 offset/gain(peak)的校正，我下面这张图解释了 offset/peak 的计算。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料