回归分析与拟合MATLAB.pdf

发布时间：2022-06-06 发布人：admin 分类：说明书资料大小：0.25M 资料格式：pdf 举报版权申诉

第1页 / 共16页

qq_33605661-11446597-回归分析与拟合MATLAB.pdf-第2页.png

第2页 / 共16页

qq_33605661-11446597-回归分析与拟合MATLAB.pdf-第3页.png

第3页 / 共16页

qq_33605661-11446597-回归分析与拟合MATLAB.pdf-第4页.png

第4页 / 共16页

qq_33605661-11446597-回归分析与拟合MATLAB.pdf-第5页.png

第5页 / 共16页

qq_33605661-11446597-回归分析与拟合MATLAB.pdf-第6页.png

第6页 / 共16页

qq_33605661-11446597-回归分析与拟合MATLAB.pdf-第7页.png

第7页 / 共16页

qq_33605661-11446597-回归分析与拟合MATLAB.pdf-第8页.png

第8页 / 共16页

数据回归分析和拟合的Matlab实现

一、多元线性回归

代码:

二、多项式回归

代码:

三、非线性回归

代码:

四、逐步回归

代码:

数据回归分析和拟合的 Matlab 实现本次将教程的主要内容包含：一、多元线性回归 2# 多元线性回归：regress 二、多项式回归 3# 一元多项式：polyfit 或者 polytool 多元二项式：rstool 或者 rsmdemo 三、非线性回归 4# 非线性回归：nlinfit 四、逐步回归 5# 逐步回归：stepwise 一、多元线性回归多元线性回归： 1、b=regress(Y, X ) 确定回归系数的点估计值

2、[b, bint,r,rint,stats]=regress(Y,X,alpha) 求回归系数的点估计和区间估计、并检验回归模型 ①bint 表示回归系数的区间估计. ②r 表示残差 ③rint 表示置信区间 ④stats 表示用于检验回归模型的统计量,有三个数值：相关系数 r2、F 值、与 F 对应的概率 p 说明：相关系数 r2 越接近 1，说明回归方程越显著；时拒绝 H0，F 越大，说明回归方程越显著；与 F 对应的概率 p<α 时拒绝 H0 ⑤alpha 表示显著性水平(缺省时为 0.05) 3、rcoplot(r,rint) 画出残差及其置信区间具体参见下面的实例演示 4、实例演示，函数使用说明 (1)输入数据复制内容到剪贴板代码: >>x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]'; >>X=[ones(16,1) x]; >>Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]'; (2)回归分析及检验复制内容到剪贴板代码: >> [b,bint,r,rint,stats]=regress(Y,X) b = -16.0730

0.7194 bint = -33.7071 1.5612 0.6047 0.8340 r = 1.2056 -3.2331 -0.9524 1.3282 0.8895 1.1702 -0.9879 0.2927 0.5734 1.8540 0.1347 -1.5847 -0.3040 -0.0234 -0.4621 0.0992 rint = -1.2407 3.6520 -5.0622 -1.4040 -3.5894 1.6845 -1.2895 3.9459 -1.8519 3.6309 -1.5552 3.8955 -3.7713 1.7955 -2.5473 3.1328

-2.2471 3.3939 -0.7540 4.4621 -2.6814 2.9508 -4.2188 1.0494 -3.0710 2.4630 -2.7661 2.7193 -3.1133 2.1892 -2.4640 2.6624 stats = 0.9282 180.9531 0.0000 1.7437 运行结果解读如下参数回归结果为，对应的置信区间分别为[-33.7017,1.5612]和[0.6047,0.834] r2=0.9282(越接近于 1，回归效果越显著)，F=180.9531， p=0.0000，由 p<0.05, 可知回归模型 y=-16.073+0.7194x 成立 (3)残差分析作残差图复制内容到剪贴板代码: rcoplot(r,rint) 二、多项式回归一元多项式回归 1、一元多项式回归函数

(1)[p,S]=polyfit(x,y,m) 确定多项式系数的 MATLAB 命令说明：x=(x1,x2,…,xn),y=(y1,y2,…,yn)；p=(a1,a2,…,am+1)是多项式 y=a1xm+a2xm-1+…+amx+am+1 的系数； S 是一个矩阵,用来估计预测误差 (2)polytool(x,y,m) 调用多项式回归 GUI 界面，参数意义同 polyfit 2、预测和预测误差估计 (1)Y=polyval(p,x) 求 polyfit 所得的回归多项式在 x 处的预测值 Y (2)[Y,DELTA]=polyconf(p,x,S,alpha) 求 polyfit 所得的回归多项式在 x 处的预测值 Y 及预测值的显著性为 1-alpha 的置信区间 Y±DELTA，alpha 缺省时为 0.5 3、实例演示说明观测物体降落的距离 s 与时间 t 的关系，得到数据如下表，求 s 的表达式(即回归方程 s=a+bt+ct2) t (s) 1/30 2/30 3/30 4/30 5/30 6/30 7/30 s (cm) 11.86 15.67 20.60 26.69 33.71 41.93 51.13 t (s) 8/30 9/30 10/30 11/30 12/30 13/30 14/30 s (cm) 61.49 72.90 85.44 99.08 113.77 129.54 146.48 解法一：直接作二次多项式回归复制内容到剪贴板代码: >>t=1/30:1/30:14/30; >>s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48]; >>[p,S]=polyfit(t,s,2) p = 489.2946 65.8896 9.1329

S = R: [3x3 double] df: 11 normr: 0.1157 故回归模型为解法二：化为多元线性回归复制内容到剪贴板代码: >>t=1/30:1/30:14/30; >>s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48]; >>T=[ones(14,1) t' (t.^2)']; >>[b,bint,r,rint,stats]=regress(s',T) b = 9.1329 65.8896 489.2946 bint = 9.0614 9.2044 65.2316 66.5476 488.0146 490.5747 r =

-0.0129 -0.0302 -0.0148 0.0732 0.0040 0.0474 -0.0165 -0.0078 -0.0363 -0.0222 0.0046 -0.0059 -0.0237 0.0411 rint = -0.0697 0.0439 -0.0956 0.0352 -0.0876 0.0580 0.0182 0.1283 -0.0709 0.0789 -0.0192 0.1139 -0.0894 0.0563 -0.0813 0.0658 -0.1062 0.0335 -0.0955 0.0511 -0.0704 0.0796 -0.0793 0.0675 -0.0904 0.0429 -0.0088 0.0910 stats = 1.0e+007 *

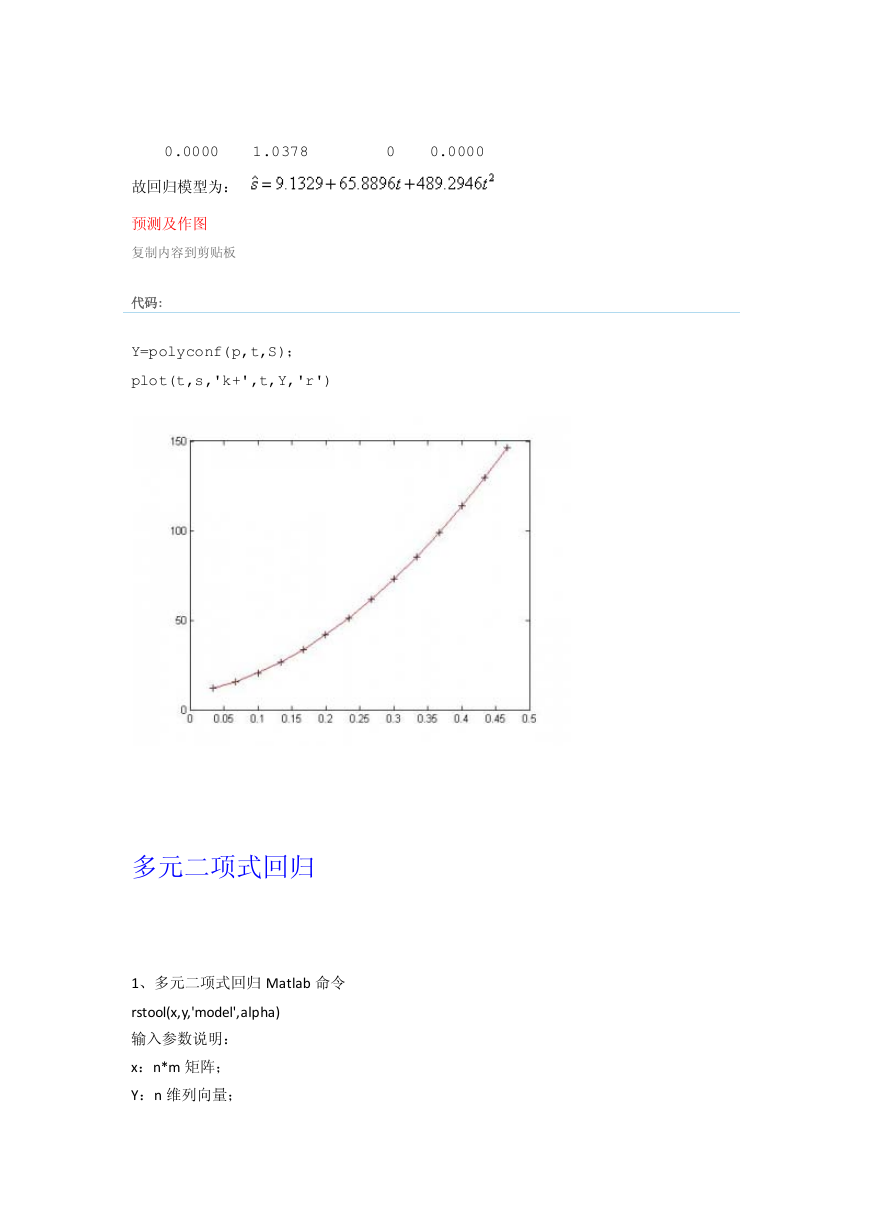
0.0000 1.0378 0 0.0000 故回归模型为：预测及作图复制内容到剪贴板代码: Y=polyconf(p,t,S)； plot(t,s,'k+',t,Y,'r') 多元二项式回归 1、多元二项式回归 Matlab 命令 rstool(x,y,'model',alpha) 输入参数说明： x：n*m 矩阵； Y：n 维列向量；

分享到：

赞收藏

资料库

回归分析与拟合MATLAB.pdf

相关推荐

信息化

热门标签

最新资料