ISSN 1009-3044 第9 卷第21 期 (2013 年07 月) ComputerKnowledgeandTechnology电脑知识与技术 Vol.9, No.21, July 2013. E-mail: eduf@dnzs.net.cn http://www.dnzs.net.cn Tel:+86-551-65690963 65690964 ComputerKnowledgeandTechnology电脑知识与技术 基于DFT、DCT 和小波变换图像压缩与Matlab 实现 张雅琪，才华 （北京邮电大学 北京 , 102209 ） 摘要：简述 DFT、DCT、小波变换原理，并通过 Matlab 模拟 DFT 、DCT、小波变换过程，进而研究了 DCT 、DFT 、小波变 换在图像变换中的差异。通过对比实验结果，得出JPEG 静态图像压缩最佳方案。 关键词：DFT；DCT；小波变换；图像压缩；Matlab 中图分类号：TP391 文献标识码：A 文章编号：1009-3044(2013)21-4929-04 Image Compression Based on DFT、DCT and Wavelet and Realization with Matlab ZHANG Ya-qi，CAI Hua (Beijing University of Posts and Telecommunications, Beijing 102209, China） Abstract：The principle of DFT,DCT,wavelet transformation,.Simulating the process of DFT,DCT and wavelet transformation witn Matlab and then research the differences among DFT,DCT and wavelet transformation.Through the comparison of results , get the best solution to JPEG static image compressed. Key word:DFT; DCT; wavelet transformation; image compressed 随着信息社会的发展，图像作为一种直观的多媒体信息越来越收到重视，如何有效的对图像数据进行压缩也自然成为了研究 的热点。 [1] DCT 目前的图像编码技术种类较多，图像压缩效果也不尽相同。该文通过 和小波变换在图像压缩中的差异，进而选择出图像压缩的最佳方案。 本文其余部分结构如下：第一部分介绍图像压缩技术的现状以及 的实现；第三部分是对图像变换结果的分析。 MATLAB MATLAB MATLAB DFT DCT DFT 实现 、 和小波变换过程，对比 、 相关函数；第二部分介绍了 、 及小波变换 DFT DCT 三种变换原理及 1 背景介绍 1.1 图像压缩技术现状 JPEG 由于 JPEG 标准 面质量，新一代的静止图像压缩标准 1.2 Matlab 及相关函数介绍 MathWorks Matlab 语言是由美国 [3] 。 非常有利 DFT JPEG2000 ', ,[ 1 2 3 (' sh , ]= sh 此次仿真中用到的关键函数： ）imread ：调用方法：imread ）im ）Wavedec ]) type ,' LOW HIGH N 2 DFT 、DCT 、小波变换原理及 Matlab 实现 2.1 DFT 变换原理及 Matlab 实现 ow ：调用方法：im c ：调用方法： file I ow wavedec 2 X ( [ ) 2( , s 具有高效压缩的优势，基于 为核心的静止图像压缩 。近年来，小波变换作为新兴的数学分支正成为图像压缩领域的前沿技术。基于小波的编码有效改进了高压缩比的画 域的图像压缩算法一直很少被使用，国际上制订了以 就以小波变换为核心算法。 DCT 公司推出的计算机软件，其中的数字图像使用矩阵表示，其强大的矩阵运算功能对图像处理 ；功能：根据路径读取图像，并根据图像文件原有格式储存相应的图像矩阵。 [ ] X '), ，功能：根据 wname LOW HIGH 功能：返回矩阵 的设定显示灰度图像。 的一个 层小波分解。 N DFT 变换原理： 离散傅里叶变换 DFT 是傅里叶变换在时域和频域上都呈离散的形式。实际应用中通常采用快速傅里叶变换计算 DFT 下面给出 DFT 及其反变换的变换对： 对于 点序列{ ,DFT 为： N } x[ ]n 0≤ ≤ n N [4] 。 收稿日期：2013-06-15 本栏目责任编辑：唐一东 人工智能及识别技术 4929 

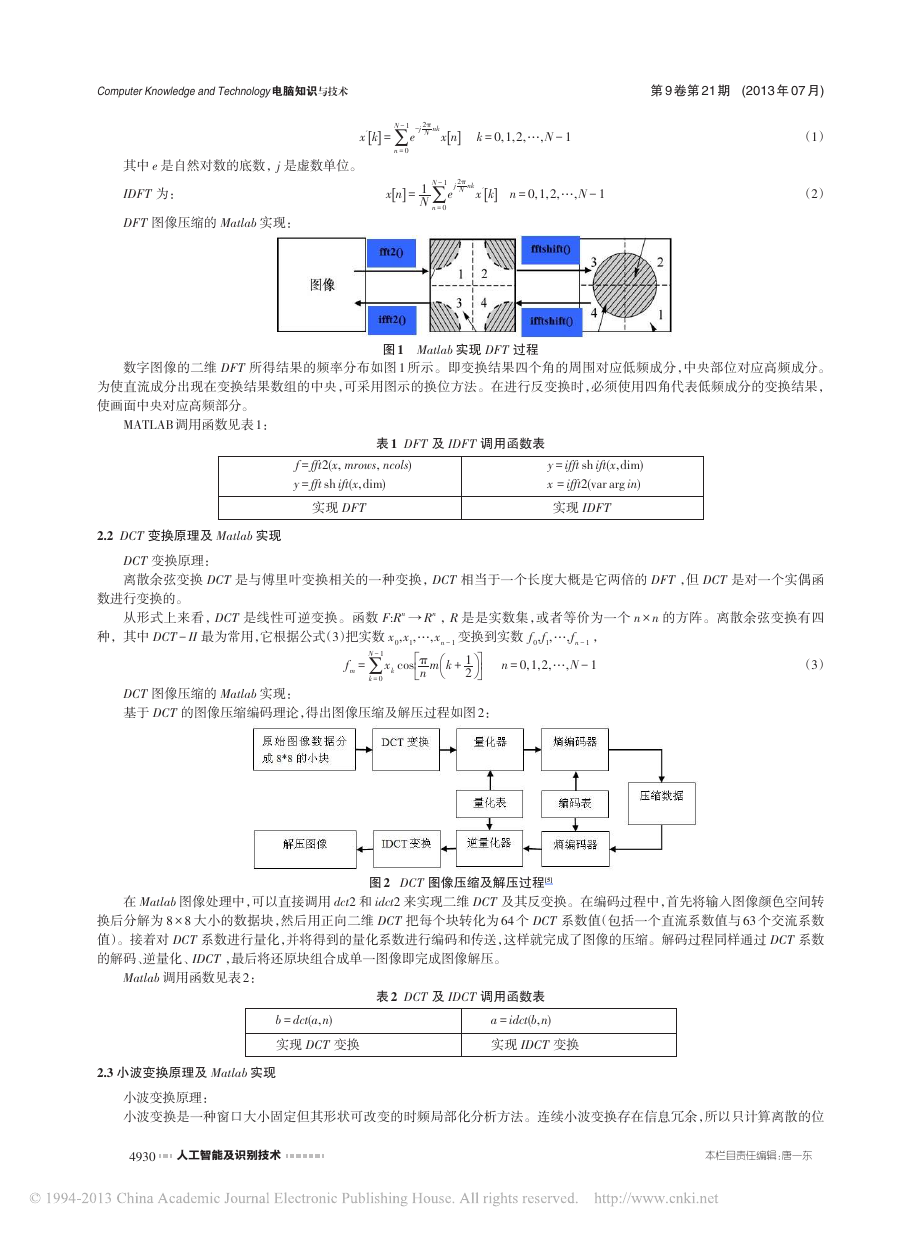
ComputerKnowledgeandTechnology电脑知识与技术 '[ ]k x 其中 e 是自然对数的底数，j 是虚数单位。 IDFT 为： DFT 图像压缩的 Matlab 实现： 2π N j N - e -1 =0 =∑ = 1 n x[ ]n ∑ N -1 =0 N n =0,1,2,…, -1 N nkx[ ]n k 第9 卷第21 期 (2013 年07 月) 1 （ ） 2π N '[ ]k nkx n =0,1,2,…, -1 N 2 （ ） e j 数字图像的二维 DFT 所得结果的频率分布如图 所示。即变换结果四个角的周围对应低频成分，中央部位对应高频成分。 为使直流成分出现在变换结果数组的中央，可采用图示的换位方法。在进行反变换时，必须使用四角代表低频成分的变换结果， 使画面中央对应高频部分。 调用函数见表 MATLAB 1 ： 图1 Matlab 实现 DFT 过程 1 , = = f y fft fft 2( sh x ( mrows ift x ) 表1 DFT 及 IDFT 调用函数表 , ,dim) ncols = = y x ifft ifft ( sh 2(vararg ,dim) ) ift x in 2.2 DCT 变换原理及 Matlab 实现 实现 DFT 实现 IDFT DCT 变换原理： 离散余弦变换 DCT 是与傅里叶变换相关的一种变换，DCT 相当于一个长度大概是它两倍的 DFT ，但 DCT 是对一个实偶函 数进行变换的。 - 种，其中 DCT II 最为常用，它根据公式（ 从形式上来看，DCT 是线性可逆变换。函数 F Rn ，R 是是实数集，或者等价为一个 n × -1 变换到实数 f0, + 12 f1,…, =0,1,2,…, n k -1 ， -1 f n N n 的方阵。离散余弦变换有四 3 （ ） : Rn → 3 ）把实数 x0, x1,…, =∑ π x cosé mæ è ëê -1 =0 n x f m N n k k ù ö ø ûú 2 DCT 图像压缩的 Matlab 实现： 基于 DCT 的图像压缩编码理论，得出图像压缩及解压过程如图 ： 图2 DCT 图像压缩及解压过程[5] 2 2 8×8 在 Matlab 图像处理中，可以直接调用 dct 来实现二维 DCT 及其反变换。在编码过程中，首先将输入图像颜色空间转 个交流系数 换后分解为 值）。接着对 DCT 系数进行量化，并将得到的量化系数进行编码和传送，这样就完成了图像的压缩。解码过程同样通过 DCT 系数 的解码、逆量化、IDCT ，最后将还原块组合成单一图像即完成图像解压。 大小的数据块，然后用正向二维 DCT 把每个块转化为 个 DCT 系数值（包括一个直流系数值与 和 idct 64 63 Matlab 调用函数见表 2 ： = b ( dct a , ) n 表2 DCT 及 IDCT 调用函数表 ( , n b idct = a ) 2.3 小波变换原理及 Matlab 实现 实现 DCT 变换 实现 IDCT 变换 小波变换原理： 小波变换是一种窗口大小固定但其形状可改变的时频局部化分析方法。连续小波变换存在信息冗余，所以只计算离散的位 4930 人工智能及识别技术 本栏目责任编辑：唐一东 

第9 卷第21 期 (2013 年07 月) ComputerKnowledgeandTechnology电脑知识与技术 移和尺度下的小波变换值可以有效的节约计算。小波变换将图像分为近似与细节（小尺度的瞬变）两部分。在本尺度内将细节储 存，对近似部分在下一尺度上进行分解，重复该过程即为小波变换 ，见图 。 [6] 3 小波变换的 Matlab 实现： 利用 Matlab 小波工具箱，编写函数 wavecomp( 参数设定。采用全局阀值处理方法，比较不同情况下压缩图像的质量。 3 图像变换结果分析 1) DFT 图像变换：设置不同的 Quotiety（量化系数）下的解压复原图像，见图 4 。 图3 小波变换图像压缩流程 , I thr ，该函数可使用函数 wavedec ) [7] 2 对图像 I 进行小波变换压缩，阀值由 thr 输入 原图像 30db =5 =37.6878 quotiety PSNR PSNR 图4 DFT 压缩图像 =10 =33.6847 quotiety quotiety PSNR =20 =17.3884 PSNR =10 quotiety 2) 由图像知 PSNR 在 以上的图像质量较高，人眼感受到的与原图像的差别较小。对于满足较好的 与较大的压缩率， 是最佳选择。 DCT 图像变换：下图 5 是用不同的量化表进行压缩图像所形成的结果。经过不同的压缩比可以很容易的比较出图像压缩 后的质量。 原图像 =1 文件14.0KB quotiety =2 quotiety 文件10.0KB =5 quotiety 文件6.25KB 图5 DCT 压缩图像 仿真结果说明当图像压缩比增大时，压缩效率减小，图像质量降低。但是，当压缩比较高时，这种块的独立处理带来了压缩效 率上的限制和方块效应问题，方块效应成为限制 DCT 编码质量的主要因素。 3) 小波变换图像变换，见图 ： 6 原图像 （a） 图6 小波变换压缩图像 （b） （c） 本栏目责任编辑：唐一东 人工智能及识别技术 4931 

ComputerKnowledgeandTechnology电脑知识与技术 第9 卷第21 期 (2013 年07 月) c b c 0 0 0 n 百分比：coef ）小波变换系数为 ）小波变换系数为 （ 压缩图像剩余能量百分比： （ 压缩图像剩余能量百分比： （ 压缩图像剩余能量百分比： 小波变换对图像采取了多分辨率的分解方式，和人眼的观察方式相一致。在编码的同时将量化失真随机地分布在全图中，实 ）小波变换系数为 百分比：coef 百分比：coef n n Re Re Re =30.4234 =99.9903 =38.6573 =99.9669 =43.8645 =99.9543 现了高压缩比低失真度的效果。从上图也可看出经过小波变换压缩的图像较难用人眼识别图像的变化。 4 结束语 , 基于小波变换和层式 图像变换是图像压缩的一项重要技术 如何准确、快速的进行图像压缩一直是国内外研究的热点。该文简述了 DFT 、DCT 以 及小波变换的原理，并通过 Matlab 模拟 DFT 、DCT 以及小波变换过程。通过对比分析经过三种不同的压缩方式所压缩的图片效 果，得出小波变换明显优于 DCT 变换和 DFT 变换。 参考文献： [1] [2] [3] [4] Wikipedia,DiscreteFouriertransform[EB\OL].http://en.wikipedia.org/wiki/Discrete_Fourier_transform. [5] [6] [7] ,2007. ,2008,107(7):43-46. ,2013,1(22):42-46. ,2009,28(5). 变换的图像压缩技术研究 基于小波包的图像压缩处理 [D]. ,2003:56-57. [J] . ,2006,1(21):51-54. 数字图像处理 基于 的数字图像压缩编码的研究与实现 [J]. [J]. Matlab 西安：西安电子科技大学出版社 和小波变换的图像压缩及 贾萍 何东健 贺勤 DCT , . . 天津：天津师范大学 [M]. DCT Matlab 大众科技 DCT 郭力争 张亚东 田勇 实现 . , , , , , . , , . . 河南城建学院学报 光电技术应用 实现 [J]. 电脑知识与技术 王永皎 刘晶 张波 系晓梁 周文娟 基于 周晓东 等 杨晓 , 等 基于小波包的图像压缩及 （上接第4920页） Rabin , , , TB PB , EB . , , , , , . . , , 基于 级 甚至 [J]. [J]. 程学旗 URL 级上升到 指纹方法的 计算机工程 已从前几年的 Rabin , . 企业对存储的需求越来越大 高速网络环境下的垃圾邮件快速检测技术 刘杰 梁正友 杨天奇 辛毅 付印金 ogy, Harvard University. 张林才 周晔 方滨兴 肖侬 以 随着数据信息的爆炸性增长 , 2006(04): 139-141. , 2008(S2): 185-186+203. 指纹作为数据块划分依据的重复数据检测方法适合应用于更新频繁的数据集，已被国内外很多存储系统所采用。近 年来 级。由于网络共享手段 的日益普及，人们交流数据的机会大大增加，以网络硬盘为代表的网络存储系统中充斥着大量的重复数据。重复数据检测和删除 技术的应用必将能带来巨大的效益。 参考文献: [1] Rabin Michael O. Fingerprint by random polynomials. 1981, Technical Report TR-15-81, Center for Research in Computing Technol⁃ [2] [3] [4] [5] [6] [7] Athicha M, Chen Ben-jie, Mazieres David. A low-bandwidth network file system[C]. ACM SIGOPS Operating Systems Review. 2001: [8] Cox Lan-don P, Murray Christopher D, et al. Pastiche: Making backup cheap and easy[J]. ACM SIGOPS Operating Systems Review, [9] You Lawrence L, Pollack Kristal T, Long Darrell De. Deep Store: An Archival Storage System Architecture[C]. Proceedings of the [10] [11] [12] [13] ACM. 2002. 36(SI): 285-298. 21st International Conference on Data Engineering. 2005: IEEE Computer Society. , 2011(S1): 100-104. , 2011(11): 3586-3589+3617. , 2013(01): 5-7+14. 王树鹏 杨频 数据备份系统中数据去重技术研究 一种基于重复数据删除的 计算机工程 信息采集方法 的网络恶意代码检测技术研究 一种增量式并行 云晓春 基于 刘芳 , 2006(20): 97-99. [J]. , 2008(10): 1029-1034. 基于重复数据删除的多用户文件备份系统 [J]. , 2012. 一种并行层次化的重复数据删除技术 , 2012(01): 12-20. 贾志凯 马建庭 谭玉娟 李向前 重复数据删除关键技术研究进展 计算机研究与发展 计算机研究与发展 计算机工程与设计 数据库备份系统 电脑知识与技术 [J]. [J]. Web P2P 华中科技大学 Oracle 计算机应用 高技术通讯 去重算法 陈光达 [D]. [J]. [J]. 武汉 , , . . 等 . , 等 . , . : 4932 人工智能及识别技术 本栏目责任编辑：唐一东