logo资料库

基于改进粒子群算法的三维装箱优化研究.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.64M 资料格式：pdf 举报 版权申诉
第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
资料共11页，剩余部分请下载后查看
    中国科技论文在线 http://www.paper.edu.cn 基于改进粒子群算法的三维装箱优化研究 杨志强，牛占文，党培** （天津大学管理与经济学部） 5 10 摘要：本文提出一种适用于求解三维装箱问题的改进粒子群优化算法。该算法在简化粒子群 优化算法的基础上，引入小生境技术实现初始种群的分组，各子群单独进化以增强种群的多 样性，提升算法的局部搜索能力；在进化过程中周期性地取出各子群最优粒子组成新种群， 应用混合蛙跳算法实现各子群间信息的交流，提升算法的全局寻优能力。对比结果表明改进 算法显著提高求解效率，有效提升空间利用率，验证改进算法的有效性与优越性，并给出装 载方案三维显示。 关键词：三维装箱；粒子群算法；小生境；混合蛙跳 中图分类号：U695.2+2 15 Research of an improved particle swarm algorithm in three-dimensional bin packing problem Yang Zhiqiang, Niu Zhanwen, Dang Pei (College of Management and Economics，Tianjin University，Tianjin,300072) Abstract: This paper presents an improved particle swarm algorithm for the three-dimensional bin packing problem. In this algorithm, the niche technology is introduced to the simple particle swarm optimization while the initial population is divided into multiple sub-swarms and each sub-swarm can be evolved independently to enhance the diversity of the population and improve the local search capability. In the process of evolution, the best particle in the sub-swarms are reformed into a new group periodically and the new group can be evolved by shuffled frog leaping algorithm to promote the communication of sub swarms and the global search ability further .Compared with the original algorithm, the improved algorithm has much higher computing efficiency. Case simulation is done to verResearch of an improved particle swarm algorithm in three-dimensional bin packing problemify the efficiency and superiority of the improved particle swarm algorithm, and the 3-D display of the results is given. Key words: three-dimensional bin packing; particle swarm algorithm; niche technology; shuffled frog leaping algorithm 20 25 30 0 引言 三维装箱问题（Three-dimensional bin packing problem,3-D BPP）广泛存在于物流领域中， 35 随着物流标准化的推行，其重要性日益凸显。优良的装载方案可以节约单位货物的运输成本， 提高装载效率，提升企业的盈利能力。该问题是典型的组合优化问题，随着装箱规模的增加 会发生“组合爆炸”的现象，属于最高计算复杂性的 NP（Non-deterministic Ploynomial）完全 问题。因此，研究三维装箱问题具有积极的现实意义和重要的理论价值。 三维装箱问题研究范围较广，结合实际应用需要考虑的情况也有很大不同。按集装箱数 40 量可分为单箱问题、多箱问题；按照货物的异构强弱程度又可分为同构货物、弱异构货物和 强 构 货 物 [1] 。 本 文 研 究 单 箱 弱 异 构 货 物 装 箱 问 题 （ Single large object placement problem,SLOPP），即给定一个箱体和若干较少类型的待装载货物，其中箱体与货物均为长 方体且大小给定，要求确定一个可行的装载方案使得在满足给定约束条件下最大化箱体的空 作者简介：杨志强（1992-），男，硕士研究生，主要研究方向：工业工程与管理，智能算法 通信联系人：牛占文（1966-），男，内蒙古自治区人，教授，博导，主要研究方向：工业工程与管理. E-mail: zw.niu@163.com - 1 -
    中国科技论文在线 http://www.paper.edu.cn 间利用率。可行的装载方案必须满足：（1）装入的货物必须完全包含在箱体内；（2）任意 45 两个货物互不相嵌。此外在实际情况中，还需要考虑一些具体的约束，例如方向性约束和稳 定性约束。（1）方向性约束。限制货物的放置方向，例如现实生活中由于封装方式不同， 货物的封口面一般向上（2）稳定性约束。装入货物不能悬空，其底面必须获得部分或完全 50 55 支撑，保证货物在装载或运输过程的稳定性。 因“组合爆炸”现象，直接利用数学优化算法求解三维装箱问题的规模有限，国内外研究 主要以启发式算法和人工智能算法为主。在启发式算法方面，George[2]等人提出了一种砌墙 算法，首次给出了层的概念；Bischoff[3]等人拓展了层的概念提出了基于完全层的启发式算 法，并将二维装箱问题求解方法应用到三维空间；与层的概念不同，Elay[4]设计了基于同类 块（同货物同方向组合的货块）的树搜索算法，该算法在利用率和稳定性方面都取得了不错 的结果；那日萨[5]等人采用货物块的概念，根据可用空间应用启发式算法确定最佳货块。在 人工智能算法方面，Gehring[6]、Bortfeldt[7]、Mark[8]等分别将遗传算法、禁忌算法与模拟退 火算法应用到了三维装箱问题上。为弥补算法缺陷也涌现了许多改进算法：游伟[9]等人提出 了一种偏随机密钥混合遗传算法；Kang[10]等人提出了一种基于剩余空间最小装载策略的混 合遗传算法；张德富[11]等人将启发式算法与模拟退火算法进行结合，提出了一种混合模拟 退火算法； 60 粒子群优化算法（Particle swarm optimization, PSO）是一种典型的群智能算法，与遗传 算法、模拟退火算法等进化算法相比，具有结构简单、容易实现、收敛速度快和鲁棒性强等 优势，广泛应用于函数优化、模式识别、模糊系统控制、神经网络训练以及其他工程领域中 [12]。目前已有部分研究将该算法应用于二维装箱问题，Zhao[13]等人设计了一种离散粒子群 算法求解二维排样问题；黄岚[14]等人提出一种遗传-离散粒子群优化算法求解矩形优化排样 问题，并验证了改进算法的高效性与鲁棒性。三维装箱问题由于其复杂性和难度较前者大， 目前相关的研究较少，Domingo[15]等人应用粒子群优化算法求解单容器装箱问题，在弱异构 类装箱问题上取得了较好的结果；孟非[12]等人在简化粒子群算法中引入混合蛙跳算法的分 65 组思想，取得了较高的容积利用率。 在文献[12,15]研究的基础上，提出一个改进粒子群优化算法。该算法与文献[12]的差异在于， 70 文献[12]将粒子群按照适应度值大小进行分组，结合混合蛙跳算法进行更新迭代；而本文采用 小生境技术+混合蛙跳算法的改进策略，将初始种群按照欧式几何距离（装箱序列差异）分 成多个子群（小生境），各子群单独进化，周期性地取出各子群最优粒子组成新种群应用混 合蛙跳算法进行更新，进一步提升种群多样性与全局寻优能力。在装载策略上，与三空间法 不同，针对装箱工人一般将同类货物堆叠形成同类块的装载逻辑，本文采用同类块的思想[4]， 75 运用二维排样算法实现装箱方案的装载，简化装载步骤。 1 目标函数与装载策略 1.1 目标函数 设箱体的长、宽、高分别为 L、W、H，待装载货物的集合为 ，货物 的长、宽、高分别为 、 、 ， 表示货物 装入集装箱中； 表示货物 80 未装入集装箱中，需要达到的要求为满足给定约束条件下的最大体积装载率，以提高集装箱 - 2 - 12={,,,}nCCCCiCiliwih1iaiC0iaiC
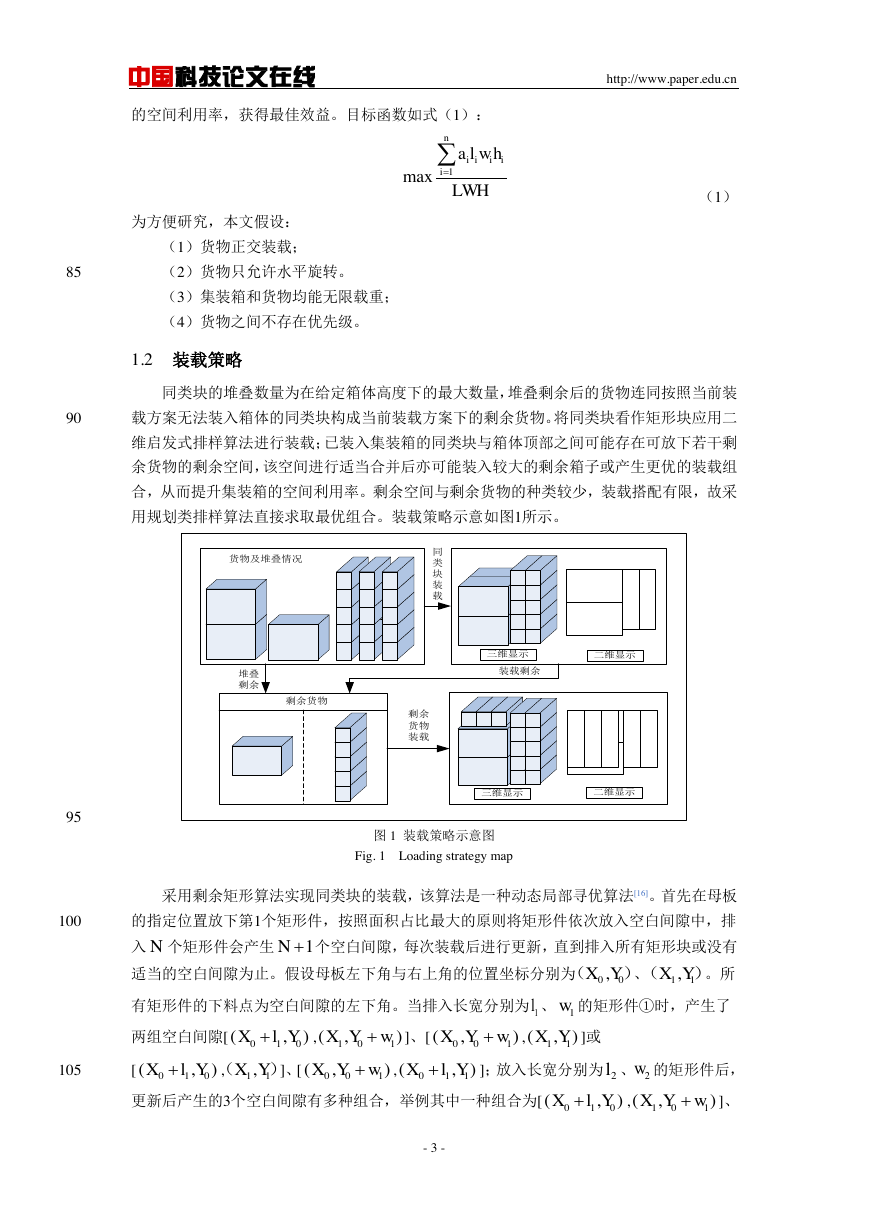
    中国科技论文在线 http://www.paper.edu.cn 的空间利用率，获得最佳效益。目标函数如式（1）： （1） 为方便研究，本文假设： （1）货物正交装载； 85 （2）货物只允许水平旋转。 （3）集装箱和货物均能无限载重； （4）货物之间不存在优先级。 1.2 装载策略 同类块的堆叠数量为在给定箱体高度下的最大数量，堆叠剩余后的货物连同按照当前装 90 载方案无法装入箱体的同类块构成当前装载方案下的剩余货物。将同类块看作矩形块应用二 维启发式排样算法进行装载；已装入集装箱的同类块与箱体顶部之间可能存在可放下若干剩 余货物的剩余空间，该空间进行适当合并后亦可能装入较大的剩余箱子或产生更优的装载组 合，从而提升集装箱的空间利用率。剩余空间与剩余货物的种类较少，装载搭配有限，故采 用规划类排样算法直接求取最优组合。装载策略示意如图1所示。 95 图 1 装载策略示意图 Fig. 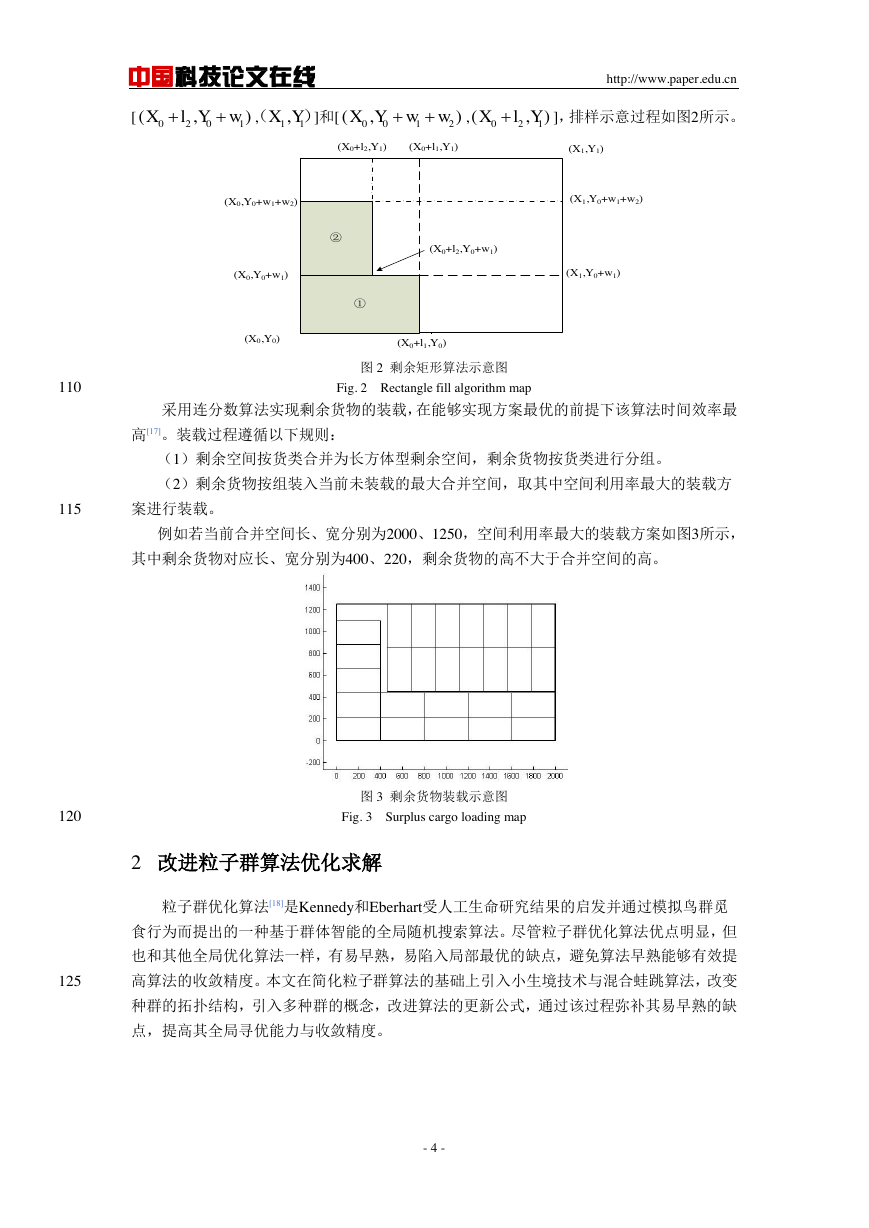1 Loading strategy map 采用剩余矩形算法实现同类块的装载，该算法是一种动态局部寻优算法[16]。首先在母板 100 的指定位置放下第1个矩形件，按照面积占比最大的原则将矩形件依次放入空白间隙中，排 入 个矩形件会产生 个空白间隙，每次装载后进行更新，直到排入所有矩形块或没有 适当的空白间隙为止。假设母板左下角与右上角的位置坐标分别为 、 。所 有矩形件的下料点为空白间隙的左下角。当排入长宽分别为 、 的矩形件①时，产生了 两组空白间隙[ , 105 [ , ]、[ ]、[ , , ]或 ]；放入长宽分别为 、 的矩形件后， 更新后产生的3个空白间隙有多种组合，举例其中一种组合为[ , ]、 - 3 - 1maxniiiiialwhLWH同类块装载二维显示三维显示11三维显示二维显示剩余货物装载堆叠剩余装载剩余货物及堆叠情况剩余货物N1N00,XY（）11,XY（）1l1w010(,)XlY101(,)XYw001(,)XYw11(,)XY010(,)XlY11,XY（）001(,)XYw011(,)XlY2l2w010(,)XlY101(,)XYw
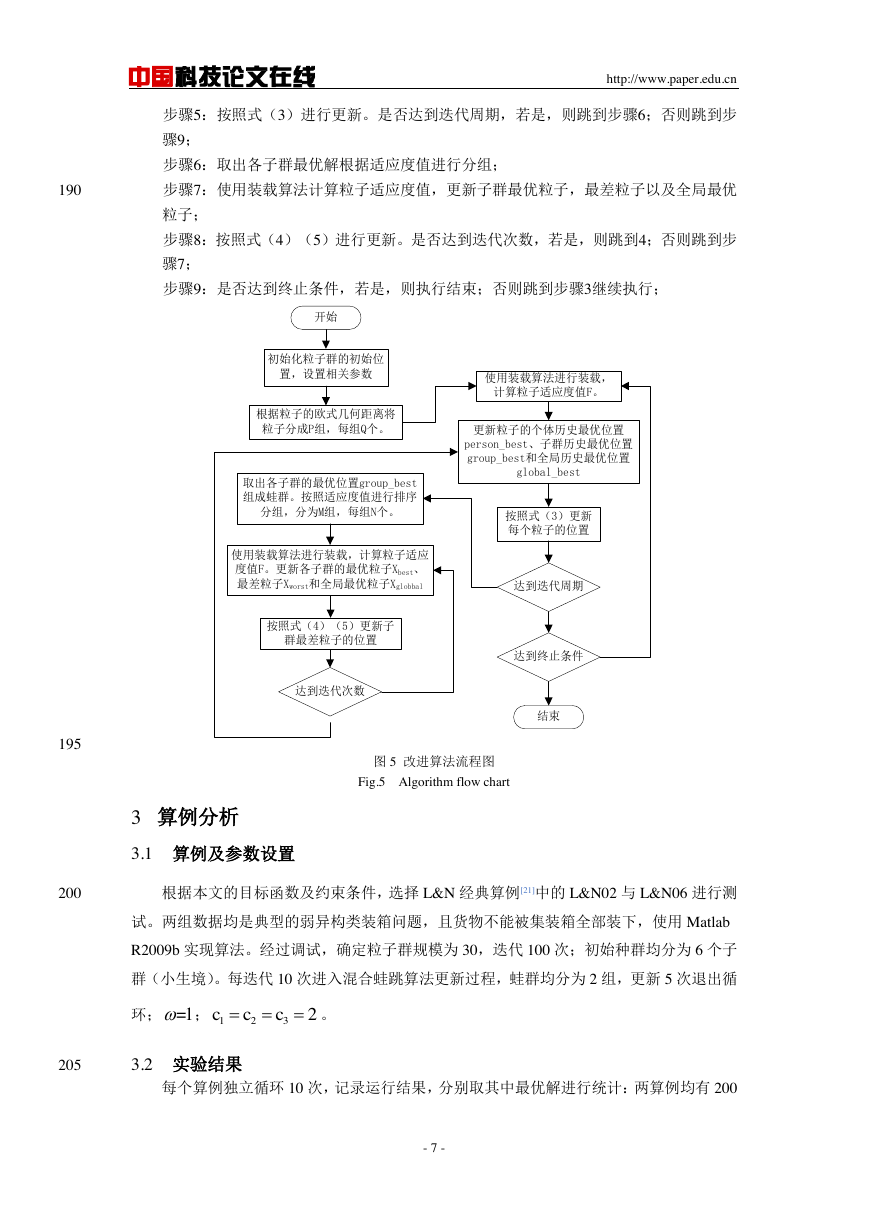
    中国科技论文在线 http://www.paper.edu.cn [ , ]和[ , ]，排样示意过程如图2所示。 110 图 2 剩余矩形算法示意图 Fig. 2 Rectangle fill algorithm map 采用连分数算法实现剩余货物的装载，在能够实现方案最优的前提下该算法时间效率最 高[17]。装载过程遵循以下规则： （1）剩余空间按货类合并为长方体型剩余空间，剩余货物按货类进行分组。 （2）剩余货物按组装入当前未装载的最大合并空间，取其中空间利用率最大的装载方 115 案进行装载。 例如若当前合并空间长、宽分别为2000、1250，空间利用率最大的装载方案如图3所示， 其中剩余货物对应长、宽分别为400、220，剩余货物的高不大于合并空间的高。 120 图 3 剩余货物装载示意图 Fig. 3 Surplus cargo loading map 2 改进粒子群算法优化求解 粒子群优化算法[18]是Kennedy和Eberhart受人工生命研究结果的启发并通过模拟鸟群觅 食行为而提出的一种基于群体智能的全局随机搜索算法。尽管粒子群优化算法优点明显，但 也和其他全局优化算法一样，有易早熟，易陷入局部最优的缺点，避免算法早熟能够有效提 125 高算法的收敛精度。本文在简化粒子群算法的基础上引入小生境技术与混合蛙跳算法，改变 种群的拓扑结构，引入多种群的概念，改进算法的更新公式，通过该过程弥补其易早熟的缺 点，提高其全局寻优能力与收敛精度。 - 4 - 0201(,)XlYw11,XY（）0012(,)XYww021(,)XlY①②(X0,Y0)(X1,Y1)(X0+l1,Y0)(X1,Y0+w1)(X1,Y0+w1+w2)(X0+l2,Y1)(X0+l1,Y1)(X0,Y0+w1)(X0,Y0+w1+w2)(X0+l2,Y0+w1)
    中国科技论文在线 2.1 简化粒子群算法 http://www.paper.edu.cn 经典粒子群算法中粒子包含位置与速度两个基本属性，粒子的更新通过改变粒子的速度 130 间接影响粒子位置来实现。文献[19]通过分析经典粒子群算法的运行机制，提出进化过程与粒 子速度无关的定理，剔除了经典粒子群算法中的速度项，仅由粒子位置控制进化过程，避免 了由粒子速度项引起的粒子发散而导致后期收敛变慢和精度低的问题。简化后的更新公式如 式（2）： （2） 135 式（2）中 表示收缩因子； 代表当前的演化代数， 代表当前演化代数的下一代； 、 分别表示粒子在第 、 代的位置； 、 分别表 示个体的历史最优位置和群体的历史最优位置； 、 分别表示个体学习因子和全局学习 因子； 、 均表示 0 到 1 之间的随机数。 2.2 编码方式及基本操作 140 2.2.1 编码方式 （1）粒子位置，一个装载序列 就代表了一个粒子的位置， 即装箱方案的一个解。其中 代表货块的类; 表示旋转因子，其取值为 1 或-1， 表 示货块正常装载， 表示货块水平旋转 90°装载。 （2）置换子，设粒子 k 的位置为 ，则置换子 代表交换 中序号为 和 145 的货块位置，并继承置换子中的旋转因子。即 ，其中 为粒子 k 经过置换子 的操作后所达到的新位置。若干置换子按照顺序排列构成置换序列； 粒子间距用置换序列进行表示。 2.2.2 基本操作 位置 间距：将置换序列按顺序依次作用在粒子位置上，生成新的粒子位置； 150 （2）位置 位置：计算两个粒子的位置间距，得到粒子间距（置换序列）； （3）间距 间距：两个粒子间距（置换序列）按照顺序组合成一个新的置换序列； （4）实数 间距：实数与置换序列中置换子的数量相乘，向前取整得到整数 ，取出 前 个置换子构成新的置换序列。 举例某粒子的更新过程如图 4 所示。 - 5 - (1)()11()22()(_)(_)ttttXwxcrpersonbestXcrglobalbestXt1t()tX(1)tXt1t_personbest_globalbest1c2c1r2r1122()nnXrNrNrN，，…，iNir1ir1irkX(,)ikjkrirjkXkikj'(,)kkikjkXXrirj'kX(,)ikjkrirjZZ
    中国科技论文在线 http://www.paper.edu.cn 155 图 4 粒子更新示意图 Fig.4 Update of a particle 2.3 改进粒子群优化算法 小生境技术（Niche Technology,NT）起源于遗传算法，该方法基于群体的随机优化算法 160 形成物种，利用其保持种群多样性的特点弥补粒子群算法易陷入局部最优的缺陷，同时提升 了种群的局部搜索能力[20]。应用过程为：计算每个粒子的欧式几何距离（装箱序列差异）， 将粒子按从小到大的顺序依次取出，将初始种群均分为 个子群，各子群单独进化。因此需 要增加新变量：子群的历史最优位置 ，更新公式变化如式（3）： 165 （3） 式（3）中 、 表示子群学习因子、全局学习因子； 表示0到1之间的随机数；其余 符号含义如式（2）。 为了实现各子群之间的信息交流，提升各子群最优解的质量，采用混合蛙跳算法 （Shuffled Frog Leaping Algorithm,SFLA）实现优化过程。该算法是一种群体进化算法，先 170 将种群划分为若干个子群进行局部搜索，再全局混合以达到全局交流的目的，有效提升种群 的全局寻优能力[12]。应用过程为：达到迭代周期后，取出各子群最优解组成蛙群，按照适应 度值依跨度均分为M个子群，在每个子群中，记录下当次迭代适应度最好的个体 和适 应度最差的个体 ，并计算两者之间的间距 ，同时记录整个蛙群的最优个体 。 在每次迭代时，对子群中适应度最差的个体 进行更新，如下所示： 175 （4） 式（4）中 表示0到1之间的随机数；式（5）中 、 分别表示子群最差 个体的新解与旧解； 、 分别表示间距的最小值与最大值。更新过后，若有改进， 则用新解替代旧解；若没有改进，则将 替换 进行更新；若仍无改进，则随机产 （5） 180 生一个解替代旧解。 2.4 算法流程 改进粒子群优化算法具体流程如图5所示： 步骤1：初始化粒子群的初始位置，设置相关参数； 步骤2：根据粒子的欧式几何距离（序列差异程度）将粒子群分组； 185 步骤3：使用装载算法计算粒子适应度值； 步骤4：更新粒子的个体历史最优位置、子群历史最优位置以及全局历史最优位置； - 6 - -84-71-2536置换子（-3,4）-8-361-2547原粒子位置置换子（6,7）新粒子位置P_groupbest(1)()11()22()33()(_)(_)(_)tttttXwxcrpersonbestXcrgroupbestXcrglobalbestX2c3c3rbestXworstXjdglobalXworstX()jbestworstdrXX,,minmax()worstnewworstoldjjXXddddr,worstnewX,worstoldXmindmaxdglobalXbestX
    中国科技论文在线 http://www.paper.edu.cn 步骤5：按照式（3）进行更新。是否达到迭代周期，若是，则跳到步骤6；否则跳到步 骤9； 步骤6：取出各子群最优解根据适应度值进行分组； 190 步骤7：使用装载算法计算粒子适应度值，更新子群最优粒子，最差粒子以及全局最优 粒子； 步骤8：按照式（4）（5）进行更新。是否达到迭代次数，若是，则跳到4；否则跳到步 骤7； 步骤9：是否达到终止条件，若是，则执行结束；否则跳到步骤3继续执行； 195 图 5 改进算法流程图 Fig.5 Algorithm flow chart 3 算例分析 3.1 算例及参数设置 200 根据本文的目标函数及约束条件，选择 L&N 经典算例[21]中的 L&N02 与 L&N06 进行测 试。两组数据均是典型的弱异构类装箱问题，且货物不能被集装箱全部装下，使用 Matlab R2009b 实现算法。经过调试，确定粒子群规模为 30，迭代 100 次；初始种群均分为 6 个子 群（小生境）。每迭代 10 次进入混合蛙跳算法更新过程，蛙群均分为 2 组，更新 5 次退出循 环； ； 。 205 3.2 实验结果 每个算例独立循环 10 次，记录运行结果，分别取其中最优解进行统计：两算例均有 200 - 7 - 开始初始化粒子群的初始位置，设置相关参数根据粒子的欧式几何距离将粒子分成P组，每组Q个。使用装载算法进行装载，计算粒子适应度值F。按照式（3）更新每个粒子的位置达到终止条件结束达到迭代周期取出各子群的最优位置group_best组成蛙群。按照适应度值进行排序分组，分为M组，每组N个。使用装载算法进行装载，计算粒子适应度值F。更新各子群的最优粒子Xbest、最差粒子Xworst和全局最优粒子Xglobbal按照式（4）（5）更新子群最差粒子的位置达到迭代次数更新粒子的个体历史最优位置person_best、子群历史最优位置group_best和全局历史最优位置global_best=11232ccc
    中国科技论文在线 http://www.paper.edu.cn 个货物，其中 L&N02 装入 172 个货物，空间利用率为 91.93%；L&N06 装入 139 个货物， 空间利用率为 92.25%。具体装载信息如表 1 所示。 表 1 实验结果 210 Tab. 1 Experimental results 装载顺序 L&N02 装入数量 是否旋转 装载顺序 L&N06 装入数量 是否旋转 8 4 7 1 2 5 3 6 16 18 25 28 36 15 34 0 是 否 是 否 是 否 否 否 8 7 6 5 4 1 2 3 15 10 21 25 24 32 12 0 是 否 否 否 是 是 是 是 空间利用率 91.93% 空间利用率 92.25% 为了直观地显示装载方案，方便装载。分别给出 L&N02（图 6（a））与 L&N06（图 6 （b））的装载方案三维显示图。 215 220 （a）L&N02 装载效果图 （b）L&N06 装载效果图 图 6 装载方案效果图 Fig.6 Loading scheme map 举例给出 L&N02 的同类块、剩余货物的装载位置坐标，坐标对应点均为装载单位的前 左下角对应的点，如表 2、表 3 所示。其中表 2 表示同类块的装载位置坐标；表 3 表示剩余 货物的装载位置坐标。 表 2 L&N02 同类货块装载信息 Tab. 2 L&N02 Congeneric cargo block loading information 货块类及方向 X 轴坐标 Y 轴坐标 货块类及方向 X 轴坐标 Y 轴坐标 -8 -8 4 4 4 4 4 4 4 4 0 200 400 900 1400 0 500 1000 1500 0 1 1 1 1 1 -2 -2 -2 -2 -2 0 0 0 0 0 375 375 375 375 750 - 8 - 0 400 800 1200 1600 0 400 800 1200 1600 1500 1500 1650 1650 1650 1875 1875 2025 2025 2025
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料