数学建模实验报告.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：0.48M 资料格式：pdf 举报版权申诉

layliangbo-10503225-4744302542910320148.pdf-第1页.png

第1页 / 共27页

layliangbo-10503225-4744302542910320148.pdf-第2页.png

第2页 / 共27页

layliangbo-10503225-4744302542910320148.pdf-第3页.png

第3页 / 共27页

layliangbo-10503225-4744302542910320148.pdf-第4页.png

第4页 / 共27页

layliangbo-10503225-4744302542910320148.pdf-第5页.png

第5页 / 共27页

layliangbo-10503225-4744302542910320148.pdf-第6页.png

第6页 / 共27页

layliangbo-10503225-4744302542910320148.pdf-第7页.png

第7页 / 共27页

layliangbo-10503225-4744302542910320148.pdf-第8页.png

第8页 / 共27页

实验名称：微分方程

实验目的:

理学院数学系实验报告课程名称：实验学期：实验班级：学生学号：学生姓名：数学建模 2017-2018 第二学期软件工程 1606 班 20165087 黄蕾指导教师：李春梅刘玲陆小军理学院数学实验中心二〇一八年六月二十二日

东北大学数学实验中心实验报告规范（暂行）一、每个学生每个实验项目一份实验报告。二、实验报告内容一般包括以下几个内容： 1. 实验项目名称 2. 实验目的和要求 3. 实验原理 4. 实验内容及步骤 5. 实验数据记录和处理 6. 实验结果与分析（含以上 1、2、3、4、5、6 项，需经指导教师签字认可，附在实验报告后）注：各专业各课程的实验报告内容与格式可由指导教师根据实验具体情况做出要求。三、实验报告第一页按学院统一的实验报告格式书写，附页用 A4 纸书写，字迹工整，曲线要画在座标纸上，线路图要整齐、清楚（不得徒手画）。如打印也应采用统一的实验报告的版头（A4 纸）。四、每学期将拟存档的学生实验报告按课程、实验项目分类装订成册，即每个实验项目每门课程的所有实验报告装订成一本。装订线在左侧，第一页加订实验报告封皮。五、东北大学理学院数学实验报告模板范本，本实验报告双面打印（附后）。

理学院数学实验中心实验报告专业：软件工程姓名：黄蕾学号： 20165087 成绩：实验地点：数学实验中心指导教师签名：实验名称：Matlab 程序设计实验目的: [1] 熟悉 MATLAB 软件的用户环境； [2] 了解 MATLAB 软件的一般目的命令； [3] 掌握 MATLAB 数组操作与运算函数； [4] 掌握 MATLAB 软件的基本绘图命令； [5] 掌握 MATLAB 语言的几种循环、条件和开关选择结构。实验内容及步骤： 1．MATLAB 软件的数组操作及运算练习； 2．直接使用 MATLAB 软件进行作图练习； 3．用 MATLAB 语言编写命令 M-文件和函数 M-文件。实验要求： A  113 212 321           ， B  1 2 1      1 1  0 1    0   1  1. 已知矩阵求：（1）屏幕输出 A 与 B；（2）A 的转置 A′；（3）求 A+B 的值；（4）求 A-B 的值；（5）求 4A；（6）求 A×B；（7）求 A-1． 2. 有一函数 f(x,y)=x2+sinxy+2y，写一程序，输入自变量的值，输出函数值。

3. 用 plot，fplot 分别绘制函数 y=cos(tan(x))在部分自定义区域的图形。 4．建立一个 M 文件：求所有的“水仙花数”，所谓“水仙花数”是指一个三位数，其各位数字的立方和等于该数本身。例如：153 是一个水仙花数，因为 153=13+53+33。实验数据记录及处理：（1） A = B = A'= 3 2 1 1 2 1 3 1 1 A+B = 4 4 1 1 2 1 -1 0 2 1 2 2 0 1 2 3 -1 0 1 1 2 3 0 2

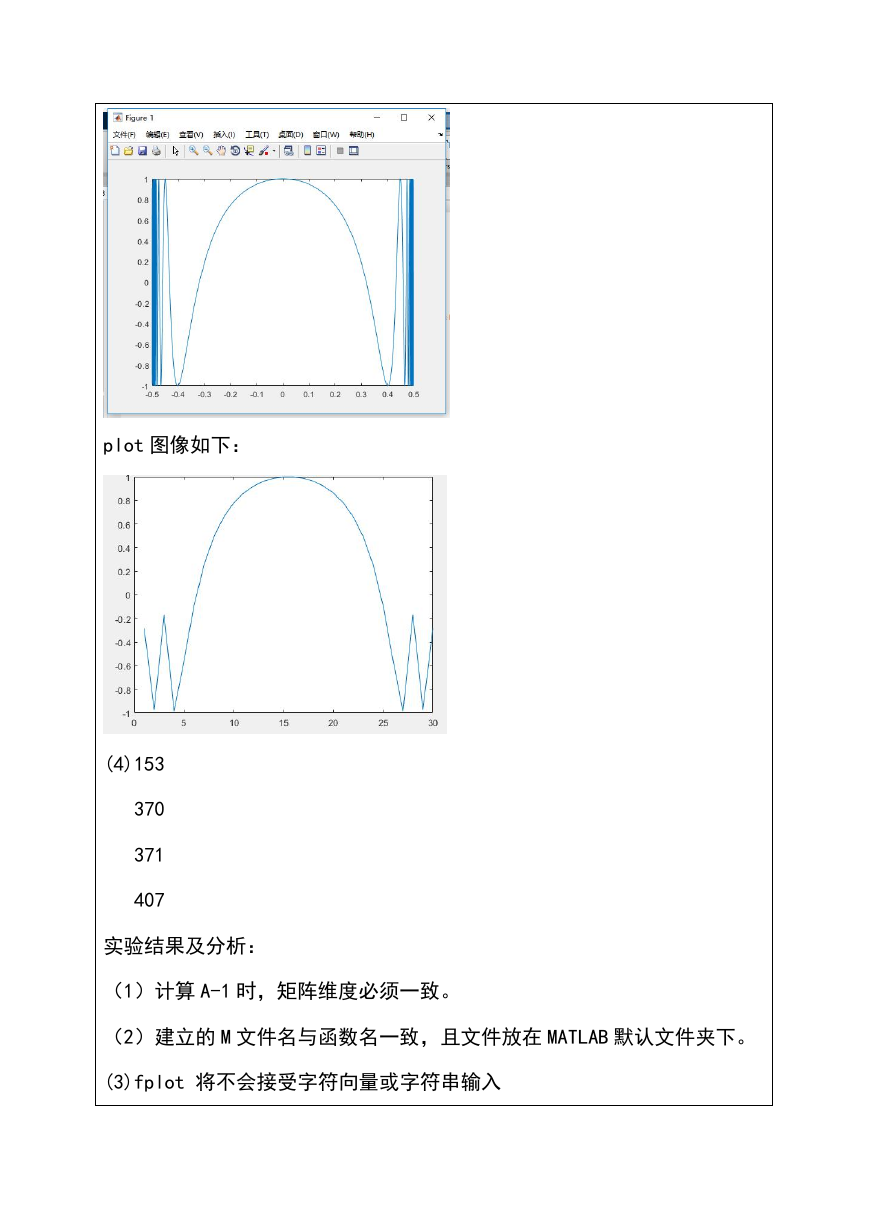
2 0 2 2 4 4 8 2 1 -1 4 2 2 2 4 8 12 -2 0 2 2 A-B = 2 0 0 4*A= 12 8 4 A*B = 6 6 8 1/A= 0.3333 1.0000 1.0000 0.5000 1.0000 0.5000 1.0000 0.5000 0.3333 （2）x=1,y=1,fun(x,y) f = 3.8415 ans =3.8415 (3)fplot 图像如下：

plot 图像如下： (4)153 370 371 407 实验结果及分析：（1）计算 A-1 时，矩阵维度必须一致。（2）建立的 M 文件名与函数名一致，且文件放在 MATLAB 默认文件夹下。 (3)fplot 将不会接受字符向量或字符串输入

理学院数学实验中心实验报告专业：软件工程姓名：黄蕾学号： 20165087 成绩：实验地点：数学实验中心指导教师签名：实验名称：线性规划实验目的: [1]掌握线性规划的建模技巧和求解方法； [2]熟悉 MATLAB 软件求解线性规划模型的基本命令； [3]通过范例学习，熟悉建立线性规划模型的基本要素和求解方法。 [4]认识面对现实生活中的最优化问题，怎样提出假设和建立优化模型 [5]学会使用 MATLAB 软件进行线性规划模型求解的基本命令。实验内容： 1．最优化问题的提出，提出不同的假设可以建立不同的最优化模型； 2．建立线性规划模型的基本要素和步骤； 3．使用 MATLAB 命令对线性规划模型进行计算。实验要求： 1.应用 matlab 求解以下线性规划模型 min .. ts 4 x  3 120   x 1 z 3 6 3 x x  1 2 x x   2 30 x  1 0 x   2 20 x  3 50 2. 某厂按合同规定须于当年每个季度末分别提供 10,15,25,20 台同一规格的柴油机。已知该厂各季度的生产能力及生产每台柴油机的成本如下表所

示，如果生产出的柴油机当季不交货，每台积压一个季度需储存、维护等费用 0.15 万元，试建立一个数学模型，要求在完成合同的情况下，使该厂全年生产（包括储存、维护）费用最小。成本（万元/ 季度生产能力（台）台）一二三四 25 35 30 10 10.8 11.1 11.0 11.3 实验数据记录及处理：（1）x = 30 50 40 fval = 490 （2）设该工厂每季度生产柴油机数量分别为 x1,x2,x3,x4. 则第一季度储存维护费用为：0.15*(x1-10); 第二季度储存维护费用为：0.15*（x1-10+x2-15）; 第三季度储存维护费用为：0.15*(x1-10+x2-15+x3-25); 即可以建立线性规划模型： Min z=x1*10.8+x2*11.1+x3*11.0+x4*11.3+0.15*[(x1-10)+(x1+x2-25)+ (x1+x2+x3-50)=11.25*x1+11.4*x2+11.15*x3+11.3*x4-12.75;

分享到：

赞收藏

资料库

数学建模实验报告.pdf

相关推荐

课程资源

热门标签

最新资料