vrp网络模型的数学建模描述.pdf-资料库

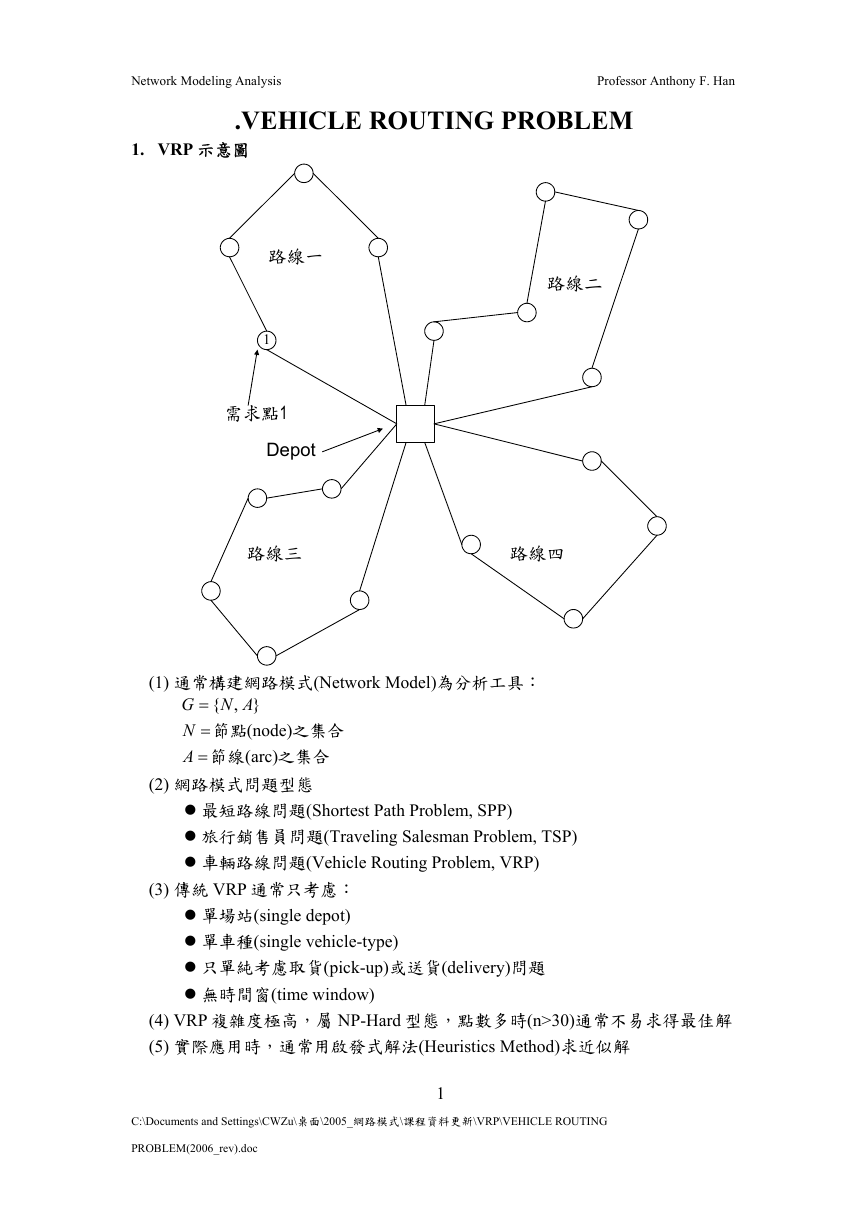
Network Modeling Analysis Professor Anthony F. Han .VEHICLE ROUTING PROBLEM 1. VRP 示意圖路線二路線一 1 需求點1 Depot 路線三路線四 (1) 通常構建網路模式(Network Model)為分析工具： G N A AN } ,{ = = 節點 = 節線 (node) (arc) 之集合之集合 (2) 網路模式問題型態最短路線問題(Shortest Path Problem, SPP) 旅行銷售員問題(Traveling Salesman Problem, TSP) 車輛路線問題(Vehicle Routing Problem, VRP) (3) 傳統 VRP 通常只考慮：單場站(single depot) 單車種(single vehicle-type) 只單純考慮取貨(pick-up)或送貨(delivery)問題無時間窗(time window) (4) VRP 複雜度極高，屬 NP-Hard 型態，點數多時(n>30)通常不易求得最佳解 (5) 實際應用時，通常用啟發式解法(Heuristics Method)求近似解 1 C:\Documents and Settings\CWZu\桌面\2005_網路模式\課程資料更新\VRP\VEHICLE ROUTING PROBLEM(2006_rev).doc

Network Modeling Analysis Professor Anthony F. Han 2. VRP Formulation 2.1 Golden’s Formulation (Golden 1977) [CAOR pp.96.97] Minimize Subject to N N NV ∑∑∑ j 1 = v = 1 i = 1 C ij x v ij + ⎛ ⎜ ⎝ ∑∑ f v v j x v 1 j ⎞ ⎟ ⎠ x v ij = 1 x v ij = 1 j ( = 2 ,..., N ) i ( = 2 ,..., N ) ∑∑ ∑∑ v v i j i i n ∑ 2 j = n ∑ i = 2 i j - =1 x v ip ∑∑ =1 Loading Capacity ∑∑ d x ( i x v pj = 0 v ij ) ≤ K v j path time constraint + ∑ ∑ x v i v ij t j p ( = ,..., 1 N v ; = ,..., 1 NV ) v ( = ,..., 1 NV ) t x v ij v ij ≤ T v ( v = 1 ,..., NV ) ∑∑ i j x v 1 j ≤ 1 x v i 1 ≤ 1 ( v = 1 ,..., NV ) ( v = ,..., 1 NV ) Subtour breaking } { 1 or 0 = X = x x ij v ij ∈ S ⎛ ⎜ ⎝ x ij = x v ij ∑ v ⎞ ⎟ ⎠ for all v, i and j 2.2 VRP Time-Window Constraints a ≤ a j i.e. (arrival time at j) ≤ a j j [ ∈ a aj , ] (time window) j v = 1 if xij a if x v ij = x ij = a i + t v i + v ij t j =∑ 0 a j = 0 Zero time 表示未曾到達 v nonlinear! a a + = x t i j v i v ij ( ) + ( 1 + − ( 1 − − where T is a large number and a ∑∑ v i ( t a + ( t a t ) ) a a t t + + ≤ ≥ + v ij v ij v i v i j i j i v ij ) x T v ij ) x T v ij a ≤ ≤ j j linear a j 2 C:\Documents and Settings\CWZu\桌面\2005_網路模式\課程資料更新\VRP\VEHICLE ROUTING PROBLEM(2006_rev).doc

Network Modeling Analysis Professor Anthony F. Han 3. VRP Heuristic Methods 求解策略(Solution Strategy)：兩階段 (1) 起始解產生 a. 節省法(Saving)或插入法(Insertion) b. Cluster First Route Second, e.g. Sweep Method c. Route First Cluster Second d. MP Approach, e.g. Generalized Assignment (2) 改進階段 a. 路線內(TSP)交換改善﹐如 2-opt, 3-opt b. 路線間交換改善在 PC 上節省法﹐掃描法﹐2-opt 均易執行平行(Parallel)節省法：較節省路程循序(Sequential)節省法：較節省車輛 4. Clark-and-Wright Savings Algorithm (1964) Symmetric distance (can be relaxed) id j saving ) ,( = (即單車連結 j i , 兩點比兩車分別服務此兩點所節省的距離) j iS ) ,( id )1 ,( j ) ,1( − + d i j Depot Procedure: (1) Calculate ( , ) (2) Make a “saving list” (由大至小) S i j (3) Include ( , ) i S i ( , ) in one route, if j for every node pair ( , ) j i Start from the largest j in the list a. both i and j not covered (new route) b. only one of i and j is covered and is external (add to old route) c. both are covered and external (combine two routes) (4) Continue to the next S i ( , ) j on the list until the list is exhausted, or all nodes are covered. If there are points left uncovered, they are covered each by a single route. 3 C:\Documents and Settings\CWZu\桌面\2005_網路模式\課程資料更新\VRP\VEHICLE ROUTING PROBLEM(2006_rev).doc

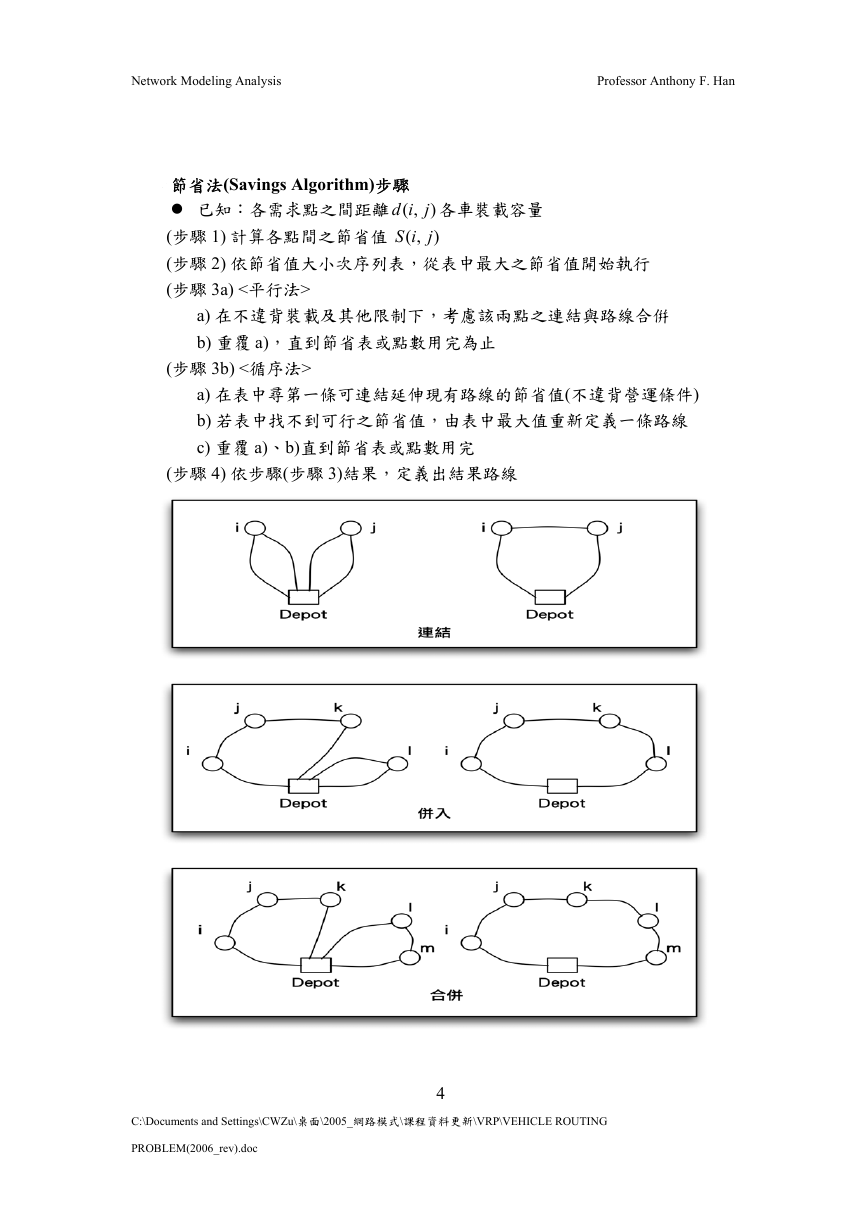
Network Modeling Analysis Professor Anthony F. Han 節省法(Savings Algorithm)步驟已知：各需求點之間距離 j id ) ,( 各車裝載容量 j S i (步驟 1) 計算各點間之節省值 ( , ) (步驟 2) 依節省值大小次序列表，從表中最大之節省值開始執行 (步驟 3a) <平行法> a) 在不違背裝載及其他限制下，考慮該兩點之連結與路線合倂 b) 重覆 a)，直到節省表或點數用完為止 (步驟 3b) <循序法> a) 在表中尋第一條可連結延伸現有路線的節省值(不違背營運條件) b) 若表中找不到可行之節省值，由表中最大值重新定義一條路線 c) 重覆 a)、b)直到節省表或點數用完 (步驟 4) 依步驟(步驟 3)結果，定義出結果路線 4 C:\Documents and Settings\CWZu\桌面\2005_網路模式\課程資料更新\VRP\VEHICLE ROUTING PROBLEM(2006_rev).doc

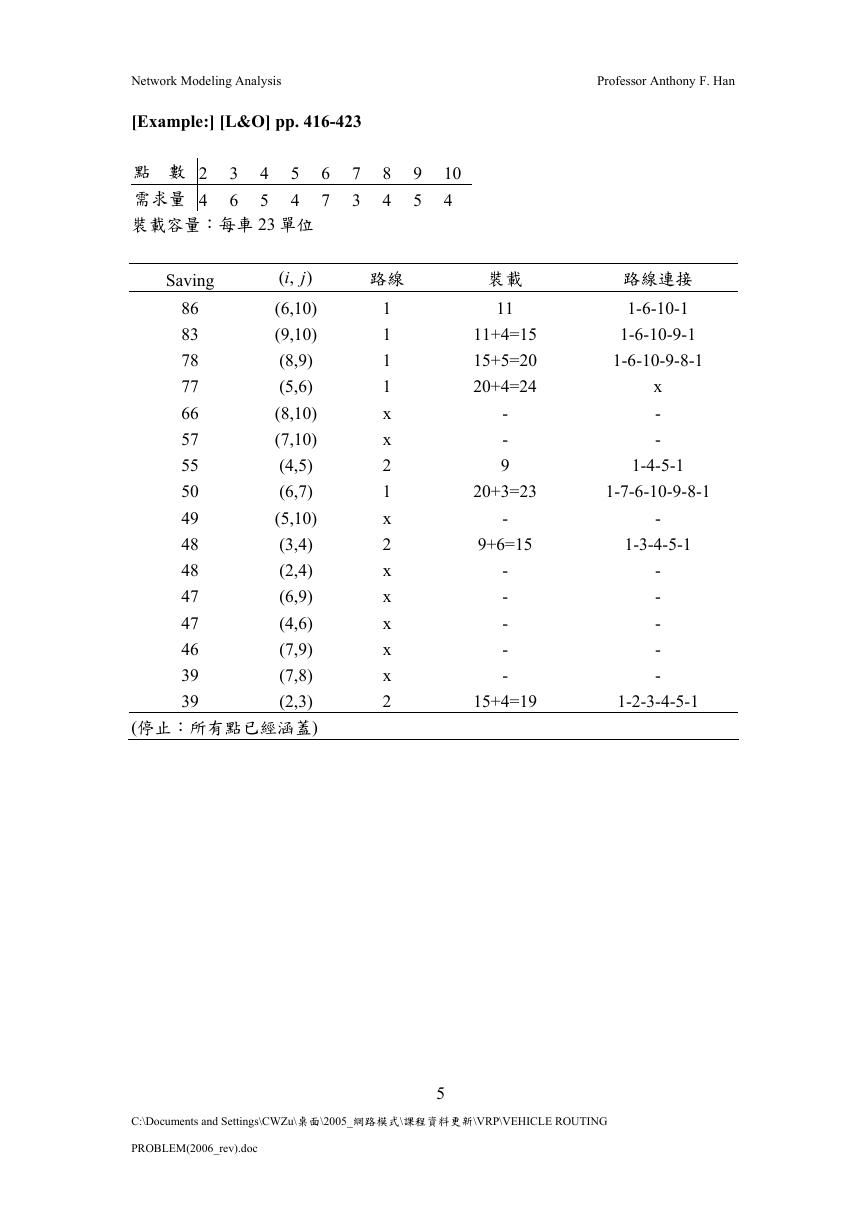
Network Modeling Analysis Professor Anthony F. Han [Example:] [L&O] pp. 416-423 點數 2 3 4 5 6 7 8 9 10 需求量 4 6 5 4 7 3 4 5 4 裝載容量：每車 23 單位路線 1 1 1 1 x x 2 1 x 2 x x x x x 2 裝載 11 11+4=15 15+5=20 20+4=24 - - 9 20+3=23 - 9+6=15 - - - - - 路線連接 1-6-10-1 1-6-10-9-1 1-6-10-9-8-1 x - - 1-4-5-1 1-7-6-10-9-8-1 - 1-3-4-5-1 - - - - - 15+4=19 1-2-3-4-5-1 Saving 86 83 78 77 66 57 55 50 49 48 48 47 47 46 39 39 i j ( , ) (6,10) (9,10) (8,9) (5,6) (8,10) (7,10) (4,5) (6,7) (5,10) (3,4) (2,4) (6,9) (4,6) (7,9) (7,8) (2,3) (停止：所有點已經涵蓋) 5 C:\Documents and Settings\CWZu\桌面\2005_網路模式\課程資料更新\VRP\VEHICLE ROUTING PROBLEM(2006_rev).doc

Network Modeling Analysis Professor Anthony F. Han 5. Generalized Assignment Heuristic for VRP [Fisher & Jaikumar (1981)] Cluster First: Assign vehicles to a specific set of nodes. Route Second: Find TSP for each veh-route. Procedure: (設共有 k 部 veh; ki , k = 1,2,.... K ) (1) Select K “seed” point, each is covered by one veh. (2) Calculate jkd = the cost of inserting j into the route in which veh k travels from the depot directly to ki and back [ Min c c 0 0 c i o k c oi c i ] + + + + − c c j k ji k ( j 0 , j k + c i 0 k ) i k = j ik (3) Solve the generalized assignment problem depot Min s t . . d y jk jk N K j 1 = ∑∑ k 1 = ∑ a y j ≤ b k jk k = 1 ,..., K j K ∑ k = y 0 jk = 1 , ⎧ ⎨ K , ⎩ or 1 y jk = 0 j j = = N 1 2 , ,..., 0 (4) solve K 個 TSP RULES to determine the seed pints: high demand, e.g., (demand/capacity)>1/2. (1) Select those nodes which are either most remote from the depot, or with very (2) Make the K seed nodes properly scattered to cover the service area. 6 C:\Documents and Settings\CWZu\桌面\2005_網路模式\課程資料更新\VRP\VEHICLE ROUTING PROBLEM(2006_rev).doc

资料库

vrp网络模型的数学建模描述.pdf

相关推荐

网络技术

热门标签

最新资料