输电线找形分析的非线性有限元法.pdf-资料库

5 10 15 20 25 30 35 40 of Transmission Line Liu Zhendong, Liu Zhengshi HeFei 230009) (Noise and Vibration Engineering Research Institution,HeFei University of Technology, Abstract: IThe problem of transmission line’s form-finding is the basic for simulation and analysis of the transmission line structure. This paper introduced the catenary’s equation and parabolic equation of analytic method, as well as the equation of conductor sag. It derived general expression of stiffness matrix of nonlinear cable element in the form of total Lagrange by means of virtual work. The nonlinear finite element model in use of the three-node isoparametric cable element with torsional degrees-of-freedom was established. The finite element equation and the stiffness matrix were deduced. It was solved by the Newton-Raphson nonlinear iteration strategy. This method is relatively simple model, programming is easy to realize and high precision, convergence fast characteristic, also can be used for multi span, complex load situation. Considering the geometric nonlinearity and the torsional degrees-of-freedom, the calculation results with the actual working condition close, improve the accuracy of the analysis. The results of numerical examples show that the method is correct and reliable. Keywords: transmission line; form-finding; nonlinear finite element; cable structures 中国科技论文在线 http://www.paper.edu.cn 输电线找形分析的非线性有限元法# 刘振东，刘正士** （合肥工业大学噪声振动工程研究所，合肥 230009）摘要：输电线找形分析是输电线结构动力分析计算的基础。本文给出了解析法的悬链线方程和抛物线方程，以及相应的弧垂公式。通过虚功原理推导全 Lagrange 格式的非线性索单元刚度矩阵的一般表达式，采用具有转动自由度的三节点等参索单元来建立非线性有限元模型，推导出单元基本方程和单元切线刚度矩阵，利用 Newton-Raphson 非线性迭代法求解。这种方法具有模型较为简单，编程易于实现，计算精度高、收敛快的特点，也可以用于多跨、复杂荷载的情形。由于考虑了几何非线性和扭转自由度，因而计算结果与实际工况接近，提高了分析结果的准确性。算例结果表明该方法的正确和可靠。关键词：输电线；找形；非线性有限元；悬索结构中图分类号：TB121,TM752 Nonlinear Finite Element Method for Form-finding Analysis 0 引言输电线路导线是一种典型的悬索结构。根据索在安装时的张拉与不张拉，可将索分为三个力学状态，分别为放样后的无应力状态、自平衡的初始状态和外荷载作用下的工作状态 [1]。悬索结构在张拉前是松弛的，在外荷载的作用下可产生非线性大位移，对悬索结构找形前无法对其加载后的结果进行准确的分析和运算[2]。由于索本身没有刚度（除了抗拉刚度之外），也没有固定的形状，在给定的边界条件下，所施加的预张力和外部荷载需通过调节索的形状来保持平衡[3]，得到悬索结构的初始状态，即赋予悬索结构在初始状态下的应力和位移，才能进行后续的各种分析计算。因此，输电线路找形分析是输电线路微风振动、覆冰舞动、脱冰跳跃等动力分析的基础和前提[4]。对于找形问题的分析目前主要有解析法和非线性有限元法[5]，还有力密度法、动力松弛基金项目：高等学校博士学科点专项科研基金资助项目（2009011111006）作者简介：刘振东，（1988-），男，硕士研究生，主要研究方向：数字化设计与制造。通信联系人：刘正士，（1947-），男，合肥工业大学机械与汽车工程学院教授、博士生导师，主要研究方向：机器动态性能、噪声与振动控制、测试系统动力学。E-mail: liuzhengshi@gmail.com - 1 -

45 50 55 60 中国科技论文在线 http://www.paper.edu.cn 法以及能量法[6]。这些方法中的索段多为近似形状，所得解也多为近似解。针对这些不足，袁驷[3]提出了索结构找形分析的精确单元方法；侯景鹏等[7]采用 Newton-Raphson 迭代算法计算输电线在重力荷载下的初始形态；孟遂民等[8]分析得出了非均布荷载作用下，有限元法相对解析法更准确的结论。但两者都未考虑覆冰非圆截面下索的扭转自由度的影响。杨钦等[9] 总结出利用 ANSYS 对索结构进行非线性找形的步骤。因此，在输电线的找形方法中，非线性有限元法已成为解决问题最为广泛的途径。本文介绍了输电线找形的分析原理，由虚功原理出发推导全 Lagrange 格式的非线性索单元的一般表达式[10]，并采用具有转动自由度的三节点等参索单元[11]来建立非线性有限元模型，使其适用于更加复杂载荷的情形，推导单元基本方程和单元切线刚度矩阵，利用 Newton-Raphson 法求解。由于考虑了几何非线性和单元的扭转自由度，因而与实际更接近。使用 ANSYS 软件进行算例验证，表明该方法正确有效，可行性好。 1 导线初始构形分析原理为使问题简化，一般对输电线路导线计算采用如下假设：（1）索是理想柔性的，既不受压，也不抗弯；（2）索的材料符合胡克定律；（3）在不计风荷载、冰荷载的前提下，导线的荷载是均匀分布的；（4）导线垂度相比档距较小。和竖直分量，且图 1 为一输电线微元的隔离体，其中 H 和V 分别为输电线段截面上切向拉力T 的水平，正向按照弹性力学规定如图所示。 xq 和 yq 分别为沿 x 方向（线路方向）分布的水平和竖直载荷集度，正方向如图 1 所示。由水平和竖直方向的静力平衡条件，有： H dy dx V H = tan θ = ⋅ ∑ X = 0, ∑ Y = 0, dV dx + q y = 0, dH dx d dx + q x = 0 （1） H ⎛ ⎜ ⎝ dy dx ⎞ ⎟ ⎠ + q y = 0 （2） 65 在边界条件（给定某个边界张力）和载荷作用下，求解输电线的形状曲线 ( )y x 即为输电线的找形问题，上式即为其控制微分方程。在常见的实际工程问题中，输电线主要承受竖向载荷的作用。当 xq = 时，由方程（1）得 H 为常量。而方程（2）可写成 + q y = （3） 0 0 d yH 2 dx 2 70 75 图 1 输电线微段平衡关系图 Fig.1 The micro segment balance diagram of transmission line 方程（3）的物理意义是：索曲线在某点的二阶导数与作用在该点的竖向荷载集度大小成正比。应注意，在推导上述各方程时，荷载 xq 和 yq 的定义是沿跨度单位长度上的荷载，并且与坐标轴一致时为正。下面讨论两种竖向载荷的情形。 - 2 -

中国科技论文在线 1.1 竖向荷载沿跨度均布 http://www.paper.edu.cn 当竖向荷载沿跨度均布时，如图 2 所示，可推导出变形曲线为抛物线方程[5]，即： y = − x ) ( 4 fx l l 2 + c l x （4） 80 图 2 载荷沿跨度均布时的计算简图 Fig.2 Calculation sketch of the load distributed along the span 跨中垂度 f 与水平张力 H 的关系： H = 2 q l 0 f 8 1.2 竖向载荷沿输电线弧长均布（5） 85 当竖向载荷沿输电线弧长均布时，如图 3 所示，可推导出变形曲线为悬链线方程[5]，即： y = H q 0 ⎡ ⎢ ⎣ cosh − α cosh x 2 β l ⎛ ⎜ ⎝ − ⎞ α ⎟ ⎠ ⎤ ⎥ ⎦ （6）式中， = α sinh − ⎡ 1 ⎢ ⎣ c lβ ⎤ ⎥ sinh β ⎦ + β ， β= q l 0 H 2 。 90 95 图 3 载荷沿导线长均布时的计算简图 Fig.3 Calculation sketch of the load distributed along the wire 跨中垂度 f 与水平张力 H 之间的关系： f = H q 0 ⎡ ⎣ cosh α − cosh ( ) β α − − ⎤ ⎦ c 2 （7）输电线所受自身重力沿输电线长 S 方向均布，而不是沿跨度均布，因此输电线在重力作 l 小于1 8 时，一般按抛物线计算，即可用下的形状是悬链线而非抛物线。但是当垂跨比 f 得到足够精确的结果。 - 3 -

100 105 中国科技论文在线 http://www.paper.edu.cn 总的来说，用解析法求解输电线的找形问题只适用于简单均布载荷情形，在工程实际中，经常遇到的是多种载荷和复杂边界条件作用下的多跨输电线的找形问题。此时解析法并不适用，因此需要更加有效的方法求解该类问题。 2 输电线找形的非线性有限单元法解析法与有限元法都可以用来对输电导线进行平衡状态找形，其中，解析法不考虑结构的非线性过程，而以结构始态或终态为研究对象。有限元法则从始态开始，对非线性过程反复求解，逐步得到平衡终态。导线分析的有限单元法是将无限自由度问题转化为有限自由度问题。首先将导线离散成独立的杆段，然后通过合适的杆单元形函数建立单元刚度矩阵，再根据集成结构的总体刚度矩阵，建立整体结构节点位移向量和节点荷载向量之间的基本方程，通过引入边界条件，求解基本方程式解出节点位移。对于输电线的静态响应分析，需要知道索单元切线刚度矩阵和等效节点载荷向量的表达式。 2.1 不考虑转动自由度的全 Lagrange 格式非线性索单元一般表达式假设索单元变形前长度为 eL ，每单位长度质量为 m。变形后的构形以上标*标识，则变 110 形后单元内任一点坐标可表示为 ∗ X ∗= ( X S ) （8）其中，S 表示变形前单元的弧长坐标。进一步可表示为 ∗ X = [ ] N X ∗ N （9） 115 其中，[ ]N 为形函数矩阵， NX ∗ 为变形后单元节点坐标向量。对单元应用虚功原理，推导出不考虑转动自由度的全 Lagrange 格式的非线性索单元切线刚度矩阵的一般表达式[10]。单元切线刚度矩阵[ ]Tk [ k T ] = [ k E ] + [ ] k （10）其中，单元几何刚度矩阵[ { AE X = k [ ] L e ∫ E 0 ]Ek [ N T ∗ N ′ T ] [ ] N X ′ ∗ N } 1 − dS = L e ∫ 0 AE ε S [ N ′ T ] [ N dS ′ ] （11） 120 125 单元刚度矩阵[ ]k [ AE N [ ] k = L e ∫ ′ T ] [ N X X ∗ N ] ′ T ∗ N [ N ′ T ] [ N dS ] ′ 0 （12）上列式中， A 、 E 分别是变形前单元截面面积和弹性模量， Sε 是沿轴向变形方向的；将（ 9 ）式对弧长 S 求偏导 S X ∂ ⋅∂ S ∂ − T ∗ 0 ∗ Lagrange 应变， [ AE B T ] [ ] B dS L e = ∫ }1 2 { X = ∂ ε S ，其中，( )′ 表示对变形前弧长 S 的导数，[ ∗ ′ [ S ∂ = ] X N X ∗ ∂ N 表示矩阵的转置。 2.2 具有转动自由度的三节点空间索单元 B ] = X T ∗ N [ N ′ T ] [ N ′ ] ，( )T 输电线覆冰后，由于截面转动中心和总质心不重合，在力矩作用下会产生轴向扭转，若 - 4 -

中国科技论文在线 http://www.paper.edu.cn 130 要对覆冰输电线进行力学分析，就应采用具有转动自由度的索单元。 2.2.1 单元构形导线被离散成三节点等参单元（如图 4）。每个单元节点有 X、Y、Z 轴三个方向的平动自由度和一个绕导线轴线 S 的扭转自由度。相对初始构形的 X、Y、Z 轴平动方向的位移分别用 U、V、W 表示，相应地，绕 S 的扭转转角位移用θ表示。则单元节点的位移向量定义为下式 135 eq = [ U V W 1 1 1 θ 1 U V W 2 2 2 θ 2 U V W 3 3 3 θ 3 T ] （13） 140 145 150 单元内任一点的整体坐标和位移分别表示为 = ∑ X Y Z [ ] T 3 i 1 = [ N X i Y i i Z i T ] （14） Fig.4 The three-node isoparametric cable element with torsional degrees-of-freedom 图 4 具有转动自由度的三节点等参索单元上式右上标T 表示向量转置，下标数字表示单元中局部节点编号。单元上任意一点的坐标和位移可分别表示为 ] T θ = [ U V W ] N q [ e （15）其中插值函数矩阵[ ]N 为 [ N ] ⎡ = ⎣ [ ] N I 1 [ ] N I 2 [ ] N I 3 ⎤ ⎦ （16） [ ]I 是 4 4× 阶的单位矩阵，插值函数 iN 为 ) 24 20 25 22 N i i 6 i 6 ( ) ( − + − − = + S 2 2 i i 2 ⎞ ⎟ ⎟ ⎠ ⎛ ⎜ ⎜ ⎝ L e 这里的 eL 是单元长度。 2.2.2 单元的切线刚度矩阵[ ]Tk ⎛ ⎜ ⎜ ⎝ S 2 i ⎞ ⎛ + ⎟ ⎜ ⎟ ⎝ ⎠ L e i 5 − + 2 2 i ⎞ 3 ( 1,2,3) ⎟ ⎠ = （17）考虑转动自由度，其单元刚度矩阵为 ][ ] [ [ ] ∫ B D B dV k = ]B 可以表示为 [ 其中：单元应变矩阵 [ [ ] V T e = ] B - 5 - L e ∫ 0 = [ B 1 ] [ B 2 T [ A B D B dS ][ B 3 ] ] ，弹性矩阵 [ （18） ]D 为

中国科技论文在线 http://www.paper.edu.cn ∗ X ∂ S ∂ N ∂ i S ∂ ∗ Y ∂ S ∂ N ∂ i S ∂ ∗ Z ∂ S ∂ N ∂ i S ∂ 0 0 0 ⎤ 0 ⎥ ⎥ ⎥ Ni ∂ ⎥ ⎥∂ S ⎦ , ( i = 1,2,3 ) ， ] = B i ，[ ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ] X Y Z 155 [ D ] = 1 A AE B T B GJ T ⎡ ⎢ ⎣ ⎤ ⎥ ⎦ ∗ ∗ ∗ T T ⎤ = ⎦ [ Z Y ，上标 * 表示变形后的输电线构形。A ， X ⎡ ⎣ E 和GJ 分别是横截面积，杨氏弹性模量和裸导线的抗扭刚度； TB 是轴向变形和扭转变形的耦合参数。 [ U V W + ] T 单元几何刚度矩阵为其中 [ G ] I ⎡ ⎤ = ⎣ ⎦ diag [ ] I N ∂ 1 S ∂ ⎡ = ⎢ ⎣ [ 1 1 1 0 [ N ∂ 2 S ∂ 。 [ ] I ] eL 0 ] = ∫ Ek N ∂ [ ] I 3 S ∂ [ ⎤ ⎥ ⎦ T ] [ G S G dS ][ ] （23）， [ S ] = T I S ⎡ ⎤ ⎣ ⎦ T , S = AE ε S + B T Tθ ε + 0 ，偏心冰的重量产生的刚度矩阵[ ] iceK T ] N diag [ ⎤ ⎦ 式中， g 为重力加速度， zS 为覆冰输电线对 Z 轴的静矩。 0 0 0 k ice = − eL 0 ⎡ ⎣ ∫ g S [ ] [ z ] N dS （24） 160 165 至此，单元的切线刚度矩阵为 ] = [ ] k 2.2.3 单元外力向量和单元内力向量 k T [ + [ k E ] + [ k ice ] （25） xp ， yp ， zp 和 mθ分别表示作用在单元上的沿 X，Y，Z 和θ方向的分布载荷，则单 170 元等效节点载荷向量 ep 由下式计算 e p = eL 0 ∫ [ N T ] p x ⎡ ⎣ p y p m z θ T ⎤ ⎦ dS ，单元的外力向量 eP 为 e P = e p e + ，其中， er 是作用在单元节点上的集中载荷向量。 r 175 180 根据式（23），单元的内力向量 R X 0 k e E ] [ ⎡ ⎣ = Z ∗ 1 Y ∗ 1 X ∗ 1 ] 0 （26）上式没有考虑内力转矩，这是因为扭转变形是线性问题，一次计算即可求出转角，不需要迭代，因此不用考虑内力转矩。 ] [ B T S 0 ⎤ ⎦ Y ∗ 3 Y ∗ 2 dS X ∫ Z Z = 0 [ ∗ 3 ∗ 3 ∗ 2 ∗ 2 T T eL 0 2.2.4 迭代求解悬索结构通常表现出显著的几何非线性。对于这类问题的求解，Newton-Raphson 法[12] 被证明是有效的。用该方法迭代求解式[ ]Tk 、 qΔ 、P 和 R 分别是整体集成后的切线刚度矩阵、位移增量、外力向量和内力向量。第 i+1 次迭代后的位移为 q + = 1i 收敛，迭代过程可以终止。 + Δ 。当采用一种收敛准则，比值 Δ = − ，其中，[ q P R 小于某一给定的误差限时，即认为结果 1iq q + Δ ]Tk q i q - 6 -

中国科技论文在线 3 算例验证 http://www.paper.edu.cn 185 算例 1：为验证本文方法的准确性，利用算例验证，并且用解析法与 ANSYS 软件计算结果进行比较。利用文献[11]中的参数（表 1）和文献[13]中导线试验结果（在导线和覆冰重力作用下，导线中点的弧垂为 1.38m）对本文算法进行进一步的验证。表 1 单档输电导线的物理参数[11] Table.1 The physical parameters of single transmission line 参数轴向刚度扭转刚度水平拉力裸导线直径水平档距单位长度质量符号 AE GJ H d xL μ 数值 13.3 101 21.73 18.8 125.9 1.53 单位 610 N 2 Nm rad − 1 310 N 310 m− m kgm− 1 输电线路在重力载荷的作用下是典型的非线性大位移、小应变问题，所以在 ANSYS 计算时需要做一些必要的处理[14]。在 ANSYS 中，以杆单元 BEAM188 为索单元离散模型，该单元通过操作 KEYOPT1 释放其对应的弯曲变形自由度，以模拟张紧索或松弛索，覆冰冰型为 D 型（图 5），导线两端等高。应注意的是，初应变是基于无应力时的索长和当前索长（两节点之间的距离）计算，假设本例的初应变为 0。由式（5）、（7）可知，索的垂度和水平张力互为结果，即索的线形为一悬链线族或抛物线族，必须已知其中一个参数才能唯一确定索的线形或张力。本文考虑其收敛速度和计算时间，在此使用直接迭代法，以索中点的初始水平张力为收敛条件。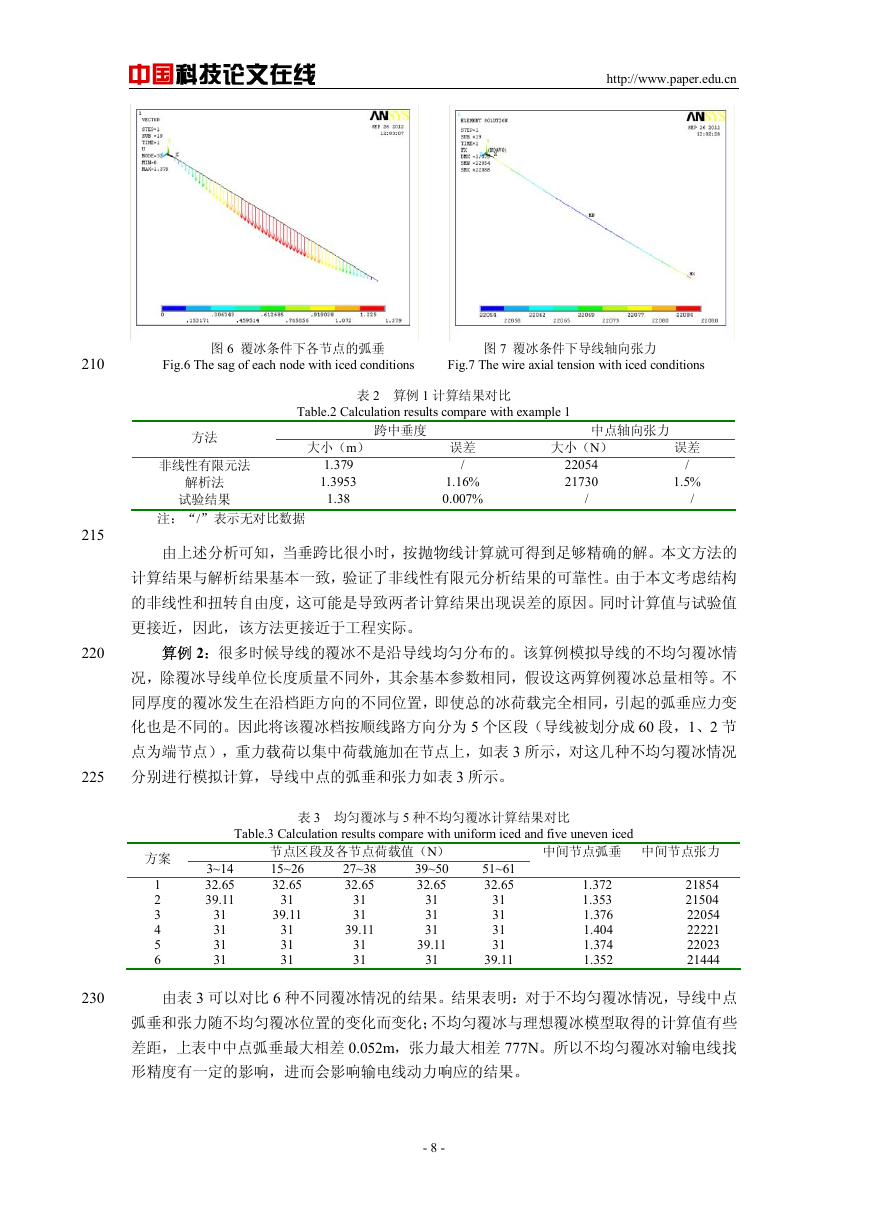 190 195 200 205 图 5 覆冰输电线截面形状 Fig.5 The cross-section shape of iced transmission line 图 6 为导线覆冰重力作用下节点弧垂的 ANSYS 计算结果。根据式（4）~（7）求得初 10m s ）为：悬链线解 1.3953m；抛物线解为 1.3951m，始状态的跨中垂度（取重力加速度为与悬链线解很接近，误差仅为 0.014%；ANSYS 解为 1.379m（如图 5 所示），与悬链线的误差为 1.16%，与文献[13]的误差仅为 0.007%。图 6 所示为迭代求解后导线的轴向张力，导线中点的轴向张力为 22054N，此时与初始水平张力的差为 324N，误差为 1.5%。 2 - 7 -

中国科技论文在线 http://www.paper.edu.cn 210 图 6 覆冰条件下各节点的弧垂图 7 覆冰条件下导线轴向张力 Fig.6 The sag of each node with iced conditions Fig.7 The wire axial tension with iced conditions 表 2 算例 1 计算结果对比 Table.2 Calculation results compare with example 1 方法非线性有限元法解析法试验结果大小（m） 1.379 1.3953 1.38 215 注：“/”表示无对比数据跨中垂度中点轴向张力误差 / 1.16% 0.007% 大小（N） 22054 21730 / 误差 / 1.5% / 由上述分析可知，当垂跨比很小时，按抛物线计算就可得到足够精确的解。本文方法的计算结果与解析结果基本一致，验证了非线性有限元分析结果的可靠性。由于本文考虑结构的非线性和扭转自由度，这可能是导致两者计算结果出现误差的原因。同时计算值与试验值更接近，因此，该方法更接近于工程实际。 220 算例 2：很多时候导线的覆冰不是沿导线均匀分布的。该算例模拟导线的不均匀覆冰情况，除覆冰导线单位长度质量不同外，其余基本参数相同，假设这两算例覆冰总量相等。不同厚度的覆冰发生在沿档距方向的不同位置，即使总的冰荷载完全相同，引起的弧垂应力变化也是不同的。因此将该覆冰档按顺线路方向分为 5 个区段（导线被划分成 60 段，1、2 节点为端节点），重力载荷以集中荷载施加在节点上，如表 3 所示，对这几种不均匀覆冰情况分别进行模拟计算，导线中点的弧垂和张力如表 3 所示。 225 方案表 3 均匀覆冰与 5 种不均匀覆冰计算结果对比 Table.3 Calculation results compare with uniform iced and five uneven iced 中间节点弧垂中间节点张力 3~14 32.65 39.11 31 31 31 31 节点区段及各节点荷载值（N） 39~50 15~26 32.65 32.65 31 31 39.11 31 31 31 39.11 31 31 31 27~38 32.65 31 31 39.11 31 31 1 2 3 4 5 6 由表 3 可以对比 6 种不同覆冰情况的结果。结果表明：对于不均匀覆冰情况，导线中点弧垂和张力随不均匀覆冰位置的变化而变化；不均匀覆冰与理想覆冰模型取得的计算值有些差距，上表中中点弧垂最大相差 0.052m，张力最大相差 777N。所以不均匀覆冰对输电线找形精度有一定的影响，进而会影响输电线动力响应的结果。 21854 21504 22054 22221 22023 21444 1.372 1.353 1.376 1.404 1.374 1.352 51~61 32.65 31 31 31 31 39.11 230 - 8 -

资料库

输电线找形分析的非线性有限元法.pdf

相关推荐

开发技术

热门标签

最新资料