logo资料库

应用时间序列分析习题答案（王燕编著）.docx

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.29M 资料格式：docx 举报 版权申诉
第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
资料共11页，剩余部分请下载后查看
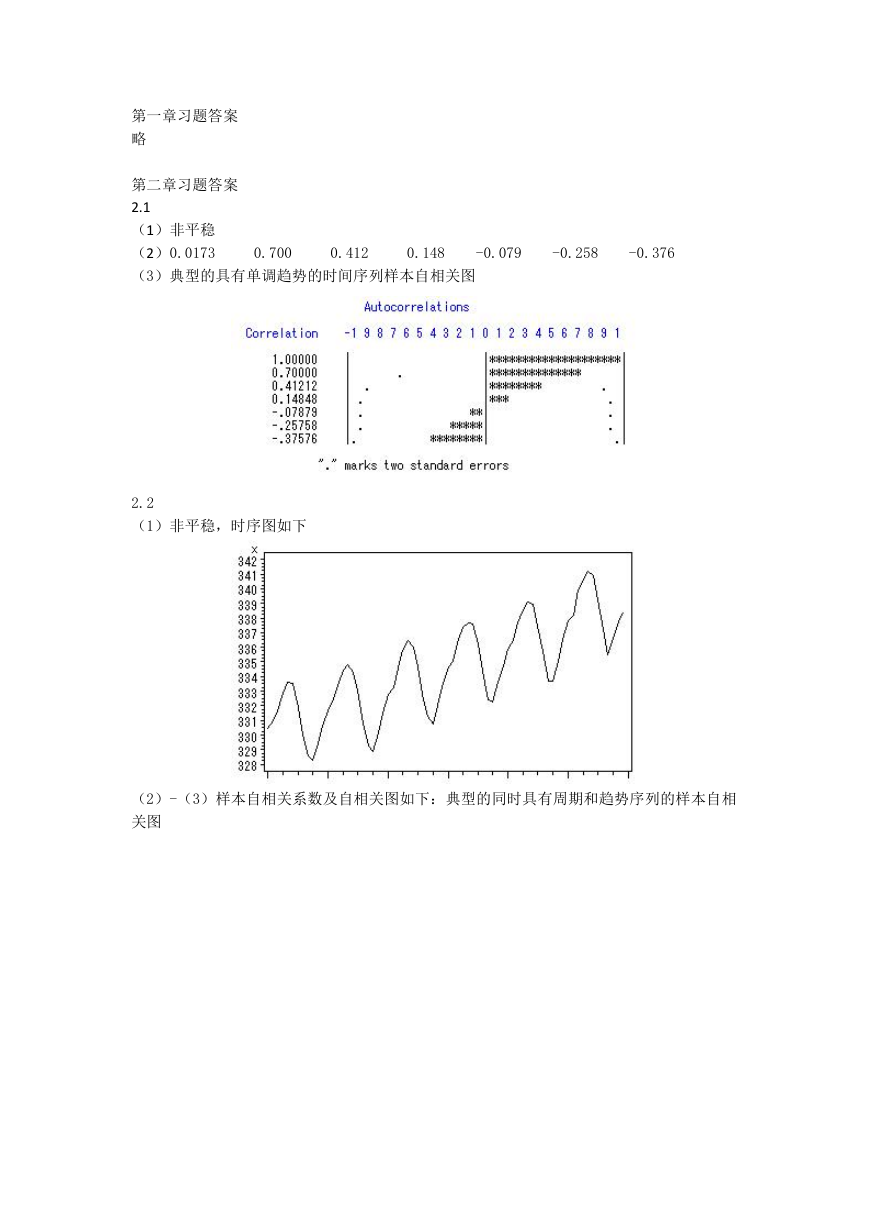
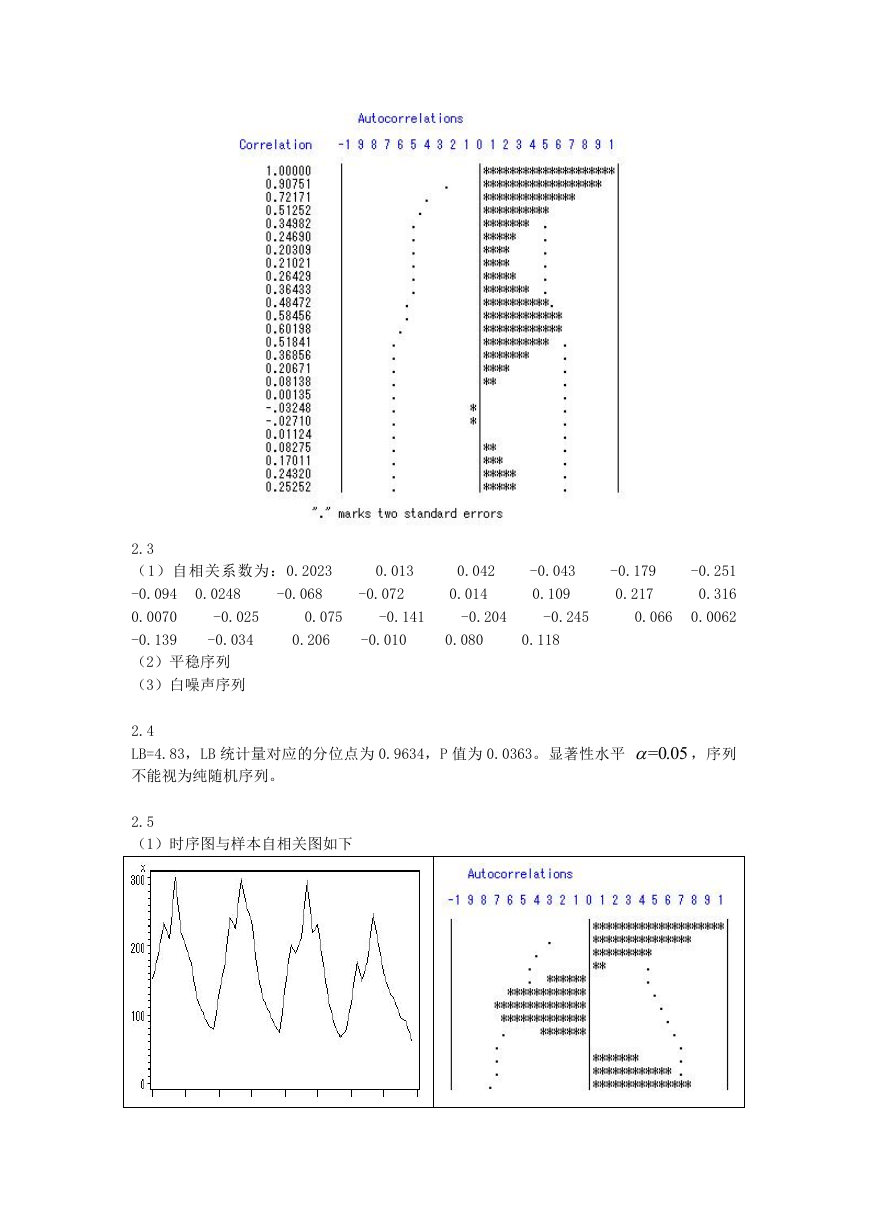
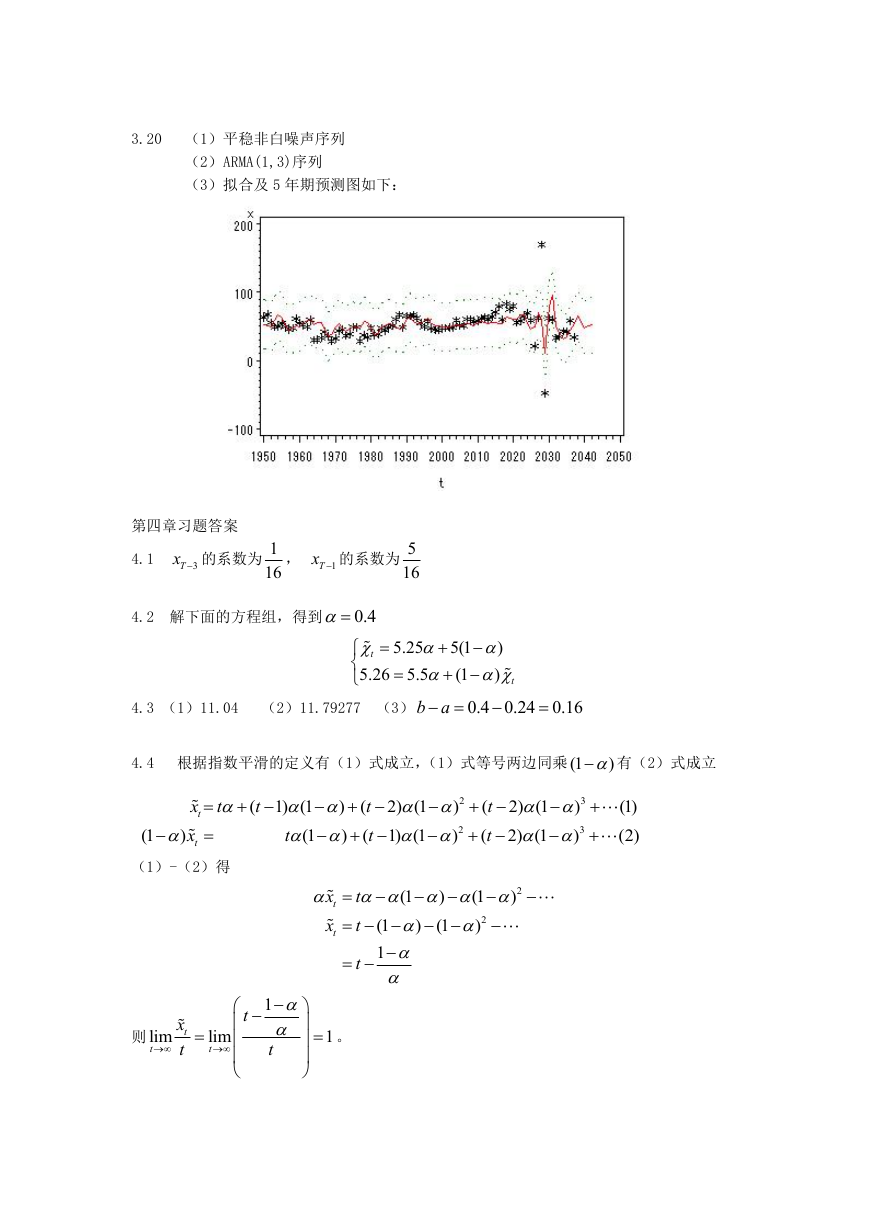
    第一章习题答案 略 第二章习题答案 2.1 （1）非平稳 （2）0.0173 （3）典型的具有单调趋势的时间序列样本自相关图 0.148 0.700 0.412 -0.079 -0.258 -0.376 2.2 （1）非平稳，时序图如下 （2）-（3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相 关图
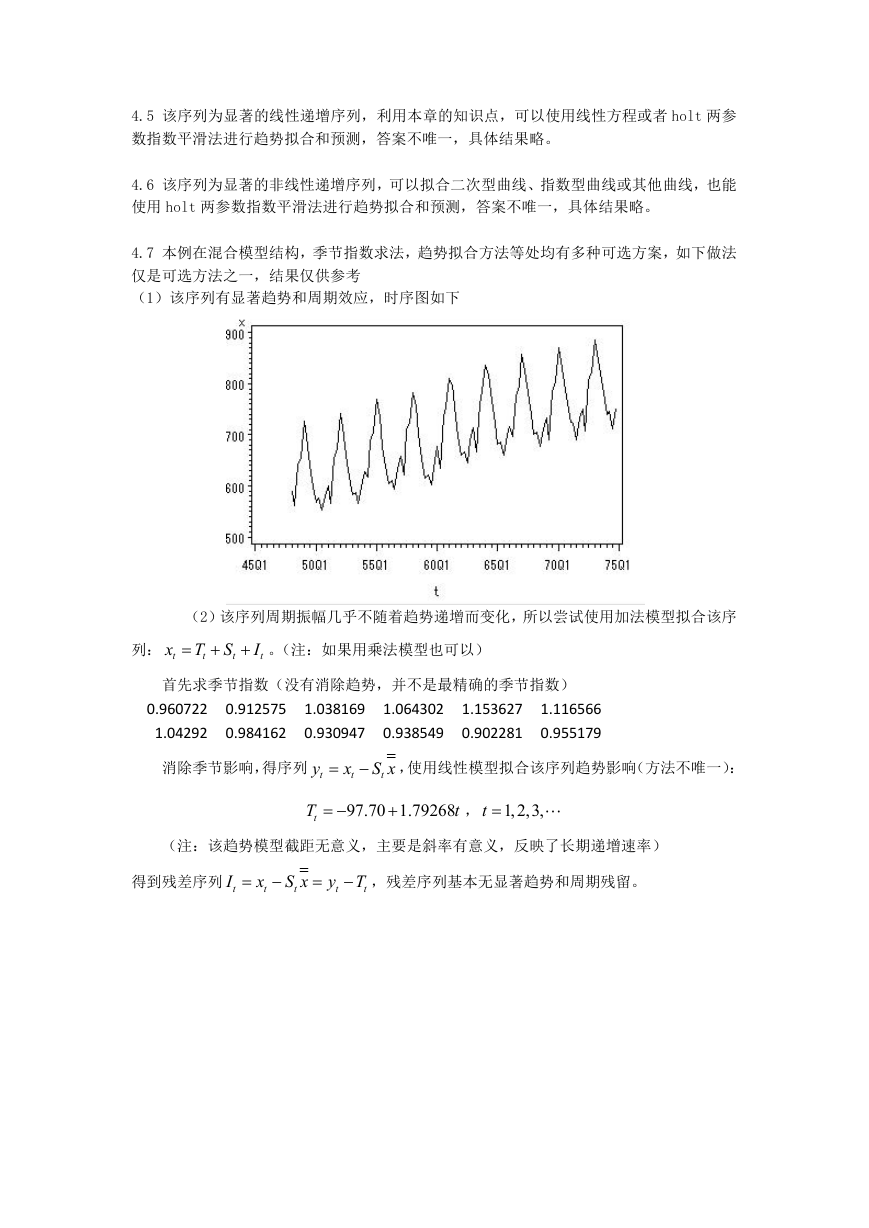
    0.0248 -0.068 0.075 2.3 （1）自相关系数为：0.2023 -0.094 0.0070 -0.139 （2）平稳序列 （3）白噪声序列 -0.025 -0.034 0.206 0.013 -0.072 0.042 0.014 -0.043 0.109 -0.179 0.217 -0.141 -0.204 -0.245 0.066 -0.251 0.316 0.0062 -0.010 0.080 0.118 2.4 LB=4.83，LB 统计量对应的分位点为 0.9634，P 值为 0.0363。显著性水平 =0.05 不能视为纯随机序列。 ，序列 2.5 （1）时序图与样本自相关图如下
    （2） 非平稳 （3）非纯随机 2.6 （1）平稳，非纯随机序列（拟合模型参考：ARMA(1,2)） （2）差分序列平稳，非纯随机 第三章习题答案 3.1 ( ) 0 tE x  , Var x  ( ) t 1 1 0.7  2  1.96 ,   2 2 0.7  0.49 0  , 22 3.2   1 7 15   , 2 1 15 3.3 ( ) 0 tE x  , ( Var x t )  (1 0.15)(1 0.8 0.15)(1 0.8 0.15)     1 0.15    1.98  0.70  , 2  1 0.8  0.15 0.41   , 3  0.8  2  0.15  1  0.22   1 0.8 1 0.15    11 1  0.70 3.4 1 0c    , 3.5 证明:   , 22 2   0.15 0  , 33  1 ,    1 1 c         1 k k  c k , k  2  2 该序列的特征方程为： 3     ，解该特征方程得三个特征根： 2- -c c 0 1 1  ， 2 c  ， 3    c 无论 c 取什么值，该方程都有一个特征根在单位圆上，所以该序列一定是非平稳序列。证毕。 3.6 (1)错 （2）错 （3）对 （4）错 （5） 3.7 该模型有两种可能的表达式： x   1 t t   t 1 2 和 12 x   t t   t 。 3.8 将 x t  10 0.5  x t 1    t  0.8  t  2  C  t  3 等价表达为
    x t  20 3  2 1 0.8 B CB   1 0.5 B   2 1 0.8    B CB  t  3 (1 0.5  B  2 0.5 B 2  3 0.5 B 3 )   t 展开等号右边的多项式，整理为 0.5  0.8  1 0.5  B 2 2 B 2 B 3 B 3 0.5  0.8 0.5   3 CB  3 B 4 4 0.5  0.8 0.5  4 0.5  B  CB 2 4 B       合并同类项，原模型等价表达为 x t  20 [1 0.5   B  0.55 B 2    k  0 k 3 0.5 (0.5  0.4  3  C B  t ) ] k 当 30.5  0.4  0C  时，该模型为 (2)MA 模型，解出 C  0.275 。 3.9 Var x   ) 1 0.7 ( 2  2 0.4  t   0.59   ， 2  0.24 ，   k 0, k  3 ( ) 0 tE x  ,  1.65  1   0.7 0.7 0.4  1.65 0.4 1.65 3.10 （1）证明：因为 ( Var x t )  lim(1 k   kC 2 2 )    ，所以该序列为非平稳序列。 y t  x t  x t 1   ( C t   1)  1 t  （2） ，该序列均值、方差为常数， ( ) 0 tE y  , ( Var y t )   1 ( C   2  1) 2    自相关系数只与时间间隔长度有关，与起始时间无关  1  1 C  1 ( 1) C   ,  k 2  0, k  2 所以该差分序列为平稳序列。 3.11 （1）非平稳，（2）平稳，（3）可逆，（4）不可逆，（5）平稳可逆，（6）不平稳不可逆 3.12 1G  ， 1 G 0  G  1 1  0  0.6 0.3 0.3 G  ， k   G  1 k 1   1 k   G 1 1  1 0.3 0.6 ,   k k  2  0.3 0.6k  1 t k    k  0 所以该模型可以等价表示为： x  t t   3.13    0    2 1 1   3 1 1 0.25    12
    3.14 证明：已知 1   ， 1   ，根据 ARMA (1,1) 模型 Green 函数的递推公式得：  0.5 0.25   ， 2  1 G k  G  1 k 1   k  1 1  G 1  k  1 1  , k  2 1 2 G  1 1  0 1 4 1G  ， 0 G 1  1  0  1   k    j  0   j  0 G G j j 1  2  1   1  G 2 j   2  1 1  j   2(  1 j 1  j  3 2  1   j 1)  1  5  1 4 2 5 1       1 1 1 4 2 4     1 1 1 2   1   2 1 1  1  7 26  0.27   j  0 G G j j k   G 2 j   j  0   j  0 G j   1 G 1 j k      j  0 G 2 j   1   j  0 G G j 1 j k     j  0 G 2 j   1 k 1  , k  2 3.15 （1）成立 （2）成立 （3）成立 （4）不成立 3.16 （1）95%置信区间为（3.83,16.15） （2）更新数据后 95%置信区间为（3.91,16.18） 3.17 （1）平稳非白噪声序列 （2）AR(1) (3) 5 年预测结果如下： 3.18 （1）平稳非白噪声序列 （2）AR(1) (3) 5 年预测结果如下： 3.19 （1）平稳非白噪声序列 （2）MA(1) (3) 下一年 95%的置信区间为（80.41,90.96）
    3.20 （1）平稳非白噪声序列 （2）ARMA(1,3)序列 （3）拟合及 5 年期预测图如下： 第四章习题答案 4.1 3Tx  的系数为 1 16 ， 1Tx  的系数为 5 16 4.2 解下面的方程组，得到  0.4 5(1 5.25 )        t  (1 5.26 5.5 )        t 0.4 0.24 0.16 b a    4.3 （1）11.04 （2）11.79277 （3） 4.4 根据指数平滑的定义有（1）式成立，（1）式等号两边同乘 (1 ) 有（2）式成立 x  t x  t   (1  )  t    ( t 1) )   ) t   (1  (1  ( t   ( t   2 ) 2)   2 ) 1)   (1 (1   ( t   ( t   3 ) 2)   3 ) 2)   (1 (1       (1) (2) （1）-（2）得   2 t t x  t x  t )        (1  2 )   (1 )     (1 (1 )       1      t 则 lim t  x  t t  lim t     1 t  t           1 。
    4.5 该序列为显著的线性递增序列，利用本章的知识点，可以使用线性方程或者 holt 两参 数指数平滑法进行趋势拟合和预测，答案不唯一，具体结果略。 4.6 该序列为显著的非线性递增序列，可以拟合二次型曲线、指数型曲线或其他曲线，也能 使用 holt 两参数指数平滑法进行趋势拟合和预测，答案不唯一，具体结果略。 4.7 本例在混合模型结构，季节指数求法，趋势拟合方法等处均有多种可选方案，如下做法 仅是可选方法之一，结果仅供参考 （1）该序列有显著趋势和周期效应，时序图如下 （2）该序列周期振幅几乎不随着趋势递增而变化，所以尝试使用加法模型拟合该序 x 列： t  T t  S t  。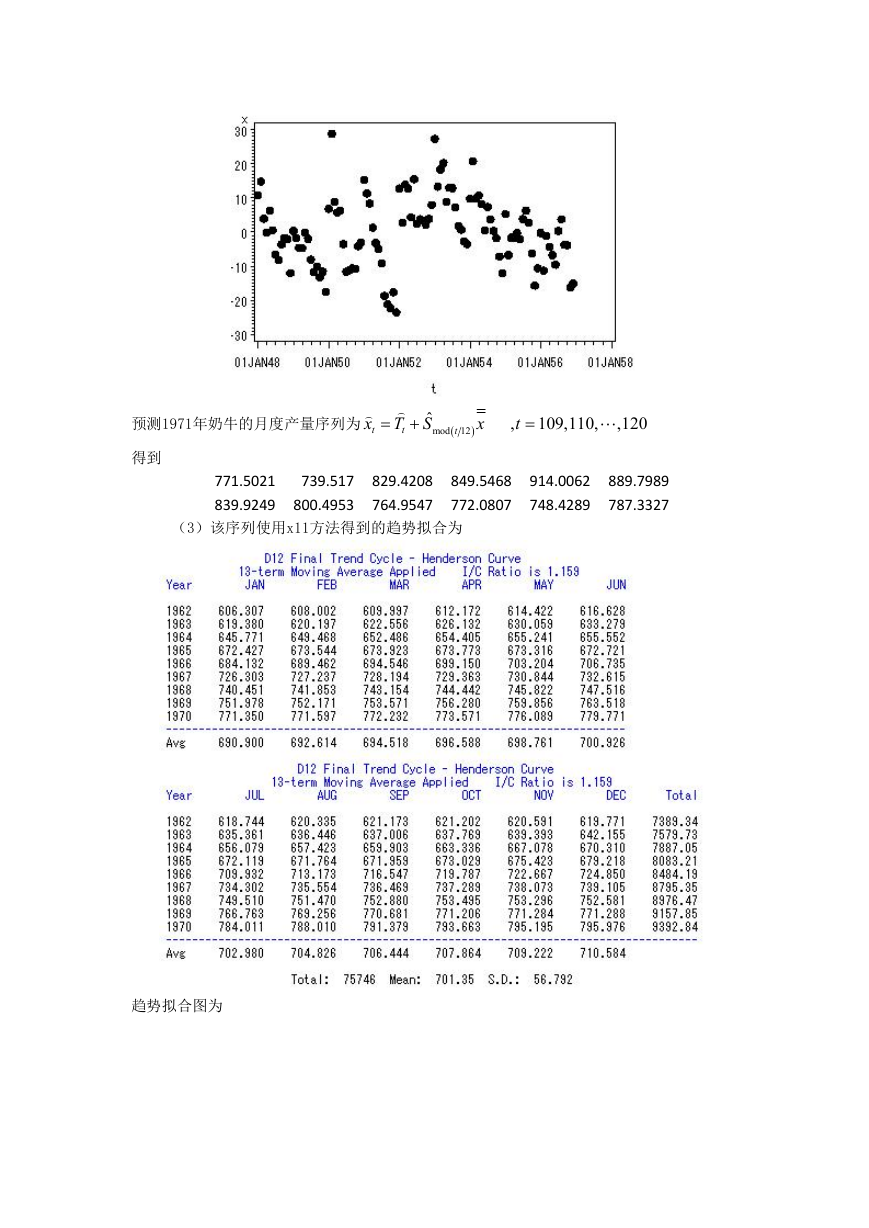（注：如果用乘法模型也可以） I t 首先求季节指数（没有消除趋势，并不是最精确的季节指数） 0.960722 1.04292 0.912575 0.984162 1.038169 0.930947 1.064302 0.938549 1.153627 0.902281 1.116566 0.955179 y 消除季节影响，得序列 t  x t  ，使用线性模型拟合该序列趋势影响（方法不唯一）： S x t tT   97.70 1.79268 t  ， 1,2,3, t   （注：该趋势模型截距无意义，主要是斜率有意义，反映了长期递增速率） I 得到残差序列 t  x t  S x t  y t T  ，残差序列基本无显著趋势和周期残留。 t
    预测1971年奶牛的月度产量序列为  x t  T t   ˆ S mod  t 12  x , t  109,110,  ,120 得到 771.5021 839.9249 739.517 800.4953 829.4208 764.9547 849.5468 772.0807 914.0062 748.4289 889.7989 787.3327 （3）该序列使用x11方法得到的趋势拟合为 趋势拟合图为
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料