具有关节柔性/臂杆柔性机械臂的位置内环阻抗控制.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.33M 资料格式：pdf 举报版权申诉

weixin_38614287-12091432-4744300845376933627.pdf-第1页.png

第1页 / 共7页

weixin_38614287-12091432-4744300845376933627.pdf-第2页.png

第2页 / 共7页

weixin_38614287-12091432-4744300845376933627.pdf-第3页.png

第3页 / 共7页

weixin_38614287-12091432-4744300845376933627.pdf-第4页.png

第4页 / 共7页

weixin_38614287-12091432-4744300845376933627.pdf-第5页.png

第5页 / 共7页

weixin_38614287-12091432-4744300845376933627.pdf-第6页.png

第6页 / 共7页

weixin_38614287-12091432-4744300845376933627.pdf-第7页.png

第7页 / 共7页

文本预览

5 10 15 20 25 30 35 40 中国科技论文在线 http://www.paper.edu.cn 具有关节柔性/臂杆柔性机械臂的位置内环阻抗控制# 任珊珊，贾庆轩，褚明** （北京邮电大学自动化学院，北京 100876）摘要：空间机械臂在执行任务时，为了保证任务的精确性，对运动轨迹和接触力都有一定的要求，同时机械臂的本体结构会对控制效果造成一定的影响。为此，本文考虑关节柔性/臂杆柔性的影响，采用 Kane 方程建立机械臂动力学模型并设计位置内环阻抗控制器。同时，在 Matlab/Simulink 中搭建阻抗控制仿真平台，对比分析关节柔性/臂杆柔性机械臂在斜面运动时对常规阻抗控制算法与位置内环阻抗控制算法的响应。仿真结果表明，柔性特性的存在会引起臂杆的变形，所设计的位置内环阻抗控制器可以实现柔性机械臂的轨迹跟踪和接触力控制。关键词：柔性机械臂；动力学；位置内环阻抗控制中图分类号：TP273.5 Position inner loop impedance control of flexible links and flexible joints REN Shanshan, JIA Qingxuan, CHU Ming (Automation School, Beijing University of Posts and Telecomunications,Beijing 100876) Abstract: When space robot arm implements the task, there is a certain requirement to track and contact force in order to ensure the accuracy of the mission, and the structure of the robot arm also affects the controlling effect. For this reason, considering the effect of joint flexibility / link flexibility ,we establish the dynamics model by Kane equation and design inner loop impedance controller.Meanwhile, the control simulation platform is established in MATLAB/Simulink. And we compare and analyse the response of the joint flexibility / link flexibility manipulator to the conventional impedance control algorithm and the position inner loop impedance control algorithm for the motion on the inclined plane. The simulation results show that flexibility of characteristics can cause jitter to some degrees. The position inner loop impedance controller can realize the trajectory tracking and contact force control of the flexible manipulator. Key words: flexible manipulator; dynamics;position inner loop impedance control 0 引言随着空间技术的快速发展，利用机械臂辅助航天员完成各种操作已成为研究热点，空间机械臂长宽比相对较大一般视为细长杆，在运行过程中会产生弹性变形，同时关节内的谐波减速器以及力矩传感器等柔性元件的存在使关节产生柔性变形。运动过程中关节柔性/臂杆柔性的弹性变形耦合，会给机械臂的主动控制造成困难，需要设计一种考虑关节柔性/臂杆柔性的控制器。阻抗控制作为一种有效的机械臂柔顺控制，已被逐步运用到各个领域。Hongan[1]，在 1987 年提出机器人阻抗控制，将自由运动空间和约束运动空间纳入统一的控制框架后，许多学者对阻抗控制进行了研究。文献[2]针对机器人与环境接触作业的需求，设计了自适应阻基金项目：国家自然科学基金资助项目（51305039）作者简介：任珊珊（1990-），女，硕士研究生，空间机器人技术通信联系人：褚明（1983-），男，副教授，主要研究方向：机器人动力学与控制. E-mail: chuming_bupt@bupt.edu.cn - 1 -

45 50 55 中国科技论文在线 http://www.paper.edu.cn 抗控制器，针对环境不确定性，采用平面两连杆柔性机械臂在含有三角形凹陷环境表面的接触运动进行分析。危清清[3]提出柔性机械臂辅助大负载空间舱段对接的阻抗控制方法，采用拉格朗日法推导了空间机械臂的关节输入力矩作为前馈输入，建立含动力学前馈的空间机械臂阻抗控制程序，同时进行了直线运动仿真和随动运动仿真。文献[4]徐国政针对机器人辅助患肢主动康复训练过程中辅助力/阻力不能随患肢病情实时调整的问题，提出了一种新的模糊自适应阻抗力控制方法，表明阻抗控制方法对力控的有效性。Payam Zarafshan[5]针对具有柔性关节和柔性太能电池板空间机器人系统建立动力学模型并划分为两个刚性体和柔性体的运动，同时采用阻抗控制对平面两自由度柔性关节机械人运动过程中的轨迹进行控制仿真，最终证明了控制器的稳定性。Zhao-Hui Jiang[6]提出一种针对机械臂末端轨迹控制的阻抗控制，使实际目标阻抗跟踪理想阻抗模型，同时对于参数不确定性，设计自适应阻抗控制，并采用两连杆柔性机械臂证明所提出方法的有效性。但对于同时存在关节柔性和臂杆柔性的空间机械臂尚未有相关的成果报道。本文针对柔性臂杆机械臂动力学模型，设计接触操作阻抗控制，提出一种适用于关节柔性和臂杆柔性并存的位置内环阻抗控制算法，并且搭建 Smulink 控制仿真平台，采用两连杆机械臂模型进行仿真验证，给出柔性机械臂的控制响应，证明所设计阻抗控制控制算法的有效性。 1 关节柔性/臂杆柔性两连杆机械臂动力学建模如图 1 所示，为两连杆柔性关节柔性臂杆机械臂示意图，包含两个柔性关节和两个细长 60 臂杆。图 1 柔性关节/柔性臂杆机械臂示意图 Fig. 1 Joint flexibility / link flexibility manipulator structure 关于柔性关节建模简化方面，Spong[7]最先提出了柔性关节的简化模型，Readman[8]在此基础上进行修正给出了完整模型。本文在建模过程中，忽略谐波减速器之间齿轮的摩擦及变形影响，只考虑其中的机械动力学，不考虑其中电气动力学产生的影响，将柔性关节简化为介于电机转子和连杆之间的线性扭转弹簧。空间机械臂的长度和直径的比值相对较大，在大范围的运动中会产生柔性变形，在考虑臂杆变形方面，采用假设模态法对变形量进行描述。根据上述简化描述采用 Kane 方法进行动力学模型的建立，Kane 方法通过引入偏角速度和偏线速度的概念，对于多自由度复杂系统的动力学推导计算比较有利，例如机器人、空间机械臂、各种航天器等等，为动力学的建模提供了一种新的途径。由质点系 Kane 方程，选取柔性关节/柔性臂杆机械臂的广义坐标为 { = ，则有，其中， m1θ 、 m2θ 为电机转角， 1N 、 2N 为减速比， 1θ、 2θ， 1q 、 2q 分 α θ 1 m1 α α θ θ 1 2 / N 1 / N α θ m2 、 2 = q 1 } q 2 = y 2 1 2 别表示关节转角和模态坐标。 F yi ∗+ F yi = i 0 ( = 1,...,6) （1） - 2 - 65 70 75

中国科技论文在线 ∗ = F yi http://www.paper.edu.cn = 1,2) （2） v a m j d ( i pj j p  τ (1 m ε k (1 − ε k (3 ∂ u 4 ∂ x 4 EI   =      ≤ ≤ i ≤ ≤ i ≤ ≤ i 2) 2) 4) (3 ≤ ≤ i 6) F yi 其中， i pjv 表示臂杆任意一点对广义坐标的偏速度， j （3） pa 表示臂杆上任意一点的加速度，τ − 表示关节线性扭变形角， EI 为截面的表示电机驱动力矩， k 表示线性扭簧刚度， ε α θ= 弯曲刚度， yiF 分别表示为电机驱动力、柔性关节内力、柔性臂杆内力产生的广义主动力， * yiF 表示广义惯性力。如图 1 所示，P 表示连杆上任意一点的位置 i r i = + ， ( , ) iu x t u r i i x q tϕ= ( ) ( ) 表示弹性变形，对其求导可以得到任意一点的速度，进而对任意广义坐标求解偏导得到各个坐标所对应的偏速度，带入到上式（2）可分别求解出柔性机械臂的广义惯性力，结合广义主动力公式（3），最终由 Kane 方程（1）建立柔性关节/柔性臂杆机械臂动力学方程，去除高阶耦合项后，动力学方程可写为如下形式： M  θ θ  q ( , )( , ) θ τ τ q ( , ) ext = + H + q （4）       θ θ +  C q q ( , , ) , + = α τ τ  J m m − = τ α θ k ( ) 80 85 90 95 上式（4）动力学方程可简写为：其中， p qθ= ( , ) p + +  p  M C p （5）， mJ 为电机转动惯量， M 、 C 、 K 分别为广义质量矩阵、广义阻 Q + J F ext K p T = 尼矩阵、广义刚度矩阵。Q 为广义列矩阵。 2 考虑关节柔性/臂杆柔性的动力学建模机械臂在辅助宇航员进行太空作业过程中，受到外界环境的约束，不仅要进行精确的位置控制，还要恰当进行力控制，避免过大冲击力损害外部舱体或者机械臂本体。为了满足这种要求，本文采用笛卡尔空间位置内环的阻抗控制算法。阻抗控制提供一个对自由运动空间和约束空间进行统一的控制框架，将接触力作为机械臂末端的期望位置与环境约束下的实际位置偏差的信息源，建立机械臂末端的位置偏差和接触力的动态关系，使机械臂在约束环境中运动时保持适当的接触力，通过调整反馈位置误差、速度误差或刚度来达到对对机械臂末端轨迹的跟踪以及对末端接触力的控制，对此本文采用二阶目标阻抗模型： 100 其中： dM 为目标惯性、 dB 为目标阻尼、 dK 为目标刚度。 )− dX 表示末端期望目标位置， X 表示实际位置， ext F 所受到的作用力， eK 为环境刚度。 K X = ( e d M d  E +  E B d + K d = E F e （6） d= X 表示位置误差， E X X 为机器人末端与环境接触 − 105 针对动力学公式（4）利用关节转角对电机转角进行表示可得： + − k Mp k C p p H p ( 1 = α ))  + + −  ( ( ) , − 1 T − k J F ext 1 θ （7） - 3 -

中国科技论文在线 http://www.paper.edu.cn 则针对公式（7）分别进行求导可得电机转角的角速度和角加速度，得到动力学公式中关于关节转角的表达：   Mp  + θ )   Mp T p ( ) J m − k k J 2  F ext ( − 1 + + k − 1 − 1  = − 1 + k +   Mp + Mp C p ( , − 1 k C ( +  p ) (  p , K p ( ) − +   p H p )) ) ( − T J p F ( ) ext  p ( ) F ext − k 2 − 1 T J  p ( )  F ext （8） T k = − 1 J τ m 110 根据笛卡尔空间坐标 x f p ( ) J p ，由雅可比矩阵的定义可得 ( ) = f p ( ) / ∂ ，关节空间 p ( ) 与操作空间的转换关系通过雅克比公式进行转化： = x J p p ( ) +  J p p ( )  x 最终可得到位置内环阻抗控制律： − 1 =  （9）   （10） J p p ( ) 其中， = u k p ( x f − x ) τ = J + J − k M p 1 ( − f m k x ( d ) (  ， f x ) x − p u ) x= d −  β F 3 ext + G p ( ) （11）  β β − F F 1 ext 2 ext − E ， T T , ) = + = J = p ) ( C p ( − J K J 1 m +  p H p ( ) β  ， p ( ) 2 + − 1 J k C ( m β 1 G p ( 本文所设计的阻抗控制算法与文献[9]针对刚性机械臂阻抗控制相比增加了位置内环以及柔性关节柔性臂杆因素，引入了臂杆的模态坐标及考虑了臂杆变形的影响。根据式（11）可以得到阻抗控制流程图，如图 2 所示。 p )  p Mp H ( − mJ K J 2 1   p p H ) , ( = − mJ k J 1  +   Mp β 3 − 1 p ) +   Mp + ) 2 J k m J k m ( + ， )) + − 1 ) ( T T  (  p 115 120 图 2 位置内环阻抗控制结构图 Fig. 2 Position inner loop impedance control structure 125 130 其中，位置内环采用 PD 控制， pk 代表比例系数， dk 代表微分系数。当机械臂未与外界物体 x= 机械臂的实际位置跟踪，同时当机械臂末端与外界环境接触接触时，此时 F 为零， f x 时，产生接触力，提供位置修正量的信息源，达到控制的目的。 3 基于 Simulink 平台的仿真实验 d 为了验证所提出的计入关节柔性/臂杆柔性阻抗控制算法的有效性，以空间两连杆柔性机械臂为对象，对比分析机械臂对常规阻抗控制控制算法与位置内环阻抗控制算法的响应，其中柔性机械臂的基本参数如表 1 所示。 - 4 -

中国科技论文在线 http://www.paper.edu.cn 135 Tab. 1 Joint flexibility / link flexibility manipulator parameter 表 1 柔性关节/柔性臂杆机械臂参数项目指标项目指标机械臂杆参数机械臂臂杆密度 2.7 10× 3 kg/m3 关节关节转动惯量 0.75 10−× 4 Kg.m2 模态刚度 11.36N.m2 参数电机转动惯量 4 0.106 10−× Kg.m2 臂杆长度 1m 关节刚度 7500Nm/rad 横截面积 1.2 10−× 4 m2 减速比 100 基于 System Function 函数在 Matlab/Simulink 中搭建位置内环阻抗控制算法，采用定步长四阶龙格库塔法，其中仿真步长设置为 0.01s，仿真时间为 5s。机械臂的初始关节位置为 1= / 2θ π ， 2 =- θ π ，关节初始角速度为 0。在仿真过程中机械臂期望的运动轨迹为式（12），期望的接触力为 5N。 / 2      = x d = y d 2 10 2 10 + + t t 2 2 2 2 （12）根据阻抗控制参数的获取三种方法，通过自适应方法在线获取阻抗控制参数，通过神经网络学习方法获取和从示教数据获得阻抗控制参数。本文第三种方法获取，经过多次仿真实验，调整阻抗控制参数。本文取 pk 为 5， dk 为 12，同时控制参数为： = = 。 = M d 1 0 0 1    K ， d 123   0  14   0  0 14    0   123  B ， d    图 3 为机械臂末端实际运动轨迹，可以看出位置内环阻抗控制器基本可以实现轨迹跟踪；同时图 4 和图 5 分别表示运动过程中期望轨迹与实际运动轨迹的误差，阻抗控制器最大误差 x 方向达到 0.0075m，y 方向达到 0.024m，位置内环阻抗控制器最大误差在 0.0015 左右，而后误差逐渐趋于稳定。 140 145 ） m （ y 150 图 3 机械臂末端位置图 4 机械臂 x 方向误差 Fig. 3 Trajectory of the manipulator Fig. 4 Manipulator error of X direction - 5 -

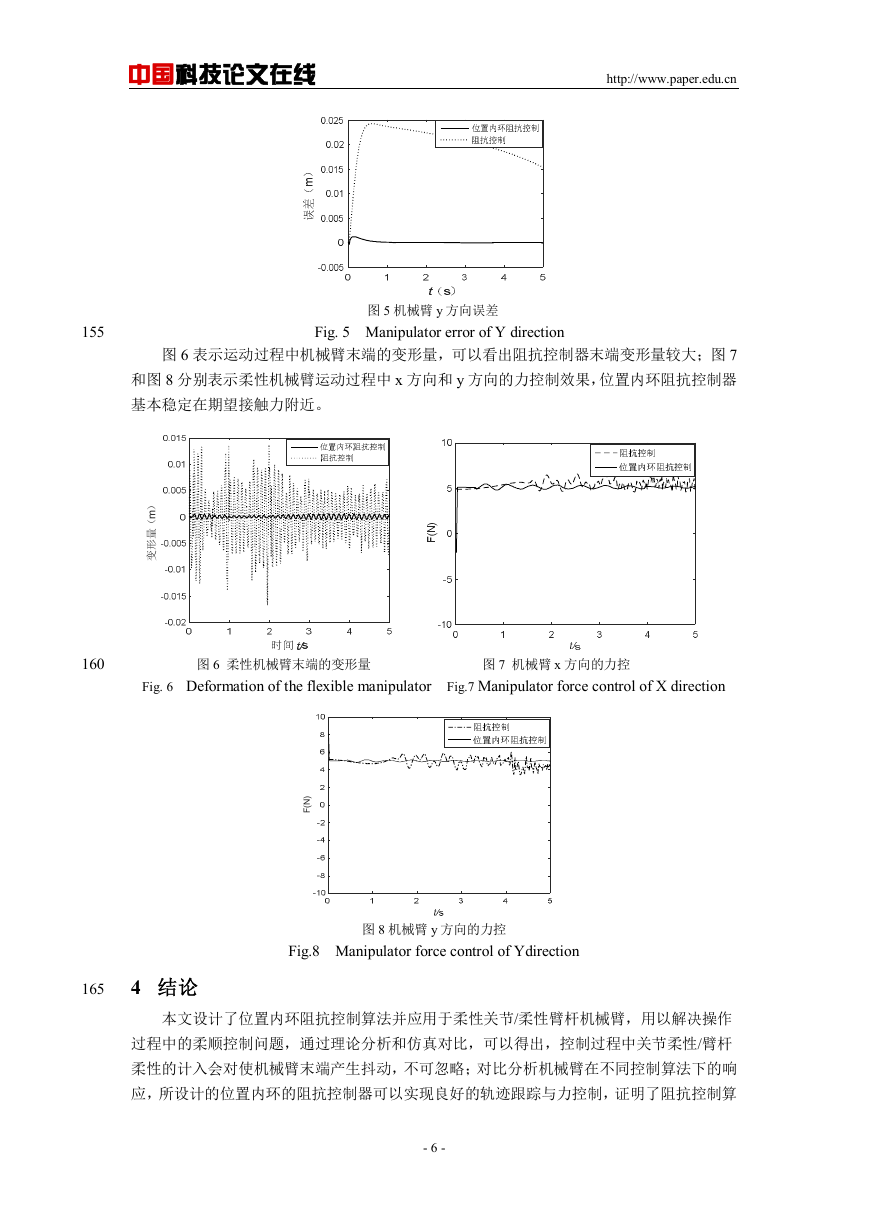
中国科技论文在线 http://www.paper.edu.cn 155 图 5 机械臂 y 方向误差 Fig. 5 Manipulator error of Y direction 图 6 表示运动过程中机械臂末端的变形量，可以看出阻抗控制器末端变形量较大；图 7 和图 8 分别表示柔性机械臂运动过程中 x 方向和 y 方向的力控制效果，位置内环阻抗控制器基本稳定在期望接触力附近。） m （量形变 160 图 6 柔性机械臂末端的变形量图 7 机械臂 x 方向的力控 Fig. 6 Deformation of the flexible manipulator Fig.7 Manipulator force control of X direction ) N ( F 图 8 机械臂 y 方向的力控 Fig.8 Manipulator force control of Ydirection 165 4 结论本文设计了位置内环阻抗控制算法并应用于柔性关节/柔性臂杆机械臂，用以解决操作过程中的柔顺控制问题，通过理论分析和仿真对比，可以得出，控制过程中关节柔性/臂杆柔性的计入会对使机械臂末端产生抖动，不可忽略；对比分析机械臂在不同控制算法下的响应，所设计的位置内环的阻抗控制器可以实现良好的轨迹跟踪与力控制，证明了阻抗控制算 - 6 -

中国科技论文在线 http://www.paper.edu.cn 170 法的可行性与有效性。 [参考文献] (References) 175 180 185 [1] Hogan N. Impedance control - An approach to manipulation. I - Theory. II - Implementation. III - Applications[J]. Journal of Dynamic Systems Measurement & Control, 1985, 107:1-24. [2] 金英连, 王斌锐, 方水光. 未知环境下柔性二连杆机械臂的自适应阻抗控制[J]. 中国机械工程, 2014(17)：2351-2355. [3] 危清清, 刘志全, 王耀兵,等. 柔性机械臂辅助空间站舱段对接阻抗控制[J]. 中国空间科学技术, 2014(6):57-64. [4] 徐国政, 宋爱国, 李会军. 基于模糊逻辑的上肢康复机器人阻抗控制实验研究[J]. 机器人, 2010, 32(6):792-798. [5] Zarafshan P, Moosavian S A A. Control of a space robot with flexible members[C]// IEEE International Conference on Robotics & Automation. IEEE, 2011:2211-2216. [6] Jiang Z H. Impedance Control of Flexible Robot Arms with Parametric Uncertainties[J]. Journal of Intelligent & Robotic Systems, 2005, 42(2):113-133. [7] Spong M W. Modeling and Control of Elastic Joint Robots[J]. Journal of Dynamic Systems Measurement & Control, 1987, 109(4):310-319. [8] Readman M C, Belanger P R. Analysis and control of a flexible joint robot[C]// Decision and Control, 1990., Proceedings of the 29th IEEE Conference on. 1991:2551-2559 vol.4. [9] 杨振. 基于阻抗控制的机器人柔顺性控制方法研究[D]. 东南大学, 2005. - 7 -

分享到：

赞收藏

资料库

具有关节柔性/臂杆柔性机械臂的位置内环阻抗控制.pdf

相关推荐

开发技术

热门标签

最新资料