2 　　电 　子 　测 　量 　技 　术 　　EL ECTRONIC M EASUREM EN T TEC HNOLO GY 研究与设计 第 31 卷 第 9 期 2008 年 9 月 　 基于 SRT 和 Restoring 算法的双精度浮点除法器设计 孙 　一 　张 　鑫 　王 　波 　冯 　为 　金 　西 (中国科学技术大学物理系微电子学教研室 　合肥 　230026) 摘 　要 : 提出了一种基于 SR T 迭代算法的除法器的改进方法 ,采用 Restoring 和 SR T 算法来互补共同完成双精度浮 点除法器的设计 ,当被除数的位数很大时采用改进过的 Restoring 算法来完成除法运算 ,并通过倒数查找表把 Restoring 和 SR T 运算结果统一起来 ; 在 SR T 运算中应用了 On fly 飞速转换算法 , 查找表模块采用 Quine McCluskey 化简方法使用高度简化的与或逻辑代替大量的比较器来实现 。上述做法有效提高了除法器的整体运算速 度 ,使得当被除数前十位有“1”的位时运算时间减少了 22. 22 %。 关键词 : SR T 算法 ; Restoring 算法 ; 查找表 ; 倒数 中图分类号 : TP332. 2 　　文献标识码 : A the Division floating point double precision based on SRT and Restoring algorithm Sun Yi 　Zhang Xin 　Wang Bo 　Feng Wei 　Jin Xi ( Instit ute of Microelect ronics Depart ment of Physics , USTC , Hefei 230026) Abstract : The improvement of the divider unit which is based on the SR T algorithm is p resented , the Restoring algorithm and the SR T algorithm is used to finish the design of division floating point double precision unit together , when the dividend has the p roperty of long bit ,the divider unit is operated by the Restoring algorithm which has been improved ,and the result is combined with SR T algorithm by recip rocal look fly conversion is concluded in SR T iteration unit , based on the Quine in combinational logic instead of lot s of multiplexers. All of above effectively increase the speed of divider unit ,when the front ten bit s of dividend has the“1”bit the latency of operation has reduce by 22. 22 %. Keywords : SR T ; Restoring ; SEL ; reciprocal McCluskey simplification SEL module also implement up table ; And the On the 0 　引 　　言 在语音通信和图像处理等领域中对 CPU 的计算精度 和速度提出了很高的要求 ,在双精度浮点数协处理器中除 法器因为采用迭代算法对处理器整体性能有较大的影响 , 对于包含 56 位尾数的双精度浮点数来说采用基为 4 的 SR T 算法完成整个运算需要 26 个时钟周期 。文献 [ 1 3 ] 给出了基于 SR T 算法的除法器的设计 ,文献[ 4 ]介绍了基 于 Restoring 算法的除法器设计 ,其中文献[ 1 ]把除法和开 方运算结合起来使得功耗能够降低 35 %左右 。本文通过 对 SR T 算法和 Restoring 算法的研究提出了基于 SR T 除 法器的改进方案 ,进一步提高了除法器的运算速度 ,使得 当被除数的前十位有值“1”时只需要 10 个时钟周期就可 以完成除法运算 ,在 SR T 算法查找表的硬件设计中使用基 本组合逻辑来代替大量比较器 ,减少查找表的时间延迟 , 在系统设计中采用自顶向下的设计方法 ,利用多种 EDA 工具对设计进行设计优化 ,完成对设计的仿真测试及验证 ·05· 综合。 1 　算法描述 IEEE754 标准定义了 32 位单精度和 64 位双精度浮点 数两种格式 ,双精度浮点数包含了 1 位符号位 ,11 位指数 位和 52 位尾数 3 个字段 。规格化的浮点数具有形式 : ±0. 1bbb. . . b ×2 ±E 有效位的第一位总是“1”,并且不需要存储于有效数 字段中 ,定义的浮点数尾数范围在 0. 5 到 1 之间 ,52 位的 双精度浮点数尾数加上在最高位前的 3 位隐含位和在最 低位后的 1 位保护位构成 56 位的二进制数位 。 实现 迭 代 型 除 法 器 的 算 法 主 要 有 3 种 算 法 : Restoring 和 SR T 算法 , SR T 算法是 Non Restoring ,Non - Restoring 算法的扩展 ,算法基数越大收敛速度越快 ,基 为 4 的 SR T 算法广泛应用于各种微处理器中。 1. 1 　预处理 SR T 算法要求被除数要比除数小 ,被除数 A 运算前要 

　　　　　　　　孙一 等 :基于 SR T 和 Restoring 算法的双精度浮点除法器设计 第 9 期 进行右移一位的操作 ,另外为了把 SR T 算法和 Restoring 算法结果统一起来 ,假如被除数为 A[ 51 :0 ] ,除数为 B[ 51 : 0 ] ,则 : Qsrt = 0. 01 A [51 ] A [ 50 ] . . . A [1 ] A [0 ] 0. 1B [51 ] B [50 ] . . . B [ 1 ] B [0 ] = 0. 01 0. 1B [51 ] B [50 ] . . . B [ 1 ] B [0 ] + 0. 00 A [51 ] A [50 ] . . . A [1 ] A [ 0 ] 0. 1B [51 ] B [50 ] . . . B [1 ] B [ 0 ] = 1 1B [ 51 ] . B [50 ] . . . B [1 ] B [0 ] + 1 0. 1B [ 51 ] B [50 ] . . . B [ 1 ] B [0 ] 0. 00 A [51 ] A [ 50 ] . . . A [ 1 ] A [0 ] 1 1. B [51 ] B [50 ] . . . B [1 ] B [0 ] ×2 - 1 + 1 Qrestoring = (1) 式 (1) 把 SR T 运算的结果和 Restoring 运算结果结合 起来 ,由此也知道 Restoring 的计算公式为 : Qrestoring = 0. 1 B [51 ] B [ 50 ] . . . B [1 ] B [0 ] 0. 00 A [ 51 ] A [50 ] . . . A [1 ] A [0 ] 1B [ 51 ] B [50 ] . . . B [ 1 ] B [0 ] 0 000 A [ 51 ] A [50 ] . . . A [1 ] A [ 0 ] = (2) Restoring 算法同样要求除数要大于被除数 ,除数的最 高位前加“1”,最低位加“0”,被除数的最高位前补上两个 “0”。 求倒数时若采用迭代法求倒数将消耗 11 个时钟周 期 ,对除法运算速度的提高没有帮助 ,本文采用了查找表 的方法来设计倒数器 ,文献 [ 5 ]介绍倒数查找表的构造方 法 ,因为改进的 Restoring 算法得到的结果最多只有从低 位开始的十位的有效数字 ,前面的高位都为“0”,设计的倒 数查找表输入项位数为 11 位满足精度要求。 除法器的运算包括两种算法 : SR T 算法和 Restoring 算法 ,当被除数的前十位没有“1”的位时 , SR T 算法在 26 个时钟周期内常规完成除法运算 ; 当被除数的前十位有 “1”的位时 ,采用 Restoring 算法在 10 个时钟周期内完成 结果输出再经过倒数查表求倒数完成除法运算 。 1. 2 　SRT 算法 基为 4 的 SR T 算法能够把除法和开方运算结合起来 , 在除法运算中每一步迭代都要执行 : R[ i+1 ] = 4 R[ i] + F[ i] F[ i] = - qi+1 ×b 式中 :i = 0 ,2 , . . . ,26 ; F 为计算缓存器 , A 为被除数 , B 为 除数 , Q 为迭代商 ;初始化 R[0 ] = A - B , Q[0 ] = 1 , A 和 B 分别限制在 0. 5 至 1 的范围内 , 每次迭代产生从低位到高 位的两位商位 ; R[ i ] 是部分余数寄存器 ,当小于 0 时以补码 的形式存储 ; q[ i + 1 ] 是通过查找表得到的商位 ,即满足 : qi+1 = S EL ( dδ,γ) 式中 : dδ 是除数的近似值 ,具体做法是取除数权重为 - 2 , - 3 , - 4 的位 , γ是 R [ i ] 的前 8 位数 , qi+1 的商数集为 { - 2 , - 1 ,0 ,1 ,2} , dδ 和γ作为查找表的输入端和 SEL 函 数比较得到 qi+1 的值 ,查找表输出冗余表示 qi+1 的值。 1. 3 　Restoring 算法 Restoring 算法称为恢复余数算法 ,在传统的除法器中 应用比较广泛 ,每次迭代产生一位商数字 ,恢复余数算法 每一步都要执行 : R[ i+1 ] = 2 R[ i] - B 式中 : R 为部分余数 , B 为除数 ,当相减的结果为负时需要 进行恢复余数的加法运算 ,并把余数恢复成上一次迭代的 数值 ,商位为 0 ;当相减的结果为正时则商位为 1 。设计中将 { R , A} 组成的缓存器在每次迭代时向左移 1 位 , A 初始为 被除数 ,余数缓存器 R 与除数 B 相减 ,若差值为负则把 { R , A} 最低位设为 0 ,否则为 1 ;同时把 B 加回 R 恢复上一次迭 代时 R 的值 。A 和 B 的位长为 56 位 , R 的位长为 57 位 ,当迭 代运算完成后{ R , A} 中的 R[55 :0 ] 为余数 , A 就是除法运 算输出的商 。 对于 本 双 精 度 浮 点 数 除 法 器 来 说 被 除 数 为 “1 B [51 ] B [50 ] …B [1 ] B [0 ]0”, 除 数 为“00 A [51 ] A [50 ] …A [1 ] A [0 ]”, 即把被除数和除数的位置颠倒了过来进行 除法运算 ,再通过倒数器输出最终结果 。 Restoring 算法的缺点是收敛速度较低 ,而且每次迭代 完成后若除数比部分余数大则还要进行加法运算恢复部 分余数的数值 ,完成 56 位的除法运算需要 56 个时钟周期 , 应用于除法器设计之前要对其进行改进。 1. 4 　算法改进 当除数 B 的数值很大时 ,商前面的位数都是“0”,通过 判断除数前面的首“1”的位置预先对 { R , A} 进行相应的移 位操作 ,从而减少迭代时间。例如 B [ 52 ]是首“1”的位 ,那 么除数前面有 B [ 55 :53 ] ,即有 3 位的“0”位 ,缓存器 { R , A} 就可以直接共同向左移位 (56 - 3) 位 ,即表明不用进行 迭代计 算 就 可 以 直 接 得 到 Q [ 55 : 3 ] 为“0 ”, 再 通 过 Restoring 迭代运算得到 Q[2 :0 ] 的值就完成 Q 的结果 输出。 在 R TL 级设计中统一让除数和“1111111111000 … 000”进行按位与运算来判断除数的首“1”位是否是在前十 位之内 ,假如结果为否 ,用 SR T 算法进行常规运算 ,反之则 把{R ,A}向左移位 46 位 ,即确定了商位的前 46 位为 0 ,然 后进入 Restoring 模块进行运算 。 2 　结构化设计 数据在进入除法器的迭代单元之前完成预处理的工 作 ,主要的功能模块是倒数查找表 ,在 ASIC 设计阶段通过 ROM 或者 PL A 来实现 ,在保证计算精度的情况下平衡输 入和输出的位数 ,使得硬件资源消耗达到最小。倒数查找 表的输入项为 11 位 ,输出项为 46 位 ,综合得到 2048 ×46 的 ROM ;当精度要求不高的场合可以把倒数查找表的输 入项减为 9 位 ,输出项为 30 位 ,综合得到 512 ×30 的 ROM 实现。查找表的时间延迟相当于逻辑门的时间延迟 ,存储 单元的数值通过 system 或者 C 语言初级建模得到 。 ·15· 

　第 31 卷 电 　子 　测 　量 　技 　术 除法器迭代单元分成 3 个设计模块 ,选择模块 ,恢复 余数运算模块和 SR T 迭代模块 , 选择模块完成除数与 “1111111111000 …000”的按位与操作 ,控制选择哪种算法 来完成除法运算 ;采用自顶向下的设计方法来完成初级建 模和设计 ,将复杂的迭代运算划分为简单且容易控制的模 块 ,使得在早期能够发现结构设计上的错误 ,同时也减少 了逻辑仿真的工作量 。 2. 1 　Restoring 迭代 图 1 是 Restoring 恢复余数算法的迭代实现电路图 , 包括 3 个主要组成部分 : res_div 迭代运算单元 ,移位器和 迭代控制器 。clk 和 itr_en 信号直接控制迭代控制器 ;res_ div 由移位器和加法器组成 ,负责生成每一步迭代的输出 商 ;移位器完成{ R ,A}向左移位 46 位 ;迭代控制器控制恢 复余数 迭 代 运 算 。整 个 迭 代 模 块 在 EP1C20F 搭 建 的 FP GA 仿真环境中消耗 415 个逻辑元件数 ,在138. 27 M Hz 的时钟频率下时间延迟为 11. 282 ns 。 图 1 　div_res 模块实现电路图 2. 2 　SRT 迭代 图 2 是 SR T 算法的迭代实现电路图 ,迭代模块完成 R 的累加 ,计数器计数和输出迭代的控制使能信号给上一层 模块 ,包括 SEL ,F GEN 和 Q GEN 3 个模块 ;顶层模块完成 信号 的 迭 代 返 回 和 结 果 最 终 输 出 。模 块 在 Cyclone EP1C20F 搭建的 FP GA 仿真环境中消耗 1 108 个逻辑元 件数 ,在时钟频率 70. 26 M Hz 下时间延迟为 17. 37 ns 。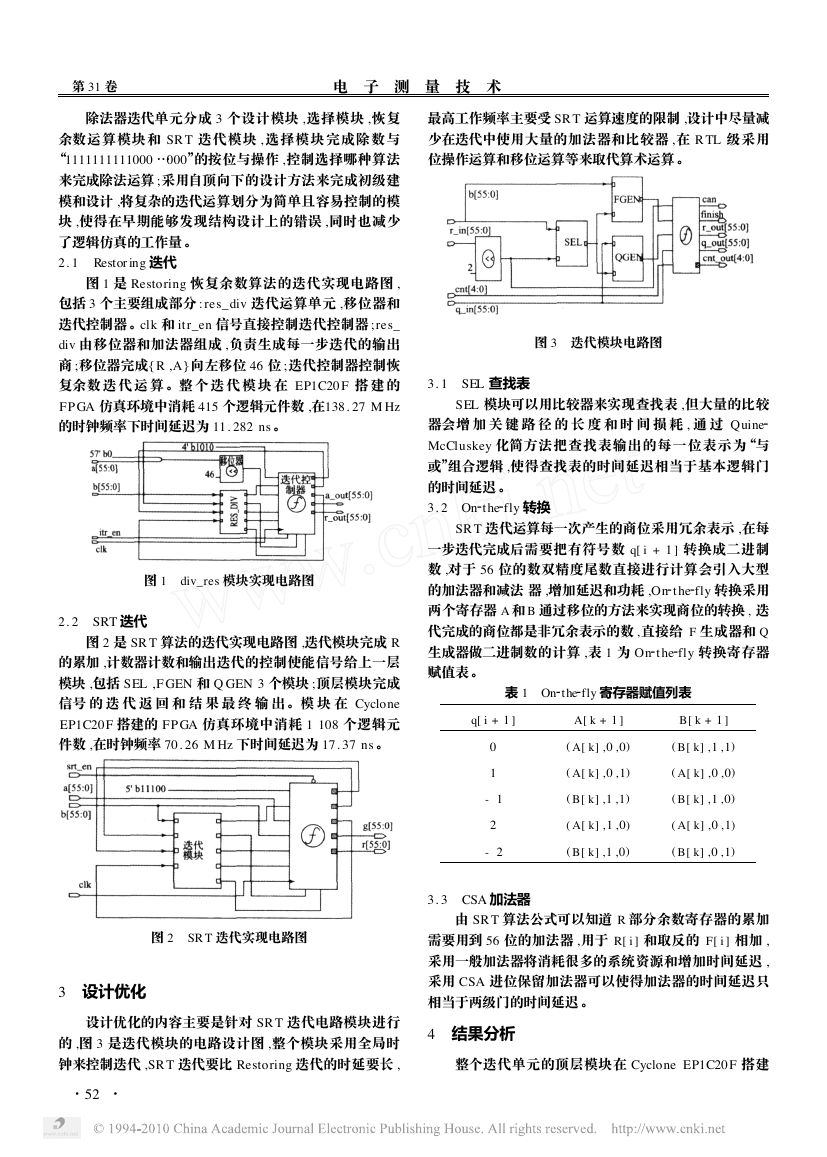 图 2 　SR T 迭代实现电路图 3 　设计优化 设计优化的内容主要是针对 SR T 迭代电路模块进行 的 ,图 3 是迭代模块的电路设计图 ,整个模块采用全局时 钟来控制迭代 ,SR T 迭代要比 Restoring 迭代的时延要长 , ·25· 最高工作频率主要受 SR T 运算速度的限制 ,设计中尽量减 少在迭代中使用大量的加法器和比较器 ,在 R TL 级采用 位操作运算和移位运算等来取代算术运算。 图 3 　迭代模块电路图 3. 1 　SEL 查找表 SEL 模块可以用比较器来实现查找表 ,但大量的比较 器会增 加 关 键 路 径 的 长 度 和 时 间 损 耗 , 通 过 Quine McCluskey 化简方法把查找表输出的每一位表示为“与 或”组合逻辑 ,使得查找表的时间延迟相当于基本逻辑门 的时间延迟 。 3. 2 　On fly 转换 the SR T 迭代运算每一次产生的商位采用冗余表示 ,在每 一步迭代完成后需要把有符号数 q[ i + 1 ] 转换成二进制 数 ,对于 56 位的数双精度尾数直接进行计算会引入大型 的加法器和减法 器 ,增加延迟和功耗 ,On fly 转换采用 两个寄存器 A 和 B 通过移位的方法来实现商位的转换 , 迭 代完成的商位都是非冗余表示的数 ,直接给 F 生成器和 Q 生成器做二进制数的计算 ,表 1 为 On fly 转换寄存器 赋值表 。 t he t he 表 1 　On the fly 寄存器赋值列表 q[ i + 1 ] A [ k + 1 ] B [ k + 1 ] 0 1 - 1 2 - 2 ( A [ k ] ,0 ,0) ( B [ k ] ,1 ,1) ( A [ k ] ,0 ,1) ( A [ k ] ,0 ,0) ( B [ k ] ,1 ,1) ( B [ k ] ,1 ,0) ( A [ k ] ,1 ,0) ( A [ k ] ,0 ,1) ( B [ k ] ,1 ,0) ( B [ k ] ,0 ,1) 3. 3 　CSA 加法器 由 SR T 算法公式可以知道 R 部分余数寄存器的累加 需要用到 56 位的加法器 ,用于 R[ i ] 和取反的 F[ i ] 相加 , 采用一般加法器将消耗很多的系统资源和增加时间延迟 , 采用 CSA 进位保留加法器可以使得加法器的时间延迟只 相当于两级门的时间延迟 。 4 　结果分析 整个迭代单元的顶层模块在 Cyclone EP1C20F 搭建 

2 2 2 　　　　　　　　孙一 等 :基于 SR T 和 Restoring 算法的双精度浮点除法器设计 第 9 期 的 FP GA 仿真环境中消耗 1 314 个逻辑元件 ,运算最高时 钟频率为 69. 89 M Hz ,模块延迟时间为 18. 274 ns 。采用 改进 Restoring 算法和 SR T 算法完成的除法器比单纯 SR T 算法完成的除法器要多消耗 18. 6 %的系统门数 ,当除 数前十位的位数有“1”时完成除法运算只需要 10 个时钟 周期 ,运算速度提高了 64. 29 %。 在 Cyclone EP1C20F 搭建的 FP GA 仿真环境中仿真 和测试得到图 4 和图 5 所示的时序图 。当除数的前十位没 有“1”的位 ,基于 SR T 算法经过 540 ns 得到结果 ;当除数 的前十位有“1”的位 ,基于 Restoring 算法经过 420 ns 得到 结果 ,运算时间减少了 22. 22 %。 5 　结 　　论 当被除数的前十位有“1”时 ,采用改进后的 Restoring 恢复余数算法代替 SR T 算法来完成运算 ,在 10 个时钟周 期后可以得到输出结果 ,并且通过组合逻辑表示 SEL ,On fly 转换冗余表示部分商和 CSA 加法器[ 8 ] 加速运算等 t he 方法对 SR T 算法的设计优化 ,提高系统最高工作频率 ,进 一步提高除法器的运算速度 ;在倒数查找表设计上采用 C 语言建模的方法预先得到每一个存储数值 ,在系统设计方 法上采用自顶向下的设计方法 ,加快了设计思想到硬件实 现的转化 ,通过大量的仿真测试来验证设计的正确性 ,并 进一步转化为 ASIC 综合 。 参 考 文 献 [ 1 ] 　 NANNARELL I A , L AN G T. low 4 Combined Division and Square Root [ C ]. IEEE International Conference on Comp uter Design ( ICCD’ 99) ,1999 (10) :236 Power Radix 242. [ 2 ] 　 HARRIS D L , OB ERMAN S F , HOROWIR TZ M A. SR T Division Architectures and Implementations [ C ]. Proceedings 13th IEEE Sympo sium , 1997 : 18 25. [ 3 ] 　 ERCEGOVAC M D , L AN G T. Radix 4 square root without initial PL A [J ]. IEEE Trans on Computers , 1990 ,39 (8) : 1016 1024. [4 ] 　 张昆藏. 计算机组织与结构 - 性能设计[ M ]. 北京 :电 子工业出版社 ,2001. [5 ] 　 李蓉 ,于伦正 ,时晨. 浮点倒数查找表的构造[J ]. 微电 子学与计算机 ,2007 ,24 (7) : 23 26. [ 6 ] 　 KORN ERU P P. Digit Selection for SR T Division and Square Root [ J ]. IEEE Transactions on comp uter , 2005 ,54 (3) :294 303. [ 7 ] 　 林灶生 ,刘绍汉. Verilog FP GA 芯片设计 [ M ]. 北京 : 北京航空航天大学出版社 ,2006. [ 8 ] 　 吕虹 ,徐慜 ,刘雨兰. 高性能 CMOS 全加器设计 [J ]. 电子测量与仪器学报 ,2006 ,20 (5) : 85 88. 作 者 简 介 孙一 ,男 ,1985 年 1 月出生 ,硕士研究 生 ,主要研究方向为浮点数协处理器设计 。 E mail :sunkai @mail. ustc. edu. cn 张鑫 ,男 ,1983 年 5 月出生 ,河南鹿邑 人 ,中国科技大学微电子学与固体电子学 专业硕士研究生 ,主要研究方向为微电子 学与固体电子学 、SoC 芯片设计。 E mail :xinz @mail. ustc. edu. cn 冯为 ,女 ,1985 年出生 ,硕士研究生 ,主要研究方向为 VL SI 设计等。 E mail : Fengwei @mail. ustc. edu. cn ·35·