利用ADS进行功放以及预失真（DPD）的设计.pdf-资料库

lvyetian-2896076-4744300845225649229.pdf-第1页.png

第1页 / 共16页

lvyetian-2896076-4744300845225649229.pdf-第2页.png

第2页 / 共16页

lvyetian-2896076-4744300845225649229.pdf-第3页.png

第3页 / 共16页

lvyetian-2896076-4744300845225649229.pdf-第4页.png

第4页 / 共16页

lvyetian-2896076-4744300845225649229.pdf-第5页.png

第5页 / 共16页

lvyetian-2896076-4744300845225649229.pdf-第6页.png

第6页 / 共16页

lvyetian-2896076-4744300845225649229.pdf-第7页.png

第7页 / 共16页

lvyetian-2896076-4744300845225649229.pdf-第8页.png

第8页 / 共16页

Seminar: Gain Without Pain November 2000 RF Predistortion of Power Amplifiers Shawn Stapleton Agilent Technologies 1400 Fountaingrove Parkway Santa Rosa, CA 95403 1

Abstract With the advent of linear modulation methods, linearization of power amplifiers has become an important technology. The adaptive work function predistorter is an approach to optimizing out-of-band intermodulation performance. This technique can adapt to changes in the power amplifier’s characteristics, including effects such as temperature changes, channel switching, power supply variation, and transistor degradation. The technique can also handle larger bandwidths than current DSP-based digital predistorters. Biography Dr. Shawn P. Stapleton has 17 years of experience in the design of RF and microwave circuits and systems. He is presently professor of electrical engineering at Simon Fraser University as well as a consultant for Agilent EEsof. He has developed GaAs MMIC components, including mixers, amplifiers, frequency dividers and oscillators. His most recent work includes digital signal processing, mobile communications and RF/microwave systems. 2

Agenda & Topics RF Predistortion of Power Amplifiers Introduction to Adaptive RF Predistortion Key Features: RF Predistortion Techniques & Concepts RF Predistortion Design Example Conclusion 3 This section of the workshop provides an introduction to predistortion. We will cover key features, technologies, and performance issues. Approaches to solving some of the design challenges will also be presented. An adaptive work function based predistorter is demonstrated using the Agilent Advanced Design System. Additional reference information is also available. 3

Technology Overview Linearization approaches: FeedForward Linearization – Based on inherently wideband technology Digital Predistortion – Limited Bandwidth (DSP implementation) Cartesian Feedback – Stability considerations limit bandwidth and accuracy LINC – Sensitive to component drift and has a high level of complexity Dynamic Biasing – Limited ACI suppression RF-Based Predistortion – Limited accuracy of function model – Implemented at RF with low complexity – Adaptation is required 4 Of the various linearization techniques that have been developed, predistortion is the most commonly used. The concept behind predistortion calls for the insertion of a nonlinear module between the input signal and the power amplifier. The nonlinear module generates IM distortion that is in anti-phase with the IM distortion produced by the power amplifier, thereby reducing out-of-band emissions. The RF-based predistorter has two distinct advantages over other approaches. First, the correction is applied before the power amplifier where insertion loss is less critical. Second, the correction architecture has a moderate bandwidth. Digital predistortion technique are more complex, but provide better IM distortion suppression. However, bandwidths are low due to limited DSP computational rates. Cartesian feedback are relatively less complex and offers reasonable IM distortion suppression, but stability considerations limit the bandwidth to a few hundred KHz. The LINC technique converts the input signal into two constant envelope signals that are amplified by Class C amplifiers, and then combined, before transmission. Consequently, they are very sensitive to component drift. Dynamic biasing is similar to predistortion, however the work function operates on the power amplifier’s operating bias. Feedforward linearization is the only strategy that simultaneously offers wide bandwidth and good IM distortion suppression. The price for this performance is higher complexity. Automatic adaptation is essential to maintain performance. 4

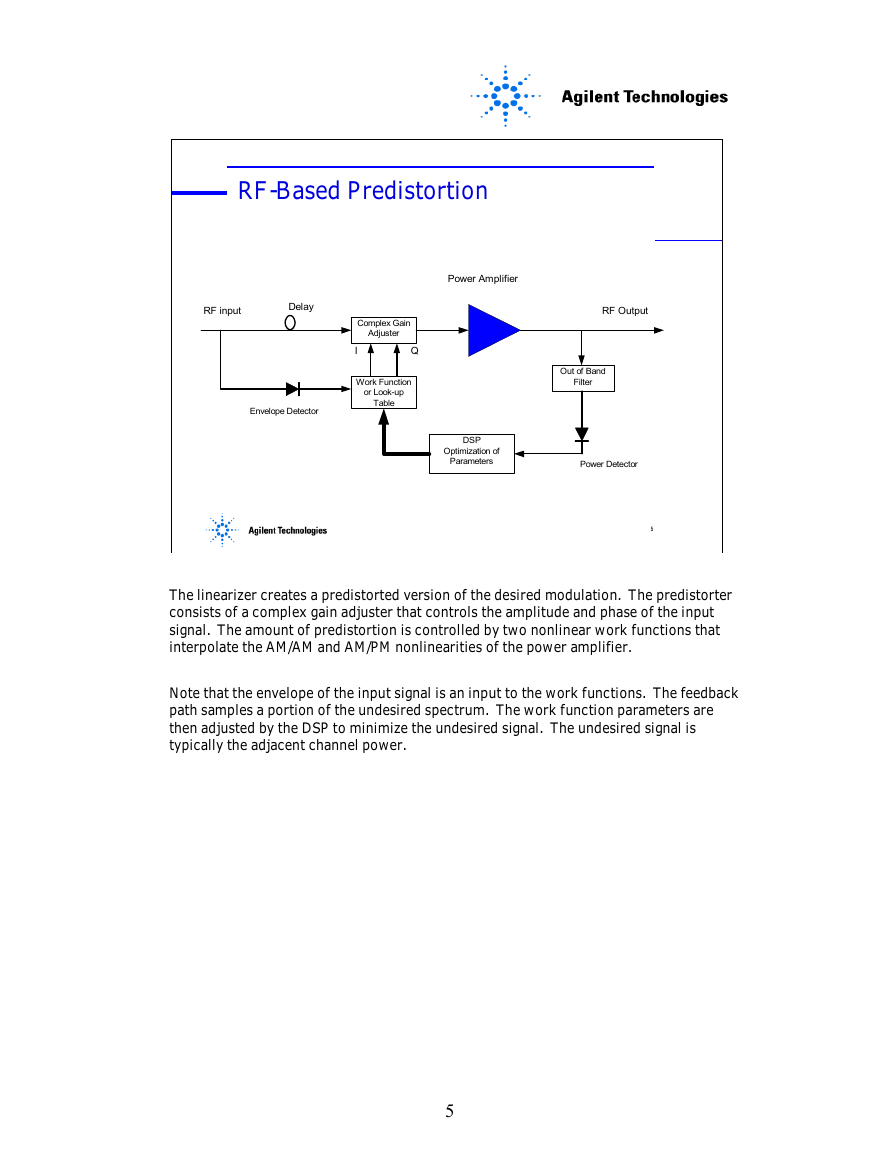
RF-Based Predistortion Power Amplifier RF input Delay Complex Gain Adjuster I Q Work Function or Look-up Table Envelope Detector DSP Optimization of Parameters RF Output Out of Band Filter Power Detector 5 The linearizer creates a predistorted version of the desired modulation. The predistorter consists of a complex gain adjuster that controls the amplitude and phase of the input signal. The amount of predistortion is controlled by two nonlinear work functions that interpolate the AM/AM and AM/PM nonlinearities of the power amplifier. Note that the envelope of the input signal is an input to the work functions. The feedback path samples a portion of the undesired spectrum. The work function parameters are then adjusted by the DSP to minimize the undesired signal. The undesired signal is typically the adjacent channel power. 5

Spectrum at the Nodes RF input Delay Complex Gain Adjuster I Q Power Amplifier RF Output Work Function or Look-up Table Envelope Detector DSP Optimization of Parameters Out of Band Filter Power Detector 6 Given a two-tone input signal, we can observe the spectral response at various nodes in the RF predistorter. The function of the envelope detector is to extract the amplitude modulation of the input RF signal. The delay line in the upper branch compensates for the time delay added as the envelope passes through the work function. The complex gain adjuster, once optimized, provides the inverse nonlinear characteristics to those of the power amplifier. Thus, we can observe the spectral growth from the predistorter at the input node of the power amplifier. Ideally the IM products will be equal in amplitude, but anti-phase the IM products created as the two tones pass through the power amplifier. The out-of-band filter samples the adjacent power interference (ACPI). The function of the DSP is to slowly adapt the work function parameters so that the ACPI is minimized. 6

Design Techniques RF-Based Predistortion Generic RF predistortion techniques – Work function (I.e. polynomial, exponential) – Look-up table – Analog nonlinearity (I.e. Diodes) Generic adaptation techniques... – ACI power minimization – Gradient evaluation 7 In the mid-’80s and early ’90s, many patents were filed covering adaptive predistortion. These patents encompass two general adaptation methods—adaptation based on power minimization and adaptation based on gradient signals. The control scheme for power-minimization adaptation is based on trying to adjust the complex gain adjuster to minimize the measured power of the error signal in the out-of- band frequency. Once the optimum parameters have been achieved, deliberate perturbations are required to continuously update the coefficients, which reduces the effects of IM distortion suppression. Adaptation based on the use of gradient signals requires a continuous computation to estimate the gradient of a three-dimensional power surface. The surface for the RF predistorter circuit is the difference between the input signal and the scaled output signal. This power is minimized when the error signal is completely suppressed. Since the gradient is continually updated, no deliberate misadjustment is required. There are three distinct RF predistortion techniques. The work function-based approach utilizes a low-order polynomial to fit the AM/AM and AM/PM characteristics of the power amplifier. The look-up table technique fits the power amplifier’s characteristics more accurately. However, it requires a more sophisticated adaptation technique. The analog nonlinearity technique uses diodes to generate IM distortion. This IM distorition is then phased and attenuated to make it anti-phase with the distortion created by the power amplifier. 7

Rectangular Work Function Predistorter Power Amplifier RF input Delay Complex Gain Adjuster I Q Work Function or Look-up Table Envelope Detector DSP Optimization of Parameters I Q ) + j F F22((ρρρρρρρρ)) Rectangular Gain Function Rectangular Gain Function F(F(ρρρρρρρρ) = F) = F11((ρρρρρρρρ) + j FF11((ρρρρρρρρ) = (1+G FF22((ρρρρρρρρ) = (1+P ρρρρρρρρ is squared envelope is squared envelope Delay ) = (1+G1 1 ρρρρρρρρ+G+G2 2 ρρρρρρρρ22)) ) = (1+P1 1 ρρρρρρρρ+P+P2 2 ρρρρρρρρ22)) ρρρρρρρρ LPF Envelope Detector From DSP G1 G2 P1 P2 RF Output Out of Band Filter Power Detector 8 The rectangular work function implementation requires the use of a complex gain adjuster, which has in-phase and quadrature controls. The work function consists of a simple second- order polynomial expressed in terms of the squared envelope. When this function is multiplied by the input signal in the complex gain adjuster, a fifth-order polynomial is produced which is expressed in terms of the signal envelope. There are four parameters that are slowly adapted by the DSP or microprocessor, with the ultimate goal of minimizing the adjacent channel power interference. 8

资料库

利用ADS进行功放以及预失真（DPD）的设计.pdf

相关推荐

课程资源

热门标签

最新资料