遗传算法与蚂蚁算法的融合.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.69M 资料格式：pdf 举报版权申诉

zh1234qwer-7300147-9168c45124d4e0bdecf76d517c24ef79.pdf-第1页.png

第1页 / 共13页

zh1234qwer-7300147-9168c45124d4e0bdecf76d517c24ef79.pdf-第2页.png

第2页 / 共13页

zh1234qwer-7300147-9168c45124d4e0bdecf76d517c24ef79.pdf-第3页.png

第3页 / 共13页

zh1234qwer-7300147-9168c45124d4e0bdecf76d517c24ef79.pdf-第4页.png

第4页 / 共13页

zh1234qwer-7300147-9168c45124d4e0bdecf76d517c24ef79.pdf-第5页.png

第5页 / 共13页

zh1234qwer-7300147-9168c45124d4e0bdecf76d517c24ef79.pdf-第6页.png

第6页 / 共13页

zh1234qwer-7300147-9168c45124d4e0bdecf76d517c24ef79.pdf-第7页.png

第7页 / 共13页

zh1234qwer-7300147-9168c45124d4e0bdecf76d517c24ef79.pdf-第8页.png

第8页 / 共13页

文本预览

第 40 卷第 2003 年 9 期 9 月计算机研究与发展 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! ! J OURNAL OF COMPUTER RESEARCH AND DEVELOP MENT Vol. 40 ， No. 9 Sep. 2003 遗传算法与蚂蚁算法的融合丁建立陈增强袁著祉（南开大学信息技术科学学院天津（ jianli di ng !yahoo. com. cn ）） 300071 摘要遗传算法具有快速随机的全局搜索能力，但对于系统中的反馈信息利用却无能为力，当求解到一定范围时往往做大量无为的冗余迭代，求精确解效率低 . 局搜索能力 . 但初期信息素匮乏，求解速度慢 . 蚂蚁算法是通过信息素的累积和更新收敛于最优路径上，具有分布式并行全算法是将遗传算法与蚂蚁算法融合，采用遗传算法生成信息素分布，利用蚂蚁算法求精确解，优势互补 . 仿真表明取得了非常好的效果 . 关键词遗传算法；蚂蚁算法；融合；中图法分类号 TP301 ； TP18 On t he Co mbi nati on of genetic al gorit h m and ant al gorit h m Dl NG Ji an- Li （， CHEN Zeng- Gi ang ， and YUAN Zhu- Zhi College of Information technology and science Nankai unioersity ，， tianJin 300071 ） abstract Genetic al gorit h m has t he abilit y of doi ng a global searchi ng guickl y and st ochasticall y. But it ’ can t make use of enough syste m out put i nf or mati on. lt has t o do a large redundancy repeat f or t he result when sol vi ng t o certai n scope. So t he efficiency t o sol ve precisi on results is reduced. Ant al gorit h m con- verges on t he opti mizati on pat h t hrough i nf or mati on phero mone accu mulati on and rene wal. lt has t he abili- t y of parallel processi ng and global searchi ng. The speed at which t he ant al gorit h m gi ves t he sol uti on is because t here is little i nf or mati on phero mone on t he pat h earl y. The al gorit h mi n t his paper is based slow ， it adopts genetic al gorit h mt o gi ve i nf or- ， it makes use of t he ant al gorit h mt o gi ve t he precisi on of t he sol u- ， it develops enough advantage of t he t wo al gorit h ms. The si mulati on results show t hat very on t he co mbi nati on of genetic al gorit h m and ant al gorit h m. First mati on phero mone t o distri bute. Second ti on. Fi nall y nice eff ects are obtai ned. ， Key words genetic al gorit h m ； ant al gorit h m ； co mbi nati on 引言 1 遗传算法是由美国密执安大学的教授于 1975 John Holland 年首先提出的一类仿生型优化算法 . 它是以达尔文的生物进化论“适者生存、优胜劣汰” 启发式智能化方法近年来愈来愈引起了众多学和孟德尔的遗传变异理论“生物遗传进化主要在染诸如神经网络、模拟退火、禁忌搜色体上，子代是父代遗传基因在染色体上的有序排者的关注和兴趣 . 索、遗传算法、蚂蚁算法、计算等，它们毫无争 DNA 议地成为解决组合爆炸及类问题的锐利工具 . 然而，面对各种问题的特殊性和复杂性，每一种算法 NP 都表现其自身的优势和缺陷，都会面临时间性能和优化性能的双重挑战［ 1 ］ . " 关； # 列”为基础，模拟生物界进化过程 . 其优点是：具有大范围全局搜索的能力，与问题领域无搜索从群体出发，具有潜在的并行性；可进行多值比较，鲁棒性强；收稿日期： 2002- 10- 23 ；修回日期： 2003- 06- 12 基金项目：国家自然科学基金（ 60174021 ）；天津自然科学基金重点项目（ 013800711 ）；河南科技攻关项目（ 0124140141 ）

计算机研究与发展年 2003 搜索使用评价函数启发，过程简单；使用概率机制进行迭代，具有随机性；最短路径 . 特别地，当蚂蚁巢穴与食物源之间出现障碍物时，蚂蚁不仅可以绕过障碍物，而且通过蚁群 2531 ＠＠具有可扩展性，容易与其他算法结合 . ＠其缺点是：对于系统中的反馈信息利用不信息素轨迹在不同路径上的变化，经过一段时间的正反馈，最终收敛到最短路径上［ 6 ， 7 ］ . 够［ 2 ］，当求解到一定范围时往往做大量无为的冗余蚂蚁圈模型 2. 2 迭代，求精确解效率低 . 蚂蚁算法（ ant al gorit h m AA ，）是近年来刚刚诞生的随机优化方法，它是一种源于大自然的新的仿生类算法 . 它是意大利学者等最早提 M. Dori go 出［ 3 ， 4 ］的，蚂蚁算法主要是通过蚂蚁群体之间的信息传递而达到寻优的目的，最初又称蚁群优化方法（ ant colony opti mizati on 用了人工蚂蚁的概念，因此亦称蚂蚁系统（ ACO ，由于模拟仿真中使） . ant SyS- ， te m AS 其优点是：） . 其原理是一种正反馈机制或称增强型学习系统，它通过信息素的不断更新达到最终收敛于最它是一种通用型随机优化方法，但人工蚂蚁决不是对实际蚂蚁的一种简单模拟，它融进了人类优路径上；的智能； d i ＠＠它是一种全局优化的方法，不仅可用于求解单目标优化问题，而且可用于求解多目标优化问题 . 其缺点是：初期信息素匮乏，求解速度慢［ 5 ］ . 遗传算法生成信息素分布，利用蚂蚁算法求精确解，优势互补，期望获得优化性能和时间性能的双赢 . 蚂蚁算法的优化机理及模型描述蚂蚁算法的优化机理 2 2. 1 蚂蚁圈模型是全局优化较好的蚂蚁算法，假如路径（ i ， j 在路径（ i ， j 时刻信息素轨迹强度为）在 I k ）上留下的单位长度轨迹信息素数量，蚂蚁 Tij ），则轨迹强度的更，轨迹的持久性＠Tk ij 新方程［ 6 ， 8 ］为（ P 0 P 1 ） · （ I = P 只蚂蚁在本次循环中所走的路径（） + ＠Tk I ij ） . Kij ，其中是一个常数［ 5 ，］ 6 . ）的能见度，一般取为 @ ）的长度，路径可见度的（ Tij 设 Zk 的长度，则如果设 Tij ／ dij ，这里 1 相对重要性 I + 1 为第 k （＠Tk = @ I ij 为边路径（ i 为路径（ i ）／ Zk ， j ， j dij （ B B 0 ），路径轨迹的相对重要性（ O O 时刻的转移概 0 率为）， U （ 1k I ij 为可行顶点集，蚂蚁 k ，）可定义［ 6 8 在 I ］如下），则（ 1k I ij ［（ I Tij ［ l U ， 0 （］B ）］O［（ I Til Tij ）］O［ Til ，］B ， j U 其他 . ）算法 2. 3 MMAS max- mi n ant syste m 算法是比利时学者 MMAS 出的［ 8 ］，它对基本蚂蚁算法（ Tho maS St utzle 点改进［ 9 ）进行了 AS 3 提］： d 为最大值 Tmax ； i 一圈中只有最短路径的蚂蚁才进＠行信息素修改增加，这与蚂蚁圈模型调整方法 AS 相似；为了避免算法过早收敛非全局最优解，将各路经的信息素浓度限制在［，］之间，超出这个范围的值被强制设为从实验结果看， MMAS 算法在防止算法过早停滞及有效性方面 Tmi n Tmax 或者 Tmax. Tmi n 它是一种分布式的优化方法，不仅适合目前（ 1k I ij ） = 的串行计算机，而且适合未来的并行计算机；本文算法是将遗传算法与蚂蚁算法的融合，采用为了更加充分地进行寻优，各路径信息素初值设蚂蚁有能力在没有任何提示下找到从其巢穴到对算法有较大的改进 . AS 食物源的最短路径，并且能随环境的变化而变化，适应性地搜索新的路径，产生新的选择 . 其根本原因是蚂蚁在寻找食物源时，能在其走过的路上释放一遗传算法与蚂蚁算法的融合（ GAAA ） 3 种特殊的分泌物———信息素（，随着时间算法的设计思想及总体框架 phero mone 3. 1 GAAA 的推移该物质会逐渐挥发），后来的蚂蚁选择该路径遗传算法与蚂蚁算法的融合（的概率与当时这条路径上该物质的强度成正比 . 一定路径上通过的蚂蚁越来越多时，其留下的信息当素轨迹也越来越多，后来蚂蚁选择该路径的概率也， genetic algorit h m- ），其基本思想是汲取两种算法的 ant algorit h m 优点，克服各自的缺陷，优势互补 . GAAA 在时间效率上优于蚂蚁算法，在求精解效率上优于遗传算法，是时间效越高，从而更增加了该路径的信息素强度 . 而强度大的信息素会吸引更多的蚂蚁，从而形成一种正反率和求解效率都比较好的一种新的启发式方法 . 其基本思路是算法前过程采用遗传算法，充分馈机制 . 通过这种正反馈机制，蚂蚁最终可以发现利用遗传算法的快速性、随机性、全局收敛性，其结

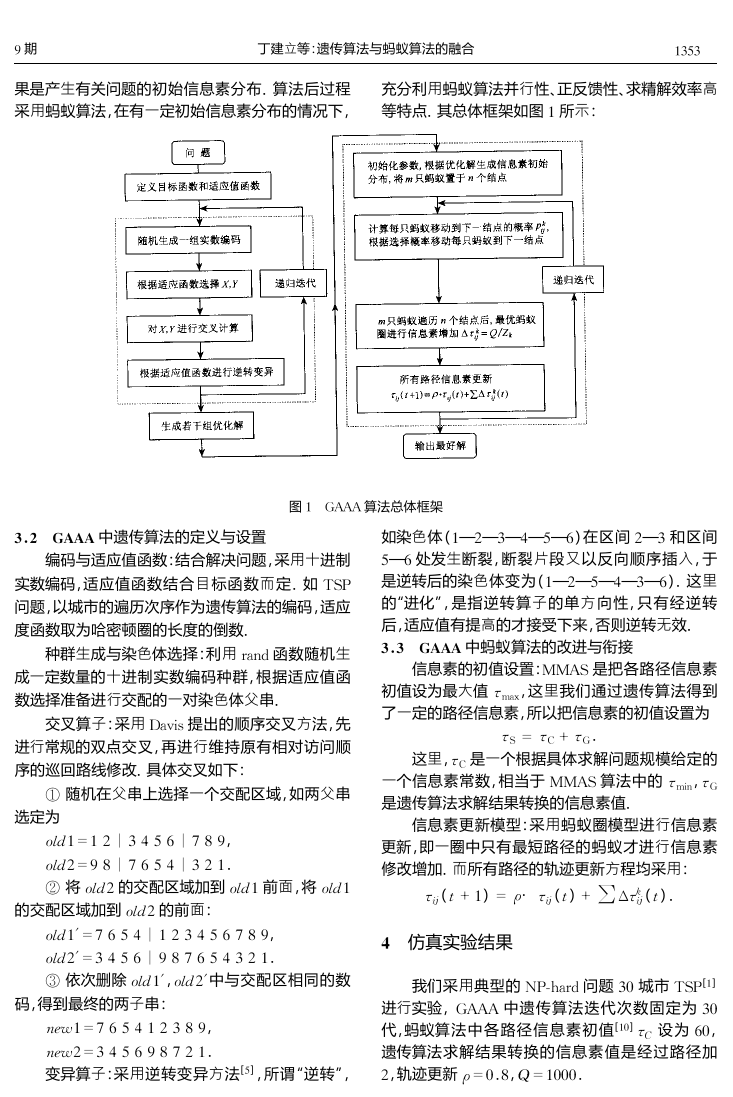
期 9 丁建立等：遗传算法与蚂蚁算法的融合 3531 果是产生有关问题的初始信息素分布 . 采用蚂蚁算法，在有一定初始信息素分布的情况下，算法后过程充分利用蚂蚁算法并行性、正反馈性、求精解效率高等特点 . 其总体框架如图所示： 1 图 1 GAAA 算法总体框架 3.2 GAAA 中遗传算法的定义与设置编码与适应值函数：结合解决问题，采用十进制实数编码，适应值函数结合目标函数而定 . TSP 问题，以城市的遍历次序作为遗传算法的编码，适应如度函数取为哈密顿圈的长度的倒数 . 种群生成与染色体选择：利用成一定数量的十进制实数编码种群，根据适应值函数选择准备进行交配的一对染色体父串 . 交叉算子：采用提出的顺序交叉方法，先 Davis 进行常规的双点交叉，再进行维持原有相对访问顺序的巡回路线修改 . 具体交叉如下：随机在父串上选择一个交配区域，如两父串 ! 选定为 Old1 = 1 2 !3 4 5 6 !7 8 9 ， Old2 = 9 8 !7 6 5 4 !3 2 1. 的交配区域加到将 " Old2 的交配区域加到的前面： Old2 Old1 = 7 6 5 4 !1 2 3 4 5 6 7 8 9 Old2 = 3 4 5 6 !9 8 7 6 5 4 3 2 1. ， Old1 前面，将 Old1 依次删除 Old1 ， Old2 # 码，得到最终的两子串：中与交配区相同的数 new1 = 7 6 5 4 1 2 3 8 9 ， new2 = 3 4 5 6 9 8 7 2 1. 变异算子：采用逆转变异方法［ 5 ］，所谓“逆转”，函数随机生 3.3 GAAA rand — 4 — 2 — 6 — 5 — 6 — 3 ）在区间如染色体（ 1 和区间处发生断裂，断裂片段又以反向顺序插入，于 5 是逆转后的染色体变为（这里 1 的“进化”，是指逆转算子的单方向性，只有经逆转后，适应值有提高的才接受下来，否则逆转无效 . — 5 — 2 — 4 — 3 — 3 — 6 ） . 2 中蚂蚁算法的改进与衔接信息素的初值设置：初值设为最大值了一定的路径信息素，所以把信息素的初值设置为 !max 是把各路径信息素，这里我们通过遗传算法得到 MMAS !S = !C + !G. 是一个根据具体求解问题规模给定的这里， !C 一个信息素常数，相当于是遗传算法求解结果转换的信息素值 . MMAS 算法中的 !mi n ， !G 信息素更新模型：采用蚂蚁圈模型进行信息素更新，即一圈中只有最短路径的蚂蚁才进行信息素修改增加 . （而所有路径的轨迹更新方程均采用：） · （ r !ij （） + "$!k r ij ） . !ij r + 1 = " 仿真实验结果 4 我们采用典型的［ 1 TSP 中遗传算法迭代次数固定为 NP- har d 城市问题 30 GAAA 进行实验，代，蚂蚁算法中各路径信息素初值［遗传算法求解结果转换的信息素值是经过路径加］ !C 设为 30 60 10 ］，，轨迹更新 "= 0. 8 2 ， @ = 1000.

计算机研究与发展年 2003 最优解，和目前得到的最好解一致 . 图 4 ! 图 7 找到的解与最优解非常接近，是其 4531 表反映 1 GAAA 算法优化解数据逼近过程，图算法中经过遗传算法求解结果形象说明了 2 在信息素初值设置的表现 . GAAA 是一个逐步收敛的过程，从均值和分布来看，其求精在遗传阶段采用随机产生的种群，因而有效地避免从中可以看出本文算法他算法容易陷入局部最优的几个值，本文算法因为确解的精度非常高 . 图 3 是应用 GAAA 算法得到的了陷入局部最优 . 过程 GAAA 初始随机生成的一组优化解遗传算法后生成的一组优化解蚂蚁算法后生成的一组优化解表 ! "### 算法优化解数据逼近过程优化解分布最大值最小值平均值 1309 1333 1181 1119 1271 1256 1401 1216 1275 1293 1046 1385 1302 1263 1309 1347 1448 1227 1288 1283 1500 1046 1298 .8 1181 1289 1500 1387 1460 1364 1206 1217 1441 1303 961 918 993 888 938 939 922 838 834 868 924 892 816 901 941 987 926 916 871 918 987 817 912 .3 949 947 908 912 926 975 825 919 989 817 436 430 431 439 426 437 433 429 434 439 426 438 424 426 425 446 449 426 424 443 452 424 433 .7 434 427 452 436 426 425 448 431 440 430 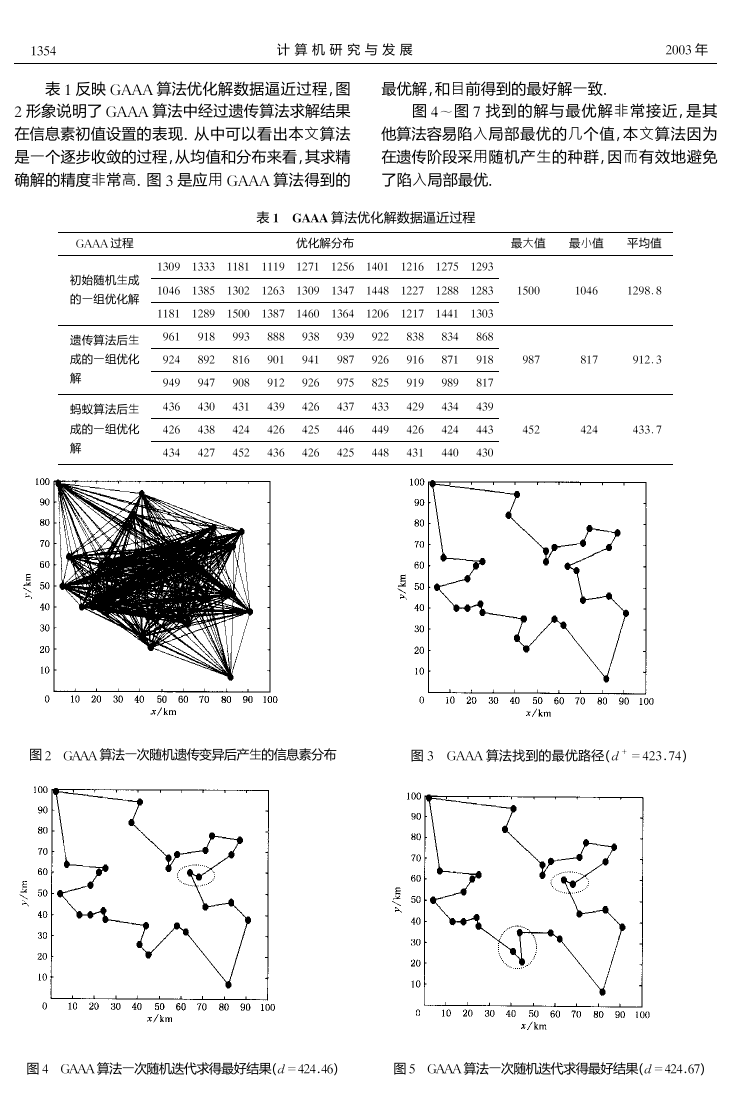图 2 GAAA 算法一次随机遗传变异后产生的信息素分布图 3 GAAA 算法找到的最优路径（ !+ = 423. 74 ）图 4 GAAA 算法一次随机迭代求得最好结果（ !=424. 46 ）图 5 GAAA 算法一次随机迭代求得最好结果（ !=424. 67 ）

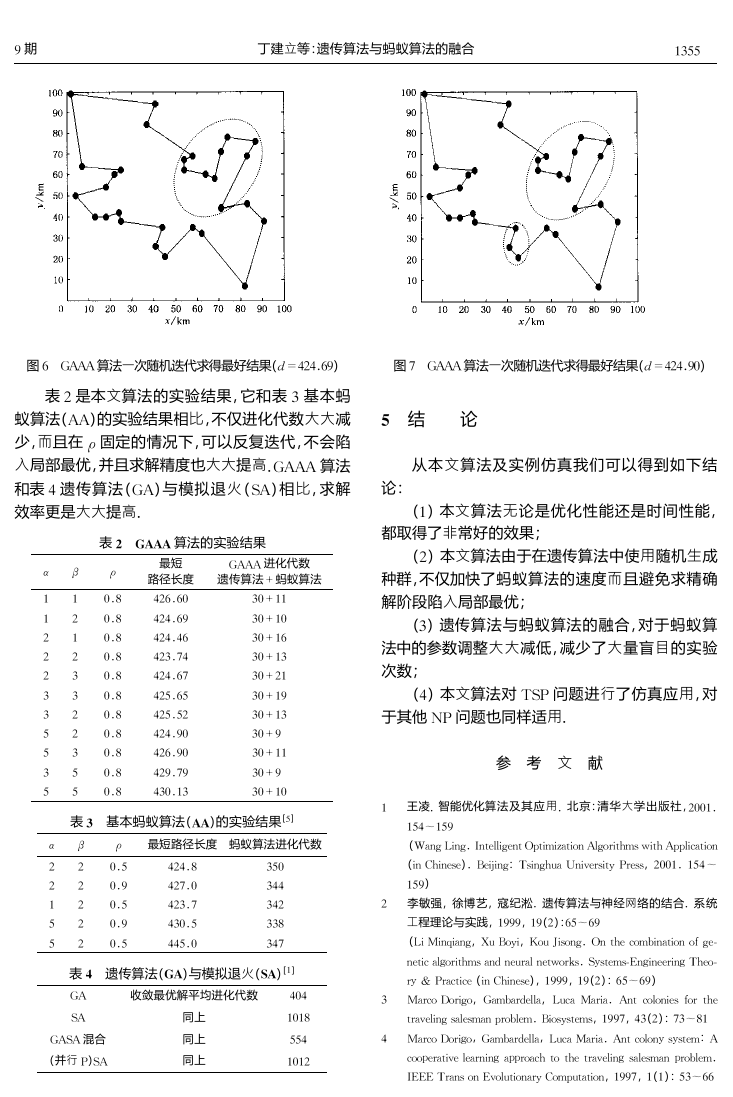
期 9 丁建立等：遗传算法与蚂蚁算法的融合 5531 图 6 GAAA 算法一次随机迭代求得最好结果（ !=424. 69 ）图 7 GAAA 算法一次随机迭代求得最好结果（ !=424. 90 ）入局部最优，并且求解精度也大大提高算法从本文算法及实例仿真我们可以得到如下结表是本文算法的实验结果，它和表基本蚂 3 ）的实验结果相比，不仅进化代数大大减固定的情况下，可以反复迭代，不会陷 2 蚁算法（ AA 少，而且在 ! 结论 5 和表遗传算法（）与模拟退火（）相比，求解论： . GAAA SA 4 GA 效率更是大大提高 . 表 2 GAAA 算法的实验结果 " # ! 路径长度最短 GAAA 遗传算法进化代数蚂蚁算法 + 1 1 2 2 2 3 3 5 5 3 5 1 2 1 2 3 3 2 2 3 5 5 表 3 0. 8 0. 8 0. 8 0. 8 0. 8 0. 8 0. 8 0. 8 0. 8 0. 8 0. 8 426. 60 424. 69 424. 46 423. 74 424. 67 425. 65 425. 52 424. 90 426. 90 429. 79 430. 13 30 + 11 30 + 10 30 + 16 30 + 13 30 + 21 30 + 19 30 + 13 30 + 9 30 + 11 30 + 9 30 + 10 基本蚂蚁算法（）的实验结果［ 5 AA " # ! 2 2 1 5 5 2 2 2 2 2 0. 5 0. 9 0. 5 0. 9 0. 5 最短路径长度蚂蚁算法进化代数 424. 8 427. 0 423. 7 430. 5 445. 0 350 344 342 338 347 表 4 GA SA GASA （并行混合） SA P 遗传算法（）与模拟退火（ GA ）［ 1 ］ SA 收敛最优解平均进化代数同上同上同上 404 1018 554 1012 （ 1 （ 2 （ 3 ）本文算法无论是优化性能还是时间性能，都取得了非常好的效果；）本文算法由于在遗传算法中使用随机生成种群，不仅加快了蚂蚁算法的速度而且避免求精确解阶段陷入局部最优；）遗传算法与蚂蚁算法的融合，对于蚂蚁算法中的参数调整大大减低，减少了大量盲目的实验次数；（ 4 于其他）本文算法对问题进行了仿真应用，对 TSP 问题也同样适用 . NP 参考文献］ 1 王凌 . 智能优化算法及其应用 . 北京：清华大学出版社， 2001. 154 !159 （ Wang Li ng. I ntelli gent Opti mizati on Algorit h ms wit h Applicati on （ i n Chi nese ） . Beiji ng ： Tsi nghua Uni versit y Press ， 2001. 154 ! ） 159 李敏强，徐博艺，寇纪淞 . ，工程理论与实践， 1999 （ 2 19 ）： 65 !69 遗传算法与神经网络的结合 . 系统（ Li Mi nCiang ， Xu Boyi ， Kou jisong. On t he co mbi nati on of ge- netic al gorit h ms and neural net wor ks. Syste ms- Engi neeri ng Theo- ry & Practice Marco Dori go （）， i n Chi nese ， Ga mbardella 1999 ，，（ 2 19 ）： 65 !69 ） Luca Maria. Ant colonies f or t he traveli ng sales man proble m. Bi osyste ms ， 1997 ，（ 2 43 ）： 73 !81 Marco Dori go ， Ga mbardella ， Luca Maria. Ant colony syste m ： A cooperati ve learni ng approach to t he traveli ng sales man proble m. I EEE Trans on Evol uti onary Co mputati on ， 1997 （， 1 1 ）： 53 !66 2 3 4

&!%# 计算机研究与发展年 (’’% ! 吴庆洪，张纪会，徐心和 " 具有变异特征的蚁群算法 " 计算机 #’ H3<9+@C3.D3:: 7.D<6>S6>-@"7B3<3::6:-=B:6=6.838-1.1?3.8 ，研究与发展， #$$$ ，（ %& #’ ）： #()’!#()! （ *+,-./01./ 203./4-0+- 5+5-.06"7.3.891:1.;3:/1<-80= ，， >-80=+838-1.?638+<6@"41+<.3:1?A1=B+86

遗传算法与蚂蚁算法的融合作者：丁建立，陈增强，袁著祉作者单位：刊名：英文刊名：年，卷(期)：南开大学信息技术科学学院,天津,300071 计算机研究与发展 JOURNAL OF COMPUTER RESEARCH AND DEVELOPMENT 2003,40(9) 207次被引用次数：参考文献(10条) 1.王凌智能优化算法及其应用 2001 2.李敏强;徐博艺;寇纪淞遗传算法与神经网络的结合[期刊论文]-系统工程理论与实践 1999(02) 3.Marco Dorigo;Gambardella;Luca Maria Ant colonies for the traveling salesman problem 1997(02) 4.Marco Dorigo;Gambardella;Luca Maria Ant colony system: A cooperative learning approach to the traveling salesman problem[外文期刊] 1997(01) 5.吴庆洪;张纪会;徐心和具有变异特征的蚁群算法[期刊论文]-计算机研究与发展 1999(10) 6.Marco Dorigo;Eric Bonabeau;Theraulaz Guy Ant algorithms and stigmergy[外文期刊] 2000(08) 7.张素兵;刘泽民基于蚂蚁算法的时延受限分布式多播路由研究[期刊论文]-通信学报 2001(03) 8.Thomas Stutzle;Holger H Hoos MAX-MIN ant system[外文期刊] 2000(08) 9.吴斌;史忠植一种基于蚁群算法的TSP问题分段求解算法[期刊论文]-计算机学报 2001(12) 10.Marcus Randall;Andrew Lewis A parallel implementation of ant colony optimization[外文期刊] 2002(09) 本文读者也读过(2条) 1. 李敏强.徐博艺.寇纪淞.Li Minqiang.Xu Boyi.Kou Jisong 遗传算法与神经网络的结合[期刊论文]-系统工程理论与实践1999,19(2) 2. 张铃.张钹.ZHANG Ling.ZHANG Bo 遗传算法机理的研究[期刊论文]-软件学报2000,11(7) 引证文献(207条) 1.刘先刚.廖述剑网格任务调度算法的研究[期刊论文]-机械工程与自动化 2011(1) 2.刘彬求解车间作业调度问题的一种新型蚁群算法[期刊论文]-中国科技纵横 2010(12) 3.王剑雄.王玉兰.张志宏.王海东.闫常丽在多约束非线性优化问题上蚂蚁与遗传算法融合方法的研究[期刊论文]- 河北建筑工程学院学报 2009(3) 4.刘胜辉.王丽红求解车间作业调度问题的混合遗传算法[期刊论文]-计算机工程与应用 2008(29) 5.武艳.曲波量子遗传算法在人脸图像分割中的应用[期刊论文]-中国西部科技 2008(30) 6.王丽红.刘胜辉求解Job-Shop调度问题的改进蚁群算法[期刊论文]-信息技术 2008(1) 7.周鹏带有单亲遗传特征的蚁群算法[期刊论文]-计算机工程与设计 2007(9) 8.许梁海.倪志伟.赖大荣混合型蚁群算法及其应用研究[期刊论文]-电脑知识与技术（学术交流） 2005(8) 9.王浩.曹仲伟基于遗传蚁群算法的Qos路由约束问题的研究[期刊论文]-湖北工业大学学报 2011(2) 10.高大利改进蚁群算法在物流配送路径问题中的应用[期刊论文]-泉州师范学院学报 2010(2) 11.陆楠.李晓林基于遗传-蚂蚁算法的关联规则挖掘方法[期刊论文]-信息技术 2010(3) 12.王喆蚁群算法及其在火力分配问题中的应用[期刊论文]-火力与指挥控制 2009(11) 13.高大利基于改进蚁群算法的物流配送路径问题研究[期刊论文]-泉州师范学院学报 2009(2)

14.夏谦.雷勇.叶小勇遗传算法在AGV全局路径优化中的应用[期刊论文]-四川大学学报（自然科学版） 2008(5) 15.王雅芳遗传算法结合蚁群算法电力系统故障浅析[期刊论文]-系统仿真技术 2008(1) 16.沈国强.覃征一种新的多维关联规则挖掘算法[期刊论文]-小型微型计算机系统 2006(2) 17.翁国栋蚁群算法与遗传算法对TSP的一种融合[期刊论文]-福建电脑 2006(2) 18.黄少荣群智能算法的混合策略研究[期刊论文]-长江大学学报（自然版） 2011(12) 19.洪波.李正光改进蚁群遗传算法在大规模车间调度中的研究[期刊论文]-福建电脑 2010(1) 20.王会颖.耿家礼基于蚁群算法求解最大团问题[期刊论文]-计算机应用与软件 2010(10) 21.张建民.恰汗·合孜尔.高大利基于改进蚁群算法的物流配送路径问题研究[期刊论文]-计算机工程与科学 2010(7) 22.刘朝华.张英杰.李小花.吴建辉双态免疫优势蚁群算法及其在TSP中的应用研究[期刊论文]-小型微型计算机系统 2010(5) 23.张玮.李承祖基于遗传蚁群算法的高含水油田集输系统的运行优化[期刊论文]-石油规划设计 2010(2) 24.田宝勇.周应强一种新的决策树组合优化算法[期刊论文]-辽宁大学学报（自然科学版） 2010(1) 25.李春梅.杨新存蚂蚁算法及其应用[期刊论文]-科技风 2010(2) 26.宋存利.薛倩混合蚁群遗传算法在车间作业调度的应用研究[期刊论文]-科学技术与工程 2009(11) 27.傅调平.陈建华.李刚强基于遗传蚁群算法的舰艇编队防空火力分配[期刊论文]-计算机仿真 2009(6) 28.黄立君.许永花遗传算法和蚁群算法融合求解TSP[期刊论文]-东北农业大学学报 2008(4) 29.黄立君 GAAA算法在乳品企业原奶车辆运输路径中的应用[期刊论文]-农机化研究 2008(1) 30.马琳面向安全服务重组多目标优化的粒子群遗传算法[期刊论文]-中南林业科技大学学报 2007(5) 31.邢伟仓库空调系统的节能优化试验研究[期刊论文]-农机化研究 2007(11) 32.苏淼.钱海.王煦法基于免疫记忆的蚁群算法[期刊论文]-计算机仿真 2007(10) 33.郭立伟.杨荃冷连轧负荷分配优化方法[期刊论文]-钢铁研究学报 2007(12) 34.王一冰可拓蚁群算法[学位论文]硕士 2007 35.王会颖.贾瑞玉.刘慧婷.李建洋一种求解TSP问题的分段交换蚁群算法[期刊论文]-计算机工程与应用 2006(35) 36.田涛.周娅.黄桂敏 P2P应用系统设计平台研究[期刊论文]-网络安全技术与应用 2006(2) 37.赵晴.贾晓萌.高蒙.李慧鹏改进蚁群算法在全局路径规划中的应用[期刊论文]-河北省科学院学报 2012(3) 38.许卫宝.王超.何宝.黄胜.周斌粒子群算法在翼型剖面优化中的应用[期刊论文]-船舶力学 2011(6) 39.李智勇.陈友文一种融入小生境技术的遗传禁忌算法[期刊论文]-湖南大学学报（自然科学版） 2010(4) 40.贾瑞玉.王会颖基于改进蚁群算法的聚类分析[期刊论文]-计算机应用与软件 2010(12) 41.王峰峰.王仁明.伍佳求解TSP问题的一种改进蚁群算法[期刊论文]-自动化技术与应用 2010(7) 42.张学琴网格环境下的任务调度研究[期刊论文]-科技信息 2009(33) 43.杨惠.李峰粒子群和蚁群融合算法的自主清洁机器人路径[期刊论文]-计算机工程与应用 2009(32) 44.张翠军.邹慧.张有华基于二次分配问题的混合蚁群算法[期刊论文]-计算机工程与应用 2008(10) 45.王树恩.史文利供应链二级分销网络的优化研究[期刊论文]-西安电子科技大学学报（社会科学版） 2007(6) 46.汪采萍.胡学钢.王会颖基于蚁群算法的多维0-1背包问题的研究[期刊论文]-计算机工程与应用 2007(30) 47.王子君.赵卫国.王利英.王江生基于人工免疫-蚁群算法的平面QoS路由模型[期刊论文]-河北工程大学学报(自然科学版) 2007(3) 48.于红斌.李孝安基于分区策略的蚂蚁算法[期刊论文]-微处理机 2007(3) 49.罗光春.李炯一种新型网格资源调度算法的研究[期刊论文]-核动力工程 2007(3)

分享到：

赞收藏

资料库

遗传算法与蚂蚁算法的融合.pdf

相关推荐

开发技术

热门标签

最新资料