logo资料库

D2D中继辅助通信的能效优化算法研究.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.82M 资料格式：pdf 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    08-20051-‰ê.pdf
    第 41 卷第 3 期 2020 年 3 月 通 信 学 报 Journal on Communications Vol.41 No.3 March 2020 D2D 中继辅助通信的能效优化算法研究 王雪 1，金涛 1，钱志鸿 1，胡良帅 1，王鑫 1,2 (1. 吉林大学通信工程学院，吉林 长春 130012；2. 吉林农业大学信息技术学院，吉林 长春 130118） 摘 要：针对蜂窝系统下 D2D 中继辅助通信的能量效率优化问题，在保证蜂窝用户与 D2D 用户服务质量的条件 下，提出了一种能效优化算法。首先，以最大化系统中总 D2D 用户能效为目标，将优化问题建模为一个混合整 数非线性规划问题。然后，将能效优化问题转化为功率控制、中继选择和信道分配 3 个子问题分别进行求解。最 后，利用 Dinkelbach 方法和拉格朗日乘子方法解决功率控制问题；利用所提出的基于 Q 学习的中继选择算法完成 中继的选择；基于功率控制和中继选择，利用匈牙利算法完成信道的分配。仿真结果表明，与现有算法相比，所 提算法可有效提高系统 D2D 用户的总能效。 关键词：D2D 通信；中继选择；功率控制；信道分配；能量效率 中图分类号：TP393 文献标识码：A doi: 10.11959/j.issn.1000−436x.2020048 Research on maximizing energy efficiency for relay-aided D2D communication WANG Xue1, JIN Tao1, QIAN Zhihong1, HU Liangshuai1, WANG Xin1,2 1. College of Communication Engineering, Jilin University, Changchun 130012, China 2. College of Information &Technology, Jilin Agricultural University, Changchun 130118, China Abstract: In order to optimize the energy efficiency for relay-aided D2D communication underlaying cellular network, an algorithm was proposed while guaranteeing the quality of service of D2D users and cellular users. Firstly, the problem was formulated as a mixed integer nonlinear fractional programming problem, with the goal of maximizing the energy ef- ficiency of all D2D users. Then, the maximizing energy efficiency problem was divided into three sub-problems, such as power allocation, relay selection and subcarrier assignment. Finally, the power allocation problem, the relay selection problem and the subcarrier assignment problem were addressed by Dinkelbach method and Lagrange multiplier method, Q-learning and Hungarian algorithm, respectively. The simulation results show that the proposed algorithm can improve the total energy efficiency of D2D users compared with existing algorithms. Key words: D2D communication, relay selection, power control, subcarrier assignment, energy efficiency 1 引言 作为 5G 的关键技术之一，D2D（device-to- device）通信技术是指通信网络中邻近设备不通过 基站而直接交换信息的技术[1]。在无线通信系统中 加入 D2D 通信技术，不仅可以提高系统频谱效率， 降低时延，还可以减轻核心网络的负载[2]。但是， 当 D2D 通信中用户间距离较远或者链路质量较差 时，需要引入中继来保证信息的可靠、有效传输。 并且，引入中继可以扩大蜂窝系统的覆盖范围[3-4]。 随着用户设备的大量增长以及终端设备电池容量 的限制，如何有效地提高能量效率，实现绿色通信， 是未来无线通信发展的关键。 现有的文献大多研究的是蜂窝通信与 D2D 直 收稿日期：2020−01−20；修回日期：2020−02−20 基金项目：国家自然科学基金资助项目（No.61771219）；吉林大学基础科研基金资助项目（No.SXGJQY2017-9, No.2017TD-19） Foundation Items: The National Natural Science Foundation of China (No.61771219), Fundamental Research Funds of Jilin Uni- versity (No.SXGJQY2017-9, No.2017TD-19)
    ·72· 通 信 学 报 第 41 卷 连通信并存场景下的能效优化问题。文献[5]通过使 用联合迭代拍卖算法，优化了包括蜂窝用户在内的 所有终端设备的能效。文献[6]考虑 D2D 通信复用 蜂窝链路下行频谱资源，在满足蜂窝用户 QoS （quality of service）的条件下，最大化系统总 D2D 链路的能量效率。文献[7]则考虑的是 D2D 通信复 用蜂窝链路上行频谱资源，基于能效构造 D2D 链 路与蜂窝链路之间的二分图，利用盖尔−沙普利算 法解决 D2D 用户与蜂窝用户之间的匹配问题。文 献[8]通过联合解决 D2D 直连通信下的功率控制和 信道分配问题，最大化系统 D2D 用户对的能效。 文献[9]将非凸形式的能效优化问题转换为凸函 数进行求解，提出了一种联合信道分配和功率控 制的两层优化算法。文献[10]在 D2D 直连通信中 加入了能量采集（EH, energy harvesting）技术，研 究了包含能量采集时隙、功率和信道分配的能效优 化问题。 在蜂窝通信与 D2D 中继通信并存场景下，可 以从模式选择、功率控制、中继选择/信道分配等多 个方面去优化能效。文献[11-12]考虑从功率控制角 度优化能效，不同的是，前者利用非线性整数规划 方法解决了单个 D2D 中继链路的能效最大化问题， 后者则利用在线学习策略从全局角度最大化系统 的能量效率。考虑功率控制和信道分配 2 个方面， 文献[13]首先最大化 D2D 中继通信的第一跳链路和 第二跳链路的能效，然后基于两跳链路的能效值， 采用匹配算法选择合适的中继，最大化系统中 D2D 链路的总能效。文献[14]假设中继具有从射频信号 中获得能量的 EH 技术功能，研究 D2D 通信中的功 率控制和中继选择问题。文献[15]提出了一种基于 能效最优的模式选择策略，在确定最优中继数量的 条件下，通过选择使用中继通信或者协同通信的方 式来优化系统的能效。文献[16]考虑了 D2D 通信的 直连、中继及协同 3 种通信方式共存的场景，通过 将优化问题拆分成联合模式选择、功率控制和信道 分配 3 个子问题分别求解，提高了系统的 D2D 链 路能效。 文献[11-16]大多只是从功率控制和中继选择， 或者功率控制和信道分配两方面考虑优化 D2D 中 继通信的能效，缺乏联合三者的研究，因此，本文 在 D2D 中继辅助通信系统中，通过联合考虑功率 控制、中继选择以及信道分配以最大化系统 D2D 用户的总能效。本文首先建模能效优化问题，并将 能效优化问题拆分为功率控制、中继选择和信道分 配 3 个子问题。然后，利用非线性整数规划及凸优 化理论解决功率控制问题，利用强化学习中的 Q 学 习算法解决中继选择问题。最后，基于功率控制和 中继选择，结合匹配理论，使用匈牙利算法求解信 道分配问题。仿真结果表示，与现有文献对比，本 文所提的算法在保证蜂窝用户和 D2D 用户的传输 速率的条件下，有效地增加 D2D 用户的能量效率。 2 系统模型及问题描述 2.1 系统模型 C D , } 假设在单小区蜂窝系统中，存在 N 对 D2D 用 户、L 个理想中继以及 K 个蜂窝用户，其中，一对 D2D 用户包含一个 D2D 发射端和一个 D2D 接收 N ， M 端。D2D 用户对的索引集合表示为 ={1,2, , } N ，D2D S D2D 发射端的索引集合表示为 ={1,2, , } N ，中继的索 接收端的索引集合表示为 ={1,2, , } L ，蜂窝用户的索引集合 R 引集合表示为 ={1,2, K 。假设 D2D 用户的发射端与 , } 表示为 ={1,2, 接收端之间由于链路质量较差，没有直连通路，只 能通过中继进行通信，且中继均采用放大转发协 议，同时每个蜂窝用户都已经预先分配了正交信 道。系统模型如图 1 所示，假设某一 D2D 用户对 ∈ 复 用 蜂 窝 用 户 c C∈ m s d m M s S d D 的上行链路频谱资源，通过中继 r R∈ 进行通信。在 D2D 中继通信第一跳链路中，中继 r 和基站的信干 噪比（SINR, signal to interference plus noise ratio） 分别为 = ( , ∈ )( , ∈ , ) SINR r 1( D ) = SINR r 1( ) BS = PG s sr + P G c cr N 0 P G cb c + PG s sb N 0 图 1 系统模型 (1) (2)
    第 3 期 王雪等：D2D 中继辅助通信的能效优化算法研究 ·73· 其中，Ps 和 Pc 分别表示 D2D 发射端和蜂窝用户的 传输功率，Gsr、Gsb、Gcr 和 Gcb 分别表示 D2D 发 射端到中继、D2D 发射端到基站、蜂窝用户到中 继和蜂窝用户到基站的信道增益，N0 表示加性高 斯白噪声。 在 D2D 中继通信第二跳链路中，D2D 接收端 d 和基站的信干噪比分别为 SINR r 2( D ) = SINR r 2( ) BS = P G r rd PG + cd c P G cb c + P G r rb N 0 N 0 (3) (4) 其中，Pr 表示中继的传输功率，Grd、Grb 和 Gcd 分 别表示中继到 D2D 接收端、中继到基站和蜂窝用 户到 D2D 接收端的信道增益。 2.2 问题描述 根据式(1)和式(3)，D2D 发射端 s 到 D2D 接收 端 d 的能效表达式为 EE s d , = Wx mr lb[1 min(SINR ,SINR )] + ) r ( 2 D (5) ) r ( 1 D ) 2 + P cir 1 ( η P P s r + 其中，xmr 表示中继选择因子，当 D2D 用户对 m 通 过中继 r 完成通信时 xmr=1，否则 xmr=0；Pcir、W 和 η 分别表示电路功率、信道带宽和功率放大系数。 本文旨在最大化整个系统的 D2D 用户对的能 效，具体表达式为 max , , , r X Y P P P c , s s.t. ∑ r R ∈ x mr ≤ 1, ∑ ∑∑ ∑ m M c C r R ∈ ∈ m M , ∈ ∀ ∈ y mc EE s d , (6) x mr ≤ 1, ∀ ∈ r R (7) y mc ∑ c C ∈ ∀ ∈ c C ∈ m M , ∀ ∈ , mc y ≤ ∈ 1, ∀ ∈ ≤ ≤ mrx ≤ {0,1}, m M m M r R ∀ ∈ ∀ ∈ ∑ 1, , m M ∈ mcy m M c C ∈ ∀ ∈ P s S∀ ∈ 0 , D max r R∀ ∈ P , 0 D max c C∀ ∈ P 0 , C ≤ ≤ max W R ≥ lb(1 SINR )r D 1( ) D min W R ≥ lb(1 SINR )r D 2( ) D min {0,1}, sP rP cP + + ≤ ≤ (8) (9) (10) (11) (12) (13) (14) (15) W 2 r [lb(1 SINR ) ( ) 1 BS + + lb(1 SINR )] + r ( ) 2 BS ≥ (16) R C min 其中，X 表示中继选择矩阵，矩阵 X 第 m 行、第 r 在计算出蜂窝用户功率最小传输功率 min =P s 列的元素是中继选择因子 xmr；Y 表示信道选择矩 阵，矩阵 Y 第 m 行、第 c 列的元素是信道复用因子 ymc，当 D2D 对 m 复用蜂窝用户 c 的信道通信时 ymc=1，否则 ymc=0；向量 和 =P 分别表示 D2D 发射端、中继和蜂窝用户 c DP 表示 D2D 发射端和中继的最 的传输功率向量； max CP 表示蜂窝用户的最大传输功率； 大传输功率； max DR 表示 D2D 通信链路必须满足的最小传输速率； min CR 表示蜂窝用户必须满足的最小传输速率。 min P ∈ ， { } r r R c CP ∈ { } c s SP ∈ { } s =P r 约束式(7)和式(8)保证一个中继只能服务一个 D2D 用户对，并且一个 D2D 用户对只能复用一个 中继。类似地，约束式(9)和式(10)保证一条信道只 能被一个 D2D 用户对复用，并且一个 D2D 用户对 只能复用一条蜂窝用户的信道。约束式(11)~式(13)分 别是 D2D 发射端、中继和蜂窝用户的传输功率限 制。约束式(14)~式(16)分别是 D2D 第一跳链路、 D2D 第二跳链路和蜂窝用户链路的传输速率限制。 由多个约束条件和变量可以看出，本文的能效 优化问题 是 一个混合 整 数非线性 规 划（MINLP, mixed integer non-linear programing）的 NP-hard 问 题，而 NP-hard 问题没有一个有效的直接求解方法。 为了求解这个优化问题，本文将其分为功率控制、 中继选择和信道分配 3 个子问题进行求解。 3 功率控制、中继选择和信道分配算法 3.1 基于 Dinkelbach 方法和拉格朗日乘子法的功 率控制算法 假设 D2D 用户对 m 通过中继 r 进行通信，并 且复用蜂窝用户 c 的信道资源，则 xmr=1 且 ymc=1， D2D 发送端 s 到接收端 d 的能效优化问题为 s.t. (17) 由式(5)可得出，D2D 发射端到接收端的能效是 关于蜂窝用户功率 Pc 的减函数，所以为了最大化 D2D 发射端到接收端的能效，功率 Pc 需要取得最 小值。根据约束式(13)、式(16)和文献[11]，得出蜂 窝用户最小传输功率为 max EE P P P , s c 式 s d , , 式 (11)~ (16) r P min c = min P G P G D rb max D max sb , ) + N ⎤ ⎦ 0 ) ( 1 2 − CR min W G cb P C max , ⎧ ⎪ ⎨ ⎪ ⎩ max( ⎡ ⎣ ⎫ ⎪ ⎬ ⎪ ⎭ (18) cP 之
    ·74· 通 信 学 报 第 41 卷 ) ) r ( 1 D SINR =SINR 后，优化式(17)中仍然有 2 个变量 Ps 和 Pr，并且式(17) 是一个分数形式，其分子不是一个确定的表达式， 不能通过已有的数学方法直接求解。在文献[11]中 r ( D 的条件，才能 已经证明，只有满足 2 得到 D2D 发射端到 D2D 接收端的最优能效值。因 r ( D 条件下，将得到的蜂窝 此，本文在 2 cP 代入式(17)所示的优化问题 用户最小传输功率 min 中，优化问题可以改写为 lb(1 + A P ⎞ ⎟ ⎠ SINR =SINR A P s 0 P cir r ( 1 D + 2 s ) ) ) + max P s W 1 1 ⎛ 0 ⎜ Bη ⎝ 0 (14)式 和式(20) s.t. P 0 D ≤ ≤ th G sr P G min cr c D P B D ⎫ P max 0 ⎬ max A ⎭ 0 B ， 0 N+ sP = = , 0 A 其 中 ， 0 P D th =min ⎧ ⎨ ⎩ (19) (20) ， N+ 0 G rd P G min c cd 为 D2D 发射端的功率上界。 式(19)是一个分数形式的非凸函数，所以利用 Dinkelbach 方法将其转换成等价的凸函数形式。首 1q 表示 D2D 发射端到接收端的能效值， 先，用变量 * 并且定义式(19)所示的最大能效为 q * 1 = max P s W lb(1 A 0 B 0 + A P s 0 ) P s + 2 P cir = + ⎞ ⎟ ⎠ 1 ⎛ ⎜ η ⎝ 1 W lb(1 A 0 B 0 + A P * s 0 ) P * s + 2 P cir + ⎞ ⎟ ⎠ 1 ⎛ ⎜ η ⎝ 1 (21) sP 是能效取最大值时 D2D 发射端的传输功 其中， * 率。由文献[17]有引理 1 成立。 1q 引理 1 当且仅当以下条件成立时得到 * ⎤ ⎥ ⎥ ⎦ ⎡ A 1 0 ⎢ Bη ⎢ ⎣ 0 max lb(1 P s A P s 0 P cir ⎞ ⎟ ⎠ W P s + − + + 1 2 ) = W lb(1 + A P * s 0 ) − q * 1 P * s + 2 P cir ⎞ ⎟ ⎠ ⎤ ⎥ ⎥ ⎦ = 0 (22) 证明 证明过程请参考文献[17]。 证毕。 由引理 1 可将优化问题式(19)从分数形式转化 为等价的减式形式，即 ⎡ A 1 ⎛ 0 ⎢ ⎜ Bη ⎢ ⎝ ⎣ 0 (14) ⎞ ⎟ ⎠ 式 和式 (20) ⎧ ⎪ W ⎨ ⎪ ⎩ max P s s.t. A P s 0 lb(1 q * 1 P s + − + 1 ) + 2 P cir ⎤ ⎥ ⎥ ⎦ ⎫ ⎪ ⎬ ⎪ ⎭ (23) q * 1 ⎛ ⎜ ⎝ ⎡ A 1 0 ⎢ Bη ⎢ ⎣ 0 ⎛ ⎜ ⎝ + 1 式(23)为一个带约束条件的凸优化问题，可使 1q 有关， 用拉格朗日乘子法求解，但是所得结果与 * 1q 的值，本文通过迭代进行计算。假设在 为了获得 * 第 n 次 迭 代 中 功 率 变 量 为 Ps(n) 以 及 能 效 值 为 q n − ，则式(23)的增广拉格朗日式为 1( sL P δθ = ( A P n W lb(1 0 1) , ) ( ) 2 P n s q n ( 1 ( )) P cir + − + − , s 1 + − 1) ⎡ A 1 ⎛ 0 ⎢ ⎜ Bη ⎢ ⎝ ⎣ 0 { ( n W lb 1 ( ) ⎞ ⎟ ⎠ A P n ( ) 0 + s ) ⎤ ⎥ ⎥ ⎦ } s ] − + − θ P D th R D min n P n ( )[ ( ) δ (24) 其中， ( )nδ 和 ( )nθ 分别是约束式(14)和式(20)的拉 格朗日算子。根据拉格朗日对偶分解，式(19)的能 效优化问题等价为 , ) δθ (25) , L P min max ( s ( , δθ 0) ≥ ( ) P s 由 KKT(Karush-Kuhn-Tucker)条件可求得 + 0 x − = N ⎫ ⎬ ⎭ (26) ˆ ( ) P n s ⎧ ⎨ ⎩ + = P G min + c cr G sr n e ( )]lb n ( ) ηδ 。拉格朗日算子 ( )nδ 和 ( )nθ W [1 η θ + q n 1) ( − + 1 x 其中，{ } max{0, } 的值可由梯度下降法迭代更新，计算式为 P ]}D + th ( , ) τ ]} + (28) 其中，τ表示拉格朗日算子的第τ次迭代，α为步 长。中继的最优功率 * ( , ) δ τ α τ ˆ s W [ θ τ α 1)={ ( , ) 1)={ ( , ) (27) A P n 0 δ τ θ τ ˆ P n s lb(1 n ( , n ( , U min + + − + − + − n n [ P * r =min (29) rP 的计算式为 ⎫ ⎧ ⎨ ⎬ ⎩ ⎭ P ,D max B 0 A 0 P * s 在功率控制问题的求解过程中包含两层迭代。 其中，外层迭代是为了求解 q1，迭代次数用 n 表示， 最大迭代次数为 Iouter，迭代误差为 1Δ ；内层迭代为 了更新拉格朗日算子δ和θ，迭代次数用τ表示， 最大迭代次数为 Iinner，迭代误差为 2Δ 。功率控制的 具体步骤如算法 1 所示。 算法 1 基于 Dinkelbach 方法和拉格朗日乘子 法的功率控制算法 W、 max 输入 Gsr、Gsb、Gcr、Gcb、Grd、Grb、Gcd、N0、 DP 、 max CP 、 min 1q 、 * 输出 * 1) ∀ ∈ DR 和 min CR rP sP 和 * m M r R ∀ ∈ for ,
    第 3 期 王雪等：D2D 中继辅助通信的能效优化算法研究 ·75· 2) 初始化：n=1、τ=0、q1(0)、 ( , )nδ τ 、 ( , )nθ τ 、 Iouter、Iinner、 1Δ 和 2Δ ，根据式(18)计算 min cP 3) 4) while n
    ·76· 通 信 学 报 第 41 卷 依照某种策略选择动作 at，随后更新 Q 值函数。当 所有的动作状态值都被频繁地执行后，Q 估计值最 终会收敛到最优 Q 值上，从而获得最优策略。 本文将中继选择的过程建模为 D2D 用户对学 习寻找最优中继的过程，分别定义 Q 学习中的智能 体，动作集合 At、状态集合 St 和奖赏函数 Rt 如 式(32)~式(34)所示。 , 2 ( = a l A t a a , 1 智能体：所有 D2D 用户对。 ) (32) 其中，al 表示选择中继 l 完成通信。在 t 时刻的动 作 at 可以是集合 At 中任一元素。 s ,EE < EE th 1 s ,EE EE 2 (33) ≥ S s d , s d , th ⎧⎪= ⎨ ⎪⎩ t , 其中，EEs,d 表示 D2D 发射端到 D2D 接收端的能效 值，可通过功率控制进行计算；EEth 表示 D2D 链路 的能效阈值。 1 EE , EE ⎧ ⎪= ⎨ tR λ ⎪−⎩ 1, s d , 其他 ≥ th EE s d , (34) 其中，λ表示放大系数。奖赏函数反映了中继选择 的好坏，若选择的中继满足 D2D 链路的最小能效 时，返回一个正值；若不满足，返回一个负值。当 每对 D2D 用户完成 Q 学习过程后，会生成对应于 中继的 Q 表，根据 Q 表，便可以选择最优中继。 具体的基于 Q 学习的中继选择过程如算法 2 所示。 算法 2 基于 Q 学习的中继选择算法 1) 对于 m M ∀ ∈ ，计算|Gm|，根据|Gm|升序排 列得到新的 D2D 用户对集合 M* t )=0 2) 找到集合 M*中第一个元素 m*，对于 m*， Q s a , 设置 ( t 由式(33)得到 m*的初始状态 st 3) while Q 值没有收敛 4) 根据 ε-贪婪算法选择动作 at 5) 计算此时 D2D 用户对的能效 EEs,d 6) 根据式(34)计算 Rt 7) 观测新的状态 st+1 8) 9) 根据式(31)计算 Q 值并更新 Q 表 10) 更新智能体的状态为 st+1 11) end while 12) 根据 Q 表计算出 m*的最佳中继 r* 13) 从 M*中删除 m*并更新|Gm|和 M* 14) for m M ∈ * \ { m } * 15) 重复步骤 2)~步骤 14) 16) end for 17) 输出中继选择矩阵 X 3.3 基于匹配理论的信道分配算法 在 3.1 节和 3.2 节中，通过功率控制和中继选 择可以得到 D2D 用户对在复用某一蜂窝用户信 道下的最大能效，本节讨论如何为每个 D2D 用户 对分配合适的信道以最大化系统总 D2D 用户的 能效。 , G V E 由于蜂窝用户集合 C 和 D2D 用户集合 M 是 2 个 互不相交的集合，因此本文构建二分图 ( ) = ， 其中二分图中顶点 V 表示蜂窝用户集合和 D2D 用 户对集合，边 E 表示为 D2D 用户对和蜂窝用户之 间的连线。在 3.1 节的功率控制中，通过约束式(16) 已经满足蜂窝用户的 QoS，所以在信道分配时，只 需要考虑如何最大化系统总 D2D 用户对的能效。 因此，设定 D2D 用户与蜂窝用户之间边的权重表 示的是该 D2D 用户复用该蜂窝用户信道时的能效 值。引入 N K× 的矩阵 T 表示权重矩阵，矩阵的行 表示 D2D 用户对，矩阵的列表示蜂窝用户。 根据以上分析，信道分配问题可以转换为最大 二部图匹配问题，并使用匈牙利算法进行求解。由 匈牙利算法计算出一个包含信道分配信息的布尔 矩阵 Y，根据矩阵 Y 便可为每个 D2D 用户分配合适 的信道。具体信道分配过程如算法 3 所示。 算法 3 基于匹配理论的信道分配算法 1) 对于 ∀ ∈ ，通过功率控制和中 m M c C ∀ ∈ , 继选择得到 N K× 的权值矩阵 T = j K 2) 使用匈牙利算法得到信道分配矩阵 Y 3) 4) 5) 6) 7) 8) 9) N i 1 to for 1 to for = if yij =1 将蜂窝用户 j 的信道分配给 D2D 用户 i end if end for end for 3.4 复杂度分析 本文所提出的能效优化算法由 3 个部分组成， 分别是基于 Dinkelbach 方法和拉格朗日乘子法的功 率控制算法、基于 Q 学习的中继选择算法和基于匹 配理论的信道分配算法。在假设 D2D 用户获得确 定辅助的中继以及复用的信道情况下，得出单一 D2D 用户能效最大时的功率分配解。之后，基于功
    第 3 期 王雪等：D2D 中继辅助通信的能效优化算法研究 ·77· 率分配的解，在假设复用信道确定的条件下，利用 Q 学习计算 D2D 用户在复用任意一条信道时的最 佳中继。基于功率控制和中继选择，计算 D2D 用 户复用每条可用信道时的能效矩阵，利用匈牙利算 法得到信道分配解。虽然本文提出的能效算法复杂 度较高，但是能在理论上获得系统总 D2D 用户的 最大能效值。 本文所提能效优化算法的复杂度取决于功率 控制、中继选择和信道分配算法。基于 Dinkelbach 方法和拉格朗日乘子法的功率控制算法复杂度为 O(IouterIinner)，考虑 N 个 D2D 用户对，K 个蜂窝用户 以及每个 D2D 用户对可复用的最大中继数 L，则功 率控制算法的复杂度为 O(MNRIouterIinner)。基于 Q 学 习的中继选择算法的复杂度取决于 Q 学习中状态 集合数|St|和动作集合数|At|，所以中继选择算法的复 杂度为 O(|St||At|)。基于匹配理论的信道分配算法复杂 度为 O(K3)，其中 K 为蜂窝用户数。综上所述，本文 提出的联合功率控制、中继选择和信道分配的能效优 化算法的复杂度为 O(MNRIouterIinner+ |St||At|+K3)。 4 仿真结果及分析 本文使用 Matlab 仿真工具对算法进行仿真，重 复执行 1 000 次蒙特卡洛实验，然后对结果取平均 值。每一次算法执行过程中，中继、蜂窝用户和 D2D 用户均随机分布在系统中。假设系统内 D2D 与蜂窝链路的阴影衰落均服从均值为 0、标准差分 别为 12 dB 与 10 dB 的对数正态分布，其余主要仿 真参数如表 1 所示。 实验仿真参数 表 1 参数 小区半径/m 高斯白噪声 N0/dBm 系统带宽 W/kHz 电路功率 Pcir/mW 蜂窝链路路径损耗模型/dB D2D 链路路径损耗模型/dB CR /(Mbit·s−1) DR /(Mbit·s−1) 蜂窝链路最小传输速率 min D2D 链路最小传输速率 min D2D 用户间最大传输距离 Dmax/m 蜂窝用户数 K/个 D2D 用户数 N/对 中继数 L/个 取值 500 −114 180 50 128.1+37.6lnd 140+40lnd 0.9 0.9 50~150 10~20 5~15 50~150 仿 真 中 ， 将 本 文 所 提 算 法 与 文 献 [13] 的 BEEPER 算法、随机中继选择算法和随机信道分配 算法进行对比。其中，文献[13]的 BEEPER 算法分 别优化 D2D 中继通信的第一跳和第二跳链路的能 效，然后再完成中继选择，但是并没有考虑信道的 分 配 ， 所 以， 为 了 全 面评 价 本 文 所提 算 法 ， 与 BEEPER 算法进行对比时，在 BEEPER 算法中加入 了本文提出的信道分配算法。随机中继选择算法是 本文所提功率控制和信道分配算法的结合，而每个 D2D 用户的辅助中继是从备选中继区域中随机选 择的。随机信道分配算法是本文所提功率控制和中 继选择算法的结合，而信道的分配是随机的。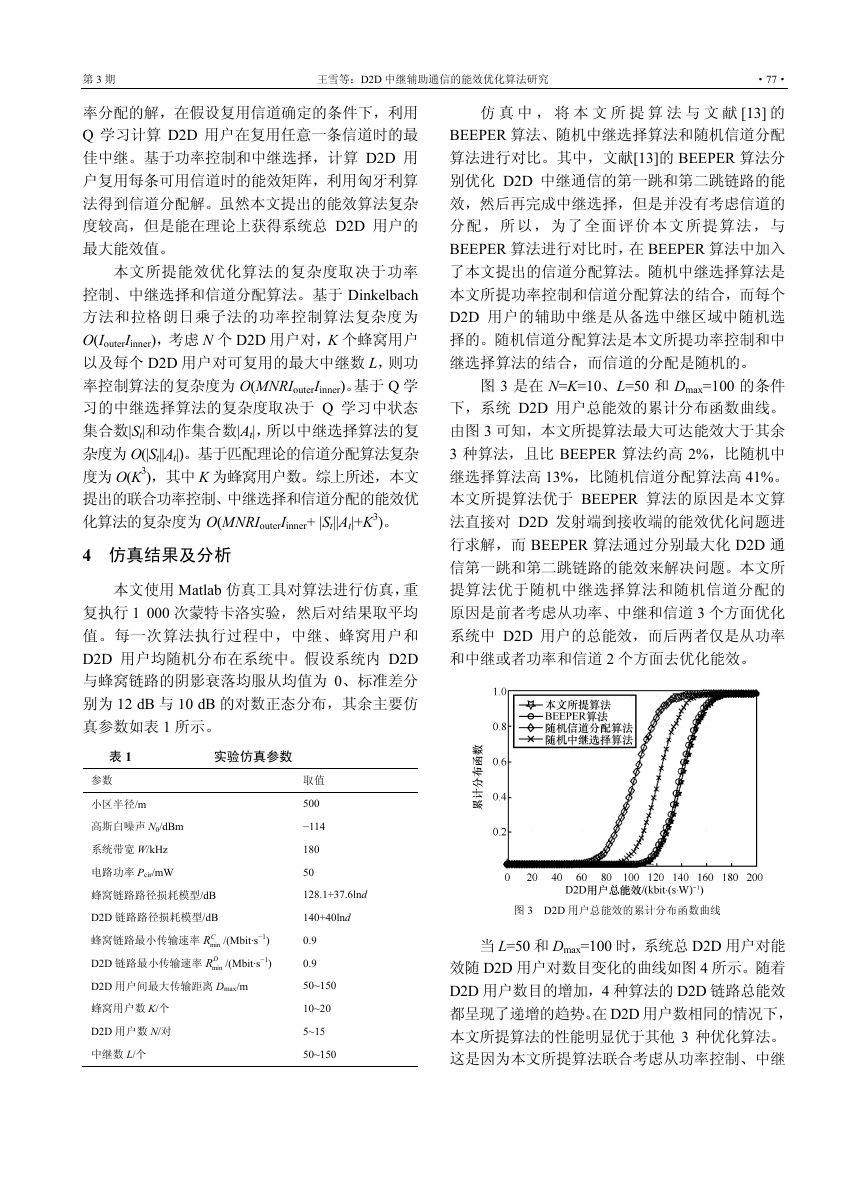 图 3 是在 N=K=10、L=50 和 Dmax=100 的条件 下，系统 D2D 用户总能效的累计分布函数曲线。 由图 3 可知，本文所提算法最大可达能效大于其余 3 种算法，且比 BEEPER 算法约高 2%，比随机中 继选择算法高 13%，比随机信道分配算法高 41%。 本文所提算法优于 BEEPER 算法的原因是本文算 法直接对 D2D 发射端到接收端的能效优化问题进 行求解，而 BEEPER 算法通过分别最大化 D2D 通 信第一跳和第二跳链路的能效来解决问题。本文所 提算法优于随机中继选择算法和随机信道分配的 原因是前者考虑从功率、中继和信道 3 个方面优化 系统中 D2D 用户的总能效，而后两者仅是从功率 和中继或者功率和信道 2 个方面去优化能效。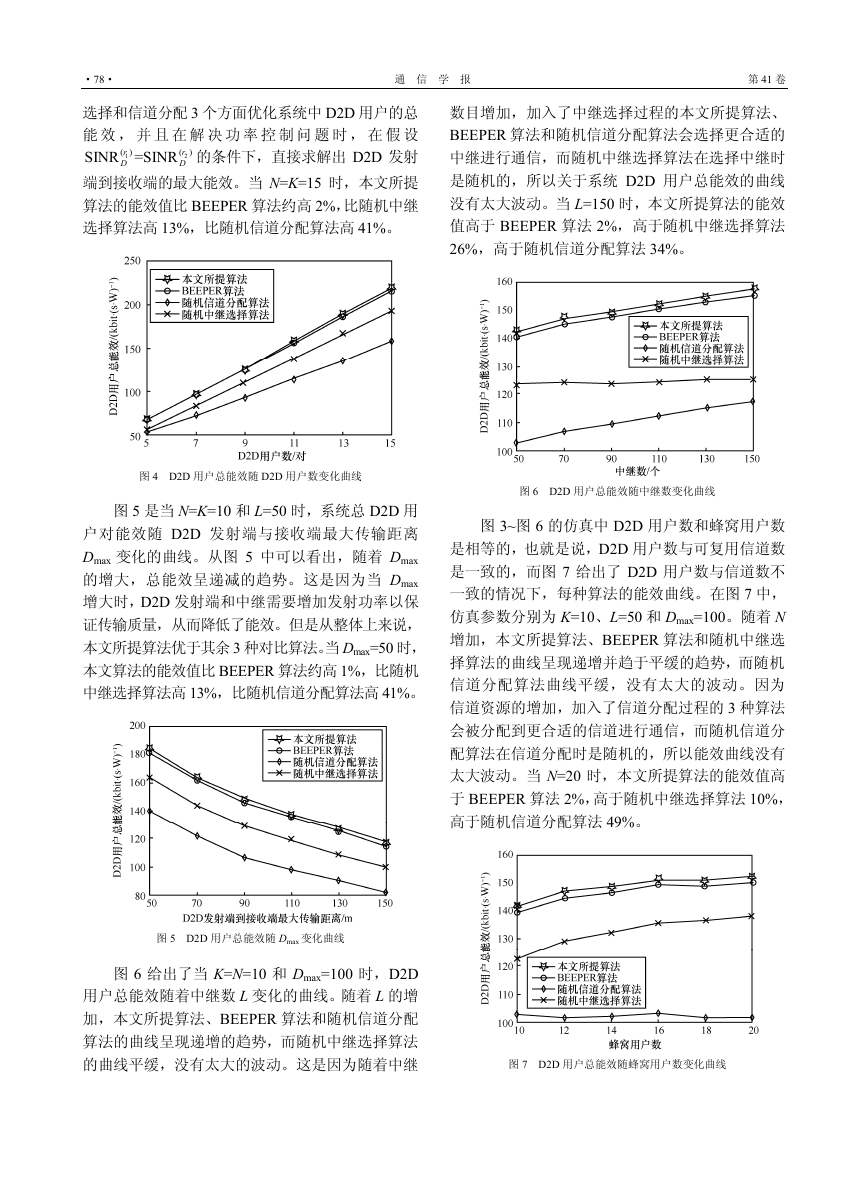 图 3 D2D 用户总能效的累计分布函数曲线 当 L=50 和 Dmax=100 时，系统总 D2D 用户对能 效随 D2D 用户对数目变化的曲线如图 4 所示。随着 D2D 用户数目的增加，4 种算法的 D2D 链路总能效 都呈现了递增的趋势。在 D2D 用户数相同的情况下， 本文所提算法的性能明显优于其他 3 种优化算法。 这是因为本文所提算法联合考虑从功率控制、中继
    ·78· 通 信 学 报 第 41 卷 ) r ( 1 D 选择和信道分配 3 个方面优化系统中 D2D 用户的总 能 效 ， 并 且 在 解 决 功 率 控 制 问 题 时 ， 在 假 设 D 的条件下，直接求解出 D2D 发射 SINR =SINR r ( ) 2 端到接收端的最大能效。当 N=K=15 时，本文所提 算法的能效值比 BEEPER 算法约高 2%，比随机中继 选择算法高 13%，比随机信道分配算法高 41%。 数目增加，加入了中继选择过程的本文所提算法、 BEEPER 算法和随机信道分配算法会选择更合适的 中继进行通信，而随机中继选择算法在选择中继时 是随机的，所以关于系统 D2D 用户总能效的曲线 没有太大波动。当 L=150 时，本文所提算法的能效 值高于 BEEPER 算法 2%，高于随机中继选择算法 26%，高于随机信道分配算法 34%。 图 4 D2D 用户总能效随 D2D 用户数变化曲线 图 5 是当 N=K=10 和 L=50 时，系统总 D2D 用 户对能效随 D2D 发射端与接收端最大传输距离 Dmax 变化的曲线。从图 5 中可以看出，随着 Dmax 的增大，总能效呈递减的趋势。这是因为当 Dmax 增大时，D2D 发射端和中继需要增加发射功率以保 证传输质量，从而降低了能效。但是从整体上来说， 本文所提算法优于其余 3 种对比算法。当 Dmax=50 时， 本文算法的能效值比 BEEPER 算法约高 1%，比随机 中继选择算法高 13%，比随机信道分配算法高 41%。 图 6 D2D 用户总能效随中继数变化曲线 图 3~图 6 的仿真中 D2D 用户数和蜂窝用户数 是相等的，也就是说，D2D 用户数与可复用信道数 是一致的，而图 7 给出了 D2D 用户数与信道数不 一致的情况下，每种算法的能效曲线。在图 7 中， 仿真参数分别为 K=10、L=50 和 Dmax=100。随着 N 增加，本文所提算法、BEEPER 算法和随机中继选 择算法的曲线呈现递增并趋于平缓的趋势，而随机 信道分配算法曲线平缓，没有太大的波动。因为 信道资源的增加，加入了信道分配过程的 3 种算法 会被分配到更合适的信道进行通信，而随机信道分 配算法在信道分配时是随机的，所以能效曲线没有 太大波动。当 N=20 时，本文所提算法的能效值高 于 BEEPER 算法 2%，高于随机中继选择算法 10%， 高于随机信道分配算法 49%。 图 5 D2D 用户总能效随 Dmax 变化曲线 图 6 给出了当 K=N=10 和 Dmax=100 时，D2D 用户总能效随着中继数 L 变化的曲线。随着 L 的增 加，本文所提算法、BEEPER 算法和随机信道分配 算法的曲线呈现递增的趋势，而随机中继选择算法 的曲线平缓，没有太大的波动。这是因为随着中继 图 7 D2D 用户总能效随蜂窝用户数变化曲线
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料