第1页 / 共32页
第2页 / 共32页
第3页 / 共32页
第4页 / 共32页
第5页 / 共32页
第6页 / 共32页
第7页 / 共32页
第8页 / 共32页
现代信号处理复习题.doc
49、简述AR模型功率谱估计的方法
式中 0f =100HZ,以采样频率 sf =400Hz对 ( )
ax t 进行采样，得
)
f t
0
2cos(2
( )
ax t
ax t 和时域离散信号 ( )
ax t 的傅里叶变换表示式 (
ax t 和 ( )
x n 的表达式；
1、已知
到采样信号 ˆ ( )
（1）写出 ( )
（2）写出 ( )
（3）分别求出 ( )
解：（1）
ax t 的傅里叶变换和 ( )
)
( )
x t e
a
dt
t
j
a
(
X j
e
j
t
0
(
e
j
t
0
)
e
t
j
dt
x n ，试完成下面各题：
aX j ；
)
x n 的傅里叶变换。
2cos(
)
t e
0
dt
t
j
上式中指数函数和傅里叶变换不存在，引入奇异函数函数，它的傅里叶变换可以表示成：
(
aX j
（2）
2 [ (
(
)]
)
)
0
0
ˆ ( )
x t
a
( )
x n
n
2cos(
x t
a
( ) (
0
nT
),
t nT
)
n
n
2cos(
nT
0
) (
t nT
)
，信号最高频率1KHz,是确
F
Hz
50
2、用微处理器对实数序列作谱分析，要求谱分辨率
定以下各参数：
pT
（1）最小记录时间 min
（2）最大取样时间 maxT
（3）最少采样点数 minN
（4）在频带宽度不变的情况下将频率分辨率提高一倍的N值。
解：（1）已知
（2）
T
max
1
2 10
0.5
ms
3
F
pT
min
50
Hz
1
F
1
1
50
0.02
s
1
2
f
max
0.02
s
3
0.5 10
s
f
min
s
pT
T
N
（3）
（4）频带宽度不变就意味着采样间隔T 不变，应该使记录时间扩大一倍为0.04s实频率
min
40
分辩率提高1倍（ F 变成原来的1 2 ）
N
min
pT
T
0.04
s
3
0.5 10
s
80
3、在时域对一有限长的模拟信号以4KHZ采样，然后对采到的N个抽样做N点DFT，所得离
散谱线的间距相当于模拟频率100HZ。某人想使频率能被看得清楚些，每50HZ能有一根谱
线，于是他用8KHZ采样，对采到的2N个样点做2N点DFT。问：他的目的能达到吗？
答：不能，因为他忽略了数字频率和模拟频率的区别。
提高采样频率 sf ， N 固然大了，数字频率（单位圆）上的样点数确实增加了，但从
模拟频率谱看，样点一点也没有变得密集，这是因为数字频率 2 总是对应模拟频率 sf 。
采样频率由 sf 到2 sf 增加一倍，N 也增加一倍，但模拟频率的采样间隔
Hz
100
2
2
f
s
N
f
s
N
1
一点也没有变。所以，增大采样频率，只能提高数字频率的分辨率
高模拟频率的分辨率。
2(
N
2
2
N
)
，不能提
4、在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器，他们分别起什么作用
？
解：在 DA/ 变换之前让信号通过一个低通滤波器，是为了限制信号的最高频率，使其满
足当采样频率一定时，采样频率应大于等于信号最高频率2倍的条件。此滤波器亦称为“抗
折叠”滤波器。
在 AD / 变换之后都要让信号通过一个低通滤波器，是为了滤除高频延拓谱，以便把
抽样保持的阶梯形输出波平滑化，故又称为“平滑”滤波器。
1
0,
1
)(
zH
a
1(
)(zH 的极点为
z
a
5、已知
，分析其因果性和稳定性。
2
a
)
1)(
az
,
a
a z
，
1
az
z
，对应的系统是因果系统，但由于收敛域不包含单位圆，因此是
解：
（1） 收敛域 1
不稳定系统。单位脉冲响应 ( )
h n
0
z
（2）收 敛 域
n
( )
a u n
h n
，这是一个非因果且不收敛的序列。
a
a
，对应的系统是一个非因果系统，但由于收敛域包含单位圆，因此
（3）收敛域
是稳定系统。其单位脉冲响应 ( )
h n
， 对 应 的 系 统 是 非 因 果 且 不 稳 定 系 统 。 其 单 位 脉 冲 响 应
1)
a ，这是一个收敛的双边序列。
，这是一个因果序列，但不收敛。
) (
z
) ( )
u n
(
a
a
n
(
a
n
n
a
1
1
n
6、什么叫做数字滤波器？FIR和IIR的比较和各自的设计方案？
答：所谓数字滤波器，是指输入、输出均为数字信号，通过一定运算关系改变信号所含频率
成分的相对比例或者滤除某些频率成分的器件。
FIR：有限脉冲响应滤波器
IIR：无限脉冲响应滤波器
★ IIR极点可存在与单位圆的任何地方,有较强的幅度选择性,但相位特性差。
FIR相位呈线性，但幅度特性需高阶才可调节的较好。
★ FIR计算不产生振荡,误差影响小,可以采用FFT算法。
IIR有稳定问题，有限字长可能产生振荡，同阶递归算法速度受到限制。
★ IIR可用模拟滤波器成果，得到有效的封闭式公式，设计工作量小，要求低。
FIR仅窗函数有公式，但无显式表达通、阻带，需要计算机辅助设计。
★ IIR设计已规格化，频率特性为分段常数的滤波器。
FIR主要适应特殊应用，且高阶IIR不易达到指标的滤波器。
ＩＩＲ数字滤波器设计
★直接设计：
原型变换（由一低通经过频率变形设计低通、高通、带通、带阻等）
频域设计（零、极点配置；幅度平方函数），
时域设计（帕德（Pade）逼近；波形形成）
★ 优化技术设计（依据一定的优化准则进行设计）
★
ＦＩＲ数字滤波器设计
★线性相位：
偶对称：
★窗函数（时域加权平均）：矩形，三角，余弦，布莱克曼(Blackman)系列，凯塞(Kaiser)系
列，高斯
零点的镜像存在。
奇对称：
2
★频率取样：在H(z)的单位圆上等分取样(是否带初相)
★优化技术设计：（依据一定的优化准则进行设计）
8：长度为N=10的两个有限长序列
)(2
)(1
nx
nx
,1
0
,0
5
)(1 nx 、
作图表示
)(2 nx
4
n
9
n
)(2 nx
和
)(1 nx 、
)(
ny
)(
nx
1
和
)(
ny
解：
,1
,1
)(
nx
1
)(
nx
2
9
0
4
n
5
n
)(
nx
(圆周卷积)，循环卷积区间长度L=10。
2
分别如题3解图（ a ）、（b ）、（ c ）所示
9：若序列 ( )h n 是因果序列，其傅里叶变换的实部为 (
及其傅里叶变换 (
)jH e 。
j
RH e
) 1 cos(
)
，求序列的 ( )h n
) 1
1
2
e
j
1
2
j
e
( )]
FT h n
[
e
n
( )
h n e
e
j n
解：
(
H e
R
( )
h n
e
n
0
1
) 1 cos(
j
1 ,
2
1,
n
1 ,
2
0,
0
n
( ),
0
h n n
e
2 ( ),
0
h n n
e
( )
h n e
1
n
n
( )
h n
(
H e
j
)
0
1,
n
1,
1
n
0,
other n
j n
1
e
j
2
e
j
/ 2
cos
2
3
10、什么是宽平稳随机过程？什么是严平稳随机过程？它们之间有什么联系？
答：若一个随机过程的数学期望与时间无关，而其相关函数仅与有关，则称这个随机过程
是宽平稳的或广义平稳的。所谓严平稳随机过程是指它的任何n维分布函数或概率密度函数
与时间起点无关。严平稳的随机过程一定是宽平稳的，反之则不然。
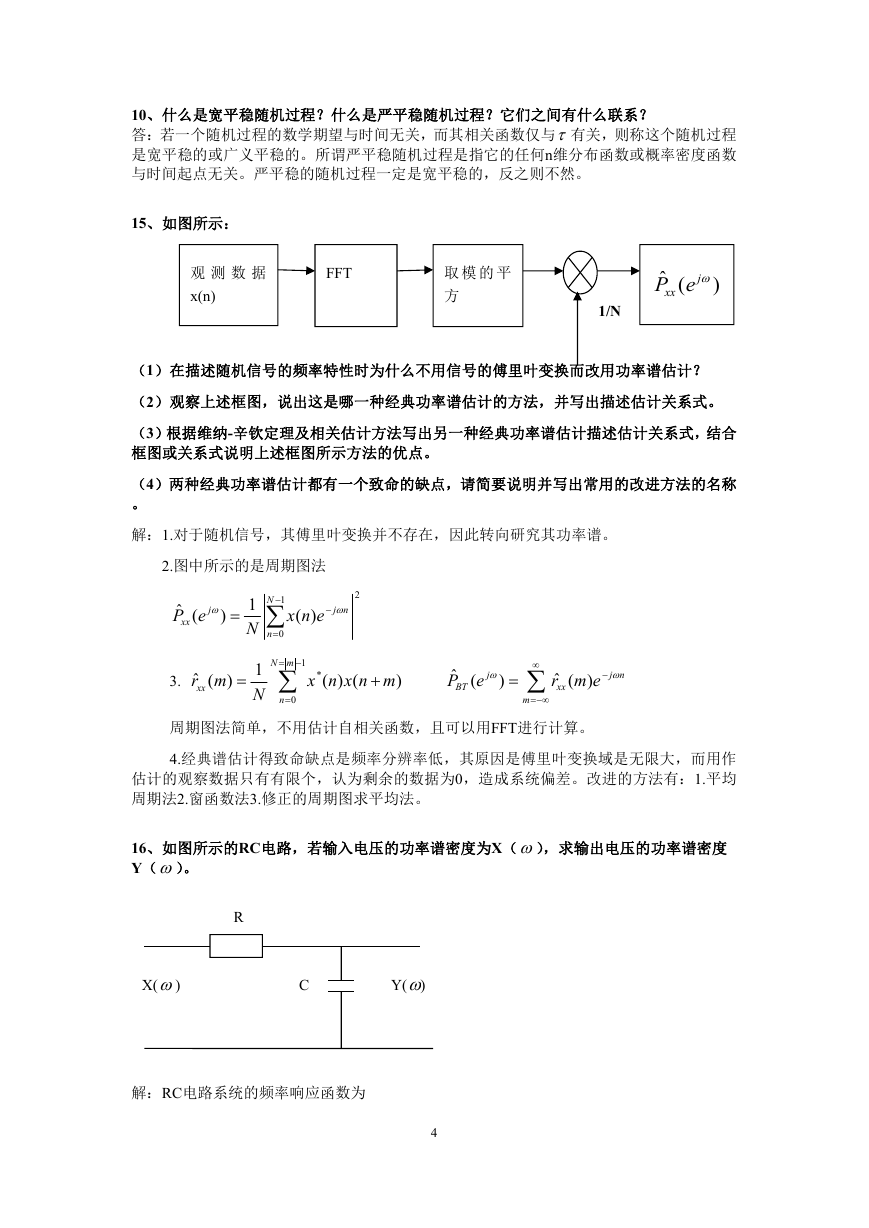
15、如图所示：
观 测 数 据
x(n)
FFT
取 模 的 平
方
ˆ (
)j
xxP e
1/N
（1）在描述随机信号的频率特性时为什么不用信号的傅里叶变换而改用功率谱估计？
（2）观察上述框图，说出这是哪一种经典功率谱估计的方法，并写出描述估计关系式。
（3）根据维纳-辛钦定理及相关估计方法写出另一种经典功率谱估计描述估计关系式，结合
框图或关系式说明上述框图所示方法的优点。
（4）两种经典功率谱估计都有一个致命的缺点，请简要说明并写出常用的改进方法的名称
。
解：1.对于随机信号，其傅里叶变换并不存在，因此转向研究其功率谱。
2.图中所示的是周期图法
ˆ (
P e
xx
j
)
N
1
1
N
n
0
2
( )
x n e
j n
3.
ˆ (
r m
xx
)
1
N
N m
1
n
0
*
x n x n m
( ) (
)
ˆ
(
P e
BT
j
)
m
ˆ
)
r m e
xx
(
j n
周期图法简单，不用估计自相关函数，且可以用FFT进行计算。
4.经典谱估计得致命缺点是频率分辨率低，其原因是傅里叶变换域是无限大，而用作
估计的观察数据只有有限个，认为剩余的数据为0，造成系统偏差。改进的方法有：1.平均
周期法2.窗函数法3.修正的周期图求平均法。
16、如图所示的RC电路，若输入电压的功率谱密度为X（），求输出电压的功率谱密度
Y（）。
R
X()
C
Y()
解：RC电路系统的频率响应函数为
4
H（） =
H（）
2
=
R
1
Cj
1
Cj
1
(
)
RC
2
=
1
RCj
1
1
由线性系统的输出谱密度与输入谱密度之间的关系可得：
Y（） =
H（）
2
* X（）=
)X(
2
)
(
RC
1
X
R
Y
)(
)(
、
17、已知LTI系统的传输函数为h（t），输入是实平稳随机过程X（t），输出是Y（t），求
R
解：平稳随机过程经过LTI系统输出还是平稳随机过程，所以
R
Y
三者间的关系？
()([
tYtYE
)(
th
和
)]
)(
[
duuhutXE
)()
(
(
tX
)()
vhv
dv
]
[
(
tXutXE
)
(
)()(
)]
vhuhv
dudv
R
X
(
)()()
vhuhvu
dudv
R
)(
(
h
其中 是卷积运算。
)(
h
X
)
18、常用的自适应滤波理论与算法有哪些？
从理论上讲，自适应滤波问题没有惟一的解。为了得到自适应滤波器及其应用系统，
可以采用各种不同的递推算法，这些自适应算法都有各自的特点，适用于不同场合。
常用的自适应滤波理论与算法有：
（1）、基于维纳滤波理论的方法。
（2）、基于卡尔曼滤波理论的方法。
（3）、基于最小均方误差准则的方法。
（4）、基于最小二乘准则的方法。
19、简述自适应信号处理技术的应用
自适应滤波处理技术可以用来检测平稳的和非平稳的随机信号。常应用于：
（1）、自适应滤波与逆滤波。
（2）、系统辨识。
（3）、自适应均衡。
（4）、自适应回波抵消。
（5）、自适应噪声抵消与谱线增强。
（6）、自适应谱估计。
（7）、自适应波束形成。
（8）、自适应神经智能信息处理。
（9）、盲自适应信号处理。
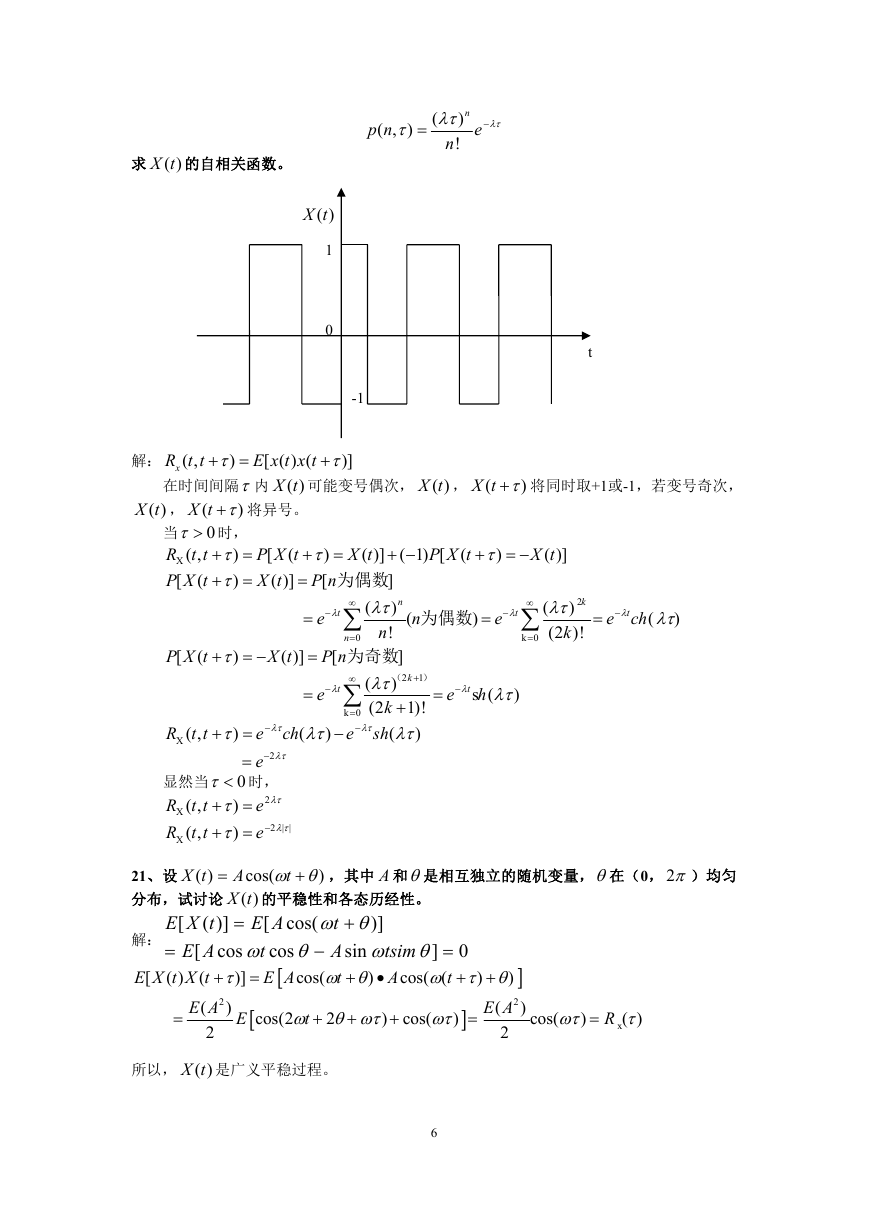
20、设 ( )X t 为一随机电报信号，其样本函数如图1所示，取+1，-1概率相等，在时间间隔
内波形变号次数服从参数为的泊松分布，即：
5
求 ( )X t 的自相关函数。
( , )
p n
n
)
(
!
n
e
( )X t
1
0
-1
t
解： ( ,
xR t t
在时间间隔内 ( )X t 可能变号偶次， ( )X t ， (
[ ( ) (
E x t x t
)]
)
X t 将同时取+1或-1，若变号奇次，
)
( 1) [
(
P X t
)
X t
( )]
(
)
n
为偶数
t
e
k 0
2
k
(
)
(2 )!
k
t
e
ch
(
)
t
e
s (
h
)
n
t
e
X t
n
[
P n
)
( )]
]
[
P n
为偶数
)
(
!
n
]
为奇数
1
2
k
(
)
（
）
1)!
(2
k
k 0
(
)
e
sh
(
)
e
t
0
( )X t ， (
X t 将异号。
)
当 0 时，
X( ,
)
R t t
[
)
(
P X t
[
(
P X t
( )]
X t
[
(
P X t
)
X t
( )]
e
)
X( ,
R t t
ch
2e
显然当 0 时，
2
X( ,
e
R t t
2 |
|
X( ,
e
R t t
)
)
，其中 A 和是相互独立的随机变量，在（0， 2 ）均匀
)(
tX
21、设
分布，试讨论 )(tX 的平稳性和各态历经性。
)
cos(
A
t
解：
(
[
cos(
)]
)]
[
tXE
AE
t
sin
cos
]
cos
[
A
AE
t
[
)
( )
(
cos(
)
cos(
)]
E X t X t
t
E A
2
2
(
(
)
E A
E A
2
2
tsim
A
) cos(
cos(2
)
0
(
t
E
2
)
t
)
所以， )(tX 是广义平稳过程。
6
cos(
)
R
( )
x
A
cos(
)
dt
t
0
[
(
tXE
)]
T
__
X
1
2
T
T
dt
)(
t
lim
T
因此， )(tX 具有均值各态历经性。
__________
)(
(
tXtX
______
)
lim
T
(
tXtX
)(
T
1
2
T
T
T
1
2
T
lim
T
T
)
dt
T
T
T
T
A
cos(
)
t
A
cos(
)
dt
(
t
)
2
A
2
[cos
t
cos(
2
])2
t
dt
lim
T
1
2
T
1
lim
2
T
T
2
A
2
(
tw
cos
因此， )(tX 不具有自相关函数各态历经性。
)(
R
)
t
X
2
1
22、从最速下降法出发：
W
1j
W
j
j
其中， 1jW 是第j+1个抽样时刻的滤波器权矢量， 控制收敛稳定性和速率， 是误
差-性能曲面的真实梯度，推导自适应噪声消除的 Widrow-Hopf 的LMS算法。
解答：
梯度矢量▽，初级输入与刺激输入的互相关P以及初级输入的自相关R之间的关系为：
= 2 +2RWP
在LMS算法中，使用 的瞬时估计，则有
T
j =-2 jP +2 jR
=-
(
X y
j
j
e
j
y
X W
j
j
2
其中
jX jy +2 jX
jW =-2
2
e X
j
j
X W
)
T
j
j
j
jX
jW
(1)
用（1）式替换最速下降法的梯度，我们得到基本的Widrow-Hopf 的LMS算法：
1
其中 je = y
jW X
W
j
e X
2
T
W
j
j
j
j
j
23、自适应滤波器的特点及应用范围
答案：由于滤波器的参数可以按照某种准则自动地调整到满足最佳滤波的要求；实现时不需
要任何关于信号和噪声的自相关特性，尤其当输入统计特性变化时，自适应滤波器都能调整
自身的参数来满足最佳滤波的需要，即具有学习和跟踪的性能。当符合下面几个情况时都可
以应用自适应滤波(1)需要滤波器特性变化以自适应改变的情况时（2）当信号和噪声存在频
谱重叠时（3）噪声占据的频谱是时变或未知。例如电话回声对消，雷达信号处理，导航系
统，通信信道均衡和生物医学信号增强。
24、已知输入信号向量U(n)的相关矩阵R及期望响应信号 ( )d n 的互相关向量P分别为
R=
2 1
1 2
，
P= 5 4 T
且已知期望响应 ( )d n 的平均功率为 E{
(1) 计算维纳滤波的最优权向量；
(2) 推导误差性能面的表达式；
2( )
d n }=30
7
(3) 计算最小均方误差。
答案：（1）由 0
0
RW P 可得
2 1
1 2
1
0W R P
=
1
5
4
=
2
1
（2）假设在 n 时刻，输入信号为 ( )u n ，横向滤波器输出信号
( )
)
,
*
H
ˆ( )
T
( )
w u n
u n w
d n
ˆ
(
)
(
)
(
d n
e n
d n
*
{ ( )
( )}
(
)
E e n e n
J w
H
{[ ( )
( )][ ( )
E d n w u n
d n
2
H
{ ( ) }
{ ( )
E d n
E d n u
2
H
H
p w w p w R
d
w
（3）把 0W 代入 (
J w 得：
)
H
J w
(
)
0
2
d
H
p w
0
30
5
4
2
1
16
T
u n w
H
( )}
n w w E u n d n
* *
] }
{ ( )
( )
*
( )}
H
{ ( )
w E u n u
H
( )}
n w
}
),
Tt
是 宽 平 稳 随 机 过 程 ？ 并 证 明 随 机 过 程
是宽平稳过程，其中，Y , Z是相互独立的随机变量，且
}
),
Z
({
tX
Y
EZ
sin(
DZ
)
cos(
t
,0
DY
)(
tmX
),(
tsR
，
X
Tt
是二阶矩过程；
)(
tEX
常数；
(
[
)(
tXsXE
({
tX
25 、 怎 样 判 断 随 机 过 程
)(
),
0
tX
t
t
2
EY
。
答：（1）如果 )(tX 满足，如下条件：
（a）
（b）对任意 Tt ，
Tts ,
（c）对任意
稳随机过程。
（2）
证明：
2
[
(
))
(
sin(
)
cos(
[(
tXE
Y
t
Z
t
YE
2
2
cos(
)
[
2)
sin(
(
)
YE
t
YZ
Z
t
t
2
2
2
[
)
[
(
sin]
)
(
[
YE
YZE
t
t
ZE
EY
因为Y,Z是相互独立的随机过程，且
2
2 tXE
[
)]
(
=
[
)(
)
cos(
Z
YE
tEX
t
(
)]
[
),(
)(
tsRX
tXsXE
2
cos(
)
[
cos(
)
s
YE
t
2
(
)]
s
t
只与时间间隔有关，与时间起点无关。
所以，
Tt
是宽平稳随机过程。
)]
cos
cos
]
({
tX
cos[
),
}
2
)]
(
sR
X
t
)
。则判定
({
tX
),
Tt
是宽平
}
)
cos(
t
Z
2
2
)]
(
sin
t
cos(
2](
)
t
,0
EZ
DY
sin(
t
))]
sin(
t
DZ
))
2
，所以
)]
sin(
[
]
sin(
)
)
][
cos(
t
t
ZE
t
YE
))
cos(
cos(
[(
)
sin(
(
YE
Z
t
Y
s
s
2
sin(
)]
(
))
)
sin(
sin(
s
YZ
t
Z
t
s
0
)
=常数
sin(
Z
t
))]
，
),(
tsRX
26、若
性质？
),
({
tX
)(XR
}
Tt
为均方连续的实平稳随机过程，则其自相关函数
在计算其功率谱
时有什么作用？
(XS
)
)(XR
具有那些常用
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
