极区飞行格网惯性导航算法原理.pdf-资料库

2013年 4月第 31卷第 2期西北工业大学学报 Journ al of Northwestern Polyteehnical University Apr． 2013 Vo1．31 No．2 极区飞行格网惯性导航算法原理周琪，秦永元，付强文，岳亚洲 (1．西北工业大学自动化学院，陕西西安 710072；2．飞行自动控制研究所，陕西西安 710065) 摘要：为克服极区飞行时地理经线收敛引起传统机载惯性导航系统力学编排方案无法定位定向的问题，提出了格网坐标系下的惯导力学编排方案。该方案．-q-~直接获得格网航向而无需任何外界参考信息，地心地固坐标系下的位置坐标替代传统经纬度坐标可直接用于飞机定位。推导的格网导航坐标系下的导航误差方程可方便用于组合导航算法设计。仿真分析表明格网导航算法误差特性同常规导航方案的误差特性一致，可以满足极区飞行时飞机的导航需要。关键词：极区导航；格网导航；惯性导航；误差方程中图分类号：U666．1 文献标识码：A 文章编号：1000．2758(2013)02-0210-08 1903年莱特兄弟发明飞机以后，飞机逐渐成为排在高纬度地区存在方位陀螺施矩困难、计算溢出极地探险、科考的主要工具之一。1914年前苏联皇和误差放大等问题。。为克服指北方位力学编排家海军上尉 Y．I．Nagurskiy驾驶飞机第一次飞抵高的上述难题，可采用对方位陀螺不施矩的自由方位纬度地区开启了飞机极地探险的新纪元。在极区由于地理经线收敛、地磁力线收敛、磁场异常导致惯导力学编排或仅跟踪地球自转的游移方位惯导力学编排。。由于引入了位置方向余弦矩阵，可有基于传统磁罗盘的飞机定位定向方式不再适用于极效解决方位陀螺施矩困难、计算溢出的难题，但是在区飞机导航。极区导航面临经线收敛无可用的航向参考线和缺乏可靠的方向跟踪设备，两大难题逐渐凸显并成为极区导航的研究热点 1-3]。 1941年英国高纬度地区从位置方向余弦矩阵提取位置信息时存在奇异值。另外在高纬度地区飞机所在地游移角同经度相关不能分离且游移角的计算误差随纬度升高皇家空军中校 K．C．Maclure在其论文 “Polar Naviga．而放大甚至溢出，因此游移方位惯导力学编排方案 tion”中提出了格网导航的概念并建议用陀螺作为在高纬度地区不输出位置和方位信息的条件下可正方位跟踪设备 ¨ J，并于 1945年用该方法完成了常工作但无法完成定向和定位任务【' j。在计算 Aries I飞向北极点的导航任务，这使得极区导航面临的两大难题迎刃而解 ,6j。1958年 8月 3 日装备机有效字长较短的平台惯导时代，游移方位惯导力学编排不失为一种可在全球大部分地区执行正常导了惯性导航设备的美国海军 “鹦鹉螺 ”号核潜艇潜航任务的有效方案，如早期的 LN．51航空惯导系统航 21天后成功穿越北极点，这一震惊世界的壮举充便采用该方案 ¨ 。除自由和游移方位力学编排外，分显示了惯性导航系统有别于其它导航系统的独特优点：自主性、隐蔽性、信息的完备性 J。随着技术 ECEF力学编排和惯性坐标系力学编排同样具备全球导航能力，但输出的导航参数物理意义不明确，不的成熟和成本的降低，民用航空和军用飞机逐渐装利于飞行员和领航员操作 ¨ 。由于惯导高度通道备了惯性导航系统，并成为机载主要导航设备。装是发散的，任何非水平坐标的惯导力学编排方案都载惯导设备的飞机逐渐具有极区飞行能力且与自动驾驶仪交联可实现自主极区飞行。存在不稳定的因素，不能远距离长时间稳定工作，佗]。除上述常见力学编排外，横向地球坐标力惯性导航具有多种力学编排方案，其中指北方位惯导力学编排概念简单、物理意义明确，但指北编学编排通过人为将地球极点移到赤道上的方式可克服极区定位定向难题。横向地球坐标力学编排是在收稿日期：2012-04．26 基金项目：国家自然科学基金(61273333)资助作者简介：周琪 (1984一 )，西北工业大学博士研究生，主要从事导航、制导与控制研究。

第 2期周琪等：极区飞行格网惯性导航算法原理假设地球是圆球的条件下推导的，存在原理性的误差 ’”’ J。在计算机水平相对较低的早期通常采用 G为格网坐标系，如图 1所示，以飞机所在地 P 点处平行于格林威治子午面的平面作为格网平面，该种力学编排方案，如 “鹦鹉螺 ”号核潜艇装备的惯以飞机所在地的水平面作为切平面，格网平面与切导系统便采用该种力学编排方式 J。文献 [13]介平面的交线定义为格网北向，格网北向同真北方向绍的极圈力学编排是以飞机进入极区点位置的地理的夹角为 or，格网天向同地理天向重合，格网东向在坐标系相对地球凝固作为导航参考坐标，其实质是切平面内且与格网北向垂直构成右手直角坐标系，平面导航编排。虽计算简单，但作用范围较小，存在此即为格网坐标系，各轴单位向量集记为 ( ，P ，原理性计算误差。文献 [14]介绍了一种相对能构， )。可见格网坐标系是 P点处的水平坐标系，当 P 成圆锥或圆柱可展曲面定位的惯导力学编排方式，点在地球表面移动时，大圆飞行时格网航向始终该编排方案可输出 ECEF坐标，但整个力学编排数不变。学关系复杂，物理意义不明确。文献 [17]在格网坐标框架下推导了地球是圆球模型下的格网惯性力学编排，由于以格林威治子午线作为飞机航向参考可避免纬度升高经线收敛造成的定向参考难题，其输出 ECEF坐标下的位置信息可方便同极区航图配合使用，因此格林威治格网导航编排是目前较适宜的极区惯性导航编排方案。在计算机水平较低的早期，圆球模型下的格网力学编排是一种折中方案。随着计算机水平的提高以及对导航精度要求的提高，符合真实地球形状的地球模型下的格网力学编排方案呼之欲出。本文在文献 [17]的基础上推导了地球是 WGS．84参考旋转椭球模型的格网惯性导航力学编排，并对相关误差进行了仿真分析。 1 坐标系定义 i为地心惯性坐标系，以地心为坐标原点，z轴沿地球自转轴方向，和 Y轴在赤道平面内并指向某二恒星。 e为地心地固坐标系 (ECEF)，与地球固连，相对惯性坐标系以地球自转角速度旋转。地球坐标系的原点在地心，z轴沿地球自转轴的方向，轴在赤道平面内与本初子午线相交，Y轴也在赤道平面内，与、轴构成右手直角坐标系。 b为载体坐标系，原点位于飞机的质心，沿飞机横轴向右，Y沿飞机纵轴向前，沿飞机立轴向上， xyz构成右手直角坐标系。载体坐标系与 IMU的体坐标系重合。 g为地理坐标系，原点位于飞机所在点，z轴沿地理垂线指向上，、Y轴在当地水平面内且轴沿当地纬线切线方向指向东，Y沿当地经线方向指向北，即“东北天 (ENU)”地理坐标系。图 1 格网坐标系在上图中各坐标系间的转换关系为： 1)地球和地理坐标系间的转换 [_c罴 -c ] 式中，(P ，er，P )为地球坐标系各轴单位向量集合，(P ，P ，e )为地理坐标系内各轴向单位向量集合 · 『一sinA cosA 0] = I—sinLcosA —sinLsinA cosL l (2) L c。s c。sA c。sLsinA sinL j 式中为位置方向余弦矩阵。 2)地理和格网坐标系问的转换 rPGE] r—COSO" I l 1 ． n ]l(3 - J

· 2l2· 西北工业大学学报第 31卷 = 3)地球和格网坐标系间的转换 (4) 稚Il _c 厂一 coso'sinA + sino'cosA sinL cosorcosA + sintrsinLsinA c =I —sintrsinA—cos(rsin￡c0sA sintrcosA—cos(rsinLsinA cosLcosA cosLsinA (5) (6) 4)真北向与格网北向间夹角 or 从格网北向与真北向夹角的定义以及图 1可以看出单位向量 e。和 e 相互垂直，因此满足内积为零的关系 eG ·ey=0 (7) = c6GJ b (14) b G^ l6一 G G b6 一 ^ ； cc， b — cb G (15 一L GO．~iG L ) 式中 c 的初值由初始对准获得或者由当地地理导航坐标系内的方向余弦矩阵 C；经变换而来：其中单位向量 e。和 e 可通过 (1)式和 (3)式的关 c = c 系用地理坐标系内的单位向量表示此外 eG ～：sino'eE+coso-e『v+0·eU (8) ~．OiGG G + ∞ eG ． G ey=cosAeF—sinLsinAeⅣ+cosLsinAeU (9) 由内积的坐标表示及 (7)式的关系可得 sintrcosA —cosorsinLsinA = 0 (10) 所以． sl。nor： _ = ——二二二二二======二 ,／1一COS Lsin A 也己 cos ： _ = 兰 ,／1一COS Lsin A (11) 【l 1) (12) 5)飞机航向 G = C Gll，g ‘e 位置速率 ∞Gc的求解如下 r ] G I c l G l∞ l l G l (cJ eGz l l ^G R c 1 R G 1 r 一 R G fG 飞机航向定义为飞机纵轴与真北方向的夹角，北偏东为正，记为；而格网航向角定义为飞机纵 = R G + COS — or R Mh 。 R 轴与格网北向的夹角，北偏东为正，记为。由图 1 一 1 R = O" COS — — R 所示格网北向和真北方向的关系可以得到飞机真实 G M h + R N 航向角同飞机格网航向角间的关系： f 一 1 i 。【一 J m 吣，v： +or (13) (16) (17) (18) (2O) ～ (21) (22) ( (23) L Zj J 2 格网惯性导航力学编排格网导航坐标系同游移方位坐标系是同一类坐标系，只不过格网坐标系相较于游移方位坐标系更特殊，因此格网导航坐标系内的惯导力学编排同游移方位惯导系统有许多相同的地方，在计算指令角速度的时候略有不同。 1)以格网坐标 G为导航坐标系，则姿态更新微分方程为 K G ： _ ： ——=========二二二二二 COS Lsin‘A ~／l 一 ‘- _ o g G = - sin tr ] = [≤

第 2期周琪等：极区飞行格网惯性导航算法原理【10，11 j。 2)速度微分方程在指北和游移方位惯导力学编排中通过积分位置方向余弦矩阵微分方程求解位置方向余弦矩阵的类比文献 [9一l3]中的比力方程可直接写出 G 方式计算飞机的当前经纬度。同样在格网惯性导航系下的速度微分方程如下。：c 一(2∞ + )×l，。+g (25) 中亦可采用该种方式计算位置，但在高纬度地区同样存在从位置方向余弦矩阵提取位置信息的难题。 g。= [0 0 一g] (26) 所以在格网惯性导航中放弃该思路而采用 ECEF坐 3)位置微分方程标表示飞机的位置 =里璺墨曼翌竺璺 — ． sinL _= 丽 v／i 丽、 =五二曼：呈墨曼墨、 = 丽 0 cosAcosL (27) ,／—1 C—OS Ls—in 一 A 由地球坐标和直角坐标间关系 r ： RNhcosLcosA 为分析格网惯性导航的性能，同时也为了方便 {Y：R cosLsinA L =[RⅣ(1一e )+h]sinL 格网惯性导航系统同其他导航系统构成组合导航系 (28) 吣 L C S n 刚 cIj S O 0 ∞ 统，有必要研究格网惯性导航的误差方程。惯性导可得所以 +y2= (R胍cosL) (29) 航的误差方程一般有两种表达形式，而两种误差方程是等效的，此处仅给出基于小扰动误差分析的误差方程。为简化分析，在推导格网导航误差方程的过程中假设地球是圆球模型。 cos (30) 记格网导航坐标下的速度误差为 61， = [6 ， Si儿 √卜 R (31) ^√ ‘ sin 去寺 (3a) (33) 焘 cos 其中 (31)式中当 L为北半球时 sinL取正号，南半球时 sinL取负号。由上述各式可以看出经度 A可以通过 (32)式和 (33)式直接求解，但是纬度 L不可直接解析求解。关于纬度的求解方法前人曾做过许多研究，亦有学者给出的闭环求解形式，但从计算精度和计算量的角度综合考虑，可参考文献 [18]两种近似求解算法。， ]T，平台失准角为 = [咖，咖，咖 ] ，直角坐标下的位置误差为 8R =[8x，8y，8z] 。，则格网惯性导航的误差方程为 = ×咖。+[’， ×c 一(2 ：+∞ ×]8v + l， ×(C,o锄 +2c ) +c V (34) G = 一 (n’ GG×)咖G+c 6'，G+ (G +c ) 一c 6R =C 6 “一C (1，“×)CR6足式中 0 一 1 0 (35) (36) C 函 1 R ．．．．．．． — — 0 0 (37) 3 格网导航误差方程。一。 c 。

· 214· 西北工业大学学报第 31卷 r2cos LsinLsinAcosA —sinL[c0s。A+sin。A(sin。L—cos。 )] sin LcosLsinA 1 一sinLcosLcosA l I sin L 0 (38) L — sinLcosLcosA — sinLcosLsinA COS L j r YGscosLcosA VGNCOSLsinA GⅣsinL ] 爿燕篱 1 L —二_ j 万一 c √ 一c。 L nA —二_ j — j (39) C月 = sinL _= 丽 sinAcosacOS2L 、 = 丽 cos sinLsinA O v／i 丽 0 二曼璺旦曼 ,／1一c0s Lsin A 二璺曼里曼墨 ,／1一c0s Lsin A COS2LsinAcosA 1 一 cos Lsin2A (40) 其中在 G 和翎的推导过程中由于格网导航在点 [83。N 108。E 5 000 m]，沿着 108。经线以 250 5 高纬度地区工作，cosL的高次方项为小量，为简化分 m／s速度向极点飞行，飞越极点后沿着 72。w 飞离析忽略了 COS L和 COS ￡相关项。 4 仿真分析为验证极区格网导航算法的合理性，生成一条特殊的轨迹，沿着某条固定的经线穿越极点然后飞出极区。由于轨迹特殊，生成的轨迹和陀螺加表信息可通过解析法给出，避免数值求解引起的计算误差。在仿真的过程中仿真参数设置如下：轨迹起始极点，飞行时间 7 200 s共 966 nm。整个飞行过程飞机保持平飞，无航向机动。对仿真数据采用设计的格网导航编排方案进行仿真。仿真过程中的算法误差如图 2～图 5所示。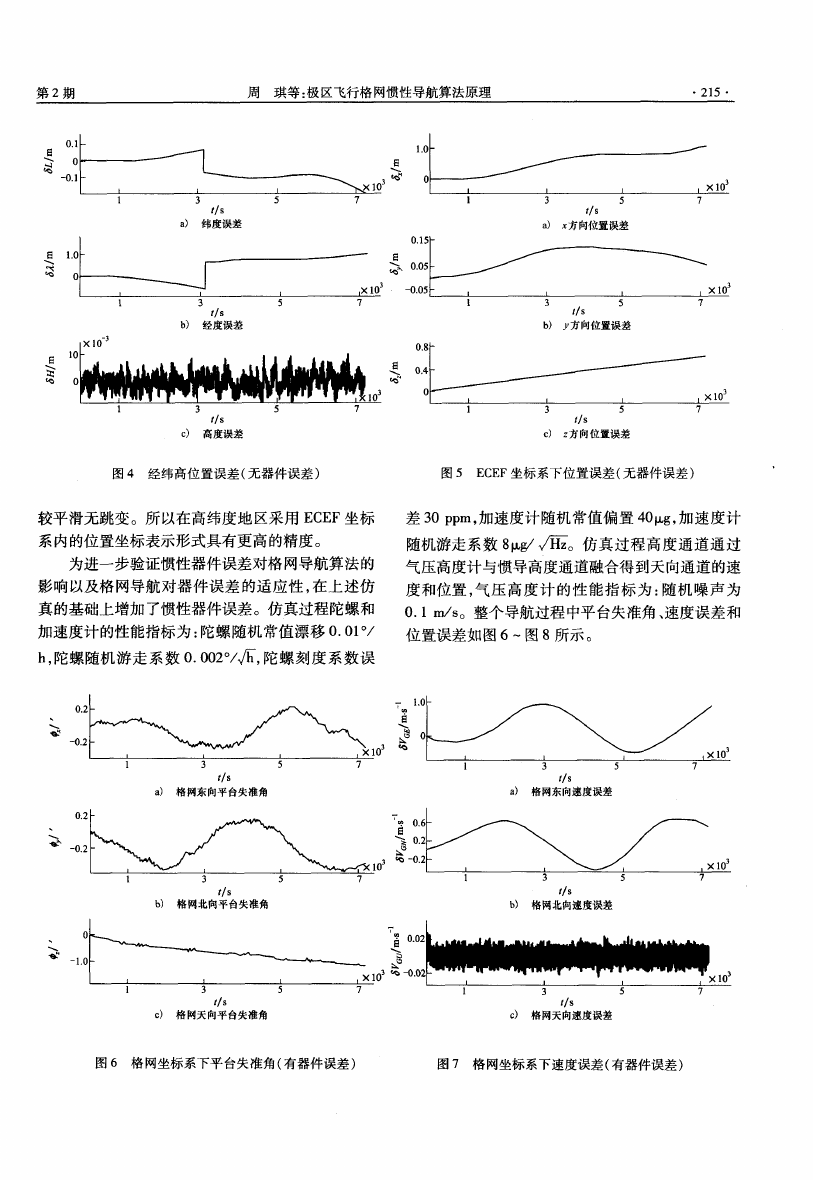由无器件误差时格网导航算法误差图可以看出格网导航在极区的算法误差很小，可以满足极区导航的需要。图 4和图 5分别比较了以经纬度表示的位置误差和 ECEF坐标系下位置误差。由图可以看出，经纬度表示的误差在过极点的时刻有明显的跳变误差，而用 ECEF坐标系表示的位置误差变化比 3 5 t／s a) 格网东向速度误差 3 5 t／s b) 格网北向速度误差 t／s c) 格网天向平台失准角 t c) 格网天向速度误差图 2 格网坐标系下平台失准角 (无器件误差 ) 图 3 格网坐标系下速度误差 (无器件误差 )

目f1 O O J O J 第 2期周琪等：极区飞行格网惯性导航算法原理 g 1 ＼ g 10 。 3 f／ 5 a) 纬度误差 3 f／s 5 b) 经度误差 3 t／s C) 高度误差 5 吕＼ O 曼 0 3 5 t／s a) x方向位置误差 3 5 t／s b) Y方向位置误差 3 5 t／s c) ：方向位置误差图 4 经纬高位置误差(无器件误差 ) 图 5 ECEF坐标系下位置误差(无器件误差 ) 较平滑无跳变。所以在高纬度地区采用 ECEF坐标差 30 ppm，加速度计随机常值偏置 40~xg，加速度计系内的位置坐标表示形式具有更高的精度。为进一步验证惯性器件误差对格网导航算法的随机游走系数 8 g／~，／Hz。仿真过程高度通道通过气压高度计与惯导高度通道融合得到天向通道的速影响以及格网导航对器件误差的适应性，在上述仿度和位置，气压高度计的性能指标为：随机噪声为真的基础上增加了惯性器件误差。仿真过程陀螺和 0．1 m／s。整个导航过程中平台失准角、速度误差和加速度计的性能指标为：陀螺随机常值漂移 0．01。／位置误差如图 6一图 8所示。 h，陀螺随机游走系数 0．002。／A ，陀螺刻度系数误 O．2 、 - 0．2 0．2 、一 0．2 、＼ 0 一 1．0 下 l 皇 03 吣 3 5 t／s 格网东向平台失准角 3 5 t／s a) 格网东向速度误差 3 f／s 5 格网北向平台失准角 3 5 t|s b) 格网北向速度误差；0 03 -o 3 t|s 5 格网天向平台失准角 3 5 f／s c) 格网天向速度误差图 6 格网坐标系下平台失准角 (有器件误差 ) 图 7 格网坐标系下速度误差 (有器件误差 )

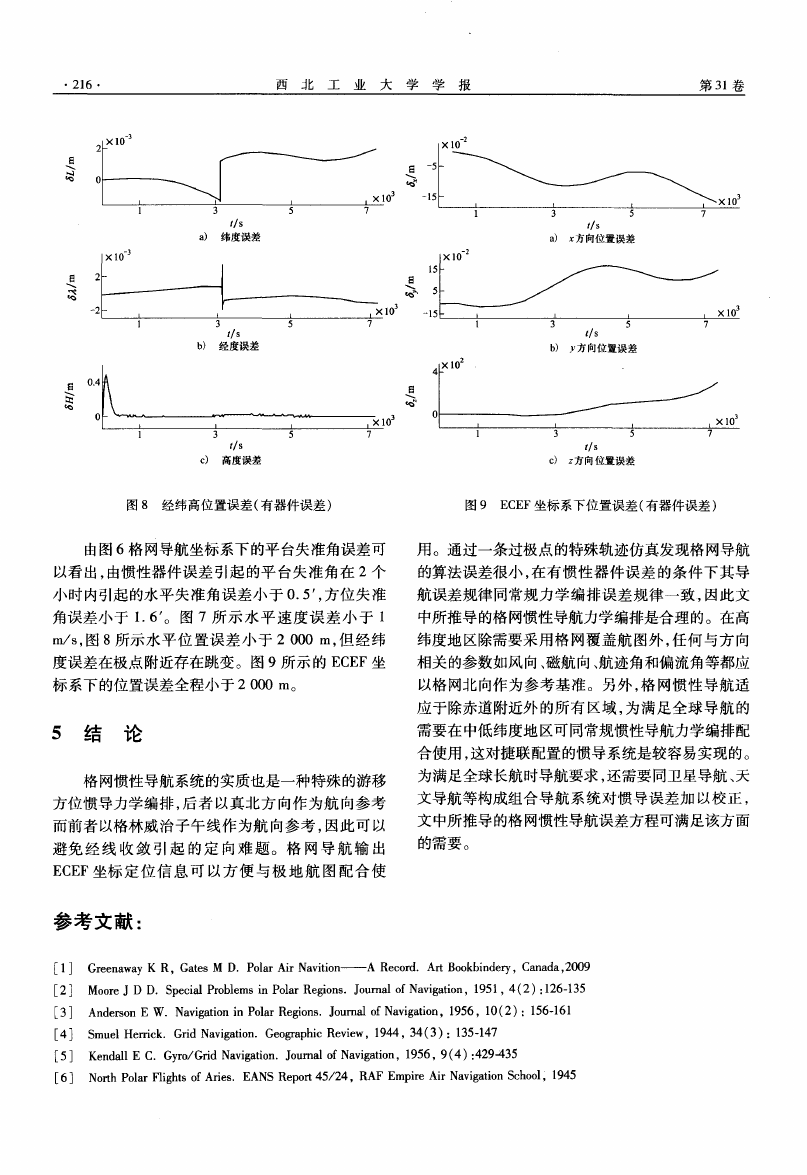
西北工业大学学报第 3l卷 g 吕 0．4 0 g 一5 03 -15 4 03 0 3 5 t／s a) 纬度误差 3 t／s b) 经度误差 5 ＼ 5 5 5 3 5 t／s c) 高度误差 3 5 t／s a) 方向位置误差 3 5 t／s b) y方向位置误差 3 5 t／s c) z方向位置误差图 8 经纬高位置误差(有器件误差) 图 9 ECEF坐标系下位置误差 (有器件误差 ) 由图 6格网导航坐标系下的平台失准角误差可用。通过一条过极点的特殊轨迹仿真发现格网导航以看出，由惯性器件误差引起的平台失准角在 2个的算法误差很小，在有惯性器件误差的条件下其导小时内引起的水平失准角误差小于 0．5 ，方位失准航误差规律同常规力学编排误差规律一致，因此文角误差小于 I．6 。图 7所示水平速度误差小于 i 中所推导的格网惯性导航力学编排是合理的。在高 m／s，图 8所示水平位置误差小于 2 000 m，但经纬纬度地区除需要采用格网覆盖航图外，任何与方向度误差在极点附近存在跳变。图 9所示的 ECEF坐相关的参数如风向、磁航向、航迹角和偏流角等都应标系下的位置误差全程小于 2 000 m。以格网北向作为参考基准。另外，格网惯性导航适 5 结论格网惯性导航系统的实质也是一种特殊的游移方位惯导力学编排，后者以真北方向作为航向参考而前者以格林威治子午线作为航向参考，因此可以应于除赤道附近外的所有区域，为满足全球导航的需要在中低纬度地区可同常规惯性导航力学编排配合使用，这对捷联配置的惯导系统是较容易实现的。为满足全球长航时导航要求，还需要同卫星导航、天文导航等构成组合导航系统对惯导误差加以校正，文中所推导的格网惯性导航误差方程可满足该方面避免经线收敛引起的定向难题。格网导航输出的需要。 ECEF坐标定位信息可以方便与极地航图配合使参考文献： f 1 1 Greenaway K R，Gates M D．Polar Air Naviti0n— — A Record．Art Bookbindery，Canada，2009 『21 Moore J D D．Special Problems in Polar Regions．Journal of Navigation，1951，4(2)：126—135 『3] Anderson E W．Navigation in Polar Regions．Journal of Navigation，1956，10(2)：156-161 『4] Smuel Herrick．Grid Navigation．Geographic Review，1944，34(3)：135-147 f5] Kendall E C．Gyro／Grid Navigation．Joumal of Navigation，1956，9(4)：429-435 『6] North Po1ar Flishts of Aries．EANS Report 45／24，RAF Empire Air Navigation School，1945

第 2期周琪等：极区飞行格网惯性导航算法原理 ·2l7· 7] 8] 9] Waldo K Lyon．The Navigation of Arctic Polar Submarines．Journal of Navigation，1984，37(2)：155-179 Le Bouar M．Navigational Equipment in the Supersonic Concorde in 1970．Journal of Navigation，1966，20(4)：490-496 Charles Broxmeyer． Inerti~ Navigation Systems．New York：McGraw Hill，1964 1O 秦永元．惯性导航．北京：科学出版社，2006 Qin Yongyuan．Inertial Navigation．BeiJing：Science Press，2006 (in Chinese) Paul G．Savage．Strapdown Analytic．Minnesota：Strapdown Associates，Inc，2000 Myron Kayton，W alter R．Fried．Avionics Navigation Systems．New York：John W iley，1996 Esmat Berkir．Introduction to Modem Navigation Systems．New Jersey：World Scientific，2007 G．Del Core．V．Nascro．A World．Wide Mechanization in Ine~ial Navigation Systems．Journal of Navigation，1986，39(3) 441．445 5 Fox W A W．Transverse Nav ation— — An Alternative to the Grid System．Journal of Navigation，1949，2(1)：25—35 6 Dyer G C．Polar Navigation— — A New Transverse Mercator Technique．Joumal of Navigation，1971，24(4)：484-495 7 Ignagni M B．All—Each Inertial Navigation Scheme．Navigation，1972，19(3)：209-214 8 Jay Farrell，Matthew Barth．The Global Positioning System and Inertial Navigation．The McGraw—Hill Companies，Inc，1999 G rid M echanization in Inertial Navigation System s for Transpolar Aircraft Zhou Qi ，Qin Yongyuan ，Fu Qiangwen ，Yue Yazhou ，1．Department of Automatic Control，Northwestern Polytechnical University。Xi an 710072，China＼＼2．Flight Automtic Control Research Institue，Xi an 710065．China ／ Abstract：The convergence of geographic meridians at the poles makes steering and positioning extremely diffi cult if not impossible when utilizing conventional inertial navigation systems(INS)during high latitude flights．The grid CO— ordinate frame mechanization of the inertial navigation system is presented to cope with above problems． The ap— proach allows grid heading to be known directly，without reference to any external sources of information． The Earth—centered Earth—fixed(ECEF)coordinates can be directly applicable to aircraft positioning in the polar regions as an alternative to the use of longitude—latitude coordinates．The grid frame mechanization error equations are de— rived for integrated navigation systems．The simulation results and their analysis show preliminarily that the error characteristics for grid frame navigation proceed in exactly the same fashion as for the conventional navigation mech- anization．The grid frame inertial navigation offers the solution to transpolar aircraft． Key words：aircraft，algorithms，computer simulation，errors， inertial navigation systems； error equation，grid navigation， polar navigation

资料库

极区飞行格网惯性导航算法原理.pdf

相关推荐

课程资源

热门标签

最新资料