PROSAC论文翻译.pdf-资料库

PROSAC 匹配-随机样本一致性摘要提出一种新的鲁棒匹配方法。随机样本一致性（PROSAC）算法通过建立临时对应关系中使用的相似性函数来利用在一组对应关系上定义的线性排序。与 RANSAC 不同，它将所有对应关系平等对待，并从整套集合中均匀地抽取随机样本，PROSAC 样本来自逐渐增加的排序最高的对应关系集。在一般的假设下，相似性度量比随机猜测能够更好地预测匹配的正确性，我们证明了 PROSAC 可以节省大量的计算量。实验证明，它经常比 RANSAC 快得多（高达一百倍以上）。对于已抽取的对应关系集的导出大小作为已抽取样本数的函数，PROSAC 在最坏的情况下接近于 RANSAC。该方法的强大功能在宽基线匹配问题上得到验证。第一节介绍在两幅或多幅图像中找到可靠的对应关系是许多计算机视觉问题中的困难和关键步骤，例如窄基线和宽基线立体匹配[6][7][10][11][17]结构和运动估计[8][14]，图像检索和对象识别[12]。通常认为，在只比较局部图像描述符的匹配过程的第一阶段，不能避免错误的匹配。由于诸如遮挡，深度不连续性和重复模式之类的现象而导致的不匹配通过用于搜索与全局约束一致的匹配组的强健方法来检测和移除。随机样本一致性 RANSAC[3]和类似的鲁棒假设和验证方法[14][15]已成为移除异常匹配的首选方法。标准 RANSAC 不在本地匹配过程建模。它被视为一个产生 N 个暂定对应关系的黑盒子，即通过比较局部描述符建立的容易出错的匹配。试探性对应的集合 U 包含一个先验未知数 I 的正确匹配（内部）。内点与通过将模型拟合到随机选择的 U 子集中找到的全局几何模型一致。当找到优秀解决方案的概率低于预选阈值时，假设-测试循环终止。RANSAC 的时间复杂度取决于 N、I 以

及几何模型的复杂度 m。绘制的平均样本数与成正比[4]。在本文中，我们介绍一种称为 PROSAC（渐进式样本一致性）的新的假设与验证（抽样与测试）匹配方法。通过利用 U 的线性排序结构，该方法实现了很大的计算节省（与 RANSAC 相比，加速因子为的数量级）。该排序至少隐式地定义在所有常用的局部匹配方法中，因为该组暂定对应性是通过首先评估随后被阈值化以获得 N 的实值相似度函数（或“质量”）而获得的对应。关于兴趣点[18]，不变描述符的马氏距离[17]或第一到第二最近邻居[5]的 SIFT 空间中的距离的比率的相关性是的常用示例。图 1 具有遮挡的长城图像对。给定 250 个暂定匹配作为输入，PROSAC 和 RANSAC 都找到了 57 个正确的对应信息（内部信息）。为了估计对极几何，RANSAC 在 10.76 秒内测试了 106,534 个七元组的对应关系，而 PROSAC 0.06 秒内测试了 9 个七元组（平均超过 100 次）。内点匹配由连接相应点的线段标记。在 PROSAC 中，样本是从逐渐增大的暂定对应中半随机抽取的。效率的提高取决于一个一般的假设，即具有高相似性的临时对应更可能是内点。更确切地说，我们假设在形成暂定匹配过程中使用的相似性所定义的顺序并不比随机排序更差。在我们的实验中，对于所有质量函数和所有测试图像对，该假设都是有效的。在第 3 节中提出的实验证明，前 n 个排序对应关系中的内点分数下降地相当快，因此 PROSAC 比最坏情况预测快了几个数量级。 (/)mNI210()q()q

PROSAC 程序原则上很简单，但要充分说明它，必须解决两个问题。首先，增长函数必须选择定义在 t 个试验后采样的 n 个排序对应的集合。其次，必须找到一个截止标准，给出与 RANSAC 类似的有关所获解决方案最优性的保证。我们提出了一个增长函数 g(t)，保证 PROSAC 至少有同样的可能性找到 RANSAC 的最优解。但是，我们还没有能够从分析的角度证明 PROSAC 和 RANSAC 在最糟糕的情况下，即随机排列对应关系时具有相同的性能。尽管如此，PROSAC 和 RANSAC 对随机排列的对应关系的比较表明，它们的表现实际上是相同的。 PROSAC 算法还有其他两个令人满意的功能。这组假设对应关系的大小 N 对其速度的影响有限，因为解决方案通常在较小的一组样本中找到时较早找到。因此有效地消除了匹配过程的一个参数。相反，用户通过指定 PROSAC 和 RANSAC 的采样分布相同的时间来控制 PROSAC 的行为。对于根据上述标准选择的增长函数，可以将 PROSAC 解释为针对所有，并行运行 RANSAC 处理的处理。在第 3 节中提出的实验中，PROSAC 的速度接近于 RANSAC 的速度，该速度将以最高内点比例的对应关系进行操作。相关工作：Tordoff 和 Murray[14]将 MLESAC[15]算法与对应的非均匀（指导）采样相结合。这是最接近 PROSAC 的已发表的工作，在两个重要方面有所不同。首先，有导向的抽样需要估计个体对应关系正确的概率，而在这里我们只假定与概率单调相关的某个量是可用的。其次，PROSAC 动态地将采样策略与采样过程本身揭示的信息相适应。假设和验证循环是一系列不正确的猜测，直到第一次成功。每次失败都会降低用于估计模型参数的对应关系正确的可能性。逐渐地，观察到的先验优先信函的证据应该会导致他们的偏好减少。PROSAC 可以被看作是一个过程的实例，首先确定性地测试最有希望的假设，然后收敛到统一的抽样，因为先验分类的“质量”的置信度在不成功的测试后下降。 PROSAC 的目标是在尽可能最短的时间内在中所有暂定匹配中找到内点，并以一定的概率保证找到所有来自的所有内点。由于这些问题与有效采样问题没有直接关系，因此不讨论与从内点集计算的模型精度有关的问题。捆绑调整[16]可以事后进行。 ()ngt=nU()gtnU()nmNNUNU

1.1 注释 N 个数据点（暂定对应）的集合表示为。中的数据点按质量函数 q 降序排列。一组具有最高质量的 n 个数据点表示为。样本 M 是数据点 , 的子集。其中 m 是样本的大小（基数）。样本的质量函数被定义为样本中包含的数据点的最低质量。第二节算法 PROSAC 算法的结构与 RANSAC 相似。首先，通过随机抽样产生假设。与 RANSAC 不同，抽样不是从所有数据中抽取，而是从具有最高质量的数据子集中抽取。假设生成集的大小逐渐增加。因此更可能未被污染的样本因此被早期检查。事实上，PROSAC 的设计与 RANSAC 相同，只是采用不同的顺序。假设是针对所有数据进行验证的。和 RANSAC 一样，当存在的解决方案比迄今为止最好的解决方案的可能性变低（小于 5％）时，该算法终止。下面讨论两个重要问题，即假设生成集的大小的选择和取样过程的终止标准。 2.1 增长函数和抽样定义的增长函数的设计必须在过分乐观地依赖于质量预先分配和过分悲观的 RANSAC 方法之间找到平衡，这种方法对所有的点对平等。如果知道概率 {对应是正确的}，那么原则上可以采用贝叶斯方法。在每个样本和测试周期之后，将对包含在样本中的所有对应关系重新计算后验概率。对应关系将按照它们的后验概率进行排序，并绘制最高概率的样本。我们推行这一研究，但放弃它有两个原因。首先，测试的对应关系的概率在测试后不是独立的，并且除了最简单的模型之外不可能表示所有的联合概率。其次，的估计中 NUNU,:()()ijNijuuUijququNUNMU||Mm=()min()iiuMqMqu=NUiPuP=iuiPuiPu

的误差通过贝叶斯公式传播并且被突出。因此，如果基于对应的相似度的的初始估计是不正确的，则后验概率很快就变得毫无价值。这里追求的另一种方法是对和相似函数之间的关联做出最小假设。特别是，我们假设单调性，即： (1) 对应的序列满足： (2) 将被称为不差于随机。我们正在寻找单一的增长功能。似乎有可能调整增长函数以反映先前的样本和测试周期的结果。然而，所有 PROSAC（和 RANSAC）的运行都是相似的：由于全部内点样本而导致的一系列失败，然后才是“命中”。采样过程的历史因此完全被 t，即到目前为止进行的测试的数量所捕获。采样策略：想象一下，标准 RANSAC 从 N 个数据点中抽取大小为 m 的样本。假设表示由 RANSAC 统一的样本的序列，并且令是根据样本质量以降序排序的相同样本的序列。如果按照的顺序进行取样，那么更有可能未被污染的样品被提前取样。逐步绘制包含质量较低的数据点的样本。在样本之后，确切地绘制了所有 RANSAC 样本。令是来自的平均样本数，其仅包含来自的数据点：然后最后，的递归关系是： iPuiPu()jqu()()ijijququPuPuijijPuPuNT1NTiiM=iNMU1NTiiM=()()()()ijijqMqM()iMNT1NTiiM=nT1NTiiM=nU10mnNNinmniTTTNNim−=−==−11100111mmnNiinNTTniNinTTNininm−−+==+−−+==−−+−1nT+

(3) 有只包含来自和的数据点的样本仅包含来自的数据点。由于，所以存在包含画出的数据点和 m-1 个数据点的 - 个样本。因此，对于，随机抽取由的数据点和 m-1 个数据点组成的 - 样本的过程有效地生成样本。由于的值一般不是整数，所以我们定义和： (4) 增长函数被定义为： (5) 在 PROSAC 中，第 t 个样本组成： (6) 是一组| 随机从中抽取的数据点。参数在多少个样本之后定义 PROSAC 和 RANSAC 的行为变得相同。在我们的实验中，参数设置为 = 200000。重复直到找到满足等式(12),(9)的解决方案。 1. 假设生成集的选择如果且，则（参见等式 4） 2. 大小为 m 的半随机样本如果，那么样本中包含从随机选择的 m-1 个点和，否则从中随机选择 m 个点。 3. 模型参数估计计算样本的模型参数。 4. 模型验证用参数查找模型的支持（即一致的数据点），根据 2.2 节选择终端长度。 111nnnTTnm++=+−nU1nT+nT1nU+11nnnUUu++=nU1nu+1nT+nTnmN=nU1nu+1nT+nT()iMnT1mT=11nnnnTTTT++=+−()min:ngtnTt=()tgttMuM=()1tgtMU−||1tMm=−()1gtU−NTNT*:0,:,:tnmnN===:1tt=+()ntT=*()nn:1nn=+tMnTt1nU−nunUtMtptp*n

算法 1：PROSAC 算法的概述。 2.2 停止标准如果集合内的内点数量满足以下条件，PROSAC 算法终止：（1）非随机性- 不在数据点集中概率是内点到任意不正确的模型的概率，小于（通常设置为 5％）。（2）极大性-一个解决方案有超过个内点在中并且在 k 个样本之后还没找到的概率不大于（通常设置为 5％）。从所有这些解决方案中选择导致终止的那个解决方案。非随机性要求可以防止 PROSAC 选择与偶然一致的异常值支持的解决方案。通常在标准方法中检查约束[1]。随机“内点”组的基数分布是二项式的。（7）其中是概率，即由包含异常值的随机样本计算出的不正确模型由样本中未包含的对应关系支持。我们基于几何考虑而粗略地设定。如果需要，PROSAC 采样期间的估计值可以更精确。对于每个 n，计算最小内点数，使得这种支持的大小随机的概率小于。（8）在上发现非随机解决方案必须满足（9）最大限度约束条件定义需要抽取多少个样本来确保解决方案的置信度，并且是 RANSAC 的（唯一）终止标准[4]。对于假设生成集合，大小为 m 的未被污染的样本从 n 个对应集合中随机选择的概率是： nU*nI*nI*n*nI*nU0()(1)RimnimnnmPiim−−+−=−−minnIminmin:()nRnnijIjPi==*nU**minnnIInUnUInP

（10）是中的内点数，是内点的分数。在 PROSAC 的 k 个样本之后的集合上失去一组大小为的内点的概率为是（其中）：（11）为确保概率而必须绘制的样本数量低于预定义的阈值是：（12）终止长度是选择最小化服从。第三节实验针对两种不同的相似度函数测试了关于对应关系排序的不差于随机的假设。基于 SIFT 描述符[5]的匹配被用于获得 PLANT 和 MUG 实验中的暂定对应。相似性被定义为最佳和第二次匹配的 SIFT 空间中距离的比率。如[5]中所述，相似性阈值设置为 0.8。这个设置已经在实验中显示出来[5][13]，以在临时对应中提供很大一部分内点。但是，这个阈值也会导致尝试性对应的绝对数量很小。在长城实验中，前 15 个离散余弦变换（DCT）系数的欧几里得距离被用作相似度函数[2][9]。DCT 是在归一化仿射不变检测平行四边形上计算的。作为暂定的对应关系，选择了具有相互最佳相似性的点。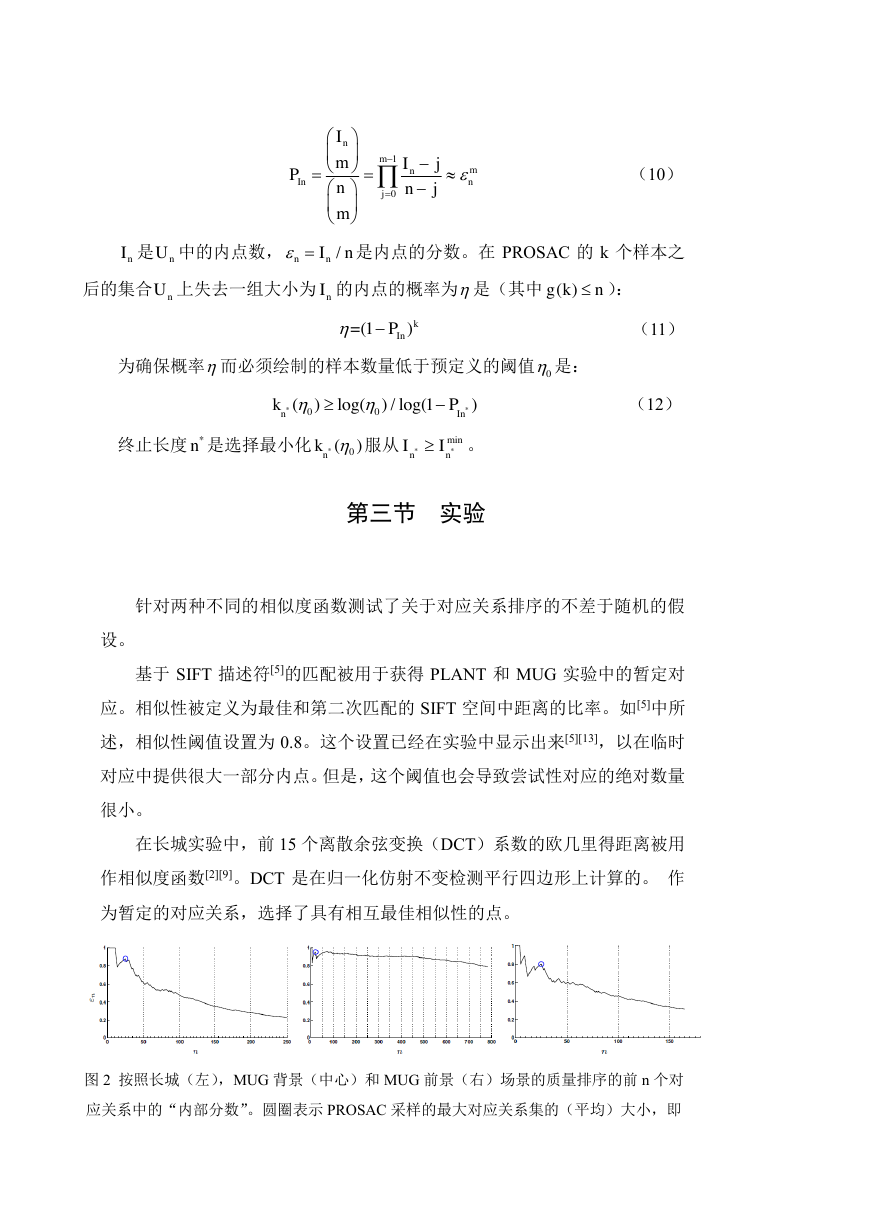图 2 按照长城（左），MUG 背景（中心）和 MUG 前景（右）场景的质量排序的前 n 个对应关系中的“内部分数”。圆圈表示 PROSAC 采样的最大对应关系集的（平均）大小，即 10nmmnInnjImIjPnnjm−=−==−nInU/nnIn=nUnI()gkn=(1)kInP−0**00()log()/log(1)nInkP−*n*0()nk**minnnII

资料库

PROSAC论文翻译.pdf

相关推荐

行业

热门标签

最新资料