铅酸蓄电池等效电路模型研究 焦 剑 1，李军徽 2，朱 昱 1，刘宏哲 1 （1. 东北电力大学 吉林省 吉林市 132012；2. 华北电力大学 电气与电子工程学院 北京市 102206） 摘 要：铅酸蓄电池在电力系统中被广泛应用，等效电路 模型是研究和应用铅酸蓄电池的重要工具。本文介绍了几 种不同的等效电路模型，在此基础上对三阶动态模型进行 了仿真研究。仿真结果表明该模型可以准确的描述铅酸蓄 电池充放电动态特性，模型中得到的端电压、荷电状态、 电解液温度等状态量为电池的应用和监测提供了依据。 二氧化铅（PbO2）为正极活性物，铅（Pb）为负 极活性物。当铅酸蓄电池放电时，在正负极板间 的电位差作用下，负极板上的电子经负载进入正 极板形成电流，电池持续向外放电；电解液中存 在的氢离子和硫酸根离子分别移向电池的正负 极，在电池内部形成电流，形成整个导电回路。 充电是放电的反过程，外接电源的正极电流从电 池的正极板流入，经电解液和负极板流回外接电 源负极，同时在充电过程中，正负极板在放电时 消耗了的活性物质被还原。 关键词：铅酸蓄电池；等效电路；三阶动态模型；荷电状 态 0 引言 目前，蓄电池是世界上最流行的能源存储设 备之一，广泛应用在不同的领域。在电力系统中， 蓄电池也扮演着重要的作用，主要有：（1）蓄电 池用于不间断电源（UPS）；（2）蓄电池作为储 能装置安装在电网侧，用于补偿有功功率；（3） 蓄电池是电动汽车的主要能量来源。相比较其他 种类的蓄电池，铅酸蓄电池技术成熟且性能良好， 体现在其制造工艺成熟、运行安全、价廉，动力 性价比高，实际应用效率较高，目前仍是最重要 和最广泛使用的二次电池。 ¨ H 铅酸蓄电池充放电时的化学反应式如下所示： Pb - Pb HSO 4 - HSO H 4 - ® 2. 充电电极反应式： 1. 放电电极反应式： + - ® H O + 2 e 2 + ® + + - Pb HSO 4 图 1 铅酸蓄电池工作原理结构图 e 2 + ® + PbSO H PbSO 2 4 PbSO H + + - PbO HSO 4 2 PbSO 4 2 H O 2 O 2 + + 2 e + 3 H + - e 2 - - 4 + 4 3 - + + 铅酸蓄电池充放电是电能与化学能转换的过 程，是一个复杂的并且对环境和电池状态敏感的 电化学反应过程。常见的电池模型包括电化学模 型、“黑箱”模型、自适应结构模型等。在电气工 程领域，更希望采用常见的电气元件，建立足够 精确的等效电路模型，准确描述铅酸蓄电池的充 放电过程。相比较实验室实验，利用仿真模型模 拟电池在不同条件下的动态特性更加方便经济。 本文介绍了铅酸蓄电池的工作原理，并且介 绍了几种不同的等效电路模型，对它们的优缺点 进行了简单的分析。着重介绍了一种铅酸蓄电池 三阶动态模型，分析了其数学模型的物理含义， 并且根据三阶动态模型，对铅酸蓄电池进行了建 模仿真，通过典型的充放电仿真结果对所建立的 三阶动态模型的准确性和有效性进行了验证。 1 铅酸蓄电池原理 2 铅酸蓄电池等效电路模型 2.1 初等电池模型[1] 初等模型如图 2 所示，是最简单的电池模型。 图中理想电压源 E0 作为电池的开路电压，定值内 阻 r 代表电池内部电阻。该模型没有考虑内阻随 电池荷电状态变化的特点，只适用于电池荷电状 态不重要的电路中。 铅酸蓄电池典型的结构如图（1）所示，包括 电解质和正负两极，电解质采用硫酸（H2SO4）， 图 2 初等电池模型 

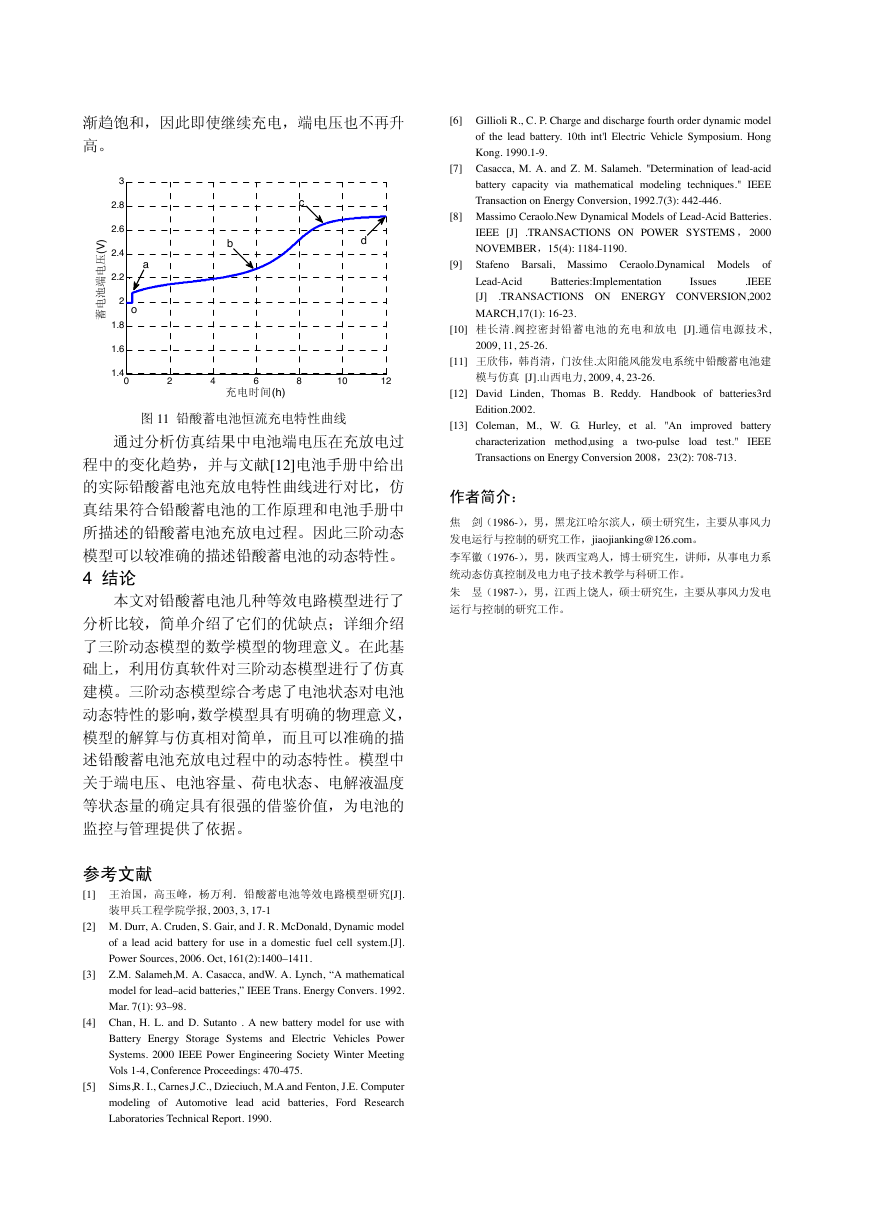
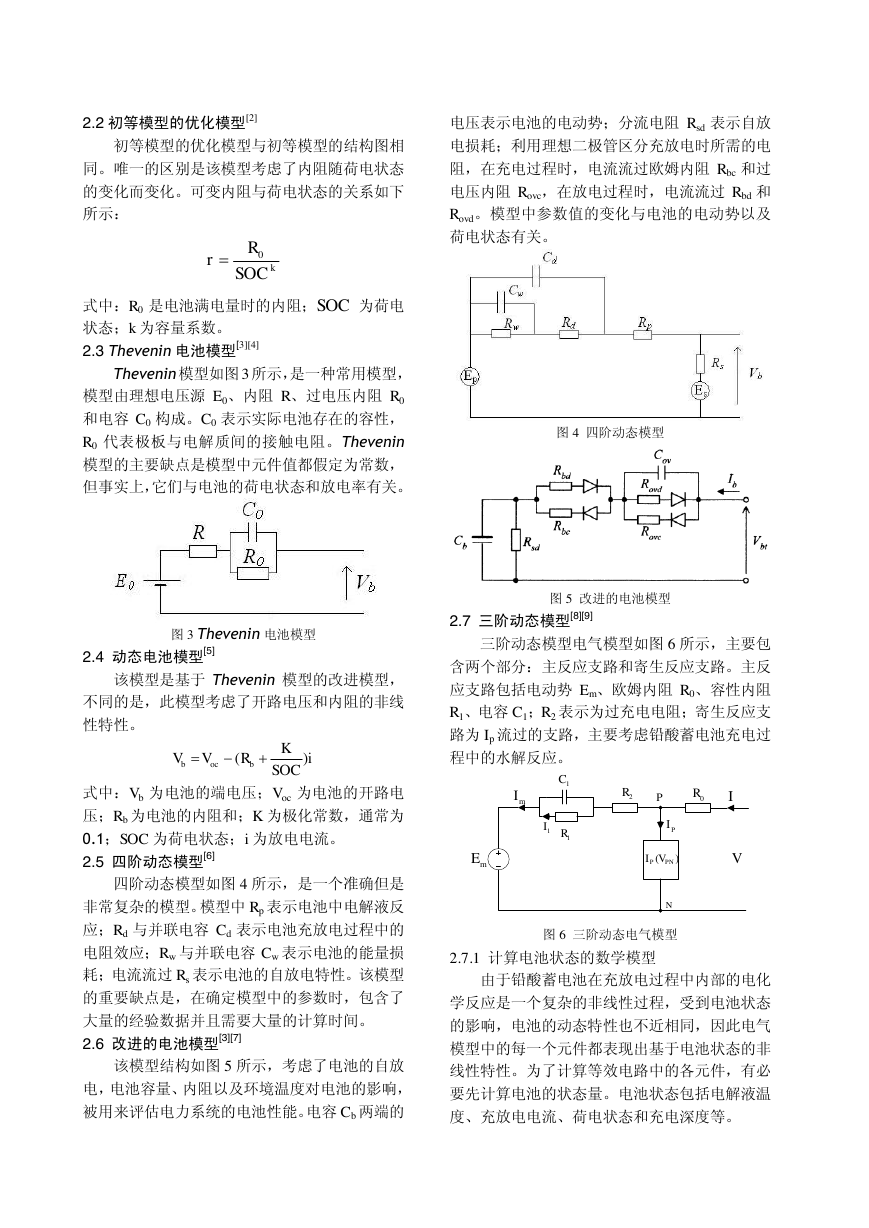
电压表示电池的电动势；分流电阻 Rsd 表示自放 电损耗；利用理想二极管区分充放电时所需的电 阻，在充电过程时，电流流过欧姆内阻 Rbc 和过 电压内阻 Rovc，在放电过程时，电流流过 Rbd 和 Rovd。模型中参数值的变化与电池的电动势以及 荷电状态有关。 图 4 四阶动态模型 2.7 三阶动态模型[8][9] 图 5 改进的电池模型 2.2 初等模型的优化模型[2] 初等模型的优化模型与初等模型的结构图相 同。唯一的区别是该模型考虑了内阻随荷电状态 的变化而变化。可变内阻与荷电状态的关系如下 所示： r = R 0 SOC k 式中：R0 是电池满电量时的内阻；SOC 为荷电 状态；k 为容量系数。 2.3 Thevenin 电池模型[3][4] Thevenin 模型如图 3 所示，是一种常用模型， 模型由理想电压源 E0、内阻 R、过电压内阻 R0 和电容 C0 构成。C0 表示实际电池存在的容性， R0 代表极板与电解质间的接触电阻。Thevenin 模型的主要缺点是模型中元件值都假定为常数， 但事实上，它们与电池的荷电状态和放电率有关。 图 3 Thevenin 电池模型 2.4 动态电池模型[5] 该模型是基于 Thevenin 模型的改进模型， 不同的是，此模型考虑了开路电压和内阻的非线 性特性。 V b = V oc - ( R b + K SOC ) i 式中：Vb 为电池的端电压；Voc 为电池的开路电 压；Rb 为电池的内阻和；K 为极化常数，通常为 0.1；SOC 为荷电状态；i 为放电电流。 2.5 四阶动态模型[6] 四阶动态模型如图 4 所示，是一个准确但是 非常复杂的模型。模型中 Rp 表示电池中电解液反 应；Rd 与并联电容 Cd 表示电池充放电过程中的 电阻效应；Rw 与并联电容 Cw 表示电池的能量损 耗；电流流过 Rs 表示电池的自放电特性。该模型 的重要缺点是，在确定模型中的参数时，包含了 大量的经验数据并且需要大量的计算时间。 2.6 改进的电池模型[3][7] 该模型结构如图 5 所示，考虑了电池的自放 电，电池容量、内阻以及环境温度对电池的影响， 被用来评估电力系统的电池性能。电容 Cb 两端的 三阶动态模型电气模型如图 6 所示，主要包 含两个部分：主反应支路和寄生反应支路。主反 应支路包括电动势 Em、欧姆内阻 R0、容性内阻 R1、电容 C1；R2 表示为过充电电阻；寄生反应支 路为 Ip 流过的支路，主要考虑铅酸蓄电池充电过 程中的水解反应。 1C 2R 0R I mI 1I 1R mE P PI ( I V P PN ) N B f rj V 图 6 三阶动态电气模型 2.7.1 计算电池状态的数学模型 由于铅酸蓄电池在充放电过程中内部的电化 学反应是一个复杂的非线性过程，受到电池状态 的影响，电池的动态特性也不近相同，因此电气 模型中的每一个元件都表现出基于电池状态的非 线性特性。为了计算等效电路中的各元件，有必 要先计算电池的状态量。电池状态包括电解液温 度、充放电电流、荷电状态和充电深度等。 

电池在充放电过程中存在热效应，主要是源 于电池内产生的焦耳热，因此电池内部的电解液 温度q也随之发生变化。其经验公式为： q d dt = 1 C q æ ç è P s - q q a - R q ö ÷ ø （1） 式中：Rθ、Cθ 分别表示为电池的热阻与热容；θa 为环境温度；Ps 表示由于电池内阻损耗产生的热 量。Ps 的计算公式为： EMF EMF = 0 + RT F lg ) a ( H SO 2 a H O ( 2 4 ) 在电池充放电过程中，随着电池荷电状态的变化， 电解液浓度发生变化，H2SO4 与 H2O 活性值也 随之发生变化。当电池的荷电状态增加时， α(H2SO4)/ α(H2O)的比值升高，因此电池电动势 EMF 随着荷电状态 SOC 增加而升高；反之，当 荷电状态降低时，电动势 EMF 下降。因此在三 阶动态模型中，计算电池电动势的经验公式为： P s = 2 I R 0 + 2 I R m 2 + 2 I R 1 1 + I V p PN （2） E m = E m 0 - K E (273 q + )(1 - ) SOC （7） 根据电量的定义，电池输出电量的瞬时值 Qe(t)等于放电电流 Im对时间的积分加上电量初始 值。 Q t Q ( ) = e e init _ t + -ò 0 I m dt t ( ) （3） 式中：Qe_init 为电量初始值，t 为充放电时间。 电池容量定义为满电量的电池在给定电解液 温度和放电电流的条件下，放电达到规定终止电 压时电池能够释放出的电量。经验公式如下所示： ( , C I q ) = K C 0* c + 1 ( K c (1 - q q - f 1)( I / / I e ) d * ) （4） 式中：I 为电池放电电流；θ 为电解液温度；θf 为 电解液冻结温度，通常等于-40˚C ；Kc、C0*、ε、 I*、δ 为经验系数。 荷电状态（SOC）定义为电池剩余容量与在 相同条件下电池完全充满电时的容量的比值，表 示在某一时刻电池内固有容量的状态，其表达式 为： 式中：Em0 为电池满电量时的开路电压；KE 为经 验系数。 由于在电池充电过程中存在水解反应，会消 耗一部分充电能量。利用寄生反应支路的电流损 耗 IP 表示这部分能量损耗。根据塔菲尔电压电流 关系，电流 IP 与节点电压 VPN 和电解液温度有关。 I P = V G P PN 0 exp ( V PN / V P 0 + A P (1 - q q f / ) ) （8） 式中：VPN 为寄生支路节点电压； GP0、VP0、AP 为经验系数。 在三阶动态模型中，R0、R1、C1、R2 可由下 述经验公式计算： R 0 = R 00 [ 1 + A 0 (1 - SOC ) ] （9） R 1 = - 10 ln( R DOC ) （10） C 1 Rt= 1 / 1 （11） SOC = - 1 Q C q ) (0, / e （5） R 2 = R 20 [ exp A 21 + 1 exp( - (1 A I 22 ] SOC ) * ) I / m （12） 式中：C(0, θ)表示当电解液温度为 θ 时，电池充 满电，即放电电流为 0 时的容量。 充电深度（DOC）定义为电池剩余容量与在 相同条件下电池实际可用容量的比值，表示电池 在某一时刻可用电量的状态，其表达式为： 式中：R00 为满电量是的内阻；A0、R10、τ1、R20、 A21、A22 为经验系数。 在计算出上述各元件数值之后，就可以根据 欧姆定律计算出电池的端电压： DOC = - 1 Q C I q ) ( / , avg e （6） V E = + IR 0 + I R 2 m + I R 1 1 m （13） 式中：C(Iavg, θ)表示在电解液温度为 θ，电池平均 放电电流 Iavg 条件下电池能够释放出的容量。 2.7.2 计算模型中各元件的数学模型 电池电动势定义为在电池化学能与电能的转 换达到平衡时，正负两极平衡电极电势的差值， 数值上等于电池稳定时的开路电压。跟据能斯特 方程，铅酸蓄电池的电动势计算式为： 3 铅酸蓄电池三阶动态模型仿真分析 通过对上述铅酸蓄电池等效电路模型的介绍 与比较，三阶动态模型充分考虑了铅酸蓄电池充 放电过程中的非线性特性，考虑了电解液温度、 荷电状态、充电深度等状态量对电池动态特性的 影响。为了验证三阶动态模型的正确性和有效性， 利用 PSCAD/EMTDC 仿真软件对该模型进行仿 

真建模。 根据上述介绍的三阶动态模型的数学模型， 确定其输入-输出关系如图 7 所示：输入量为充放 电电流 I、环境温度 θa，输出量为电池端电压 V、 荷电状态 SOC、充电深度 DOC、电解液温度 θ。 模型在 PSCAD/EMTDC 中的仿真结构如图 8 所 示。由于寄生支路和电阻 R2 表现充电过程中的电 池特性，即在放电过程中 IP=0、R2=0。采用额定 电压 2V，容量 C10=500Ah 的铅酸蓄电池参数进行 仿真分析[8]。在环境温度不变，恒定电流充放电 的条件下，通过观察电池端电压的变化趋势验证 该模型的准确性和有效性。 模型参数 I aq 电池模型 SOC DOC V q 图 7 模型输入输出关系图 I theta_a theta_a Ps theta 热量模块 theta Im DOC SOC 电量与容量模块 theta DOC R1 计算R1 DOC SOC 5000.0 Tau1 N D N/D I R1 C1 Em R0 R2 Em RO R2 SOC theta SOC SOC Im Vpn theta 计算Em 计算R0 计算R2 计算Ip Ip Ip 等效电路模块 V V Ps Im Vpn 图 8 仿真模型结构图 3.1 恒流放电特性 在环境温度为 25℃恒定不变的情况下，将满 电量的电池从 1000s 开始以电流为 0.1C10，即 50A 恒流放电到终止电压 1.75V 后停止放电。 图 9 给出了上述条件下电池端电压随时间的 变化情况。当电池没有放电时，端电压等于满电 量时的开路电压 2.135V；放电初瞬（曲线 oa 段）， 由于电池欧姆内阻 R0 的压降在出现电流时突现， 电池端电压迅速下降；在放电中期，电极周围的 电解液浓度比较稳定，电池端电压变化曲线也呈 现平稳状态，但是由于电解液浓度仍然缓慢下降， 因此电池端电压缓慢降低，如图中曲线 ab 段的变 化趋势；放电后期如曲线 bc 段，由于大量生成的 硫酸铅阻碍外部硫酸的渗入，在等效电路中表现 为内阻大大增加，导致电池端电压迅速下降；当 放电至 c 点即电压降至终止电压时，停止放电， 电池端电压逐渐回升，最后稳定在 1.98V。 ) ( V 压 电 端 池 电 蓄 o a 2.2 2.1 2 1.9 1.8 1.7 1.6 1.5 0 2 4 b d c 10 12 14 6 8 放电时间(h) 图 9 铅酸蓄电池恒流放电特性曲线 图 10 给出了电池荷电状态的变化曲线。当电 池没有放电时，荷电状态等于 1，表示此时电池 满电量；在 ac 段电池恒流放电时，荷电状态随放 电时间线性下降，持续时间为 10h，则电池输出 电量为 500Ah，放电效率为 100%，表明铅酸蓄电 池采用 0.1C10 电流放电较为合理；当电池停止放 电时，荷电状态保持不变。 1 0.8 0.6 0.4 0.2 态 状 电 荷 池 电 蓄 0 0 2 4 6 8 10 12 14 放电时间(h) 图 10 恒流放电时的荷电状态变化曲线 3.2 恒流充电特性 恒流充电时的端电压变化特性曲线如图 11 所示。充电初始电池端电压迅速被提升，如图中 曲线 oa 段；在充电中期（曲线 ab 段），随着充电 的进行，由于极板表面和活性物质微孔中硫酸增 加的速度和向外扩散的速度趋于平衡，所以电解 液浓度不再急剧上升，因此电池端电压比较缓慢 的上升；充电后期，电流电解水产生气体，由于 气体为不良导体，使电池内阻增大，因此电池端 电压又迅速上升，变化趋势如曲线 bc 段；当充电 至 cd 段时，活性物质已全部被还原，水的分解也 

[6] Gillioli R., C. P. Charge and discharge fourth order dynamic model of the lead battery. 10th int'l Electric Vehicle Symposium. Hong Kong. 1990.1-9. [7] Casacca, M. A. and Z. M. Salameh. "Determination of lead-acid battery capacity via mathematical modeling techniques." IEEE Transaction on Energy Conversion, 1992.7(3): 442-446. [8] Massimo Ceraolo.New Dynamical Models of Lead-Acid Batteries. IEEE [J] .TRANSACTIONS ON POWER SYSTEMS ， 2000 NOVEMBER，15(4): 1184-1190. [9] Stafeno Barsali, Massimo Ceraolo.Dynamical Models of .IEEE .TRANSACTIONS ON ENERGY CONVERSION,2002 Batteries:Implementation Issues Lead-Acid [J] MARCH,17(1): 16-23. [10] 桂长清.阀控密封铅蓄电池的充电和放电 [J].通信电源技术, 2009, 11, 25-26. [11] 王欣伟，韩肖清，门汝佳.太阳能风能发电系统中铅酸蓄电池建 模与仿真 [J].山西电力, 2009, 4, 23-26. [12] David Linden, Thomas B. Reddy. Handbook of batteries3rd Edition.2002. [13] Coleman, M., W. G. Hurley, et al. "An improved battery test." IEEE characterization method,using a Transactions on Energy Conversion 2008，23(2): 708-713. two-pulse load 作者简介： 焦 剑（1986-），男，黑龙江哈尔滨人，硕士研究生，主要从事风力 发电运行与控制的研究工作，jiaojianking@126.com。 李军徽（1976-），男，陕西宝鸡人，博士研究生，讲师，从事电力系 统动态仿真控制及电力电子技术教学与科研工作。 朱 昱（1987-），男，江西上饶人，硕士研究生，主要从事风力发电 运行与控制的研究工作。 渐趋饱和，因此即使继续充电，端电压也不再升 高。 ) ( V 压 电 端 池 电 蓄 a 3 2.8 2.6 2.4 2.2 2 o 1.8 1.6 1.4 0 c b d 2 4 6 充电时间(h) 8 10 12 图 11 铅酸蓄电池恒流充电特性曲线 通过分析仿真结果中电池端电压在充放电过 程中的变化趋势，并与文献[12]电池手册中给出 的实际铅酸蓄电池充放电特性曲线进行对比，仿 真结果符合铅酸蓄电池的工作原理和电池手册中 所描述的铅酸蓄电池充放电过程。因此三阶动态 模型可以较准确的描述铅酸蓄电池的动态特性。 4 结论 本文对铅酸蓄电池几种等效电路模型进行了 分析比较，简单介绍了它们的优缺点；详细介绍 了三阶动态模型的数学模型的物理意义。在此基 础上，利用仿真软件对三阶动态模型进行了仿真 建模。三阶动态模型综合考虑了电池状态对电池 动态特性的影响，数学模型具有明确的物理意义， 模型的解算与仿真相对简单，而且可以准确的描 述铅酸蓄电池充放电过程中的动态特性。模型中 关于端电压、电池容量、荷电状态、电解液温度 等状态量的确定具有很强的借鉴价值，为电池的 监控与管理提供了依据。 参考文献 [1] 王治国，高玉峰，杨万利．铅酸蓄电池等效电路模型研究[J]. 装甲兵工程学院学报, 2003, 3, 17-1 [2] M. Durr, A. Cruden, S. Gair, and J. R. McDonald, Dynamic model of a lead acid battery for use in a domestic fuel cell system.[J]. Power Sources, 2006. Oct, 161(2):1400–1411. [3] Z.M. Salameh,M. A. Casacca, andW. A. Lynch, “A mathematical model for lead–acid batteries,” IEEE Trans. Energy Convers. 1992. Mar. 7(1): 93–98. [4] Chan, H. L. and D. Sutanto . A new battery model for use with Battery Energy Storage Systems and Electric Vehicles Power Systems. 2000 IEEE Power Engineering Society Winter Meeting Vols 1-4, Conference Proceedings: 470-475. [5] Sims,R. I., Carnes,J.C., Dzieciuch, M.A.and Fenton, J.E. Computer modeling of Automotive lead acid batteries, Ford Research Laboratories Technical Report. 1990.