logo资料库

高频电子线路 课后答案 曾兴雯.doc

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：4.39M 资料格式：doc 举报 版权申诉
第1页 / 共80页
第2页 / 共80页
第3页 / 共80页
第4页 / 共80页
第5页 / 共80页
第6页 / 共80页
第7页 / 共80页
第8页 / 共80页
资料共80页，剩余部分请下载后查看
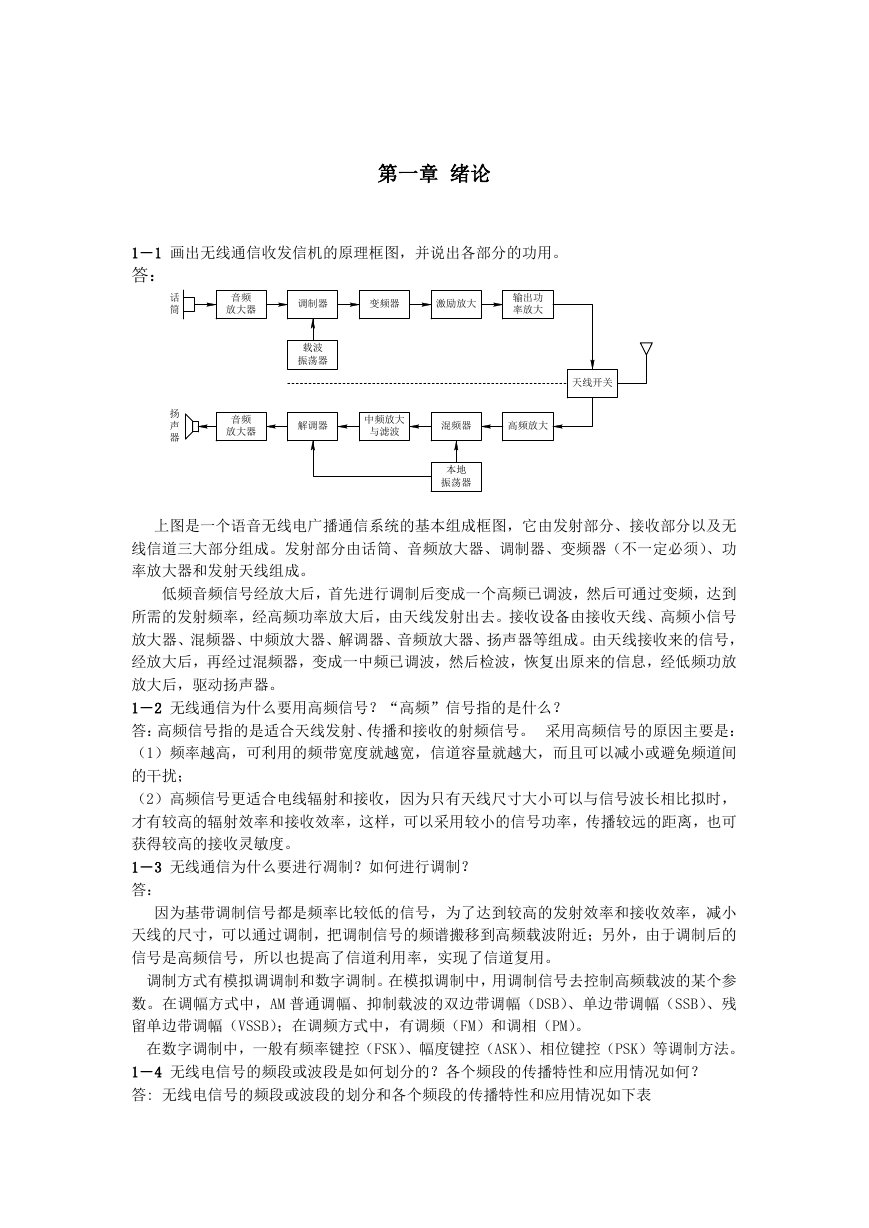
    第一章 绪论 1－1 画出无线通信收发信机的原理框图，并说出各部分的功用。 答： 话 筒 扬 声 器 音频 放大器 调制器 变频器 激励放大 输出功 率放大 载波 振荡器 天线开关 音频 放大器 解调器 中频放大 与滤波 混频器 高频放大 本地 振荡器 上图是一个语音无线电广播通信系统的基本组成框图，它由发射部分、接收部分以及无 线信道三大部分组成。发射部分由话筒、音频放大器、调制器、变频器（不一定必须）、功 率放大器和发射天线组成。 低频音频信号经放大后，首先进行调制后变成一个高频已调波，然后可通过变频，达到 所需的发射频率，经高频功率放大后，由天线发射出去。接收设备由接收天线、高频小信号 放大器、混频器、中频放大器、解调器、音频放大器、扬声器等组成。由天线接收来的信号， 经放大后，再经过混频器，变成一中频已调波，然后检波，恢复出原来的信息，经低频功放 放大后，驱动扬声器。 1－2 无线通信为什么要用高频信号？“高频”信号指的是什么？ 答：高频信号指的是适合天线发射、传播和接收的射频信号。 采用高频信号的原因主要是： （1）频率越高，可利用的频带宽度就越宽，信道容量就越大，而且可以减小或避免频道间 的干扰； （2）高频信号更适合电线辐射和接收，因为只有天线尺寸大小可以与信号波长相比拟时， 才有较高的辐射效率和接收效率，这样，可以采用较小的信号功率，传播较远的距离，也可 获得较高的接收灵敏度。 1－3 无线通信为什么要进行凋制？如何进行调制？ 答： 因为基带调制信号都是频率比较低的信号，为了达到较高的发射效率和接收效率，减小 天线的尺寸，可以通过调制，把调制信号的频谱搬移到高频载波附近；另外，由于调制后的 信号是高频信号，所以也提高了信道利用率，实现了信道复用。 调制方式有模拟调调制和数字调制。在模拟调制中，用调制信号去控制高频载波的某个参 数。在调幅方式中，AM 普通调幅、抑制载波的双边带调幅（DSB）、单边带调幅（SSB）、残 留单边带调幅（VSSB）；在调频方式中，有调频（FM）和调相（PM）。 在数字调制中，一般有频率键控（FSK）、幅度键控（ASK）、相位键控（PSK）等调制方法。 1－4 无线电信号的频段或波段是如何划分的？各个频段的传播特性和应用情况如何？ 答: 无线电信号的频段或波段的划分和各个频段的传播特性和应用情况如下表
    第二章 高频电路基础 2－1 对于收音机的中频放大器，其中心频率 f0=465 kHz．B0.707=8kHz，回路电容 C=200pF， 试计算回路电感和 QL 值。若电感线圈的 QO=100，问在回路上应并联多大的电阻才能满 足要求。 解 2-1： f 由 0 L  2 4   2 465  1 10 6  200 10   12  0.586 mH 2  200 得： 3 465 10  3 8 10   58.125 得：  2  1 LC 1  f C 2 （ ） 0 6 10 465 2 4  2    f 0 Q L  由B 0 .7 0 7  Q L  f 0 B 0.707 R 因为： 0  Q L  Q 0 C  0 C  0 g    200 10   100 3   2 465 10   C Q  0 0 R g g   0 R L 1  L 0  12 9 10 2 465 2     171.22 k  1 所以： （  R L Q 0 Q L  1 ） R 0  Q L Q Q  0 L R 0  58.125  100 58.125  171.22  237.66 k 
    答：回路电感为 0.586mH,有载品质因数为 58.125,这时需要并联 236.66kΩ的电阻。 2－2 图示为波段内调谐用的并联振荡回路，可变电容 C 的变化范围为 12～260 pF，Ct 为微调电容，要求此回路的调谐范围为 535～1605 kHz，求回路电感 L 和 Ct 的值，并要 求 C 的最大和最小值与波段的最低和最高频率对应。 题 2－2 图    根据已知条件，可以得出： C 回路总电容为  1 6 0 5 1 0     5 3 5 1 0   C C t 1 LC 1 LC 2  2  max min       3 3 , 因此可以得到以下方程组 1  1  2  L (12 10  12  C t ) 2  L (260 10  12  C t ) 1 6 0 5 5 3 5  260 10 12 10     12 12 C  C  t t ， 260 10 12 10     12 12 C  C  t t  9 8 C t  260 10   12   9 12 10   12 260 108 10  C t   12  19 pF  8 1 3 2 260 19 ）（   ）1 0 -1 2 L  2   （  535 10 1 0 6  3 1 4 9 4 2 3 4 3 5  0.3175 mH 答：电容 Ct 为 19pF，电感 L 为 0.3175mH. 2－3 图示为一电容抽头的并联振荡回路。谐振频率 f0=1MHz，C1=400 pf，C2=100 pF 求回 2
    路电感 L。若 Q0=100，RL=2kΩ，求回路有载 QL 值。 解 2-3 C  L   40000 500 2 1  C C 1 2 C C  1 f C 0 1 6 2 (2  ) 2 题 2－3 图  80 pF , (2   10 ) 80 10   0.317 mH 12  负载 接入系数为p = R L C 1  C C 1  400 500 2  0.8 折合到回路两端的负载电阻为   R L R L 2 p  2 0.64  3.125 k  回路固有谐振阻抗为R  0 有载品质因数 Q  L Q 0 R 0   R L 1  Q 0 2 f C  0 100 199  3.125 1   1.546 100 6 6.28 10   80 10    199 k  12 答：回路电感为 0.317mH,有载品质因数为 1.546 2－4 石英晶体有何特点？为什么用它制作的振荡器的频率稳定度较高？ 答 2-4： 石英晶体有以下几个特点 1. 晶体的谐振频率只与晶片的材料、尺寸、切割方式、几何形状等有关，温度系数非 常小，因此受外界温度影响很小 2. 具有很高的品质因数 3. 具有非常小的接入系数，因此手外部电路的影响很小。 4. 在工作频率附近有很大的等效电感，阻抗变化率大，因此谐振阻抗很大 5. 构成震荡器非常方便，而且由于上述特点，会使频率非常稳定。 3
    2－5 一个 5kHz 的基频石英晶体谐振器， Cq=2.4X10－2pF C0=6pF，，ro=15Ω。求此谐振器 的 Q 值和串、并联谐振频率。 解 2-5： 总电容 C  串联频率 f q  6 0.024  6 0.024  f 0 0.024 12 1       0 C q 2C 0 C C q 0 C C  q f 0   1   1 0.024pF C  q  0.998f 0  4.99kHz 品质因数 Q  2 f Cr  q 0  2    5 10 3  1 0.024 10  12   15  10 3.6 9   88464260 答：该晶体的串联和并联频率近似相等，为 5kHz，Q 值为 88464260。 2－6 电阻热噪声有何特性？如何描述 答 2-6： 电阻的热噪音是由于温度原因使电阻中的自由电子做不规则的热运动而带来的，因此热噪 音具有起伏性质，而且它具有均匀的功率谱密度，所以也是白噪音，噪音的均方值与电阻的 阻值和温度成正比。   S 噪音电压功率谱 U S 噪音电流功率谱 2－7 求如图所示并联电路的等效噪声带宽和输出均方噪声电压值。设电阻 R=10kΩ，C=200 4 kTRB  4 kTGB  噪音电压均方值 , 4 kTR 4 kTG ， 噪音电流均方值 2 E n 2 I n I pF，T=290 K。 解 2-7： 网络传输函数为 H (j )   1 j C   1 R  1  R j CR  , 则等效噪音带宽为 题 2－7 图 H 0  R df 2 ) arctan(2  fCR )  0   0 | ( H j ) |  2 df  H 2 0   0   0 1  1 (2  df fCR ) 2 1 1 ( CR   1 2 CR   B = n   1 4 CR  1 200 10   12  6 10 8 4 10  4   125 kHz 4
    输出噪音电压均方值为 U 2 n  n 4 kTGB H 2 0 4 1.37 10    1 R  kT B R n 290 10  4  23  2  4 kTRB n 4  125 10  3  19.865( 2 V ) 答：电路的等效噪声带宽为 125kHz，和输出均方噪声电压值为 19.865μV2. 2－8 如图所示噪声产生电路，已知直流电压 E=10 V，R=20 kΩ,C=100 pF，求等效噪声带 宽 B 和输出噪声电压均方值（图中二极管 V 为硅管）。 解 2-8： 此题中主要噪音来自二极管的散粒噪音，因此 题 2－8 图 流过二极管的电流为 I = 0 E -V R D  二极管电阻为  9.3 20000  R D , mA   56 0.465 26 mV I 0 网络传输函数为 1 H (j )   1 // R R  j C  D 1  j C   1  R D j CR  , D  1 R D H R  0 D 等效噪音带宽为：   0 B = n | ( H j ) |  2 df  H 2 0   0   1 2 CR  10 10 224  arctan(2  fCR ) D  0  D 44.64 MHz 1 CR  1 (  df  D 2 ) 1 4 CR  D df 2 ) D  0  1 1 (2 fCR   1 4 100 10   12  56  U 2 n 2 2 I qB H  0 0 2 0.465 10    n  3  1.6 10   19  44.64 10  6  56  2083 (  2 V  ) 2 5
    2－9 求图示的 T 型和П 型电阻网络的噪声系数。 题 2－9 图 解 2-9 设两个电路的电源内阻为 Rs 1. 解 T 型网络 输出电阻为R  0 ( ) R R R  1 3 s R R R   1 3 s  R 2 （1）采用额定功率法 P 输入匹配功率 smi  噪音系数 N  F P smi P smo （2）采用开路电压法    R s  R 3 R R  1 3 4 R 0 E s 2    P smo  2 E s 4 R s R 0 R s  ， 输出匹配功率 R s      R R 1 3 R 3 2    U 2 nio  N F     U U R s 2 no 2 nio    R 3 R R 1 3 R R 0 s R s    U 2 no  4 kTBR 0 2     4 kTBR ， s  R R 1 3 R 3 2    （3）采用短路电流法 I 2 no  4 kTB 1 R 0 R s  R 1 R R 2 3 R R  3 2 R R 3 s ) R R  1 3    R 3  R 2 R 3 2       2    R R 3 s ( R 1 )  6  R s 1 R s        1  R R R  s s        R s  ( ( 2 I 2 nio  4 kTB  4 kTB  4 kTBR s R 3 R 2  )    ( ) R R R  3 1 s R R R   1 3 s    R R 1 3  2         4 kTB R s 2 R 0    ( R s  2 R 3 R R 1 3  )   
    2.解П型网络 输出电阻为： R 0        R R 1 s R R  1 s R R 1 s R R  1 s  R R 2 3     R 2     R 3 （1）采用额定功率法   R R 1 s R R  1 s  R R R R R   2 1 3 2 s ( )( R R R R   1 3 2 s ) 2     R  3 R   3 R  2 R  2 R R 1 s R R 3 s )( R 3  R 1 ) 2       2    R 1  R s R 1 P smi P smo  R 0 R s s  R R R 0 1  R  s 1 R R 0 s    R 3 R R  1 s R R R R  1 s 1 s R R  4 R 1 s 0 R 1          (  R 2  R R 1 3 R R 2 s R 1 R R 1 s   R R 1 2 2    P 输入匹配功率 smi P 输出匹配功率 smo N 得噪音系数为 F  2 E s 4 R s         E s   （2）采用开路电压法 U 2 no  4 kTBR 0 U 2 nio  4 kTBR s  4 kTBR s             R 1  R R 1 s  R 3  R R 1 s R R  1 s R 2  R 3 2       R 1  R R 1 s   4 kTBR R s 2 0    N F  U U 2 no 2 nio  1 R R 0 s  R R 1 s  R R 1 s    R 2 2   R  0 R R  1 s  R R   1 s 2  R 1  R R R R  2 s R R R R 2 s R 1   7 2 1 1 2  2   
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料