第1页 / 共14页
第2页 / 共14页
第3页 / 共14页
第4页 / 共14页
第5页 / 共14页
第6页 / 共14页
第7页 / 共14页
第8页 / 共14页
基于直方图平移的可逆水印算法.pdf
Introduction
Reversible Watermarking Algorithm
Reversible Watermarking Algorithms Based on Data Compression
Reversible Watermarking Algorithms Based on Space Expansion
Reversible Watermarking Algorithms Based on Histograms
A New Reversible Watermarking Algorithm
Location Map
Histogram Shifting
Embedding Algorithm
Extraction and Recovery Algorithm
Algorithm Extension
Experimental Results and Analysis
Conclusions
References
A Reversible Watermarking Based on Histogram
Shifting
JinHa Hwang1, JongWeon Kim1, and JongUk Choi1,2
1 Copyright Protection Research Institute, Sangmyung University,
7, Hongji-dong, Jongno-gu, Seoul, 110-743, Korea
{auking45, jwkim, juchoi}@smu.ac.kr
http://cpri.smu.ac.kr/
2 MarkAny Inc., 10F, Ssanglim Bldg., 151-11, Ssanglim-dong,
Jung-gu, Seoul, 100-400, Korea
juchoi@markany.com
http://www.markany.com/
Abstract. In this paper, we propose a reversible watermarking algorithm where
an original image can be recovered from watermarked image data. Most water-
marking algorithms cause degradation of image quality in original digital con-
tent in the process of embedding watermark. In the proposed algorithm, the
original image can be obtained when the degradation is removed from the wa-
termarked image after extracting watermark information. In the proposed algo-
rithm, we utilize a peak point of image histogram and the location map and
modify pixel values slightly to embed data. Because the peak point of image
histogram and location map are employed in this algorithm, there is no need of
extra information transmitted to receiving side. Also, because a slight modifica-
tion on pixel values is conducted, highly imperceptibly images can be achieved.
As locations of watermark embedding are identified using location map,
amount of watermark data can dramatically increases through recursive embed-
ding. Experimental results show that it can embed 5K to 130K bits of additional
data.
1 Introduction
Development of computer technology and widespread use of internet have driven this
world into fast-changing digital place. With digitization of multimedia contents, eve-
rybody can access multimedia contents more easily than in analog age. Even if digiti-
zation of the multimedia contents provides more opportunities to media contents, it
also provide easy access paths to copy and distribution of digital contents, because of
characteristics of the digital data, represented by 0 and 1. As the copy and distribution
of digital contents are widely conducted illegally in internet environment, the copy-
right holders began to pay attention to copyright protection technologies.
Of the technologies that can protect copyright of digital contents, watermarking
technology has received keen interests from research communities. Watermarking
technology hides copyright information into original contents to protect copyright,
which eventually leads to modification of original contents. However, in order to
Y.Q. Shi and B. Jeon (Eds.): IWDW 2006, LNCS 4283, pp. 348 – 361, 2006.
© Springer-Verlag Berlin Heidelberg 2006
A Reversible Watermarking Based on Histogram Shifting
349
achieve the goal of imperceptibility, the watermarking technology modifies original
contents so that the modification is not perceptible to naked eyes using Human Visual
System (HVS) modeling. As a result, the original image cannot be recovered when
the image is watermarked. In the applications where a slight modification can lead to
significant difference in final decision making process, such as medical images or
military images systems, there has been a requirement of recovery to original con-
tents. For the reason, there have been research efforts of reversible watermark that can
recover to original images from watermarked images [2], [3].
The reversible watermark technologies that have been published can be categorized
into embedding into spatial domain [1], [2], [3], and embedding in transformation
domain [6], [8]. Of the embedding technology into spatial domain, the algorithm
suggested by Z. Ni [1] embeds watermark using maximum point and minimum point
of histogram, demonstrating excellent imperceptibility of more than 48dB. However,
even if it can achieve high degree of data embedding by embedding watermark into
maximum value points, the maximum point is changed after embedding watermark
data. A problem of this approach is that maximum point and minimum point of his-
togram should be transmitted to the receiving side for data retrieval.
In this paper, an algorithm is proposed in which additional information is not re-
quired for recovery of original image, because we embed watermark data with loca-
tion map which is composed of information of maximum point and minimum point of
the histogram. In this algorithm, by embedding recursively watermark information
using expansion of location map a reversible watermarking algorithm is suggested
that can greatly enhance amount of embedded information.
In Section 2, we describe previous research efforts in reversible watermarking area
for comparison, we explain suggested watermarking algorithm in section 3. In sec-
tion 4, we analyze experimental results of the suggested algorithm and we describe
summary of this research and future research direction in section 5.
2 Reversible Watermarking Algorithm
Reversible watermarking algorithms belongs to fragile watermarking area that has
attracted researcher’s attention in specific applications such as military data or medi-
cal imaging area. The algorithms embed fragile watermark into digital contents for the
purposes of content authentication and checking integrity of watermarked contents, or
others. The most significant advantage of the reversible watermarking algorithms is
that it can recover original contents after removing degradation caused by information
embedding after extracting watermark information. Recently many research reports
have been published, which can be mainly categorized into three methods [9].
2.1 Reversible Watermarking Algorithms Based on Data Compression
Many reversible watermarking algorithms suggested so far belong to this category that
embeds information by compressing spatial domain. A typical example of this tech-
nique can be found in research suggested by Fridrich [2], [3]. In the algorithm informa-
tion can be effectively embedded when the image is partitioned into blocks. However,
lossless compression technique should be employed to recover original image.
350
J. Hwang, J. Kim, and J. Choi
2.2 Reversible Watermarking Algorithms Based on Space Expansion
These algorithms generate a small value that contain characteristics of original image
and then expand the value to embed into the expanded space. Very frequently water-
mark is embedded into LSB of the expanded space. In the algorithm suggested by
Tian, characteristic values of original images are generated using difference values of
images and average values and then watermark information are embedded into the
space expanded by characteristic values using Integer Wavelet Transform [5]. This
technique is very effective in low frequency images in which differences between
pixels are small, because it utilizes difference values of images.
2.3 Reversible Watermarking Algorithms Based on Histograms
These algorithms generate information embedding space by modifying histogram
values and then embed watermark data. The algorithm suggested by Ni chooses maxi-
mum value and minimum value of histogram and then modifies histogram values,
showing excellent PSNR and highly increased amount of data embedding. However, a
significant disadvantage of the algorithm is that it requires additional information in
recovering original images [1]. Algorithm suggested by SK Lee embeds information
into locations where the values of the difference images are –1 or +1 and partially
solve the problem of Ni’s algorithm [11]. However, because of modulo operations
required to solve overflow phenomenon, it shows Salt & Pepper noisy problem [11].
Existing algorithms show differences and similarities between the algorithms and
continue to improve their performance through complimentary approaches. In this
research, a reversible watermarking algorithm is suggested based on histogram and it
shows excellent performance measured by imperceptibility while it can allow much
more information to be embedded into images.
3 A New Reversible Watermarking Algorithm
The algorithm suggested in this research embeds information by shifting pixels that
are located between maximum point and minimum point of histogram. As the charac-
teristics of images show that pixels located left point and right point of the maximum
point take big values, and therefore those pixels are also selected for embedding pay-
load. Then, two minimum points are identified so that one minimum point is located
at left side of the maximum point while the other minimum point is located at the
right side of the maximum point. The selection can drastically reduce degradation in
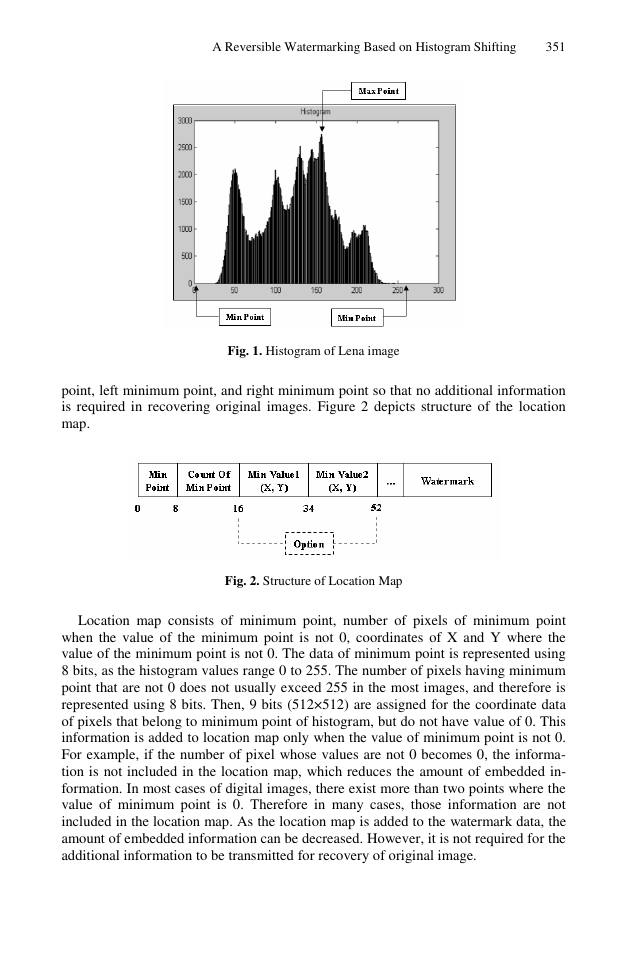
image transformation. Figure 1 shows how maximum point, left minimum point, and
right minimum point are selected in the histogram of Lena image (512×512×8). In
selecting locations of payload, the maximum point is 155, while the left minimum
point and right minimum point are 0 and 255, respectively.
3.1 Location Map
In the suggested algorithm, different from the algorithm suggested by Z. Ni [1], loca-
tion map is generated to store location information of the pixels that have maximum
A Reversible Watermarking Based on Histogram Shifting
351
Fig. 1. Histogram of Lena image
point, left minimum point, and right minimum point so that no additional information
is required in recovering original images. Figure 2 depicts structure of the location
map.
Fig. 2. Structure of Location Map
Location map consists of minimum point, number of pixels of minimum point
when the value of the minimum point is not 0, coordinates of X and Y where the
value of the minimum point is not 0. The data of minimum point is represented using
8 bits, as the histogram values range 0 to 255. The number of pixels having minimum
point that are not 0 does not usually exceed 255 in the most images, and therefore is
represented using 8 bits. Then, 9 bits (512×512) are assigned for the coordinate data
of pixels that belong to minimum point of histogram, but do not have value of 0. This
information is added to location map only when the value of minimum point is not 0.
For example, if the number of pixel whose values are not 0 becomes 0, the informa-
tion is not included in the location map, which reduces the amount of embedded in-
formation. In most cases of digital images, there exist more than two points where the
value of minimum point is 0. Therefore in many cases, those information are not
included in the location map. As the location map is added to the watermark data, the
amount of embedded information can be decreased. However, it is not required for the
additional information to be transmitted for recovery of original image.
352
J. Hwang, J. Kim, and J. Choi
3.2 Histogram Shifting
In this algorithm, histogram values are shifted in order to embed payload data which
consists of locations map and randomly generated watermark information. Figure 3
depicts a mechanism in which histogram data is shifted in case of Lena image.
Fig. 3. Histogram Shifting Mechanism
Locations where payload data is embedded are left point and right point of the
maximum point. In Figure 3, the maximum point exists at the location of 155, and
therefore the locations of payload embedding are location of 154 and 156. To gener-
ate the embedding space, the pixels that are located in histogram between left mini-
mum point and left side of the maximum point (pixel value of 154) are shifted one
pixel left. To the contrary, the pixels that are located between right minimum point
and right side of the maximum point(pixel value of 156) are shifted right one pixel. In
this scheme, because we do not change the maximum point of histogram, the original
image can be easily recovered if we know information where the minimum points are
located. This process can be described in the following equation (1):
I
),('
j
i
=
⎧
⎪
⎨
⎪
⎩
,(
iI
,1 ),(
iI
if
,1),(
iI
if
),
j
-j
+
j
if I(i,j)
=
Max
<
min(
)
),(
L
j
iI
<
<
),(
Max
iI
j
<
min(
Max
)
R
(1)
In the equation, I'(i,j) is an image in which payload is embedded, while I(i,j) is an
original image. Max is the maximum point of histogram, while min(L) and min(R)
represent left and right minimum point, respectively.
3.3 Embedding Algorithm
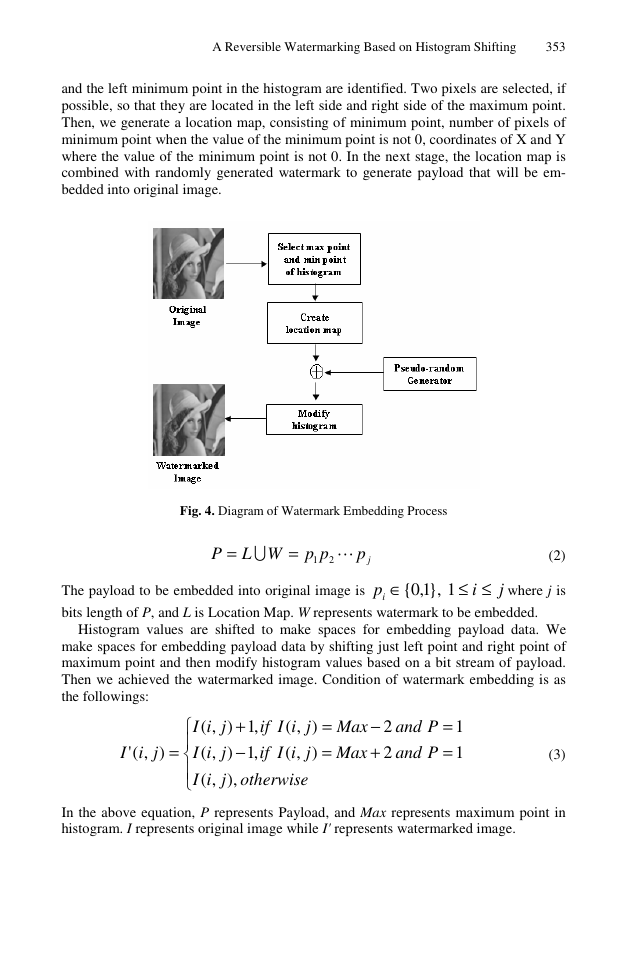
Figure 4 depicts embedding process of the suggested algorithm. At first, maximum
point of histogram of original image is identified and then pixels located at the right
A Reversible Watermarking Based on Histogram Shifting
353
and the left minimum point in the histogram are identified. Two pixels are selected, if
possible, so that they are located in the left side and right side of the maximum point.
Then, we generate a location map, consisting of minimum point, number of pixels of
minimum point when the value of the minimum point is not 0, coordinates of X and Y
where the value of the minimum point is not 0. In the next stage, the location map is
combined with randomly generated watermark to generate payload that will be em-
bedded into original image.
Fig. 4. Diagram of Watermark Embedding Process
ppWLP
∪
=
=
1
2
jp
(2)
1 },1,0{
≤≤
i
j
∈
pi
The payload to be embedded into original image is
bits length of P, and L is Location Map. W represents watermark to be embedded.
where j is
Histogram values are shifted to make spaces for embedding payload data. We
make spaces for embedding payload data by shifting just left point and right point of
maximum point and then modify histogram values based on a bit stream of payload.
Then we achieved the watermarked image. Condition of watermark embedding is as
the followings:
I
),('
j
i
=
⎧
⎪
⎨
⎪
⎩
,1),(
iI
,1),(
iI
,(
iI
+
),(
j
iI
−
),(
iI
j
),
otherwise
if
if
j
j
j
=
=
Max
Max
−
+
2
2
and
and
P
P
=
=
1
1
(3)
In the above equation, P represents Payload, and Max represents maximum point in
histogram. I represents original image while I' represents watermarked image.
354
J. Hwang, J. Kim, and J. Choi
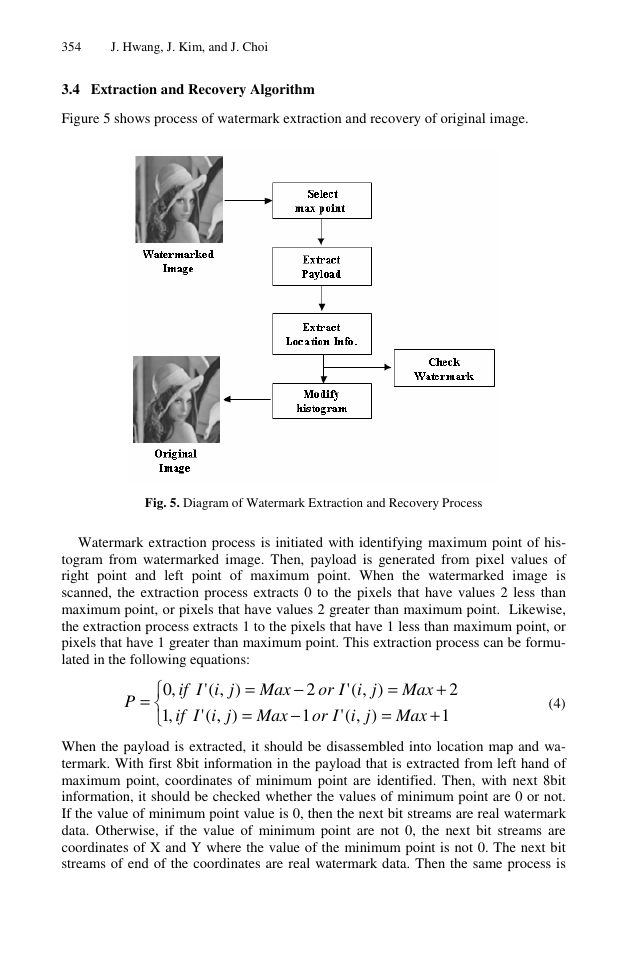
3.4 Extraction and Recovery Algorithm
Figure 5 shows process of watermark extraction and recovery of original image.
Fig. 5. Diagram of Watermark Extraction and Recovery Process
Watermark extraction process is initiated with identifying maximum point of his-
togram from watermarked image. Then, payload is generated from pixel values of
right point and left point of maximum point. When the watermarked image is
scanned, the extraction process extracts 0 to the pixels that have values 2 less than
maximum point, or pixels that have values 2 greater than maximum point. Likewise,
the extraction process extracts 1 to the pixels that have 1 less than maximum point, or
pixels that have 1 greater than maximum point. This extraction process can be formu-
lated in the following equations:
=
=
−
=
+
2
),('
2
Ior
j
Max
+
−
=
),('
1
1
Ior
Max
j
Max
Max
),('
I
j
),('
I
j
i
i
=
P
i
i
⎧
,0
if
⎨
,1
if
⎩
(4)
When the payload is extracted, it should be disassembled into location map and wa-
termark. With first 8bit information in the payload that is extracted from left hand of
maximum point, coordinates of minimum point are identified. Then, with next 8bit
information, it should be checked whether the values of minimum point are 0 or not.
If the value of minimum point value is 0, then the next bit streams are real watermark
data. Otherwise, if the value of minimum point are not 0, the next bit streams are
coordinates of X and Y where the value of the minimum point is not 0. The next bit
streams of end of the coordinates are real watermark data. Then the same process is
A Reversible Watermarking Based on Histogram Shifting
355
progressed in right side of maximum point. Finally, the watermarked image is authen-
ticated by calculating the correlation of extracted watermark and random watermark
generated using the private key.
Image recovery utilizes the location map information that is obtained from pay-
load. As the locations of minimum points are identified from location map, pixel
values can be calculated by assigning +1 or -1 to pixels that are located between
minimum points and maximum points. The process is described in the following
equation. In the equation Io represents recovered original image.
Io
),(
i
j
=
I
I
I
⎧
⎪
⎨
⎪
⎩
≤
)
L
<+
1
),('
i
I
j
),('
I
i
j
<
≤
−
1
Max
)
min(
R
(5)
,1),('
i
if
,1),('
i
if
,('
i
+
min(
−
Max
),
otherwise
j
j
j
Based on the equation, the first image recovery is done. When the minimum points
have value of zero, original image can be recovered completely. However, when the
minimum points have values of non-zeros, the pixels of minimum points should be
recovered using information additionally contained in location map. As the location
data of pixels that belong to minimum points but have non-zero values is included in
location map, it can be utilized in recovering minimum value pixels to original values
and then recovering back to original image without any information loss.
3.5 Algorithm Extension
The reversible watermarking algorithm suggested in this research has made it possible
to recover original image based on information of two points. In the same context, the
payload information can be extended repeatedly to contain information of minimum
points and maximum points in recovering original image. If the location map can be
extended to carry more information, 10 times more information than basic reversible
algorithm can be carried. The extended structure of location map is depicted in Figure 6.
Fig. 6. Structure of Extended Location Map
In the extended location map, 8 bits of data is added to show that there are more
than 2 points of information hiding. In the basic reversible watermark (BRW)
algorithm, no additional information is needed, because the maximum point of the
histogram does not change, and because the left side and right side of the maximum
point are easily identified even after watermark embedding. However, in order to
embed information into more than two points, the watermarking system needs infor-
mation of the largest value point, in addition to the left side pixel and right side pixel
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
