logo资料库

《应用回归分析》课后习题部分答案-何晓群版.doc

发布时间：2022-06-23 发布人：admin 分类：说明书 资料大小：1.32M 资料格式：doc 举报 版权申诉
第1页 / 共32页
第2页 / 共32页
第3页 / 共32页
第4页 / 共32页
第5页 / 共32页
第6页 / 共32页
第7页 / 共32页
第8页 / 共32页
资料共32页，剩余部分请下载后查看
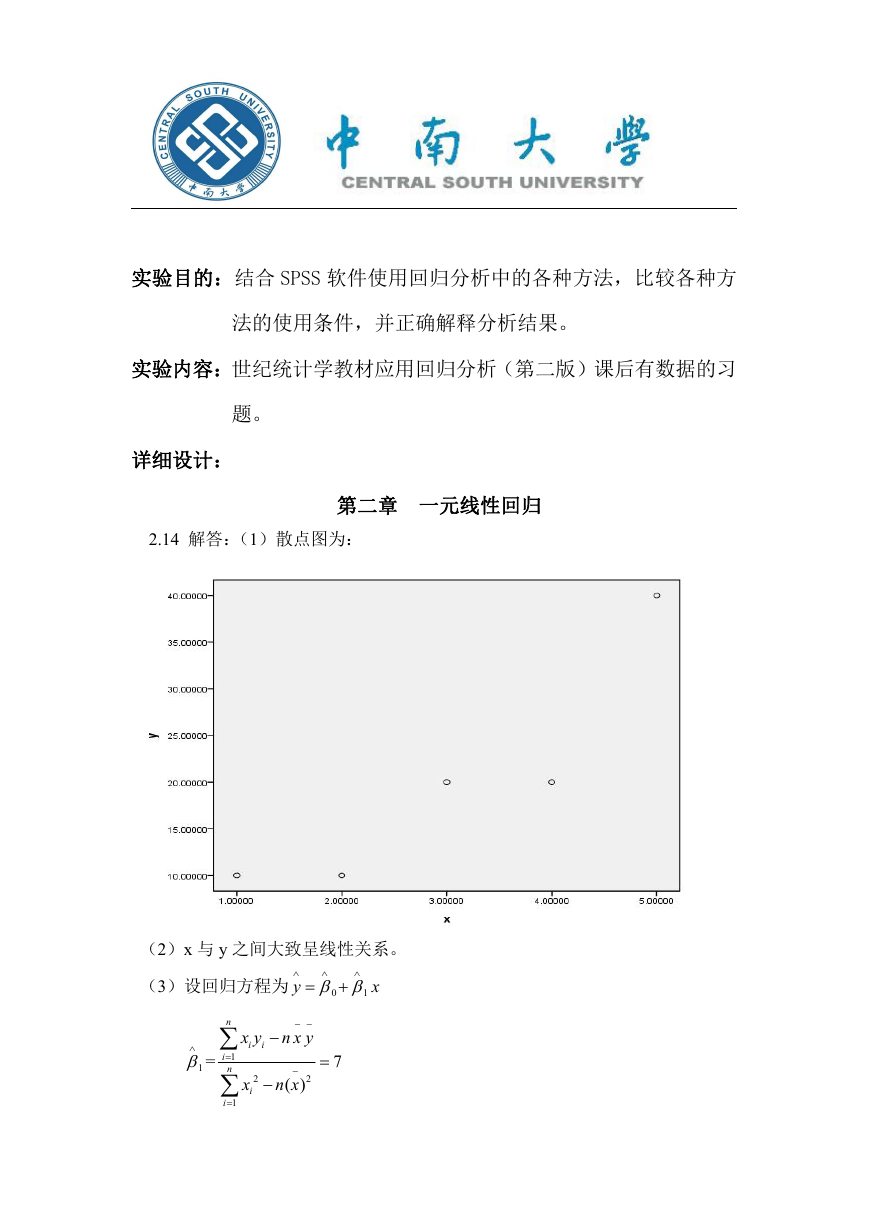
    实验目的：结合 SPSS 软件使用回归分析中的各种方法，比较各种方 法的使用条件，并正确解释分析结果。 实验内容：世纪统计学教材应用回归分析（第二版）课后有数据的习 题。 详细设计： 第二章 一元线性回归 2.14 解答：（1）散点图为： （2）x 与 y 之间大致呈线性关系。 （3）设回归方程为  y      1  0 x  1 n  = 1 i  n  i 1  x y i i    n x y 2 x i   ( ) n x 2  7
     y     x  1  0  20 7 3     1  可得回归方程为  y    1 7 x 2    （4）  1 n-2 1 n-2 n  y i ( i=1 2  y i ) ( iy    (   1  0 2 x )) n  i=1 2 2  =       2 2    1 （10-（-1+7 1）） （10-（-1+7 2）） （20-（-1+7 3））   3 2   （20-（-1+7 4）） （40-（-1+7 5））   1 16 9 0 49 36  3 110 / 3  1 330  3    6.1      （5）由于   1  N 1(  , 2  L xx ) t      1 1 2 / L  xx    ( )   1   L xx 服从自由度为 n-2 的 t 分布。因而 P   ( )   1     |   xxL |  ( t n /2  2) 1         (  也即： 1 p  t  /2   L xx    1 1    t  /2   L xx ) =1    可得 1 的置信度为 的置信区间为（7-2.353 95% 即为：（2.49，11.5）  ( ) x L   0 (  0 1 n ,( N   xx 2 2 )  )  1 3 33 ，7+2.353  1 3 33 ） 1
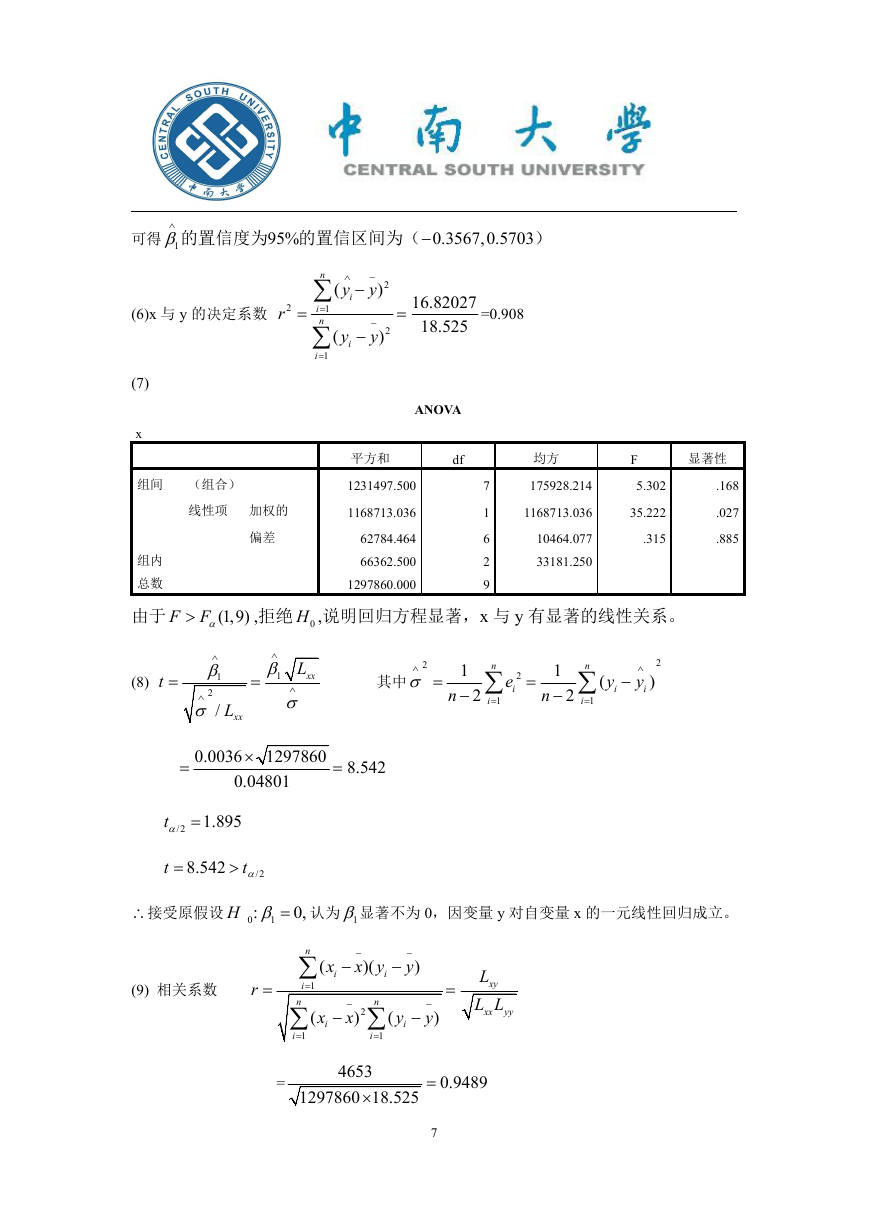
    t    0 0    ( ) x L xx ( 1 n   2 2     )     0  ( ) x L 0 1 n  xx 2 服从自由度为 n-2 的 t 分布。因而            0  ( ) x L    |      0 1 n   t  2) P    ( n  /2 xx | 2 1    即 p   (    0 1 n   ( ) x L xx 2 t /2          0 0 1 n   ( ) x L xx 2 t /2  ) 1      可得 1 的置信度为 的置信区间为（ 95%  7.77,5.77 ） （6）x 与 y 的决定系数 2 r  （7） x 组间 （组合） 线性项 加权的 偏差 组内 总数  y i (   y ) 2 ( y i   y ) 2  490 / 600 0.817  n   1 i  n i 1  ANOVA 平方和 df 均方 9.000 8.167 .833 1.000 10.000 4.500 8.167 .833 .500 2 1 1 2 4 F 9.000 16.333 1.667 显著性 .100 .056 .326 由于 F F (1,3) ,拒绝 0H ,说明回归方程显著，x 与 y 有显著的线性关系。 （8） t    1 2   / L xx   1  L xx   2    其中 1  2 n 2 n  i 1  2 e i  1  2 n 2  y i ) ( y i  n  i 1 
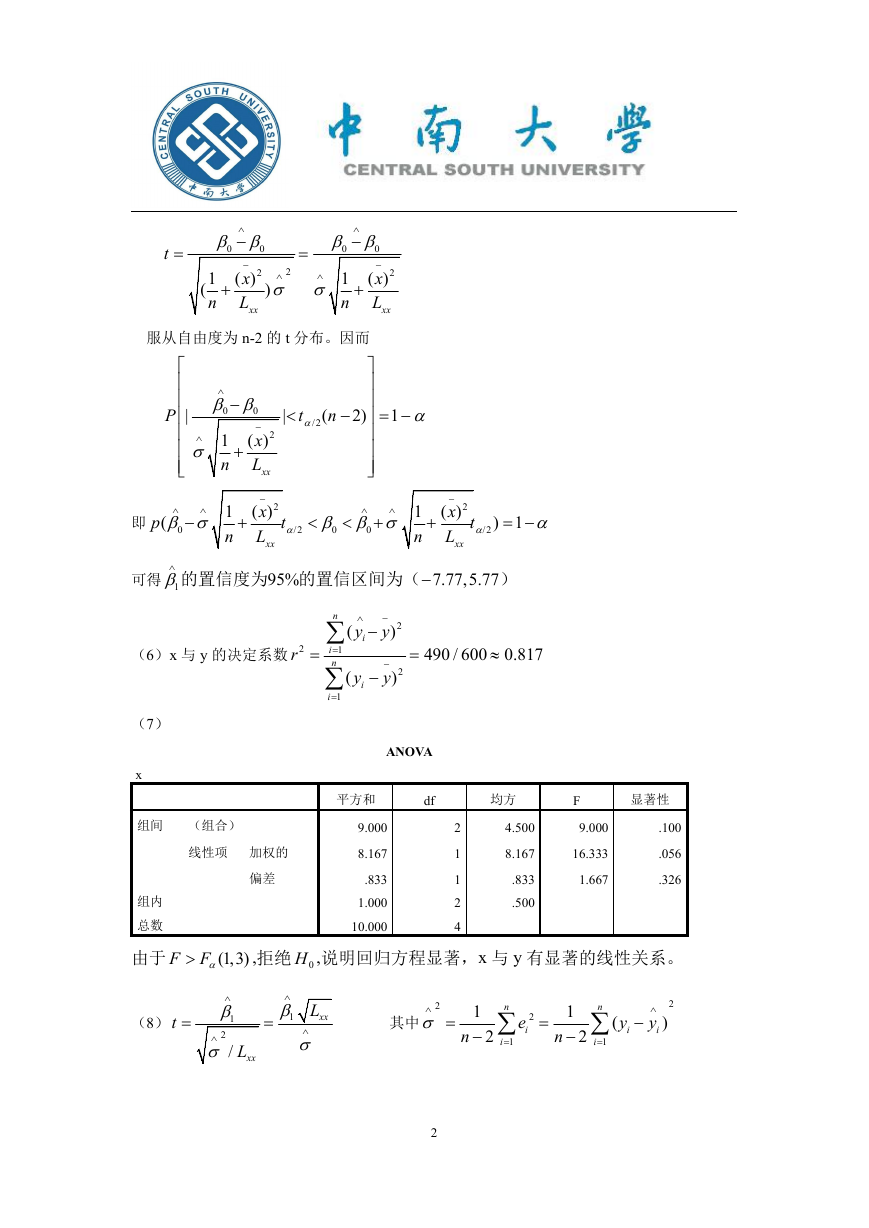
     10 330  7 1 3  21 33  3.66 t  /2 2.353 t  3.66  t /2 接受原假设 0 H   认为 1显著不为 0，因变量 y 对自变量 x 的一元线性回归成立。 0, : 1 （9）相关系数 r  ( x i   )( x y i  y )  n  i 1  ( x i   x ) 2 n  i 1  n  i 1  ( y i   y )  L xy L L xx yy =  70  7 60 r 小于表中 1% 的相应值同时大于表中 (10) 序号 10 600 y x 1 2 3 4 5 残差图为： 1 2 3 4 5 10 10 20 20 40  0.904 5% 的相应值，x 与 y 有显著的线性关系.  y 6 13 20 27 34 e 4 -3 0 -7 6 3
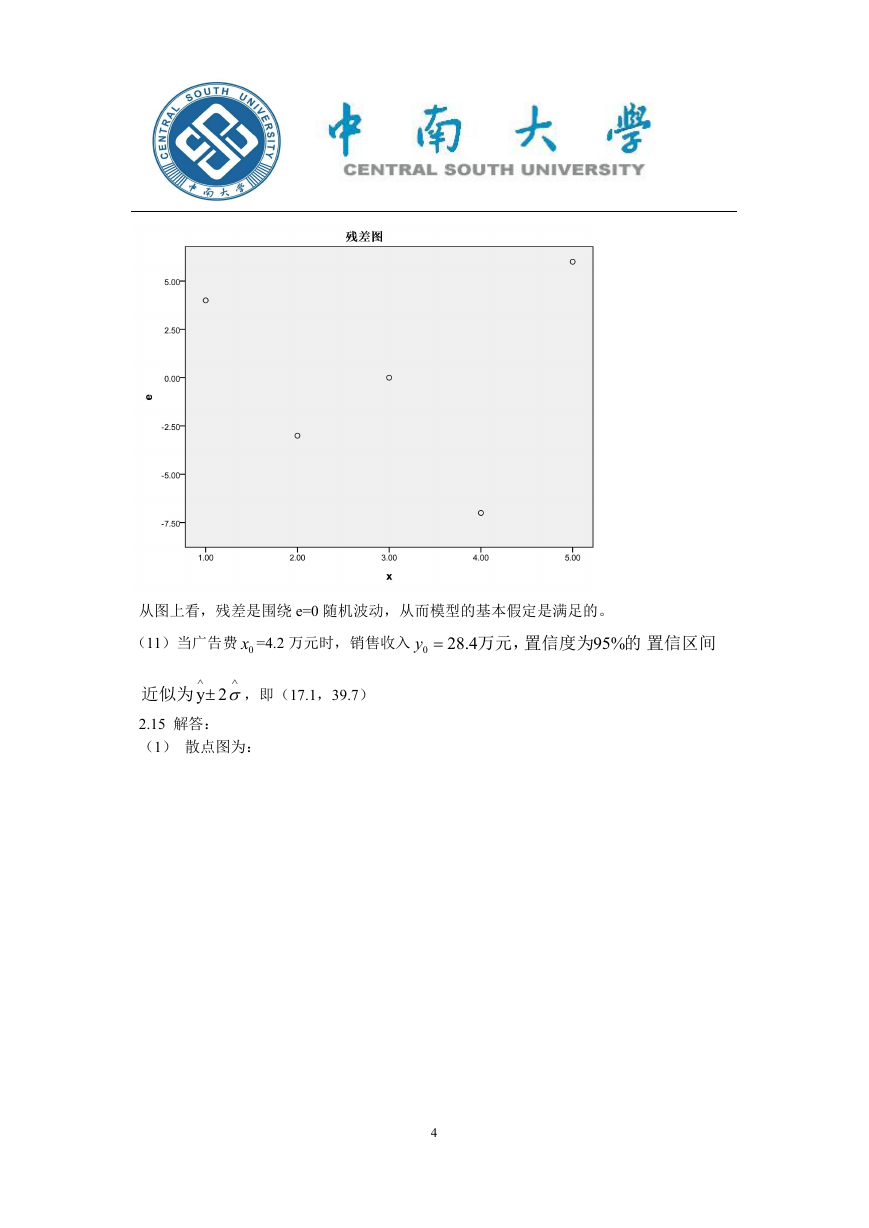
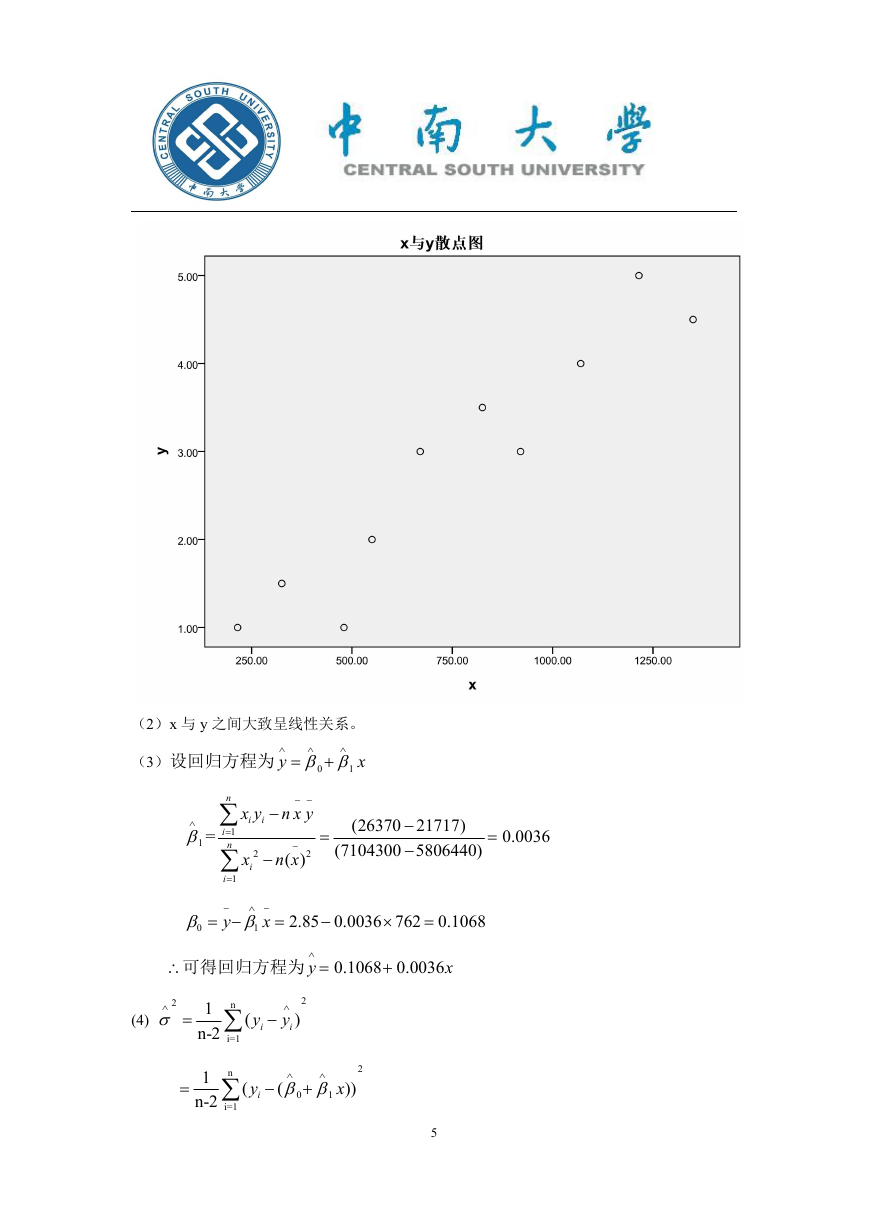
    从图上看，残差是围绕 e=0 随机波动，从而模型的基本假定是满足的。 （11）当广告费 0x =4.2 万元时，销售收入 0 y  万元， 28.4 置信度为 的 置信区间 95% ，即（17.1，39.7） 近似为   y 2  2.15 解答： （1） 散点图为： 4
    （2）x 与 y 之间大致呈线性关系。 （3）设回归方程为  y      1  0 x  1 n  = 1 i  n  i 1  x y i i    n x y 2 x i   ( ) n x 2  (26370 21717) (7104300 5806440)    0.0036  y     x  1   0 2.85 0.0036 762 0.1068     可得回归方程为  y  0.1068 0.0036  x 2    (4) 1 n-2  1 n-2 n  y i ( i=1 2  y i ) n  i=1 ( iy    (   1  0 2 x )) 5
    =0.2305    0.4801 (5) 由于   1  N 1(  , 2  L xx ) t      1 1 2 / L  xx    ( )   1   L xx 服从自由度为 n-2 的 t 分布。因而 P   ( )   1     |   xxL |  ( t n /2  2) 1         (  也即： 1 p  t  /2   L xx    1 1    t  /2   L xx ) =1    可得 1 的置信度为 的置信区间为 95% （0.0036-1.860  0.4801/ 1297860 ，0.0036+1.860  0.4801/ 1297860 ） 即为：（0.0028，0.0044）   0  N (  0 ,( 1 n  2 2 )  )  ( ) x L xx t    0 0    ( ) x L xx ( 1 n   2 2     )     0  ( ) x L 0 1 n  xx 2 服从自由度为 n-2 的 t 分布。因而            0  ( ) x L    |      0 1 n   t  2) P   ( n   /2 xx | 2 1    即 p   (    0 1 n   ( ) x L xx 2 t /2          0 0  ( ) x L xx 2 t /2  ) 1    1 n  6
      可得 1 的置信度为 的置信区间为（ 95%  0.3567,0.5703 ） (6)x 与 y 的决定系数 2 r  (7) x n i   1  n i 1   y i (   y ) 2 ( y i   y ) 2  16.82027 18.525 =0.908 ANOVA 组间 （组合） 线性项 加权的 偏差 组内 总数 平方和 1231497.500 1168713.036 62784.464 66362.500 1297860.000 df 均方 175928.214 1168713.036 10464.077 33181.250 7 1 6 2 9 F 5.302 35.222 .315 显著性 .168 .027 .885 由于 F F (1,9) ,拒绝 0H ,说明回归方程显著，x 与 y 有显著的线性关系。 (8) t    1 2   / L xx   1  L xx   2    其中 1  2 n n  i 1  2 e i  1  2 n n  i 1  2  y i ) ( y i   0.0036 1297860  0.04801  8.542 t  /2 1.895 t  8.542  t /2 接受原假设 0 H   认为 1显著不为 0，因变量 y 对自变量 x 的一元线性回归成立。 0, : 1 (9) 相关系数 r  ( x i   )( x y i  y )  n  i 1  ( x i   x ) 2 n  i 1  n  i 1  ( y i   y )  L xy L L xx yy = 4653  1297860 18.525  0.9489 7
    分享到：
    赞 收藏

    相关推荐

    资料库

    操作系统

    共收录1433份资料，累计11个分类，关注成员有19位，主要包括：CentOS,MacOS,DOS,Solaris,Ubuntu,Unix,OS,桌面系统,其它,Windows Server,Linux

    热门标签

    CentOS MacOS DOS Solaris Ubuntu Unix OS 桌面系统 其它 Windows Server Linux

    最新资料