2023年浙江温州中考数学真题及答案.doc-资料库

第1页 / 共13页

第2页 / 共13页

第3页 / 共13页

第4页 / 共13页

第5页 / 共13页

第6页 / 共13页

第7页 / 共13页

第8页 / 共13页

2023 年浙江温州中考数学真题及答案卷Ⅰ 一、选择题（本题有 10 小题，第 1-5 小题，每小题 3 分，第 6-10 小题，每小题 4 分，共 35 分，每小题只有一个选项是正确的，不选、多选、错选，均不给分） 1.如图，比数轴上点 A表示的数大 3 的数是（） A.-1 B.0 C.1 D.2 2.截面为扇环的几何体与长方体组成的摆件如图所示，它的主视图是（） A B C D 3.苏步青来自“数学家之乡”，为纪念其卓越贡献，国际上将一颗距地球约 218000000 公里的行星命名为“苏步青星”.数据 218000000 用科学记数法表示为（） A. 9 0.218 10 B. 8 2.18 10 C. 21.8 10 7 D. 218 10 6 阅读背景素材，完成第 4—5 题. 某校计划组织研学活动，现有四个地点可供选择：南麂岛、百丈漈、楠溪江、雁荡山. 4.若从中随机选择一个地点，则选中“南麂岛”或“百丈漈”的概率为（） A. 1 4 B. 1 3 C. 1 2 D. 2 3 5.为了解学生想法，校方进行问卷调查（每人选一个地点），并绘制成如图所示统计图.已知选择雁荡山的有 270 人，那么选择楠溪江的有（） A.90 人 6.化简 4 a B.180 人 C.270 人 D.360 人 (   的结果是（ a 3 ) ）

A. 12a B. 12a C. 7a D. 7a 7.一瓶牛奶的营养成分中，碳水化合物含量是蛋白质的 1.5 倍，碳水化合物、蛋白质与脂肪的含量共 30g.设蛋白质、脂肪的含量分别为  y g ，可列出方程为（ x g ，  ）   A. 5 2 x y  30 B. x y 5 2  30 C. 3 2 x y  30 D. x y 3 2  30 8.图 1 是第七届国际数学教育大会（ICME）的会徽，图 2 由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF ，使点 D，E，F分别在边 OC ，OB ，BC 上，过点 E作 EH AB 于点 H.当 AB BC  ， DE  时， EH 的长为（ BOC ， 30 ） 2  A. 3 B. 3 2 C. 2 D. 4 3 9.如图，四边形 ABCD 内接于 O ， BC 度数与 BC 的长分别为（） AD∥ ， AC BD .若 AOD  120  ， AD  ，则 CAO 3 的 A.10°，1 B.10°， 2 C.15°，1 D.15°， 2 10.【素材 1】某景区游览路线及方向如图 1 所示，①④⑥各路段路程相等，⑤⑦⑧各路段路程相等，②③两路段路程相等. 【素材 2】设游玩行走速度恒定，经过每个景点都停留 20 分钟.小温游路线①④⑤⑥⑦⑧用时 3 小时 25 分钟；小州游路线①②⑧，他离入口的路程 s与时间 t的关系（部分数据）如图 2 所示，在 2100 米处，他到出口还要走 10 分钟. 【问题】路线①③⑥⑦⑧各路段路程之和为（）

A.4200 米 B.4800 米 C.5200 米 D.5400 米卷Ⅱ 二、填空题（本题有 6 小题，第 11—15 小题，每小题 4 分，第 16 小题 5 分，共 25 分） 11.分解因式： 22 a 2 a  ____________. 12.某校学生“亚运知识”竞赛成绩的频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，其中成绩在 80 分及以上的学生有___________人. 13.不等式组 3 2 x   3 1 4 x     2 的解是___________. 14.若扇形的圆心角为 40°，半径为 18，则它的弧长为___________. 15.在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，加压后气体对汽缸壁所产生的压强 p （ kPa ）与汽缸内气体的体积 V（ mL ）成反比例，p关于 V的函数图象如图所示.若压强由 75 kPa 加压到 100 kPa ，则气体体积压缩了___________ mL . 16.图 1 是 4 4 方格绘成的七巧板图案，每个小方格的边长为 2 ，现将它剪拼成一个“房子”造型（如图 2），过左侧的三个端点作圆，并在圆内右侧部分留出矩形 CDEF 作为题字区域（点 A，E，D，B在圆上，点 C，F 在 AB 上），形成一幅装饰画，则圆的半径为___________.若点 A，N，M在同一直线上，AB PN∥ ， DE  6 EF ，

则题字区域的面积为___________. 三、解答题（本题有 8 小题，共 90 分.解答需写出必要的文字说明、演算步骤或证明过程） 1     8 3 2     1 3     4    . 17.（本题 10 分）计算：（1）（2） 2 a a 2  1   3  1 a . 18.（本题 10 分）如图，在 2 4 的方格纸 ABCD 中，每个小方格的边长为 1.已知格点 P，请按要求画格点三角形（顶点均在格点上）. （1）在图 1 中画一个等腰三角形 PEF ，使底边长为 2 ，点 E在 BC 上，点 F在 AD 上，再画出该三角形绕矩形 ABCD 的中心旋转 180°后的图形. （2）在图 2 中画一个 Rt PQR△ ，使 P  45  ，点 Q在 BC 上，点 R在 AD 上，再画出该三角形向右平移 1 个单位后的图形. 注：图 1，图 2 在答题纸上. 19.（本题 10 分）某公司有 A，B，C三种型号电动汽车出租，每辆车每天费用分别为 300 元、380 元、500 元. 阳阳打算从该公司租一辆汽车外出旅游一天，往返行程为 210 km ，为了选择合适的型号，通过网络调查，获得三种型号汽车充满电后的里程数据如图所示. 平均里程（ km ）中位数（ km ）众数（ km ）型号 B C 216 225 215 227.5 220 227.5

（1）阳阳已经对 B，C型号汽车数据统计如下表，请继续求出 A型号汽车的平均里程、中位数和众数. （2）为了尽可能避免行程中充电耽误时间，又能经济实惠地用车，请你从相关统计量和符合行程要求的百分比等进行分析，给出合理的用车型号建议. 20.（本题 10 分）如图，在直角坐标系中，点  2,A m 在直线  y 2 x  上，过点 A的直线交 y轴于点  B 5 2 0,3 . （1）求 m的值和直线 AB 的函数表达式. （2）若点  ,P t y 在线段 AB 上，点  Q t 1 21, y 在直线 y 2 x  上，求 1 y 5 2 y 的最大值. 2 21.（本题 11 分）如图，已知矩形 ABCD ，点 E在 CB 延长线上，点 F在 BC 延长线上，过点下作 FH EF 交 ED 的延长线于点 H，连结 AF 交 EH 于点 G， GE GH . （1）求证： BE CF . （2）当 AB FH  ， 5 6 AD  时，求 EF 的长. 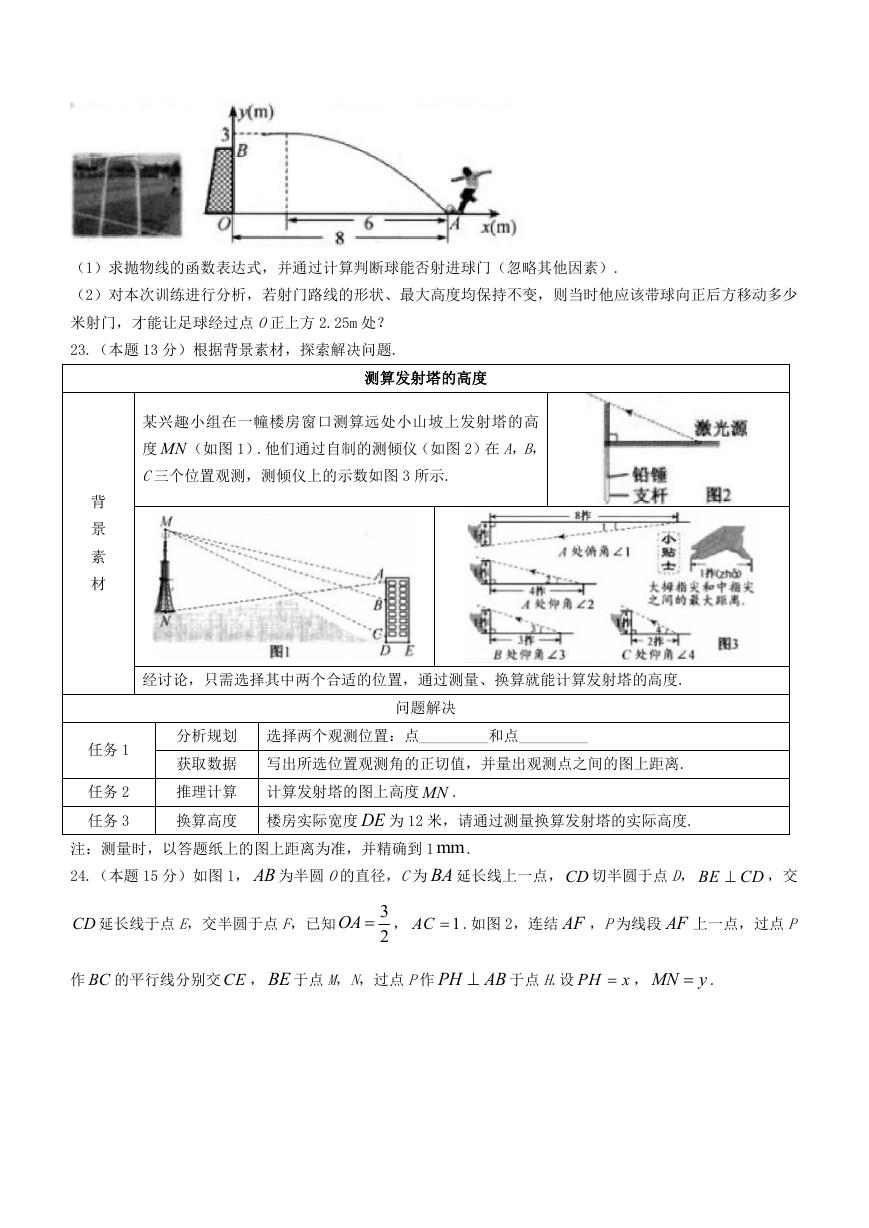4 22.（本题 11 分）一次足球训练中，小明从球门正前方 8m 的 A处射门，球射向球门的路线呈抛物线.当球飞行的水平距离为 6m 时，球达到最高点，此时球离地面 3m.已知球门高OB 为 2.44m，现以 O为原点建立如图所示直角坐标系.

（1）求抛物线的函数表达式，并通过计算判断球能否射进球门（忽略其他因素）. （2）对本次训练进行分析，若射门路线的形状、最大高度均保持不变，则当时他应该带球向正后方移动多少米射门，才能让足球经过点 O正上方 2.25m 处？ 23.（本题 13 分）根据背景素材，探索解决问题. 测算发射塔的高度某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度 MN （如图 1）.他们通过自制的测倾仪（如图 2）在 A，B， C三个位置观测，测倾仪上的示数如图 3 所示. 背景素材经讨论，只需选择其中两个合适的位置，通过测量、换算就能计算发射塔的高度. 问题解决任务 1 任务 2 任务 3 分析规划选择两个观测位置：点_________和点_________ 获取数据写出所选位置观测角的正切值，并量出观测点之间的图上距离. 推理计算计算发射塔的图上高度 MN . 换算高度楼房实际宽度 DE 为 12 米，请通过测量换算发射塔的实际高度. 注：测量时，以答题纸上的图上距离为准，并精确到 1 mm . 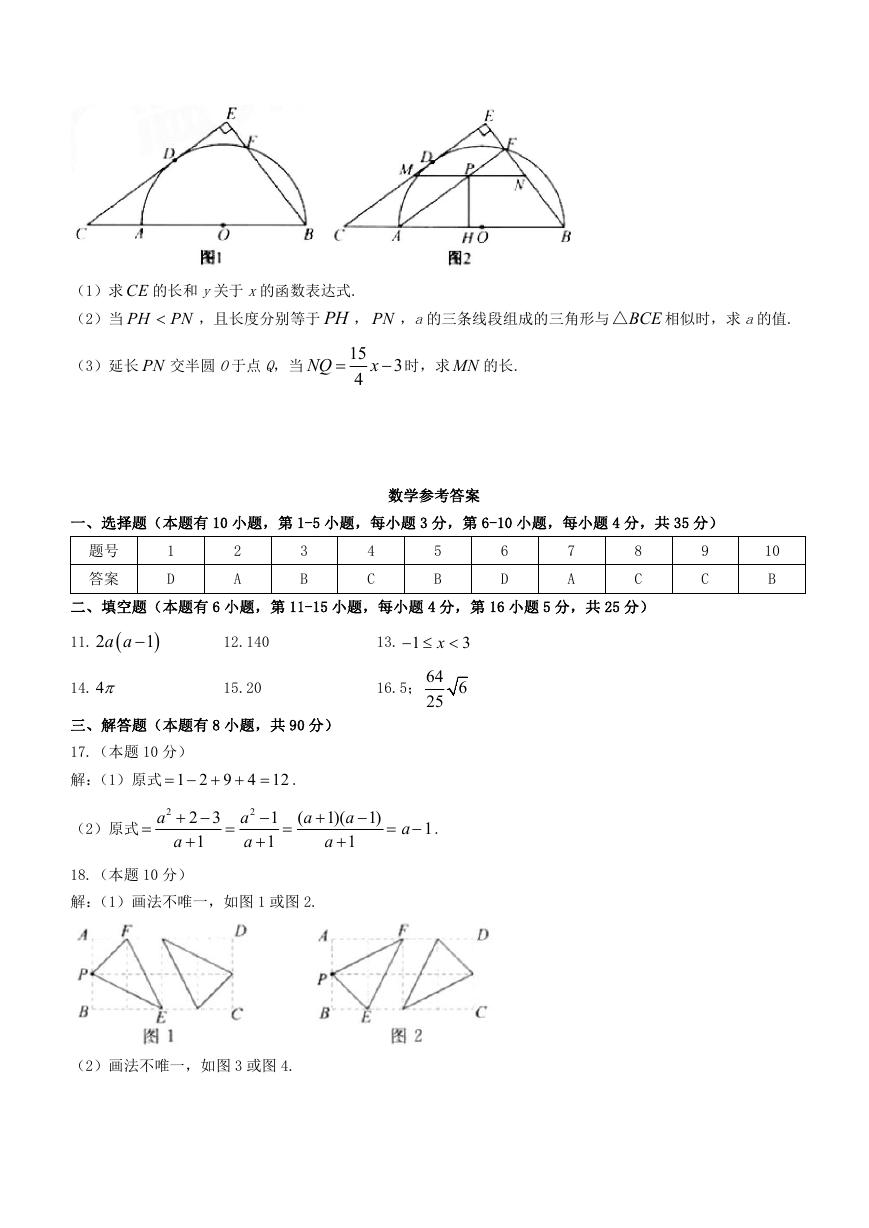24.（本题 15 分）如图 1， AB 为半圆 O的直径，C为 BA 延长线上一点，CD 切半圆于点 D， BE CD ，交 CD 延长线于点 E，交半圆于点 F，已知 OA  ， 3 2 AC  .如图 2，连结 AF ，P为线段 AF 上一点，过点 P 1 作 BC 的平行线分别交CE ， BE 于点 M，N，过点 P作 PH AB 于点 H.设 PH x ， MN y .

（1）求 CE 的长和 y关于 x的函数表达式. （2）当 PH PN ，且长度分别等于 PH ， PN ，a的三条线段组成的三角形与 BCE△ 相似时，求 a的值. （3）延长 PN 交半圆 O于点 Q，当 NQ  15 4 x 3  时，求 MN 的长. 数学参考答案一、选择题（本题有 10 小题，第 1-5 小题，每小题 3 分，第 6-10 小题，每小题 4 分，共 35 分）题号答案 1 D 2 A 3 B 4 C 5 B 6 D 7 A 8 C 9 C 10 B 二、填空题（本题有 6 小题，第 11-15 小题，每小题 4 分，第 16 小题 5 分，共 25 分） 11. 2  a a   1 14. 4 12.140 15.20 三、解答题（本题有 8 小题，共 90 分） 17.（本题 10 分）解：（1）原式 1 2 9 4 12      . 13. 1 3 x    64 6 25 16.5；（2）原式 2 a  2 3   1 a   2 a a 1  1   ( a 1)( a  1 a   1) a   1 . 18.（本题 10 分）解：（1）画法不唯一，如图 1 或图 2. （2）画法不唯一，如图 3 或图 4.

19.（本题 10 分）解：（1）方法一： Ax  方法二： Ax  200   200(km) .  200 0   200(km) 3 190 4 195 5 200 6 205 2 210          3 4 5 6 2     3 ( 10) 4 ( 5) 5 0 6 5 2 10            3 4 5 6 2     中位数： 200km ，众数： 205km . （2）评分参考：【A 等级】合理选择，完整说理. 选择 B 型号汽车.理由： A 型号汽车的平均里程、中位数、众数均低于 210km ，且只有 10%的车辆能达到行程要求，故不建议选择； B ，C 型号汽车的平均里程、中位数、众数都超过 210km ，其中 B 型号汽车有 90%符合行程要求，很大程度上可以避免行程中充电耽误时间，且 B 型号汽车比C 型号汽车更经济实惠，故建议选择 B 型号汽车. 【B 等级】合理选择但理由不全面. 选择 B 型号汽车，理由不全面. 【C 等级】合理选择但说理不恰当或选择不恰当但说理片面. 选择 B 型号汽车，理由不全面且存在不恰当分析. 选择 A 型号汽车，从经济实惠角度进行说理. 选择 C 型号汽车，只从统计量说明行驶里程符合要求. 【D 等级】合理选择未作说理或同时多型号选择等. 选择 B 型号汽车，未作说理. 同时选择两种或三种型号汽车，并给出一定理由. 【E 等级】未作答等. 20.（本题 10 分）解：（1）把点  2,A m 代入  y 2 x  ，得 5 2 3 m  . 2 设直线 AB 的函数表达式为 y  kx b  ，把点 A   32, 2    ，  B 0,3 代入得 k b    2     b 3. 3 2 ，解得 3 4    k     3. b ， ∴直线 AB 的函数表达式为 3 4 ,P t y 在线段 AB 上，   y 1 （2）∵点  x 3  .

资料库

2023年浙江温州中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料