http://www.paper.edu.cn 扩散方程中源项线性化问题的研究 张敏，胡文斌，李磊，许彬，卢学山 南京理工大学动力工程学院，南京 (210094) 摘 要：用微分方法对扩散方程源项进行线性化处理。以此保证数值计算的收敛性和精确性。 在二个热传导算例的基础上，证明和展示本方法的可行性和实用性。 关键词：方程源项，线性化，扩散方程 扩散方程是自然界中描述物理过程三大类型方程之一，它最常用的形式是对导热扩散过 程的描述。对于扩散方程中源项的数值离散，在数值模拟计算中是十分重要的。在这方面美 国学者 Patankar[1-2]和新加坡学者 Chai[3-4]做了许多工作。 本文对扩散基本方程源项的线性化进行系统的描述，并通过两个算例，给出在非结构 化网格中，对源项的具体操作过程。 1 方程源项线性化的基本概念和关系式 非稳态的扩散方程或导热方程，对一个标量物理变量φ 可写成， c ρ p ∂ φ t ∂ = ∂ x ∂ i ⎛ ⎞ ∂ φ Γ ⎜ ⎟ x ∂⎝ ⎠ i + S φ (1.1) 其中， φS 是单位体积中的净源项，Γ是对应于变量φ 的扩散系数。对于方程（1.1）中的源 项，可以分成两个部分， S φ = S c + S φ p p (1.2) 其中， cS 和 pS 为常数项。在有限容积方法中，对于一个控制容积 P，式（1.2）为对标量 pφ 的线性方程。 当源项 φS 为一个非线性函数时， cS 和 pS 两量也将变成标量 pφ 的函数值，此时在数值 计算中，我们不得不通过叠代来更新它们的值。在进行 cS 和 pS 线性化中，有许多方法可以 选择，这其中有一种最佳的方法形式如下式所示， S φ = * S + ( dS d φ ) ( * * φ φ p − p ) (1.3) 在这里，假设 φS 为φ的一阶可微函数。星号*表示当前时刻的估计值，如初始值或猜测值。 比较方程（1.2）和（1.3），可得到， S c = * S − S p = ( ( dS ) * * φ p d φ dS ) * dφ (1.4a) (1.4b) 对于 pS 在此有严格的要求，它必须小于零；否则 pS 设为零，即整个源项为 cS 。下面通过 例子来解释这方面的处理技巧。 7, 1、当 7 3 = = − ，显然有 3 = − φ S S S C P - 1 - 

http://www.paper.edu.cn 2、当 6 5 = + ，如果我们选取 φ S 的。因此另一种选择为， S C S = + S= 6, C Sφ 6 5 , * P P = ，将得到 PS 为正值，这是我们不希望出现 5 P = ，这其中， CS 必须不断叠代更新。 0 3、当 S = − ，我们采用公式(1.4)有， 2 3 3 φ S c = * S − ( dS ) * * φ p d φ 2 3 = − *3 *3 φ φ P P + 9 S p = ( dS ) * d φ = − 9 *2 φ P = + 2 6 *3 φ P (1.5a) (1.5b) 3 φ S 2 3 = + 2 3 = + Sφ , *3 P ， 如 果 我 们 还 采 用 公 式 (1.4) 将 会 导 致 PS 为 正 值 ， 所 以 有 0 这样我们确保了 PS 为负值。当然我们还有另外的选择。 4 、 当 S 对于方程源项为自变量函数时，它的线性化对收敛求解离散方程十分重要。所谓的线性 化就是采用公式(1.4)保证 PS 不为正值。当然，在保证 PS 不为正值时，源项的处理是有多种 可能的。下面结合实际，给出两个算例。 = 。 C P 2 算例分析 算例 1. 二维稳态扩散问题：假设有温度扩散方程（极坐标）， 1 r ∂ r ∂ ⎛ ⎜ ⎝ kr T ∂ r ∂ ⎞ + ⎟ ⎠ sin(2 ) 0 ϕ = (2.1a) 因为, 方程源项为与自变量 T 无关的函数，我们可取， (2.1b) 图 1 为温度场计算结果。同时，图 2-4 给出了按下列源项计算的结果。如果读者愿意从审美 的视角出发，我们不难找到科学的艺术性 [5-6] p c S = sin(2 ) ϕ , S 0 = sin(3 ), ϕ cos(2 ), ϕ 。 cos(3 ). ϕ (2.1c) - 2 - 

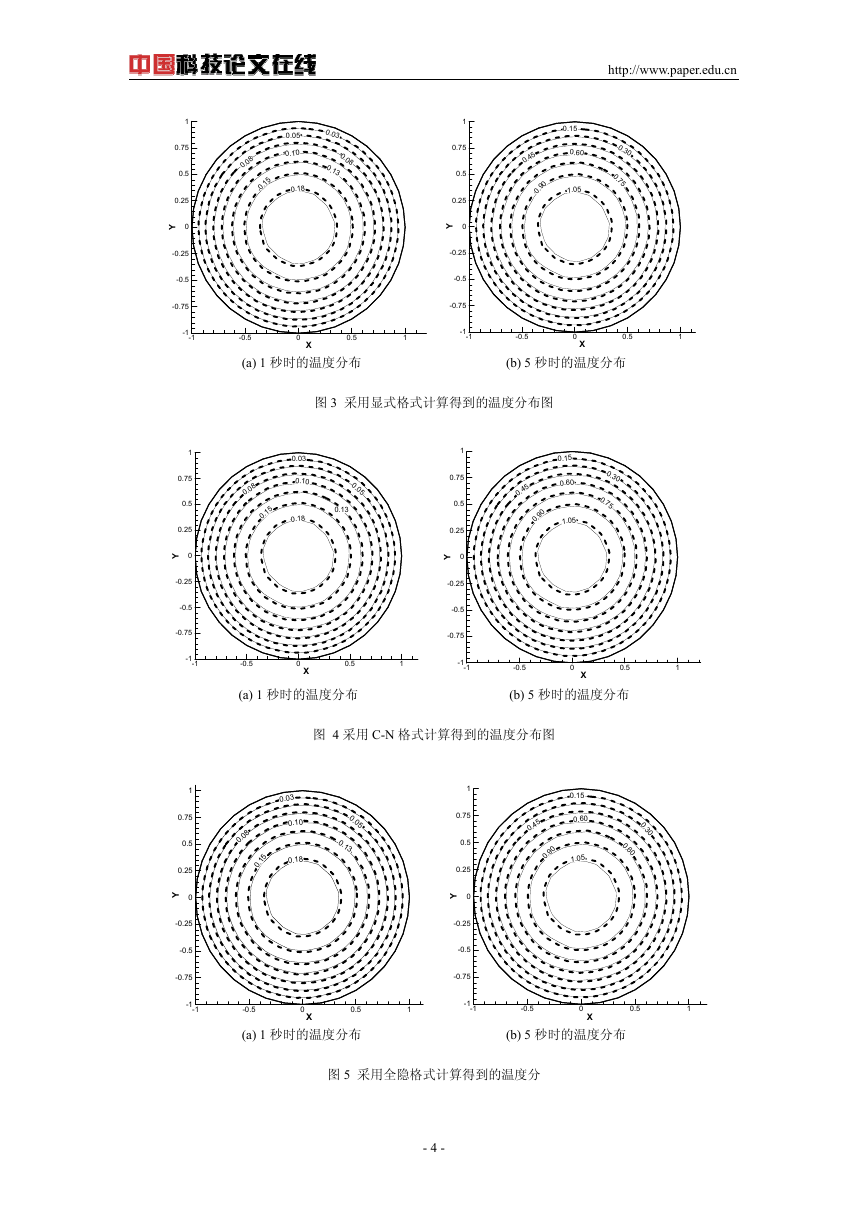
http://www.paper.edu.cn 图 1 不同源项温度场分布 算例 2. 二维非稳态扩散问题：实心圆柱体，初始温度为零度，在 物体内产生热量，单位体积发热率为 态导热方程和精确解[7-8]为， 的时间段内， ；在 Rr = 的边界处，温度保持为零度。非稳 tq =)( ≤< t 5 s 0 t (2.2a) (2.2b) (2.2c) c ρ p 2 αβ − m e trT ),( ∞ ∑= 2 α R λ 1m = T ∂ t ∂ J J t = 1 ∂ r r ∂ r ) ( β m 0 R ) ( β m 1 kr T ∂ r ∂ ⎞ ⎟ ⎠ + t q e )( τ 2 αβ − m t d τ （ 0 ≤< t 5 s ） ⎛ ⎜ ⎝ t ∫ 0 源项的处理有， S c t ∗= p , S p 0 = 图 2 圆域的网格划分 s .0=∆τ 0005 采用显式格式，时间步长 ，计算结果如图 3 所示。时间步长再增大就有 5= 时的温度分布，时间步长 可能发散。采用 C-N 格式和全隐格式计算了 .0=∆τ ，计算结果如图 4 和图 5 所示。表 1 给出了三种格式计算的平均误差。由图 中的温度分布可以看出，数值解与精确解基本重合，在趋近圆心的计算结果吻合得不好，对 于该处计算误差比较大。 t 1= 和 0005 s s s t 时间 τ(s) 1 5 表 1 三种格式计算的平均误差 显式格式 3.43% 4.67% C-N 格式 2.89% 3.67% 全隐格式 2.34% 3.12% - 3 - 

http://www.paper.edu.cn 0.15 0.60 0.4 5 0.90 1. 05 0.30 0.7 5 0.08 0.05 0 .1 0 0.15 0. 18 0.03 0.08 0.13 1 0.75 0.5 0.25 Y 0 -0.25 -0.5 -0.75 1 0.75 0.5 0.25 Y 0 -0.25 -0.5 -0.75 -1 -1 -0.5 0 X 0.5 1 -1 -1 -0.5 0 X 0.5 1 (a) 1 秒时的温度分布 (b) 5 秒时的温度分布 图 3 采用显式格式计算得到的温度分布图 0.0 8 0.03 0.10 0.15 0 .18 0.0 5 0.13 1 0.75 0.5 0.25 Y 0 -0.25 -0.5 -0.75 1 0.75 0.5 0.25 Y 0 -0.25 -0.5 -0.75 0.4 5 0.15 0 .6 0 0.90 1. 05 0.30 0.75 -1 -1 -0.5 0 X 0.5 1 -1 -1 -0.5 0 X 0.5 1 (a) 1 秒时的温度分布 (b) 5 秒时的温度分布 图 4 采用 C-N 格式计算得到的温度分布图 0 . 0 3 0.1 0 0.1 8 0.08 0.15 0.05 0.13 1 0.75 0.5 0.25 Y 0 -0.25 -0.5 -0.75 1 0.75 0.5 0.25 Y 0 -0.25 -0.5 -0.75 0.15 0.60 0.4 5 0.90 1 .0 5 0.3 0 0.6 0 -1 -1 -0.5 0 X 0.5 1 -1 -1 -0.5 0 X 0.5 1 (a) 1 秒时的温度分布 (b) 5 秒时的温度分布 图 5 采用全隐格式计算得到的温度分 - 4 - 

http://www.paper.edu.cn 3 结果及讨论 对于抛物型和椭圆型扩散方程中的源项进行线性化的处理，在数值分析中十分重要，因 为它直接影响到计算的收敛性和精确性。 本文通过系统地介绍源项线性化的处理过程，和给出具体算例，证明和展示了此方法的 可行性和实用性。 参考文献 [1] Patankar, S. V. Computation of Conduction and Duct Flow Heat Transfer. Innovative Research, Inc, 1991. [2] Patankar，S．V． Numerical Heat Transfer and Fluid Flow．New York，Hemisphere Publishing，1981. [3] Chai, J. C., Moder, J. P., and Karki, K. C., 2001, "A Procedure for View Factor Calculation Using the Finite-Volume Method," Numerical Heat Transfer, Part B, Vol. 40, No. 1, pp. 23-35. [4] Chai, J. C., Zhang, M., Moder, J. P., and Patankar, S. V., 2001, "Conduction Heat Transfer Calculations Using Structured and Unstructured Grids," ICHMT Symposium CHT'01 - Advances in Numerical Heat Transfer, Vol. 1, pp. 519-526. (Palm Cove, Cairns, Queens land, Australia). [5] Zhang ． M ． Modeling of Radiative Heat Transfer and Diffusion Processes Using Unstructured Grid．PhD．Dissertation，2000，Tennessee Technological University，USA [6] Kakac, S. and Yener, Y., Heat Conduction, Third Edition, Taylor & Francis, Publisher, 1993. [7] 商立英．非稳态导热问题在非结构化网格中的计算研究．南京理工大学硕士学位论文，2006 [8] M．N．奥齐西克 著，俞昌铭 译．热传导[M]．北京：高等教育出版社，1984 A Study of the Linear Source Terms for Diffusion Equations Zhang Min，Hu Wenbin，Li Lei，Xu Bin，Lu Xueshan School of Power Engineering，Nanjing University of Science & Technology，Nanjing (210094) Abstract Unsteady/steady state diffusion equations solved using a cell-based finite volume method in unstructured grid. The linear source terms were adopted. The two heat conduction examples including the different source terms were given. All above not only demonstrate the correctness of the method and program, but also provide valuable reference for calculation of many source terms. Keywords：source terms，linear method，diffusion equations - 5 -