线性控制系统工程.pdf-资料库

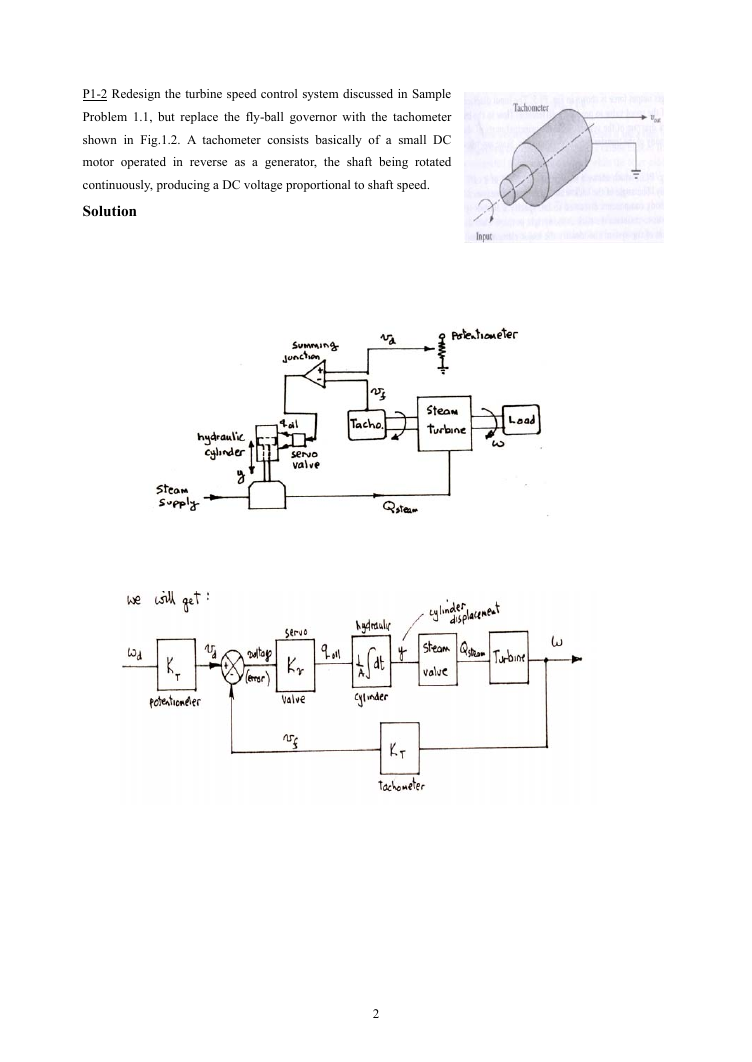
P1-2 Redesign the turbine speed control system discussed in Sample Problem 1.1, but replace the fly-ball governor with the tachometer shown in Fig.1.2. A tachometer consists basically of a small DC motor operated in reverse as a generator, the shaft being rotated continuously, producing a DC voltage proportional to shaft speed. Solution 2

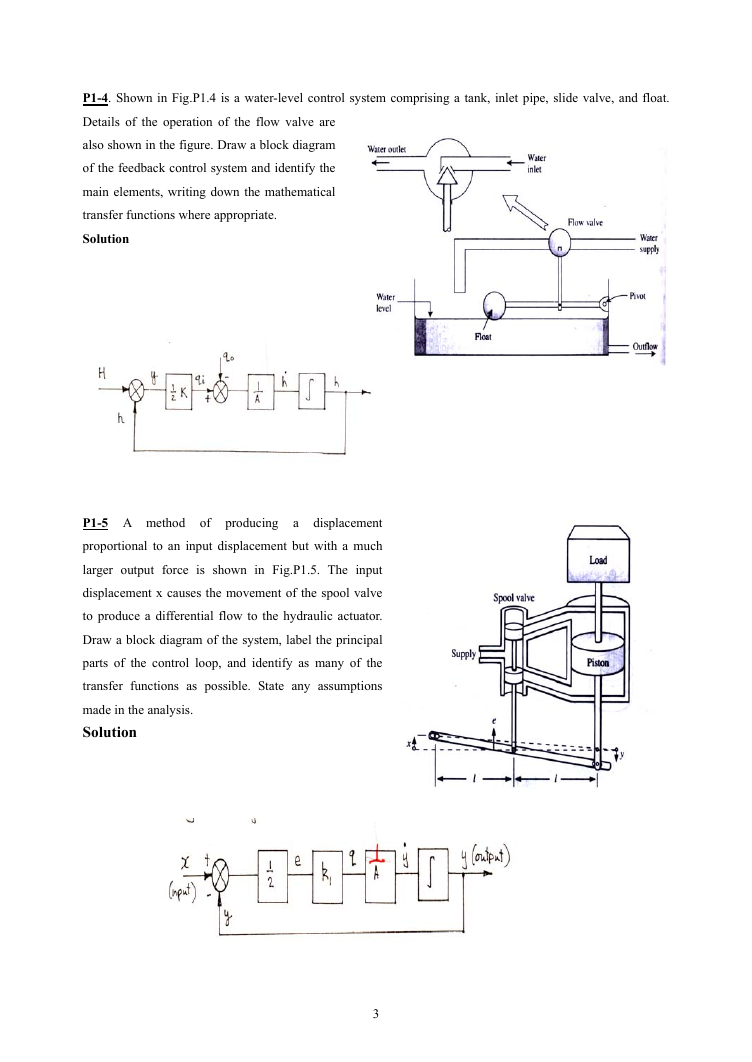
P1-4. Shown in Fig.P1.4 is a water-level control system comprising a tank, inlet pipe, slide valve, and float. Details of the operation of the flow valve are also shown in the figure. Draw a block diagram of the feedback control system and identify the main elements, writing down the mathematical transfer functions where appropriate. Solution P1-5 A method of producing a displacement proportional to an input displacement but with a much larger output force is shown in Fig.P1.5. The input displacement x causes the movement of the spool valve to produce a differential flow to the hydraulic actuator. Draw a block diagram of the system, label the principal parts of the control loop, and identify as many of the transfer functions as possible. State any assumptions made in the analysis. Solution 3

P2-1 A system unknown transfer function is shown in Fig.P2.1. If a unit impulse applied at the input produces at the output a signal described by the time function , determine the unknown transfer function. Solution )t(c t3e2 − t3e2 − => )t(c = = = C R 2 3s + P2-2. Find the solution of the differential equation + 2 xd 2 dt )t(z When + dx dt t2e −= x8 = dz dt + z3 and all other initial conditions are zero. Solution )s(Z = 1 2s + ⋅ 3s + 8s ++ 2 s = 1 2s + ⎛ ⎜⎜ ⎝ − Cs + 2 2 8s ++ ⎞ ⋅⎟⎟ ⎠ s C 1 = ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ 1 2s + − 11 2 + s − 1 2 ) 31 4 s( + ⋅ 1 10 ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ )t(y = e1.0 − t2 − e1.0 − 1 2 t ⎛ ⎜ ⎜ ⎝ cos 31 2 t − 23 31 sin 31 2 t ⎞ ⎟ ⎟ ⎠ P2-3 For the system shown in Fig.P2.3., determine the relationship between voltage and current, express this relationship in the form of a transfer function and determine the current as a function of time when the voltage is a step change from zero to 10V. Solution 1 sLR + + = /1 Cs Cs + RCs , + 1 2 LCs )s(Y = 10 s 2 LCs Cs + RCs = + 1 − 10 10 26 s − 10 ⋅ 10 + 6 − 3 1s + = 2 s + 10 3 s 10 6 + 10 )t(y = 10 − 2 2 3 − 500 t e sin( 3 2 1000 )t = .0 01154 ⋅ e − 500 t sin( 866 )t P2-8 For the system shown in Fig2.8 determine the closed –loop transfer function C/R. Solution C R = G HG1 + 1 1 ⎛ 1 ⎜⎜ +⋅ ⎝ G G 2 1 ⎞ =⎟⎟ ⎠ + GG 2 1 HG1 + 1 P2-9 For the single input system shown in Fig2.9, find the transfer function of output to input C/R. Solution GG 1 2 2 3 HGG1 + C R = HGG1 + 23 2 + GGG 21 + 2 3 HGG 121 => 32 HGG1 + 2 GGG 21 3 HGGGHGG 121 33 21 + 4

P3.2 Determine the output of the open-loop system G(s)=a/(1+sT) to the input r(t)=t. Sketch both input and output as function of time, and determine the steady-state error between the input and output. Compare the result with that given by Fig.3.7. Solution: )s(R)s(c = ⋅ e −=−= c r t Tt(a −+ a )sT1( + T/t− Te As ∞→t , ess −−= at t aT = a )sT1( +⋅ )t(c +−⋅= Tt(a Te T/t− ) for for 1a = 1a ≠ 2 = s ) T ⎧ ⎨ ∞ ⎩ P3.5 An open-loop first-order system is characterized b the transfer function )S(G = 1 s τ+ 1 , where the time s5=τ . Calculate the steady-state error when the system input is r(t)=1+6t. Confirm the result by constant is using the final-value theorem. Solution: By the superposition theorem, the system output c(t) could be considered as a sum of a step response and a ramp response. That is − 5/t e1( −− − 5/t ) = 30 − e5 − 5/t , yields (e =∞ ) 30 r c )t(e =−= e5t(6)1t6( +−⋅−+ ) By the final value theorem for Laplace’s transform, ⎛ 1) −⋅ ⎜ ⎝ )s(G1)s(R)s(C)s(R)s(E [ −⋅ 1 s − = + = 1 1s5 + ⎞ =⎟ ⎠ 5)s6( ⋅+ )1s5(s + ⋅ ] = 6( 2 s 5)s6(s ⋅+ ⋅ )1s5(s + ⋅ ⋅ 0 = = = 30 )t(e Lim s ∞→ )S(EsLim s → Lim t ∞→ P3.7 One definition of the bandwidth of a system is the frequency range over which the amplitude of the output signal is greater than 70% of the input signal amplitude when a system is subjected to a harmonic input. Find a relationship between the bandwidth and time constant of a first-order system. What is the phase angle at the bandwidth frequency? 1 = .0 707 ≈ or 1 =τω+ 22 b 2 2 2 Solution: 1 s τ+ 1 = =ω b /1 τ i.e. 1 22 τω+ b tan −=ω∠ )j(G − 1 ( −=ωτ ) tan − 1 )1( 45 °−= , phase lag is °45 at the bandwidth frequency. P3.8 Figure P3.8 shows the experimentally obtained voltage output of an unknown system subjected to a step input of +10V. Determine the transfer function of the system and locate its pole on the complex plane. Solution: System appears to be first order. So suppose the transfer function is as follow: C)s(G R /t τ−−⋅ e1(K10 K s τ+ , then )t(c ) = = = 1 From final value theory Lim t ∞→ )t(c = )s(CsLim s → 0 ⋅ = Now consider time constant， ⋅ sLim 0 s → t ⋅=τ 10 s K 1s +τ = V5.2K10 = ⋅ , hence K=0.25 1 1 K10 )t(c ⎞ ⎟ ⎠ − ⎛ − 1ln ⎜ ⎝ =1.4983 Matlab: K=0.25, c=[1.22, 1.84, 2.16, 2.33, 2.41], t=1:5, tao=t./(-log(ones(1,5)-C/10/K))*ones(5,1)/5 5

P4.1 Figure P4.1 shows a closed-loop feedback system with a second-order plant. Determine the damped natural frequency and damping ratio of the closed-loop response. 2 )s(C ω n )s(R 2 ζω+ ζω = 10 s6 + 16.3 2 s ω+ n n 2/6 = G GH + rad/s, =ω Hence => s = =ζ 10 /3 = + = = 3 1 s 2 2 n n ω=ω d n 1 =ζ− 10 ⋅ 9.01 − = 1 rad/s 10 2 10 = 3.0 10 P4.4 Calculate the required value of gain K shown in follow such that the closed-loop response of the system to a step input is limited to no more than 10% overshoot. Plot the closed-loop poles on the complex plane for the same value of gain. )s(C )s(R G GH + K sKs2 2 ω n ζω+ 12/2 = ζω = = + + = = 2 1 s s 2 2 n , 2 ω+ n n n = 1 ζ =ω 6.0=ζ By textbook fig.4.17, 10% overshoot is responding to 5 3 4j1 3 The closed-loop poles will be ω=ω =ς− ±−= 25 9 25 9 => 67.1 78.2 5 3 s 2 s2 K , , = = = = + + 1 0 s n d 2 6.01 − , K2 n =ω 2 = 4 3 = 33.1 or s ςω−= n ±−=ω± 33.1j1 j d the close-loop poles on P4.5 A unity-feedback control system has the forward-path transfer function G(s)=K/s(s+10). Find the closed –loop transfer function, and develop expression for the damping ratio and damped natural frequency in terms of K. Plot the complex plane for K=0,10,25,50,100. For each value of K calculate the corresponding damping ratio and damped natural frequency. What conclusions can you draw from the plot? )s(C )s(R K sKs10 2 ω n ζω+ ω+ = + + = 2 s s 2 2 2 n n 10 5 K Hence n =ω K and 2 ζω n = or =ζ Closed loop poles located at s ζω−= 1j ± 2 n n ±−=ως− 25Kj5 − P4.7 Prove that for an under damped second-order system subject to a step input, the percentage overshoot above the steady-state output (as shown in textbook Fig.P4.7) is a function only of the damping ratio ζ. By step response 1)t(c −= At the peak time, ζω− e n ζω− 1 t n 1 2 ζ− ζω− t n e sin( ) φ+ω t d sin( ω+φ+ω ) t ζω− t n e d cos( =φ+ω ) 0 d Tpd t d π ω d (tg ω=φ+ω ) t d / ςω n d φ= => ω = ,0 2, ππ ... => pT = ζω− n e π ω d PO = 1 2 1 ζ− sin( ω d π ω d =φ+ ) 1 2 1 ζ− e ζπ− 2 1 ζ− ζπ− 2 1 ζ− sin =φ e 6

P5.2 A second-order system is given by the transfer function )s(C )s(R = 10 9s2 + + = 10 9 2 2 9 9s2 + s + s Determine: a. damping ratio b. The damped and undamped natural frequency. c. Maximum peak modulus Mp d. The frequency at which Mp occurs. e. The bandwidth, defined as the frequency range over which the modulus does not fall more then 3db below the low-frequency (DC) value. f. The steady-state output for a unit step input. g. The location of the closed-loop poles on the complex plane. h. The rise time. i. The 2% settling time Solution: s/ 9/10 ω=ω 3/1=ζ n =ω ζω− 19 =− and rad3 83.2 22 rad ζω s/ , = = 1 2 n 2 n d ) ( = 77.1 , ω=ω p n 21 =ζ− 2 7 =2.65 n = 10 82 = , so 5 4 2 = M p = 2 ⋅ς 1 ζ− 2 , where r=ω/ωn 22 r x 2 − 1 3 = ++ x)9/4(1x2 = 29.4 3 07.77 + = 2 => x 2 − 01x)9/14( =− , =ω⋅=ω r 29.4 b n From .0M = 707 = r1( − 1 22 ) Squaring, and setting 81 x= ± 7 9 49 + 9 x = 7 = f. R(s)=1/s, e ss = )t(c lim t ∞→ = g. closed-loop poles for s2 4 ζ+ 2r ± , , gives 130 9 r 1s lim ⋅ s 0 s → , 9s2 + + ⋅ h. Rise time T r = 1 ω d i. 2% settling time T s ⎛ ⎜ ⎜⎜ ⎝ = 1 1 − tan −π ζ− ζ 4 ζω n = sec4 10 9 s s 2 2 = 10 9s2 + + 22j1 ±−= ⎞ ⎟ ⎟⎟ ⎠ 1 22 = ⋅ 91.1 rad = s68.0 P5.3 Consider each of the following closed-loop transfer functions. By considering the location of the poles on the complex plane, sketch the unit step response, explaining the results obtained: Solution: a. e ss b. )s(C )s(R = 20 s)(2s( + + )t(c = = lim t ∞→ )s(C )s(R = lim 0 s → 6 + )3s)(2s)(1s( + + )10 1s ⋅ s ⋅ 20 s)(2s( + + )10 = 1 Dominant time constant=1s, e ss = lim s 0 → 1s ⋅ s ⋅ 6 + )3s)(2s)(1s( + + = 1 7

c. Poles: = )s(C )s(R s −= =ω n from Fig4.7, 1s ⋅ s = e ss ⋅ lim 0 s → )s(C )s(R = d. Solving 2 s 9 3s ++ 5.0j5.0 ± ,3 =ζ PO = 9 3s ++ 10 + + 5s4 s 2 2 11 732.1/5.0 ,%35 c Δ = 3 + )5.0s)(5s4 =+ 0 gives =ζ sin =θ = 54.0 = 89.0 s( s 2 + 2 5 = = 289.0 05.4 s ±−= 2 j No overshoot, however, real axis pole will dominate with a time constant at 2s.ess=10/2.5=4 e. )s(C )s(R = Solving gives 1 2 + =+ s)(5s( + s2 5s2 + 2j1 s ±−= )5s2 + 0 =ζ sin =θ 1 5 = 45.0 The complex pair will dominate the real axis pole, ess=1/25=0.04 = f. )s(C )s(R Solving Solving 100 2 s)(13 2 s( + + s6 + + s2 13 s6 + s2 40 s12 + pair closer + )40 s12 + j23 s ±−= s j26 ±−= to im aginary axis will ,gives , gives Complex dominate those further away. ζ dom = 3 13 = 83.0 High damping, no or little overshoot, Steady state output=100/(13*40)=0.192 P5.6 Determine the magnitude of the first overshoot of an under damped, second-order system subjected to a unit impulse input. Plot a graph of this magnitude as a function of damping ratio ζ. Solution: )s(C )s(R = 2 ω n ζω+ 2 2 s ω+ 2 n n If R(s)=1 then )s(C = ω ζω+ n 2 n ) s( 2 ω+ 2 d )t(c let 2 n = ω ω d )t(dc dt ζω− t n e sin ω t d where ω=ω d n 2 1 ζ− = , 0 ζω− e n ζω− t n sin ω+ω t d ζω− t n e d cos =ω t d 0 hence =pT π φ at this time ,output M = ςω− n φ ω d ω ω 2 n d e sin ω d φ ω d This is a functi on of nω and ζ ,so plot M/ nω − ω= n ⎛ ⎜ exp ⎜ ⎜ ⎝ against ζ . 1 − tg ς 2 1 ζ− 2 ζ 1 − ς ⎞ ⎟ ⎟ ⎟ ⎠ 8

资料库

线性控制系统工程.pdf

相关推荐

课程资源

热门标签

最新资料