第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
朴素贝叶斯算法分析天气的好坏.docx
一、题目：朴素贝叶斯分类
二、引言
三、算法介绍
1.朴素贝叶斯分类的原理
2.根据上述分析，朴素贝叶斯分类的流程可以由下图表示（暂时不考虑验证）：
四、数据描述
五、实践过程
1.算法实现
2.测试结果
六、总结
一、题目：朴素贝叶斯分类
二、引言
大作业的任务是用朴素贝叶斯算法分析天气的和环境的好坏决定是否出门
打网球。首先构建训练集；再实现分类算法，通过分类算法对训练数据集的各个
特征属性分析，计算出各个特征属性的概率及每个特征属性划分对每个类别的条
件概率估计；然后输入测试数据，由算法给出分类结果，结果为“Yes”或“No”。
三、算法介绍
1. 朴素贝叶斯分类的原理
朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这
种方法的思想真的很朴素，朴素贝叶斯的思想基础是这样的：对于给出的待分类
项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类
项属于哪个类别。通俗来说，就好比这么个道理，你在街上看到一个黑人，我问
你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比
率最高，当然人家也可能是美洲人或亚洲人，但在没有其它可用信息下，我们会
选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。
朴素贝叶斯分类的正式定义如下：
。
为一个待分类项，而每个 a 为 x 的一个特征属性。
1、设
2、有类别集合
3、计算
4、如果
计算第 3 步中的各个条件概率：
1、找到一个已知分类的待分类项集合，这个集合叫做训练样本集。
2 、 统 计 得 到 在 各 类 别 下 各 个 特 征 属 性 的 条 件 概 率 估 计 。 即
。
，则
。
3、如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：
因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征
属性是条件独立的，所以有：
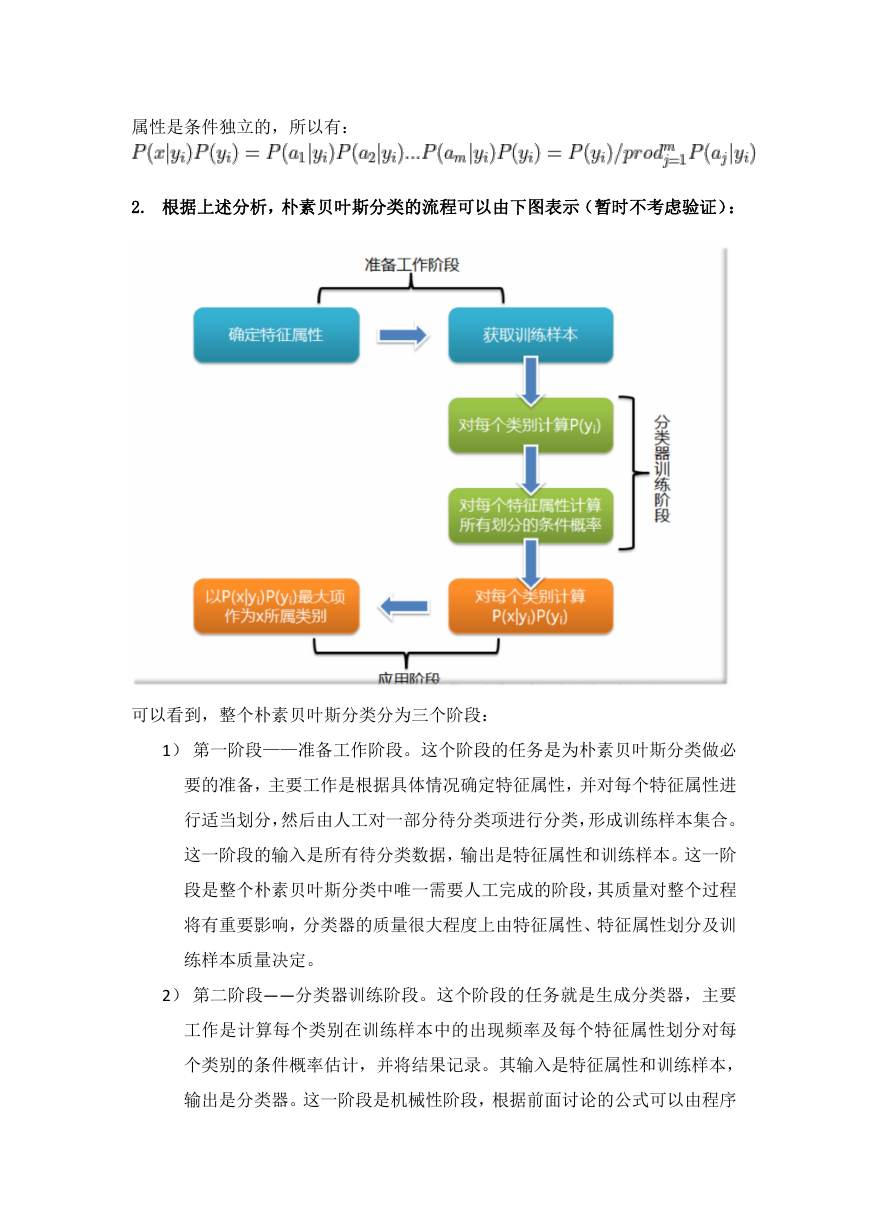
2. 根据上述分析，朴素贝叶斯分类的流程可以由下图表示（暂时不考虑验证）：
可以看到，整个朴素贝叶斯分类分为三个阶段：
1） 第一阶段——准备工作阶段。这个阶段的任务是为朴素贝叶斯分类做必
要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进
行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。
这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶
段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程
将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训
练样本质量决定。
2） 第二阶段——分类器训练阶段。这个阶段的任务就是生成分类器，主要
工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每
个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，
输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序
自动计算完成。
3） 第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行
分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。
这一阶段也是机械性阶段，由程序完成。
四、数据描述
训练数据集：由人工手动创建，输入到计算机程序的 txt 文件中。
Day Weather Temperature Humidity Wind PlayTennis
1 Sunny Hot High Weak No
2 Sunny Hot High Strong No
3 Overcast Hot High Weak Yes
4 Rainy Mild High Weak Yes
5 Rainy Cool Normal Weak Yes
6 Rainy Cool Normal Strong No
7 Overcast Cool Normal Strong Yes
8 Sunny Mild High Weak No
9 Sunny Cool Normal Weak Yes
10 Rainy Mild Normal Weak Yes
11 Sunny Mild Normal Strong Yes
12 Overcast Mild High Strong Yes
13 Overcast Hot Normal Weak Yes
14 Rainy Mild High Strong No
其中 Weather（天气）、Temperature（温度）、Humidity（湿度）、Wind（风
力）是四个特征属性，PlayTennis（打网球）是分类属性。
五、实践过程
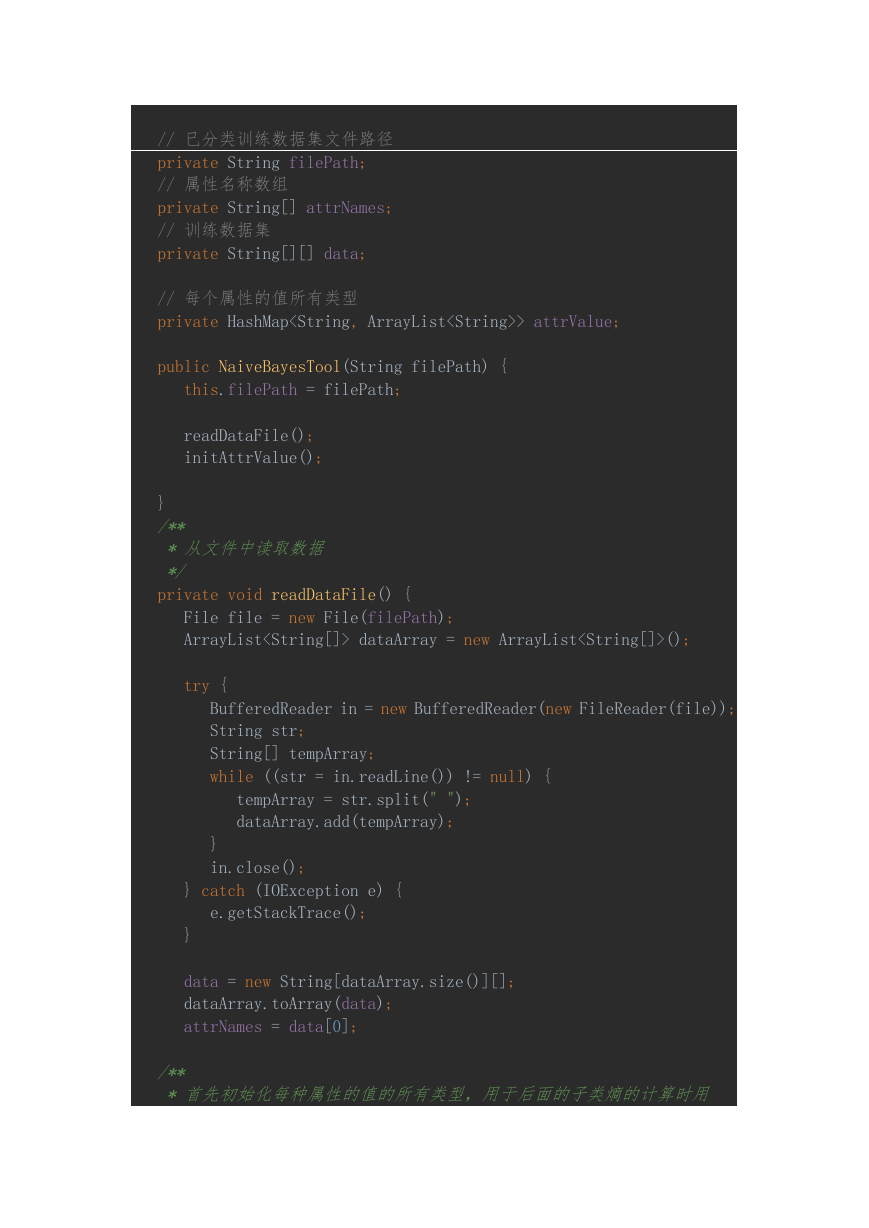
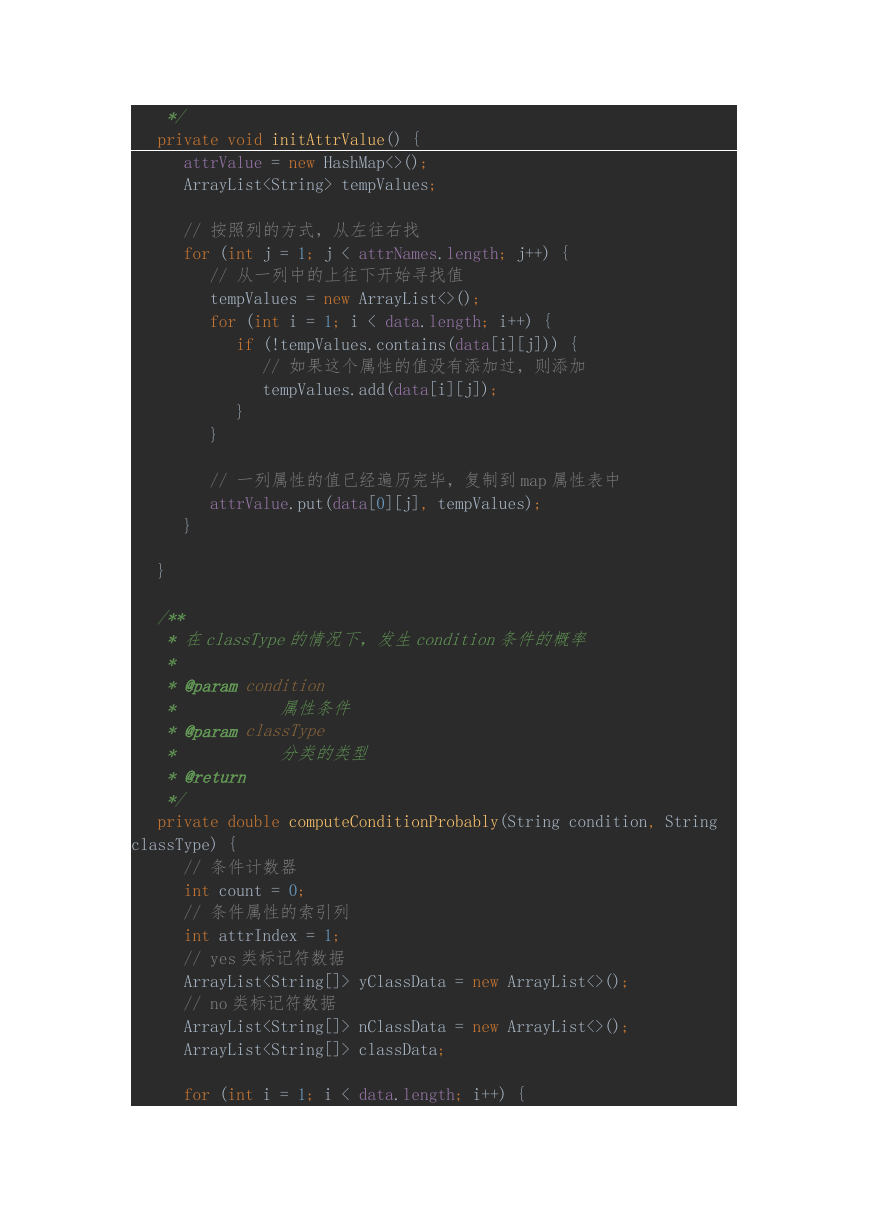
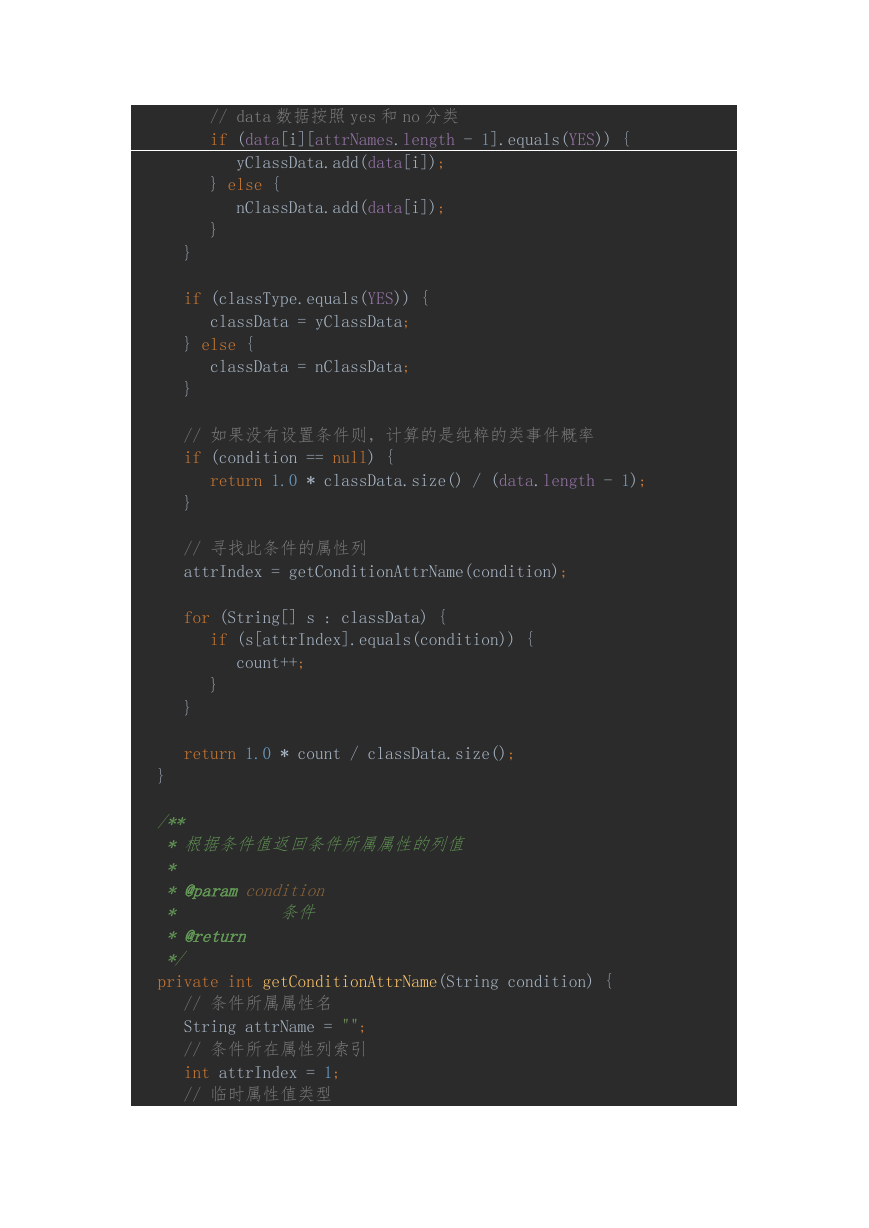
1. 算法实现
代码展示：
/**
* 朴素贝叶斯算法工具类
*/
public class NaiveBayesTool {
// 类标记符，这里分为 2 类，YES 和 NO
private String YES = "Yes";
private String NO = "No";
// 已分类训练数据集文件路径
private String filePath;
// 属性名称数组
private String[] attrNames;
// 训练数据集
private String[][] data;
// 每个属性的值所有类型
private HashMap> attrValue;
public NaiveBayesTool(String filePath) {
this.filePath = filePath;
readDataFile();
initAttrValue();
}
/**
* 从文件中读取数据
*/
private void readDataFile() {
File file = new File(filePath);
ArrayList dataArray = new ArrayList();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
data = new String[dataArray.size()][];
dataArray.toArray(data);
attrNames = data[0];
/**
* 首先初始化每种属性的值的所有类型，用于后面的子类熵的计算时用
*/
private void initAttrValue() {
attrValue = new HashMap<>();
ArrayList tempValues;
// 按照列的方式，从左往右找
for (int j = 1; j < attrNames.length; j++) {
// 从一列中的上往下开始寻找值
tempValues = new ArrayList<>();
for (int i = 1; i < data.length; i++) {
if (!tempValues.contains(data[i][j])) {
// 如果这个属性的值没有添加过，则添加
tempValues.add(data[i][j]);
}
}
// 一列属性的值已经遍历完毕，复制到 map 属性表中
attrValue.put(data[0][j], tempValues);
}
}
/**
* 在classType的情况下，发生condition条件的概率
*
* @param condition
*
* @param classType
*
* @return
*/
private double computeConditionProbably(String condition, String
分类的类型
属性条件
classType) {
// 条件计数器
int count = 0;
// 条件属性的索引列
int attrIndex = 1;
// yes 类标记符数据
ArrayList yClassData = new ArrayList<>();
// no 类标记符数据
ArrayList nClassData = new ArrayList<>();
ArrayList classData;
for (int i = 1; i < data.length; i++) {
// data 数据按照 yes 和 no 分类
if (data[i][attrNames.length - 1].equals(YES)) {
yClassData.add(data[i]);
} else {
nClassData.add(data[i]);
}
}
if (classType.equals(YES)) {
classData = yClassData;
} else {
classData = nClassData;
}
// 如果没有设置条件则，计算的是纯粹的类事件概率
if (condition == null) {
return 1.0 * classData.size() / (data.length - 1);
}
// 寻找此条件的属性列
attrIndex = getConditionAttrName(condition);
for (String[] s : classData) {
if (s[attrIndex].equals(condition)) {
count++;
}
}
return 1.0 * count / classData.size();
}
/**
* 根据条件值返回条件所属属性的列值
*
* @param condition
*
* @return
*/
private int getConditionAttrName(String condition) {
条件
// 条件所属属性名
String attrName = "";
// 条件所在属性列索引
int attrIndex = 1;
// 临时属性值类型
ArrayList valueTypes;
for (Map.Entry entry : attrValue.entrySet()) {
valueTypes = (ArrayList) entry.getValue();
if (valueTypes.contains(condition)
&& !((String) entry.getKey()).equals("PlayTennis")) {
attrName = (String) entry.getKey();
}
}
for (int i = 0; i < attrNames.length - 1; i++) {
if (attrNames[i].equals(attrName)) {
attrIndex = i;
break;
}
}
return attrIndex;
}
/**
* 进行朴素贝叶斯分类
*
* @param data
*
*/
public String naiveBayesClassificate(String data) {
待分类数据
// 测试数据的属性值特征
String[] dataFeatures;
// 在 yes 的条件下，x 事件发生的概率
double xWhenYes = 1.0;
// 在 no 的条件下，x 事件发生的概率
double xWhenNo = 1.0;
// 最后也是 yes 和 no 分类的总概率，用 P(X|Ci)*P(Ci)的公式计算
double pYes = 1;
double pNo = 1;
dataFeatures = data.split(" ");
for (int i = 0; i < dataFeatures.length; i++) {
// 因为朴素贝叶斯算法是类条件独立的，所以可以进行累积的计算
xWhenYes *= computeConditionProbably(dataFeatures[i], YES);
xWhenNo *= computeConditionProbably(dataFeatures[i], NO);
}
pYes = xWhenYes * computeConditionProbably(null, YES);
pNo = xWhenNo * computeConditionProbably(null, NO);
return (pYes > pNo ? YES : NO);
}
}
2. 测试结果
测试代码 1：
public class Test {
public static void main(String[] args){
//训练集数据
String filePath =
"D:\\ideaProjects\\bayes\\src\\NaiveBayes\\input.txt";
String testData = "Overcast Hot Normal Weak";
NaiveBayesTool tool = new NaiveBayesTool(filePath);
System.out.println(testData + " 数据的分类为:" +
tool.naiveBayesClassificate(testData));
}
}
测试结果 1：
测试代码 2：
public class Test {
public static void main(String[] args){
//训练集数据
String filePath =
"D:\\ideaProjects\\bayes\\src\\NaiveBayes\\input.txt";
String testData = "Sunny Hot High Strong";
NaiveBayesTool tool = new NaiveBayesTool(filePath);
System.out.println(testData + " 数据的分类为:" +
tool.naiveBayesClassificate(testData));
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
