学院计算机科学与技术专业计算机科学与技术 班 年级 学号 姓名 共 5 页 第 1 页 A 天津大学试卷专用纸 2013～2014 学年第 2 学期期末考试试卷 《形式语言与自动机》（A 卷 共 5 页） （考试时间：2014 年 6 月 12 日） 题号 一 二 三 四 成绩 核分人签字 得分 一、Regular Languages（50 分） 1. (5 分) Given the following state diagram of a DFA M1 (1) Please write out the formal 5-tuple definition of M1. (2) What is the language of M1, i.e., L(M1)? 2. (5 分) Give the state diagram of a DFA recognizing the following language {w | w has an odd number of a’s and ends with a b} 3. (5 分) Give the state diagram of an NFA with five states recognizing the following language {w | w contains the substring 0101 (i.e., w = x0101y for some x and y)} (Note that you cannot give a DFA.) 4. (5 分) Convert the following NFA to an equivalent DFA 

学院计算机科学与技术专业计算机科学与技术 班 年级 学号 姓名 共 5 页 第 2 页 A 天津大学试卷专用纸 5. (10 分) Convert the following regular expression to an NFA 6. (10 分) Convert the following DFA to a regular expression 

学院计算机科学与技术专业计算机科学与技术 班 年级 学号 姓名 共 5 页 第 3 页 A 天津大学试卷专用纸 7. (5 分) Prove that the following language are not regular 二、Context-Free Languages（30 分） { | } 9. (5 分) Given the following CFG 8. (5 分) Prove that the following language are not regular {wtw | w,t {0,1}+} Give the parse tree and the leftmost derivation for the string (a+a) a 10. (5 分) Given the following CFG Give the language generated by the above CFG. 21n0n

学院计算机科学与技术专业计算机科学与技术 班 年级 学号 姓名 共 5 页 第 4 页 A 11. (5 分) Give a CFG that generate the following language 13. (10 分) Convert the following CFG into an equivalent CFG in Chomsky normal form {w | the length of w is odd} 天津大学试卷专用纸 12. (5 分) Give the state diagram of a PDA that recognizes the following language {w | , that is, w is a palindrome} wwR

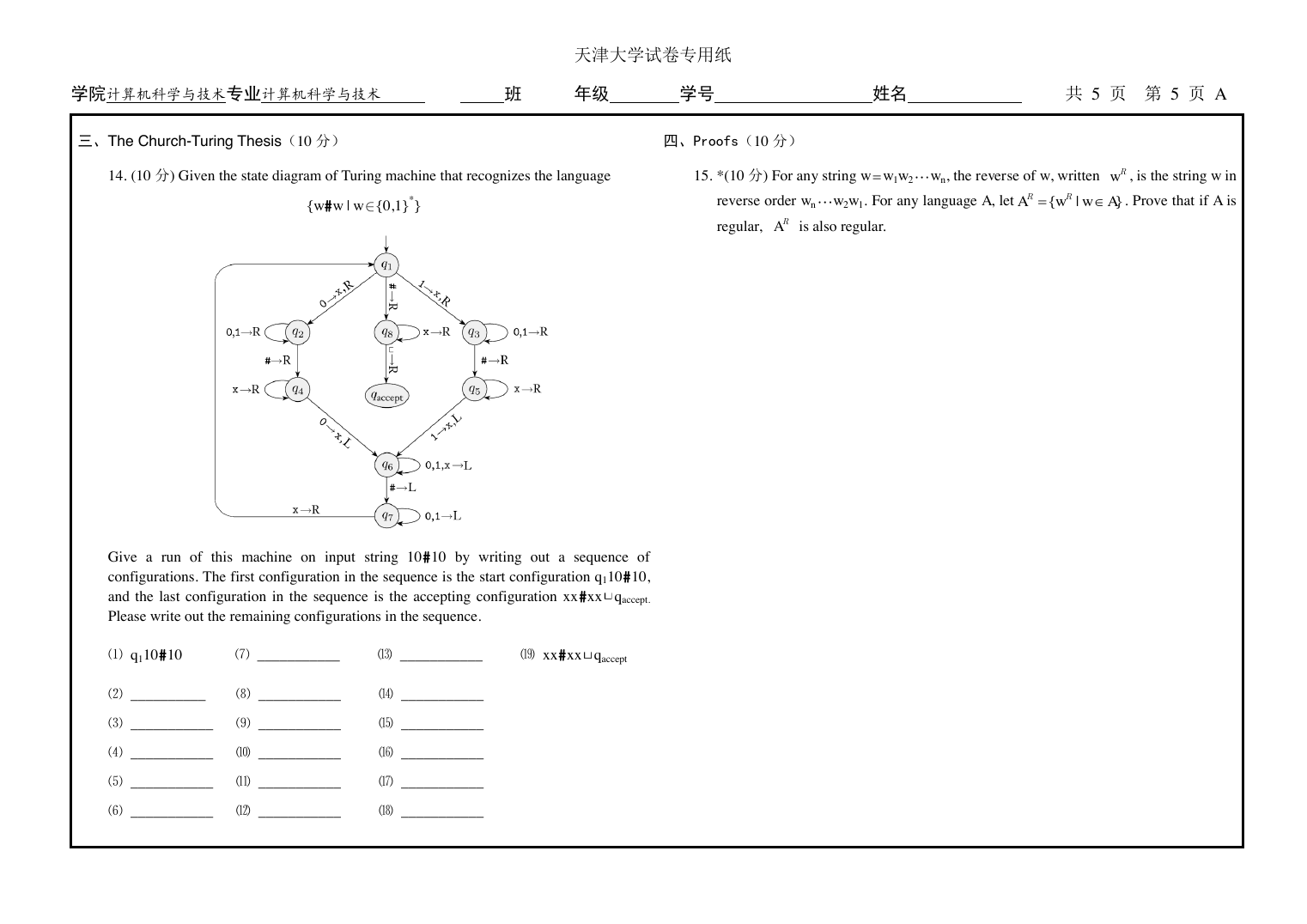
天津大学试卷专用纸 学院计算机科学与技术专业计算机科学与技术 班 年级 学号 姓名 共 5 页 第 5 页 A 三、The Church-Turing Thesis（10 分） 四、Proofs（10 分） 14. (10 分) Given the state diagram of Turing machine that recognizes the language 15. *(10 分) For any string w w1w2 wn, the reverse of w, written , is the string w in {w#w | w {0,1}*} reverse order wn w2w1. For any language A, let . Prove that if A is regular, is also regular. Give a run of this machine on input string 10#10 by writing out a sequence of configurations. The first configuration in the sequence is the start configuration q110#10, and the last configuration in the sequence is the accepting configuration xx#xx qaccept. Please write out the remaining configurations in the sequence. ⑴ q110#10 ⑺ ___________ ⒀ ___________ ⒆ xx#xx qaccept ⑵ __________ ⑻ ___________ ⒁ ___________ ⑶ ___________ ⑼ ___________ ⒂ ___________ ⑷ ___________ ⑽ ___________ ⒃ ___________ ⑸ ___________ ⑾ ___________ ⒄ ___________ ⑹ ___________ ⑿ ___________ ⒅ ___________ wR{|}AwwARRAR