IEEE Transactions on Power Delivery, Vol. 4, No. 2, April 1989
1401
NETWORK RECONFIGURATION IN DISTRIBUTION SYSTEMS
FOR LOSS REDUCTION AND LOAD BALANCING
M e w E. Baran
Felix F. Wu
Department of Electrical Engineering and Computer Sciences
University of California, Berkeley
Berkeley, CA 94720
Abstract - Network reconfiguration in distribution systems is realized by
changing the status of sectionalizing switches, and is usually done for loss
reduction or for load balancing in the system. In this paper, general for-
mulation and solution methods are proposed for these problems. In net-
work reconfiguration for loss reduction, the solution involves a search over
relevant radial configurations. To aid the search, two approximate power
flow methods with varying degree of accuracy have been developed. The
methods are computationally attractive and in general give conservative
estimates of loss reduction. For load balancing, a load balance index is
defined and it is shown that the proposed solution method for loss reduc-
tion can also be used for load balancing. Test results are included to show
the performance of the proposed method.
Keywords: distribution automation, distribution system operation, distri-
bution system planning, power flow analysis, combinatorial optimization.
I. INTRODUCTION
j
In primary distribution systems, sectionalizing switches are used for
both protection, to isolate a fault, and for configuration management, to
reconfigure the network. Fig.1 shows a schematic diagram of a simplified
primary circuit of a distribution system together with sectionalizing
switches.
'7
CB7
-
'
-
-
U - -
U"
1
ss 2
I
Figure 1: Schematic diagram of a primary circuit of a distribution system
In the figure. load points, where the distribution transformers are tapped
off from the primary circuit, is marked by dots, " 0 ". As also shown in the
figure, there are two types of switches in the system: normally closed
switches connecting the line sections (CB1 - CB6 ), and normally open
switches on the tie-lines connecting either two primary feeders (CB7), or
two substations (CB8), or loop-type laterals (CB9).
Distribution systems are normally operated as radial networks; how-
ever, configuration is changed during operation by changing the state of
some sectionalizing switches. For example, in Fig.1, switches CB7 and
CB8 can be closed and CB3 and CB6 can be opened to transfer load from
one feeder to another.
Especially with the introduction of remote control capability to the
switches, on-line configuration management become an important part of
A paper recommended and approved
88 SM 556-3
by the IEEE Transmission and Distribution Committee
of the IEEE Power Engineering Society for presentat-
ion at the IEEE/PES 1988 Summer Meeting, Portland,
Oregon, July 24 - 29, 1988.
Manuscript submitted
February 1 , 1988; available for printing
Xay 4, 1988.
distribution automation. An important operation problem in configuration
management is network reconfiguration. As the operating conditions
change, the network is reconfigured for two purposes: (i) to reduce the sys-
tem power loss, (ii) to relieve the overloads in the network. We will refer
to the first problem as network reconfiguration for loss reduction and the
second as load balancing. Another configuration management operation
involves the restoration of service to as many costumers as possible during
a restorative state following a fault. This problem is called service restora-
tion apd can be treated as a special load balancing problem. The network
reconfiguration for loss reduction can also be used in planning studies with
a different intelpretation; namely, to decide through which feeders the new
customers are to be supplied.
The early studies on the network reconfiguration were directed to the
planning stage [3-51. In planning, the main objective is to minimize the
cost of construction. An early work on network reconfiguration for loss
reduction is presented by A. Merlyn [6]. His solution scheme starts with a
meshed distribution system obtained by considering all switches closed
and then the switches are opened successively to eliminate the loops. An
equivalent linear resistive network model is used to determine the
branches to be opened. In a study done by Ross et al. [7], two different
search algorithms are giventor feeder reconfiguration. They developed
some indices to measure the degree of constraint violations and used them
to obtain a feasible point when the operation point is not feasible. These
indices are also used to check the optimality of the solution for power loss
reduction. Recently, Civanlar et al. [lo] presented a computatiody
attractive solution procedure for power loss reduction through network
reconfiguration. A simple formula was derived based on some simplifying
assumptions to calculate the loss reduction as a result of a load transfer
between two feeders.
In [7], a detailed recipe for service restoration is given by using the
indices developed for feasibility. In [8]. Castro et al. proposed simple
search techniques for sewice restoration and load balancing considering
data base and implementation requirements for on-line distribution auto-
mation applications. Castro and Franca [9] recently proposed modified
search algorithms for service restoration and for load balancing. A
modified Fast Decoupled Load Flow is used to check the operating con-
straints. Aoki et al. proposed more detailed search methods for service
restoration and feeder load balancing in [ll] and [12] respectively. They
consider the capacity and voltage constraints and use an approximate
power flow solution algorithm to determine the loads to be transferred
between the two feeders/transformers.
In this paper, we consider the network reconfiguration problem for
both loss reduction and load balancing. We follow the solution approach
proposed by Civanlar et al. However, here we introduce two different
methods, with varying degree of accuracy, to approximate power flow in
the system after a losd transfer between two substations, feeders, or
laterals. The methods make use of a new set of power flow equations
which have been developed specially for radial distribution feeders and
used in the capacitor placement problem [13]. We use these approximate
power Bow methods to estimate both loss reduction and load balance in
the system. Because reactive power flows are explicitly included in the
equations, the methods can also be used for systems that are not well com-
pensated.
The organization of the rest of the paper is as follows. A general for-
mulation of the problem is given in the next section and a general search
algorithm is presented in section 3. In section 4 and 5. the estimation
methods for loss reduction and load balance are given respectively. The
proposed methods have been programmed and tested and the results are
given in section 6. Conclusions are given in section 7.
0885-8977/89/04OO- 140 1 $0 1 .oO 0 1989 IEEE
�
1402
II. FORMULATION OF THE PROBLEM
In this section, the network reconfiguration problems for both loss
reduction and load balancing are formulated and their similarities are
pointed out.
2.1 Problem Statement
To simplify the presentation, we will represent the system on a per
phase basis and the loads along a feeder section as constant P,Q loads
placed at the end of the lies. We also assume that every switch is associ-
ated with a line in the system. For example, we assume that the system of
Fig.1 can be translated to an equivalent network shown in Fig.2.
ss1 m
Figure 2: One line diagram of a small distribution system
In the figure, solid branches represent the lines that are in service and con-
stitute the base radial configuration. Dotted branches (branches 20,2 1,22)
represent the lines with open switches.
The base network can be reconfigured by first closing an open
branch, say branch 21 in the figux. Since this switching will create a loop
in the system, (composed of branches 1,2,3,21, 11, 10,9,8,7, and 15), a
branch in the loop containing a switch has to be opened, say branch 7, to
restore the radial structure of the system. As a result of this switching, the
loads between the branches 7-1 1 will be transferred from one feeder to the
Other. We will use the same terminology used in [7] and call this basic
switching operation a brunch exchange between branches 21 and 7. In
general, as illustrated in the introduction, more complex switching
schemes are possible; we will simulate such cases by applying several
branch exchanges successively.
The load transfer between different substations can be simulated by
branch-exchange type switchings too. In this case, substation nodes (node
SSI and SS2 in the figure) will be considered as a common node although
they are not the same node. The methods to be presented in this paper can
handle both cases. This is an important property of the proposed methods.
The network rewnfiguration problems for loss reduction and load
balancing involve the same type of operation, namely the load transfer
between the feeders or substations by changing the positions of switches.
They only differ in their objective. Other factors, such as the voltage
profile of the system, capacities of the IinWtransformers, reliability con-
straints can be considered as constraints.
To state these problems as optimization pmblems, note that the
radial configuration corresponds to a "spanning tree" of a graph represent-
ing the network topology. Thus, we have a so-called minimal spanning
tree problem which can be stated as follows. Given a graph, 6nd a span-
ning tree such that the objective function is minimized while the following
constraints are satisfied: (i) voltage constraints, (ii) capacity constrains of
liies/transformers. (iii) reliability constraints.
This is a combinatorial optimization problem since the solution
involves the consideration of all possible spanning tms.
2.2 Power Flow Equations
To calculate the terms in optimization problem defined in the previous
section, we will use a set of power flow equations that are structurally rich
and conducive to computationally efficient solution schemes [13]. To
illustrate them, consider the radial network in Fig.3.
...... T'1k..'....-
(-*
i+ 1
i-1
i
mi
P,.Q,
-P;fQr-i
i+i*Qi+i
pn 'Qn
PL ,Qti
Figure 3 : One line diagram of a radial network
We represent the lines with impedances zl = r, + jx, , and loads as constant
power sinks, SL =PL + jQL .
Power flow in a radial distribution network canhe described by a set of
recursive equations, called D i s t F h branch equatwns , that use the real
power, reactive power, and voltage magnitude at the sendhg end of a
branch - Pi,Qi,Vi respectively to express the same quantities at the
receiving end of the branch as follows.
Pi,] =pi - ri - - "LI+I
p .2+Q 2
Vi'
VLl = Vi2 - 2(ri Pi + xi Q i ) + (r? + x?)-
P?+Qi'
Viz
(1.i)
(1 .iii)
Hence, if P o .Qo , Vo at the Erst node of the network is known or
estimated, then the same quantities at the other nodes can be calculated by
applying the above branch equations successively. We shall =fer to this
procedure as a forward update.
DistFlow branch equations can be written backward too. i.e., by using
the real power, reactive power, and the voltage magnitude at the receiving
end of a branch, P i , Q,, Vi to express the same quantities at the sending
end of the branch. The result is the following recursive equations, called
the backward branch equations,
Pl-l=Pl + f i T + P P ,
pl'2+Q,2
v,
(2.i)
(2.ii)
where, PI' = Pi + Pti , Q; = Q, + QL; .
Similar to forward update, a backward update can be defined: start
updating from the last node of the network assuming the variables
Pn , Qn , Vn at that point are given and proceed backwards calculating the
same quantities at the other nodes by applying Eq.(2) successively. Updat-
ing process ends at the first node (node 0) and will provide the new esti-
mate of the power injections into the network, PO .Qp
Note that by applying backward and forward update schemes succes-
sively one can get a power flow solution as explained in [131.
2 3 Calculation of the Objective Terms
.
Having a network model, now we can express the power loss and
measure the load balance in the system in terms of system variables.
For loss reduction, the objective is to minimize the total i2r losses in
the system, which can be calculated as follows.
(3)
This will be the objective function, cp of network reconfiguration for loss
reduction.
For load balancing, we will use the ratio of complex power at the
sending end of a branch, SI over its kVA capacity, Si"" as a measure of
how much that branch is loaded. The branch can be a transformer. a tie-
line with a sectionaliiing switch or simply a line section. Then we define
the load 'balance index for the whole system as the sum of these measures,
i.e.,
This will be the objective function, cb of load balancing.
As noted before, the two problems are similar. They both require the
same data (system parameters and load) and load flow calculation to
evaluate the objectives for a given network topology.
�
III. A SEARCH METHOD USING BRANCH EXCHANGES
The radial distribution network reconfiguration problems are formu-
lated as combinatorial, nonlinear optimization problems in the previous
section. The solution involves the selection, among all possible m s , of
the best feasible one (i.e., the one that has an operating point satisfying the
constraints and minimizing the objective). Of course, a search examining
all possible spanning trees will give the solution, but it would be computa-
tionally formidable; since, for one thing, the number of possible spanning
trees that can be generated by branch exchanges will be exhaustive for
practical size problems, and another, examining a spanning tree requires a
power flow solution of the corresponding system to determine
the associated objective. Therefore, an efficient search scheme needs to be
developed. In this section, we introduce a simple, heuristic solution
method to search over relevant spanning trees systematically by using
branch exchanges.
As exemplified in the previous section, branch exchanges can be
used to create relevant spanning trees starting from a base spanning tree.
In general, given a spanning tree To. we associate a loop with every open
branch in the network by considering as if the branch were closed. Fig.4
shows such a loop associated with open branch b . Branch exchange
creates a new tree by closing an open branch, @ranch b in the figure) and
by opening a closed branch in the loop (say branch m in the figure).
Figure 4: The loop associated with open branch b
The basic idea of the search scheme using branch exchanges is to
start with a (feasible) tree and then create new ones successively by imple-
menting one branch-exchange at a time. At each level, the branch-
exchange to be implemented is chosen to be the “best one“ (the one that
improves the objective function the most without any constraint viola-
tions) among all the possible trees (children) that can be generated f ”
the current incumbent spanning tree (parent) by branch exchanges. The
method can be described as an algorithm with the following steps.
Step 1: Given a feasible tree To (parent),
run a Power Flow to determine the operating point.
Step 2: Examine all the children of the parent as follows.
For each open branch b
- find a new candidate tree, T by
- identifying the loop
- deciding on the branch, m to be removed
- for the candidate W. T
- calculate the reduction in objective, Aq,,,,
Step 3: Sort the children (trees examined) by using Ach ‘s
Step 4: Find the tree T* which has the greatest Ach z 0
Step 5: If there is such a T’ ,
and satisfies the feasibility constraints.
then choose T’ as To and go to step 1; else stop.
We note the following comments about the search.
0 This search does not examine all the possible mes and hence the solu-
tion will be locally optimal.
0 Computational efficiency of this algorithm hinges on two things; the
selection of branch n to be opened, since it eventually effects the
number of searches to be performed, and the calculation of objective
terms, AC’S , for each calculation requires a new power flow solution.
Although the power flow solution can be obtained by DiszFfow
efficiently, nevertheless, it is desirable to be able to estimate the power
flows faster without actually running a DistFlow for each branch
exchange considered. This will reduce the DistFlow solutions to one
for each search level (iteration).
0 The estimated power flows a~ used in ranking open branches. There-
fore. emrs in estimated figures may lead to a different search than that
of using an exact power flow.
In the next section, two different power flow approximation methods,
with varying degree of accuracy, ye given for loss reduction. In section 5,
it is shown that these methods can also be used for load balancing.
1403
IV. APPROXIMATE POWER FLOW METHODS
FOR POWER LOSS ESTIMATION
In this section, we present two methods to determine the power flow in
a radial distribution system approximately. The methods will be used to
estimate the power loss reduction due to a branch exchange.
4.1 Method 1: Simplified DistFlow Method
Estimation of Power Flow
We can simplify the DistFlow branch equations, Eq.(l) by noting that
the quadratic terms in the equations represent the losses on the branches
and hence they much smaller than the branch power terms Pi and Qi .
Therefore, by dropping these second order terms we can get a new set of
branch equations of the following form.
Pi+l =Pi - PG+l
Q i + l = Q, - QG+I
V& = Vi2 - 2(ri Pi +xi Qi)
(5.i)
(5.ii)
(5.iii)
Since the network is radial, the solution for the simplified D i m o w q u a -
tions can be obtained easily; for a radial network of the type shown in
Fig.3, the solution is of the following form.
n
Q i + l =
QLk
(6.i)
(6.ii)
k=’+2
Vi:l = Vi2 - 2(ri Pi +xi Qi)
(6.iii)
We will call Eq.(6) simplifred DistFlaw equations and use them in this
section for power flow solution of a given network configuration.
The power loss on a branch can now be approximated as
where, we have used the fact that Vi2 = 1 p.u. Then the total system loss is
simply the sum of all branch losses, i.e.,
n-1
0 =
ri(P?+Q?)
p.u.
(8)
(7)
1 4
Estimation of Power Loss Reduction due to a Branch Exchange
Now consider the branch exchange between branches b (onginally
open) and m (originally closed) in Fig.4. As a result of the simplifying
assumptions made above, power flow will change only in the branches
constituting the loop shown in the figure. Let the branches in the loop that
extends between nodes 0 , . . . , k-1 and k be denoted by the set L and the
ones on the other side ( 0 , . . . ,n-1.n and k )by the the set R. Then. as
shown in Appendix A, power loss reduction due to this branch exchange
can be calculated as
U , - = 2p,(CrlPI - C . r ~ P ~ ) + 2 Q m ( ~ r ~ Q l
- Cr1Ql)
IcR
(9)
I s R
I P L
leL
-(P,’+Q:)[ C. r~ 1
I e R U
Eq.(9) is a quadratic function of the power transfer P,,, , Q,,, , i.e.,
U-h(P,,,,Q,,J = 2drp.P,,, + 2drq.Qm - tr. (P,’ + Q,’)
(10)
where, the coefficients drp , drq , tr are independent of the branch m con-
sidered and can be calculated by using only the original branch flows,
PI , Ql. The relationship between the loss reduction ALP and the power
transfer @,Q) is illustrated in Fig.5 assuming P and Q are continuous vari-
ables. In the figure, the circle defined by ALP-b = 0 divides th? P-Q plane
(P ,Q) > 0
into two regions such that for any point inside circle m b
(positive loss reduction, i.e. losses are reduced), and for any points outside
the circle U - b ( P , Q ) c 0 (negative loss reduction, i.e. losses are
increased).
�
1404
Figure 5 : Loss reduction as a function of power transfer
This property of Eq.(lO) can be used to avoid checking every branch
around the loop for branch exchange. Let us first consider the branch
exchange between branches b and k in Fig.4. and call it the nominal
branch exchange. The corresponding power transfer will be 9. Qk and
let this point (Pk ,Qk) be inside the circle on the P,Q plane in Fig.5. Then
the points corresponding to the other branch exchanges p i e (Pk-1,Qk-I)
in the figure) will be funher away from the origin on the P-Q plane than
(Pk ,e,) Since 9 - 1 > P k and
Qk . Therefore, We have the following
conclusions.
O E F i k c o then
ALPM < O
didate for branch exchange.
. I f W i k > O then
there is a branch in L that can be a candidate for branch exchange and
the branch to be opened should be the one that optimizes ALP-. This
can be checked by star$g
from branch k and searching the branches
backward in L until ALP*, is maximum.
I E L andhencethertisnobranchinL thatcanbeacan-
We have the following comments about the method.
0 This method is efficient computationally. Both the calculation of
power loss terms. ALP and identification of branches to be exchanged
I.equires only simple calculations.
0 Accuracy analysis of the method in Appendix B shows that a weak
bound on the error in estimating loss reduction around the loop,
ep =ALP -ALP is
U- 0 + ALP - U- I O ). However, when the loss reduction
where. fii and 6; denote the power losses on the branches in R and
L respectively after the branch exchange.
The e m r bounds inEq(l1) indicate that the estimate is conservative in
the sense that when the loss reduction is large (ALP- 3 0). e m r will
tend to be positive, (i.e., ALP- > 0 --). ALP -ALP- 2 0 ). Similarly
when the loss reduction is negative, e m r will tend to be negative, (i.e.,
figures are small, the e m r will be two sided. This e m r analysis shows
that there may be some "misses," (i.e., a branch e x c h g e with positive
loss reduction may be identified as the one with negative loss reduc-
tion) and there may be some "mislabeling," (i.e., a branch exchange
with negative loss reduction may be identified as the one with positive
loss reduction).
4.2 Method 2: Backward and Forward Update of DistFlow
Power Flow Update
The second method makes use of the backward and forward updates of
DistFlow, introduced in section 2. to update power flow around the loop of
a branch exchange. For the nominal branch exchange b-k of Fig.4. the
method comprises the following steps.
Step 1: Backward Update
Update the power flow mund the loop by backward update starting
from the nodes C and n of the loop and by canying out the power and
voltage updates separately (i.e., use Eq(2.i) and Eq(2ii) with original
voltages, Vi to update the powers, and use Eq42.iii) to update the vol-
tages). Let the updated powers be
and the voltage updates at the common node be $:
and $;
Step 2 Forward Update
Compare the voltage differences at node o (difference between V, and
rid,, $;).
If the voltage difference is too large (larger than a
predefined value. Emu), go through a forward update to ducf,the>mr
as
(this time starting from the common node o and using V, , P d , P,
initial, given values and applying the forward update). Let the updated
powers be
pi".di", i=ok+l,. . . ,k ; pii",Q,", i=on+l,. . . ,n
(13)
Step 3: Correct the Power Estimate at the Coqmo?,Node
P k , P, and P k , FR" as power
use the difference b e t w ~ ? the
mismatches and c o m t P, and Pok by adding them the mismatches.
i.e.,
1" P& = + (p; -PJ
.."
; P, 4; + (P, - P, )
Details of development of this algorithm is given in Appendix C.
Note that backward and forward update constitutes an itemtion of
power flow solution using DistFlow branch equations. Here., we exploit
the method by localizing it to the loop of branch exchange and performing
a special iteration. Therefore:
(14)
L"
A.
the method is computationally more. efficient than a full power flow,
0 accuracy of the method will mainly depend on load transfer P k , Qk .
Calculation of Power Loss Reduction
For power loss estimation, note that
P o k -Fo; = w k + w L ; P,
(15)
where, ALPp and ALPL represent the power loss reductions on the R and
L sides of the loop respectively. Therefore, the total power loss reduction
can be approximated as
L
= (Pok - Pok) + (P, - F:)
A d = U
-Pon =-@k
+ u R
+ U
(16)
A "
L n
0
R
V. LOAD BALANCING WITH BRANCH EXCHANGES
When the general search algorithm introduced in section 3 is used for
load balancing, the calculations will be similar to that of the loss reduction
case. The only difference will be in the calculation of the objective; for
load balancing. we need to estimate the value of the new objective, load
balance index, cb for every branch exchange considered during the search.
The objective, given by Eq.(4), can however be calculated by using
the two approximate p w e r flow methods introduced in Sec.IV - the
simplified DistFlow method and the forward and backwardupdate method,
because both of the methods give the approximate power flows in the sys-
tem following a branch exchange. Once the new power flow in the
branches, P,' , Qi are estimated then the new load balance index can be
computed by employing Eq.(4), i.e.,
P? + Q?
Cb =z-
s,-Z
When the two methods are compared for load balancing, simplified
DistFlow methad seems more attractive because of the following reasons.
0 Since the index of load balance is relative, the accuracy of simplified
DistFlow method should be ade@mte.
0 Simplified DistFlow provides a quick and c ~ d e estimate of the power
flows without requiring data on network parameters.
W. TESTRESULTS
The proposed solution method Bas been implemented in Fo~tran-77.
The approximate power flow methods described in k . W , (M1) -
simplified DistFlow. and (M2) - backward and forward updates of Dist-
Flaw. are used to guide the search In addition, exact power flow method,
DistFlow is also used as another method (M3), to check the accuracy of
M1 andM2. The test d t s for loss reduction will be presented here to
illustrate the performance of the proposed method.
The test system is a hypothetical 12.66 kV system with a 2 feeder subs-
tation, 32 busses. and 5 looping branches (tie lines). Me system data is
given in Table 1 together with the voltage profile of the base configuration.
The total substation loads for the base configuration 5084.26 kW and
�
2547.32 kvar. The system is not well-compensated and lossy (the total
loss is about 8% of the total load). A lossy system is selected because the
loss reduction is expected to be appreciable.
In the test runs, the constraints mentioned in Sec.II are not imposed.
In fact, the voltage profile of the base system configuration is lower than
the usual lower limit of 0.9 pa.; which shows that the system is not well
configured. Also, it is assumed that every branch in the system is avail-
able for branch-exchange.
A summary of the test run is given in Table 2. In the table, each row
cormponds to a branch exchange. Branch exchanges are d e w by a pair
of numbem in second column. The other columns labeled, M1. M2. M3
correspond to searches guided by methods M1. M2. M3 respectively. The
row after a search level, row six for example. shows the branch-exchange
chosen based on the ordering of the loss reduction figures obtained in that
search level.
1
1
35-11
35-11
35-11
37-28
brex
1
1
loss redudon in kW
M3
84.23
06.79
83.43
02.36
73.17
Table 2 Test Results
33-6
-01.71
f.6.
05.08
08.35
33-6
-02.05
05.92
17.82
03.00
05.12
33-6
-02.67
06.00
18.30
03.06
05.22
lscarch I branch I
level
M1
67.70
05.34
66.30
01.6 I
61.31
M2
77.89
06.64
77.25
02.32 I
70.15
bout
33-6
34-14
35-7
I 36-32 I
37-28
br-tx
6-7
34-14
1 1 1 i3 1
1 ;I. 1 37r
1
1
1
1 ;I. 1 37r
1
I 11-10 1 m:76 I -W:90 I -01.04
I
/!!I
34-14
11-10
36-31
37-28
br-ex
6-7
34-14
-05.19
-00.65
-00.16
11.76
08.35
-06.42
-00.80
-00.19
13.63
05.12
I 4
-05.02
-05.02
-01.35
-01.35
-01.58
-01.14
-01.11
-0044
-01.33
-01 12
1
1
-05.16
-05.16
-01.42
-01.42
o7.m
o7.m
-07.07
m.82
-00.22
15.77
0522
01.39
01.39
36-31
36-31
36-31
37-28
37-28
1
6
28-27
40.92
-03.93
i. In the Erst search level, the loss reductions are big. they satisfy the con-
servative property discussed in Sec.IIl and the e m m in estimations are
small enough so that the same branch exchange is chosen by all three
methods. However, as we go down the search levels, the loss reduc-
tions get smaller and the difference between the two estimated values
becomes more. visible; while estimation figures of M 2 consistently
satisfy the conservative property and get closer to the exact values,
accuracy and conservative property of M1 weakens (estimation
becomes two sided). This is particularly true for estimates of branch
exchange 37-28.
1405
ii. The thnx methods lead to the same searches at the upper levels (up to
level 4). At level 4, while the searches with M2 and M3 converge to a
local optimum as expected, the search with M1, which uses less accu-
rate loss reduction figures, mislabels brancli exchange 37-28 (i.e., esti-
mates a negative loss reduction as positive), and performs two more
searches leading to the global optimum point. However, the two solu-
tion points have close objective values (total loss reductions at the
solution points of M1 and M2. M3 are 125 kW and 118 kW respec-
tivel y).
iii. Branch exchanges occur on the lower voltage side of the loop.
iv. The voltage profile of the system increases as the loss is minimized.
(the minimum bus voltage of the system raises f ” 0.88 p.u. to 0.92
P.U.).
The last two observations were used as heuristic rules in the search in [7]
and [lo]. However, the observations may not always be true; a counter-
example is given in Fig.6, where branch exchange 7-3 is a switching on
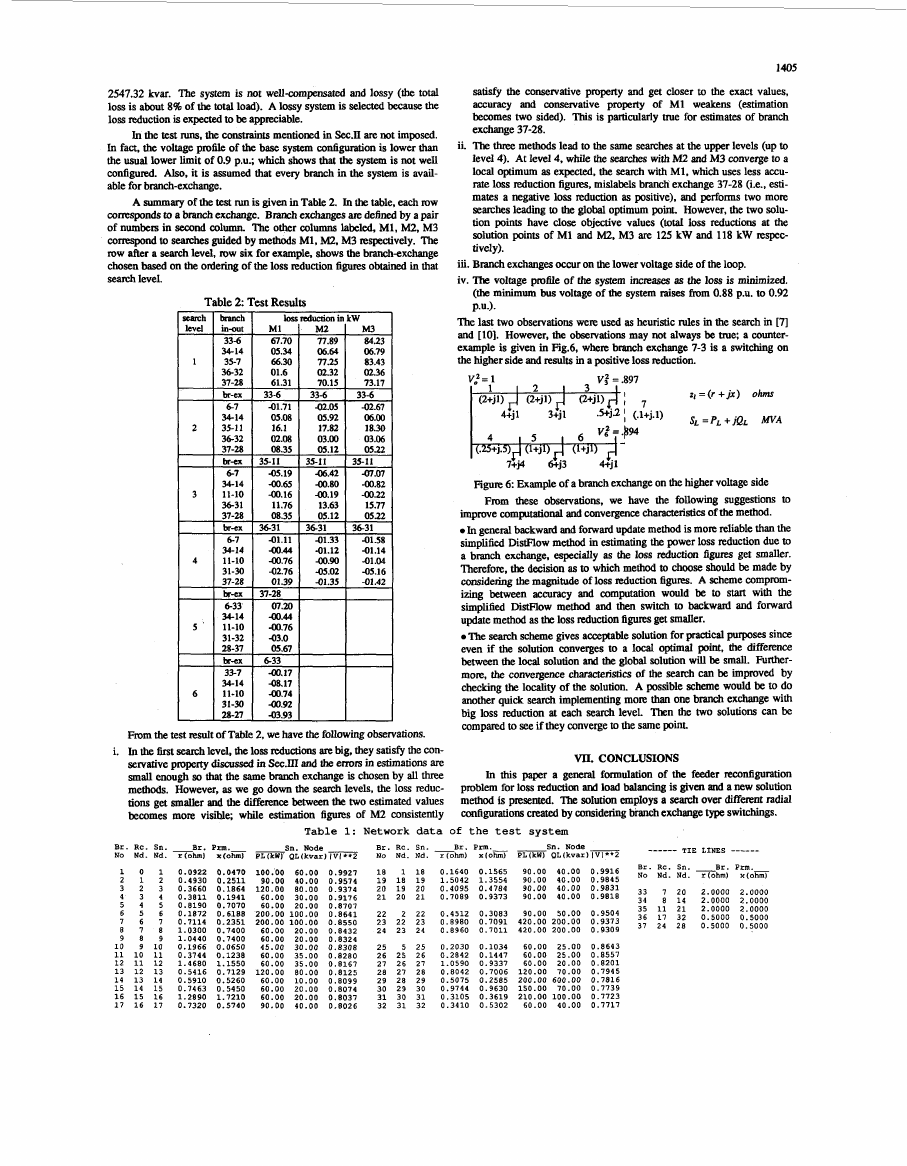
the higher side and results in a positive loss reduction.
v:=1
V i = .897
z , = ( r + j x ) ohms
sL =pL + jQL WA
figure 6: Example of a branch exchange on the higher voltage side
From these observations. we have the following suggestions to
impme computational and convergence characteristics of the method.
0 In general backward and forward update method is more reliable than the
simplified DistFlow method in estimating the power loss reduction due to
a branch exchange, especially as the loss reduction figures get smaller.
Therefore. the decision as to which method to choose should be made by
considering the magnitude of loss reduction figures. A scheme comprom-
izing between accuracy and computation would be to start with the
simplified D i m o w method and then switch to backward and forward
update method as the loss reduction figures get smaller.
0 The search scheme gives acceptable solution for practical purposes since
even if the solution converges to a local optimal point, the difference
between the local solution and the global solution will be small. Further-
more, the convergence characteristics of the search can be improved by
checking the locality of the solution. A possible scheme would be to do
another quick search implementing more than one branch exchange with
big loss reduction at each search leveL Then the two solutions can be
compared to see if they converge to the same point.
M. CONCLUSIONS
In this paper a general formulation of the feeder reconfiguration
problem for loss reduction and load balancing is given and a new solution
method is presented. The solution employs a search over different radial
configurations created by considering branch exchange type switchings.
Pm.- - Sn. Node -
Pm.- __ Sn. Node -
------
Table 1: Network data of the test system
r
.
Br. Rc. Sn. B
NO Nd. Nd. r(ohm] x(ohm) PL(kW) QL(kvar)IVI**2
1
1
0
2
2
1
3
3
2
4
4
3
5
5
4
6
6
5
7
7
6
8
8
7
9
8
9
10
9 10
11 10 11
12 11 12
13 12 13
14 13 14
15 14 15
16 15 16
17 16 17
0.0470
0.2511
0.1864
0.1941
0.7070
0.6188
0.2351
0.7400
0.7400
0.0650
0.1238
1.1550
0.7129
0.5260
0.5450
1.7210
0.5740
0.0922
0.4930
0.3660
0.3811
0.8190
0.1872
0.7114
1.0300
1.0440
0.1966
0.3744
1.4680
0.5416
0.5910
0.7463
1.2890
0.7320
100.00
90.00
120.00
60.00
60.00
200.00
200.00
60.00
60.00
45.00
60.00
60.00
120.00
60.00
60.00
60.00
90.00
60.00
40.00
80.00
30.00
20.00
100.00
100.00
20.00
20.00
30.00
35.00
35.00
80.00
10.00
20.00
20.00
40.00
0.9927
0.9574
0.9374
0.9176
0.8707
0.8641
0.8550
0.8432
0.8324
0.8308
0.8280
0.8161
0.8125
0.8099
0.8074
0.8037
0.8026
.
r
Br. Rc. Sn. B
NO Nd. Nd. r(ohm) X(0hm) PL(kW) QL(kvar)IVI**2
0.9916
18 1 18
0.9845
19 18 19
0.9831
20 19 20
0.9818
21 20 21
22 2 22
23 22 23
24 23 24
0.1640
1.5042
0.4095
0.7089
0.1565
1.3554
0.4784
0.9373
40.00
40.00
40.00
40.00
90.00
90.00
90.00
90.00
0.9504
0.9373
0.9309
0.4512
0.8980
0.8960
0.3083
0.7091
0.7011
90.00
420.00
420.00
TIE LINES ------
- Prm.-
Br.
r (ohm)
2.0000
2.0000
2.0000
0.5000
0.5000
x (ohm)
2.0000
2.0000
2.0000
0.5000
0.5000
Br. Rc. Sn.
No Nd. Nd.
33 7 20
8 14
34
35 11 21
36 17 32
31 24 28
25
5 25
26 25 26
27 26 27
28 21 28
29 28 29
30 29 30
31 30 31
32 31 32
0.2030
0.2842
1.0590
0.8042
0.5075
0.9744
0.3105
0.3410
0.1034
0.1447
0.9337
0.7006
0.2585
0.9630
0.3619
0.5302
60.00
60.00
60.00
120.00
200.00
150.00
210.00
60.00
50.00
200.00
200 .oo
25.00
25.00
20.00
10.00
600.00
70.00
100.00
40.00
0.8643
0 .E557
0.8201
0.7945
0.7816
0.7739
0.7723
0.7717
�
1406
To guide the search, two different power flow approximation
methods with varying degree of accuracy have been developed and tested.
The methods are used to calculate the new power flow in the system after a
branch-exchange and they make use of the power flow equations
developed for radial distribution systems.
Both accuracy analysis and the test results show that:
0 Estimation methods axe computationally very efficient and in general
give consenfative results. They also consider both real and reactive power
flows. Therefore. they can be used in searches to reconfigure a given sys-
tem even if the system is not well compensated and reconfiguring involves
load transfer between different subtations.
.The search method introduced in this paper, as well as in [7], [lo], [ll].
has the following appealing properties: it is not exhaustive, it is of order
m 2 (m is the number of open switches), and it involves about m power
flow solutions. Its convergence characteristics is acceptable although it
does not guarantee convergepce to the global optimum. However,
modifications to this basic search is proposed to improve its computational
and convergence characteristics whenever it is needed.
For load balancing, a load balance index is defined and it is shown
that the search and power flow estimation methods developed for power
loss reduction can also be used for load balancing since the two problems
are similar. Between the two estimation methods, the second - simplified
DistFlow method, seems to be more appropriate for load balancing
because of the relative nature of load balancing concept.
Acknowledgements
This research is supported by TUBlTAK-TURKEY and by National
Science Foundation under grant ECS-8715132.
REFERENCES
Distribution Systems, Westinghouse Electric Corp., East Pittsburg,
PA, 1965.
"Bibliography on htribution Automation" IEEE Transactions on
Power Apparatus and Systems, vol. PAS 103. June 1984, pp. 1176-
1182.
T. Gonen, A. A. Mahmoud and H. W. Golbum, "Bibliography of
Power Distribution System Planning", IEEE Transactions on Power
Apparatus andSystems, vol. PAS 102, June 1983, pp. 1178-1787.
D. I. Sun, D. R. Fanis et al., "Optimal Distribution Substation and
Primary Feeder Planning via the Fixed Charge Network Formula-
tion", IEEE Transactions on Power Apparatus and System, vol.
PAS 101, March 1982. pp. 602-609.
E. Lakervi and J. Partenen, "Linear Voltage Regulation and Loss
Calculation Methods for Low Voltage Network Design", IEEE Tran-
sactions on Power Apparatus ~ n d Systems, vol. PAS 103, Aug.
1984, pp. 2249-2253,
A. Merlin and H. Back, "Search for a Minimal-Loss Operating Span-
ning Tree Configuration in Urban Power Distribution Systems",
Proc. of5 th Power Systems Comp. Con., Cambridge, U.K., Sept.
1-5,1975.
D. W. Ross, M. Carson, A. Cohen, et al., "Development of Advanced
Methods for Planning Electric Energy Distribution Systems", DE0
final report no SCI-5263, Feb 1980.
C. H. Castro, J. B. Bunch, and T. M. Topka, "Generalized Algo-
rithms for Distribution Feeder Dep1oyn;ent and Sectionaliiing",
IEEE Transactions on Power Apparatus and System, vol. PAS 99,
MarCh/April1980, pp. 549-557.
C. A. Castro Jr. and A. L. M. Franca, "Automatic Power Distribution
Reconfiguration Algorithm Including Operating Constraints", Proc.
of IFAC on Electric Energy Systems, Rio de Janeiro, Brazil, 1985.
[lo] S. Civanlar, J. J. Grain&r,-and S. H. Lee. "Distribution Feeder
Reconfiguration for Loss Reduction", IEEE PES Winter Meeting,
Feb. 1987, paper no: 87WM 140-7.
111 J K. Aoki, H. Kuwabara, T. Satoh, and M. Kanezashi. "An Efficient
Algorithm for Load Balancing of Transformers and Feeders by
Switch Operation in Large Scale Distribution Systems", IEEE PES
Summer Meeting, 1987, paper no: 87SM 543-2
[12] K. Aoki, T. Satoh, M. Itoh, et al., "Voltage Drop Constrained Res-
toration of Supply by Switch Operation in Distribution Systems",
IEEE PES Summer Meeting, 1987, paper no: 87SM 544-0
[13] M. E. Baran, and F. F. Wu, "Optimal Sizing of Capacitors Placed on
a Radial Distribution System", presented at IEEE PES Winter Meet-
i n g , Feb. 1-6,1988, paper no 8 8 W M 065-5
A. Estimation of Power Loss Reduction due to a Branch Exchange
by Simplified DistFlow Method
APPENDIX
TO calculate the power loss reduction due to a branch exchange, we
need to estimate new branch flows after the switching around the loop
which is defined by the branch exchange. Note that the branch flows
before. the switching are known.
First consider the nominal branch exchange between branch b (on@-
nally open) and k (originally closed) of Fig.4. By simplified DistFlow
equation of (6). branch flows around the loop, Pi ,Qi will change by
Pk , Qk amount, i.e..
P:=Pi -P&
P ; = P i + P k
Q ; = Q ~ - Q ~ i c L
Q,'=Qi+Qk
i e R
(a1.i)
(a.13)
For the general case - branch exchange between branches b and m, it
can easily be verified that the branch flows around the loop will change by
P , , Q, , i.e.,
P,'=P~-P,,,
P;=Pi+P,,,
Q ; = Q ~ - Q ,
Q;=Qi+Q,,,
(a.2.i)
(a2.ii)
Now we can calculate the real power loss reduction due to branch
exchange b-m as follows. By Eq.(8), the original total power loss on L
and R sides of the loop will be
i c L
i e R
OL = B d P ? + Q t 2 ) OR = CrdP?+Q?l
ISL
I
d
(a.3)
These terms can be updated after the branch exchange by using the
updated power flows. P( , Q;. Let the updated loss terms be L F ~ ,G;.
Then the real power loss reduction. ALP-b, due to branch exchange b-m
will be
ALP-^ = ALP~+AL& = (OL-O~)+(LJsI-O~)
(a.4)
When the loss terms QL .OR are substituted in above equation and the
terms are rearranged, power loss reduction can be written only in terms of
original branch flows, Pi .Qi as in Eq.(9).
B. Accuracy Analysis of Simplified DistFlow Method
We will derive the relation between the actual loss reduction, ALP and
the estimated value, ALP- due to a branch exchange by simplified DistFlow
method in two steps; first power loss reduction along a radial network will
be studied, then these results will be used to evaluate the power loss reduc-
tion around the loop of a branch exchange.
Power Loss Reduction on a Radial Network
Consider the radial network shown in Fig.3. As noted before, such a
network represents one side, say side R , of the loop of a branch exchange.
Let the power change at the end of the network due to branch exchange be
w,, , AQ,, > 0.
Lets first comider the change in voltage profile as a result of change of
power at the end node n, Af, , AQ,,. A good esdmate can be obtained by
using the simplified DistFlow equations of (6). From Eq.(6), the change in
branch power will be
U. 1 - p : - p .
i =O, ..JI 0.1)
AQi = Q / - Q i =AQ.
=Af n
- t
Assuming V i = V, , change in voltages can be obtained by Eq.(6.iii) as
k=o
kco
0.2)
Therefore, the voltage profile along the network will drop with an increas-
ing magnitude towards the end of the network, i.e.,
'AV. SAV,,-lS ...
where, ALPi-,,, = ALPi,,
(pi + P~)' + (e! + QLi12
(pi + pli12 + (ei + e,)*
+ri[
1
The last term in 0.6) is due to the loss reduction on branch i , ALPi . Con-
sequently, the terms - ALP;,, , - ALQi, represent the actual loss reduction
between nodes i and n and have the following property.
Vi2
Vi2
0.6)
0 d ALP,,-l, S . . . S ALP.,.
These terms are of second order, i.e.,
; 0 5 ALQ,-l,, 5 . . . 5 ALQ,,
0.7)
l A P m l > lALf';,,I
; IAQe.l~IALQi,,I i = O J ,..., n-1 0.8)
Now consider the loss reduction on the network. Power loss reduction
ALPl can be calculated as
on line I ,
ALP1 =LP,-LP;
=r, -- v:
f'? + Q?
(PI + U n + -I,)'
r'
+ @I + AQn + MQ1.m 1'
V;2
0.9)
The simplified DistFlow method estimates this quantity as
U I =PI -P;= rl (f'? + Q?) - rt [(PI + APn)z+ (Q, + AQ.)2] 0.10)
Combining Eq.0.9) and Eq.0.10) will give
ALP1 =
1
Vl
- -LP1'+ &PI
1
Vl2
r1 [(Pl+AP,$+ (Ql+AQm)']
1
where, &!PI = -{
Vi
-- 71 [(Pt+dp,+ALPt,,)2+ (QI+AQ.+ALQ~,)~I) 5 0
1
V?
0.12)
Eq(b.12) indicates that 6Lpl represents the extra loss reduction due to
correction terms ALPI, and ALQl,, and it is of second order, i.e.,
16Lpl I << IALPI I . Dropping these second order terms, Eq.0.11) can be
bounded as
Since the total loss on the section is the sum of branch losses, the
bound for the whole section will be
where, f? and fz represent aggregated voltages, i.e..
Therefore,
By letting
V,2Sf. as a result of a power
change at the end of the network, AP,, , AQ. > 0, by using simplified Dist-
Flow equations in two different ways. Fist, as it is done in the Appendix
B. by assuming that Vi = V, and by using the simplified forward voltage
equation of Eq.(6.iii). Then the voltage drop can be calculated as
Second, by assuming Vi = V,, and by using the simplified
(AV:-.)f
backward equations V,ll = V: + 2(r,P,'+ x, Q,'), and calculating
the
comsponding voltage change as (AV,'-)b
It can be shown that
these two estimates are equal to each other, Le,
=AV,'.
=-AV:.
=
(AV,'-,,,,'
6.3)
The results indicate that a good estimate of voltage change at the ter-
minal nodes n and k can be obtained by canying out the voltage update
separately from the power update, while performing the backward update
and comparing the voltage difference at node o (difference between V, and
the updated Vb). If the difference is too large ( larger than a predefined
value, PX), one may go through a forward update to reduce the e m r (this
time starring from the common node o and using V.,@L,&, as initial,
given values and applying the forward update).
We use scheme 3 as the second method of updating the power flows
around the loop of a branch exchange.
Mesut E. Baran received his B.S. and M.S. form Middle East Technical
University, Turkey. He is currently a Ph.D. student at the University of
Califomia, Berkeley. His research interests include distribution and power
systems, optimization, system theory, and control theory.
Felix F. Wu received his B.S. from National Taiwan University. M.S.
from the University of Pittsburgh, and Ph.D. from the University of Cali-
fornia, Bekeley. He is a Professor of Electrical Engineering and Com-
puter Sciences at the University of California, Berkeley.
�













 2023年江西萍乡中考道德与法治真题及答案.doc
2023年江西萍乡中考道德与法治真题及答案.doc 2012年重庆南川中考生物真题及答案.doc
2012年重庆南川中考生物真题及答案.doc 2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc 2020年四川甘孜小升初语文真题及答案I卷.doc
2020年四川甘孜小升初语文真题及答案I卷.doc 2020年注册岩土工程师专业基础考试真题及答案.doc
2020年注册岩土工程师专业基础考试真题及答案.doc 2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc 2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc 2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc 2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc 2012年河北国家公务员申论考试真题及答案-省级.doc
2012年河北国家公务员申论考试真题及答案-省级.doc 2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc 2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc