logo资料库

simulink电动汽车动力模型和控制-dynamic_control_hev.pdf

发布时间：2022-06-20 发布人：admin 分类：说明书 资料大小：2.59M 资料格式：pdf 举报 版权申诉
第1页 / 共17页
第2页 / 共17页
第3页 / 共17页
第4页 / 共17页
第5页 / 共17页
第6页 / 共17页
第7页 / 共17页
第8页 / 共17页
资料共17页，剩余部分请下载后查看
    Authorized licensed use limited to: UNIVERSITY OF WINDSOR. Downloaded on July 22, 2009 at 15:02 from IEEE Xplore. Restrictions apply.
    . InverteriMotor Controller InverteriMotor Control Braking Control Motor Torque Motor Torque Delivered Traction Motor >ommand I -----+I I Motorhverter Motor Nonlinearities 1-q I I Efficiency Energy Recovered Inverter Load Current Vehicle Velocity Fig. I . Electric vehicle dynamic model. The driveline efficiency of the conventional powertrain portion of the HEV system can be improved by the inclusion of an auto- matic manual transmissioddry clutch driveline combination. Au- tomation of a manual transmission alleviates driver interaction with the clutch and gear shift lever required in a standard manual bansmissiodclutch combination, while providing near automatic transmission performance. This type of driveline, combined with the proper choice of “shift points,” and elimination of the torque converter (prevalent in automatic transmissions) can enhance fuel economy while mitigating emission effects. Such combinations of components, with an array of energy and power levels (as well as perhaps dissimilar dynamic proper- ties), yields a potentially difficult ensemble dynamic control problem. A powertrain dynamic model of such a complex pro- cess enables the development of a measure of performance and allows insight into the dominant dynamic effects in control law synthesis. Additionally, a powertrain model can be used to help determine optimum powerplantldriveline combinations, elimi- nating unnecessary vehicle builds. This article contains a de- scription of HEV dynamic models; many of the important dynamic control related issues are highlighted. The primary components presented include a vehicle driver, coordinated con- troller, a phenomenological model of a Spark Ignited (SI) Inter- nal Combustion Engine (ICE), variable field altemator, dynamic lead acid battery, dry clutch, automated manual layshaft trans- mission, brake system, complete vehicle longitudinal dynamics with tire-road interface characterization, and an ac induction mo- tor electric drive system. Also discussed in this article are automated manual layshaft conventional powertrain test results and simulations that demon- strate dynamic interactive effects and aid in the formulation of dynamic control laws for powertrain control. Presented also are simulations of the PHEV dynamic model, which demonstrate the added complexity of the electric powertrain dynamic interactive effects, the understanding of which is a precursor to dynamic control law synthesis. EV Powertrain System Vehicle Driver and Coordinated Control Generally, for all the vehicle configurations discussed herein, the driver model includes an implicit vehicle velocity controller, with driver velocity error and Propohonal-Integral-Denvatrve (PID) capability, and a collection of drive cycles to provide a ve- hicle input command. The vehicle driver model uses vehicle ve- locity feedback from the vehicle dynamics and a commanded vehicle velocity to generate braking to the brakes, and for an EV, a coordinated vehicle controller then provides motoring and re- generative commands to the motor controller for corresponding positive and negative motor torque. Perhaps command informa- tion is also provided to a clutch and transmission system when a manual or automatic manual transmssion is employed. A sche- matic representation of an EV dynamic powertrain without a gear changing transmission is shown in Fig. 1. Inverter/Motor Controller The traction motor and controller [lo], [11] extract power from the battery, or alternative energy storage device, and pro- vide torque to the driveline [ 121, [ 131, which in turn provides the EV motive power. Additionally, the traction motor and controller 18 IEEE Control Systems Brake Hardware Brake Command Hydraulic Brake System Brake Brake Torque Torque Vehicle Driver Accelerator Command Brake Command Vehicle Velocity Controller 1 - I 4 I Vehicle Dynamics Longitudinal Longitudinal Dynamics Dynamics Tire/Road Tire/Road Interface Interface Load Forces Load Forces Driveline Dynamics Dynamic Weight Transfer Battery Battery Dynamics Battery Nonlinearities Battery Efficiencies
    may be operated as a starter/alternator combination [14] or as a generator used to recover the vehicle kinetic energy dissipated during braking [ 1.51, [ 161. The traction motor and controller then provide power to the battery or altemative power source, and negative torque to the driveline, which in turn brakes the vehicle. The coordination of electric and hydraulic blending, during braking, is performed by the traction motor controller to meet the driver brake torque command. Compression braking torque, electric braking torque used to emulate the feel of engine drag present on an IC engine vehicle, is also determined by the trac- tion motor controller. All negative motor torque is reduced lin- early at low vehicle speeds where no energy can be recovered. Clompression braking torque allows braking to occur while re- covering the maximum energy, due to all braking being per- folrmed electrically. Traction Motor Dynamics The traction motor dynamic model [lo] represents the dy- namics of a specific field oriented controlled ac induction motor as described by the following equations: h,, = L, .iqs + L, .iqr h,, = L,T .id + L, .id, A,, =Lm.iqa +L;iq, h, = L, . i, + L, ' i, wlherei,,, iqr are d,q axis rotor current respectively, A; ids,iqs are d , q axis primary current respectively, A; L, are mutual induc- tance, H ; Lr, LJ are resolved rotor, stator inductance respec- tively, H; P is poles; Rr, Rs are resolved rotor, stator resistance reispectively, ohms; V,, Vqs are d, q axis primary voltage respec- tively, V; h,,,h qr are d, q axis rotor equivalent flux respectively, V-sec; h,, h , are d,q axis stator equivalent flux respectively, V-sec; o, is synchronous frequency, rps; or is rotor frequency, rps; &,is rotor acceleration, rps*; T,is electric motor torque, Nm. The traction motor torque delivered is modeled as a function of the motor dynamics, motor nonlinearities, and losses in both the motor and inverter as a function of motor speed. The traction motor torque limit is characterized by functions of the form: The inverter load current is a function of traction motor speed, torque delivered, and terminal voltage of the battery during mo- toring and during regeneration as: where elb is battery terminal voltage, V; Tmposdel is positive motor torque delivered during motoring, Nm.; q is motor and inverter combined efficiency. Battery The battery model is a lumped parameter dynamic character- ization of a lead acid battery [8], [14]. The open circuit voltage is a function of traction battery state of charge and empirical pa- rameters for lead acid batteries. The dynamic relationships be- tween battery voltage and current are modeled, including the polarization capacitive effect, incipient capacitance of the bat- tery, internal battery resistance, and terminal ohmic resistance. For example, V,, = 338.8.[0.94246 + 0.0.05754.( SOC)] + elb = zCh - R~ . ilh , R~ . . dt where C, is capacitive impedance, F; C, is polarization capaci- tance, F; Zlbis voltage drop due to_polarization capacitance, V; ilb is battery discharge current, A; R is battery intemal resistance, ohms; Rb is battery terminal resistance, ohms; SOC is battery state of charge, percent; V,, is battery open circuit voltage, V. Brake Controller The dissipation of kinetic energy during braking, by an electric or hybrid vehicle, can be recovered advantageously by controlling power electronics such that the electric traction motor behaves as a generator [ 121. The energy recovered during this process can be returned to the energy storage device for future use. A parallel braking system applies regenerative braking torque (to the driven wheels), in addition to hydraulic braking torque provided by the foundation braking system. Hydraulic brake torque is determined in the brake controller, based on HEV coor- dinated control commands [ 1.51, [ 161. Regenerative brake com- mands are predetermined as a function of master cylinder pressure in the traction motor controller and are based on PHEV coordinated control commands. In a series braking system, not illustrated here, integrated control exists between the brake con- troller and the traction motor controller [16], [17]. T, = Tared a,
    box input. In addition, the vehicle drivetrain receives hydraulic brakmg torque or other driveline loads, and vehicle velocity is determined via integration of the longitudinal equations of mo- tion. Rotational dynamics for each wheel, and halfshafts, and a representation of the forces acting on the vehicle, are modeled. Rotational wheel dynamics include wheel slip (skid), tireiroad surface adhesion coefficient, wheel tractive force as a function of dynamic weight transfer, road load torque for each wheel, and rotational wheel speed. Wheel slip (skid) is used to determine the tireiroad surface ad- hesion coefficient with a nonlinear analytic tireiroad surface inter- face model [l], [3], [17]. The tire model used for this study assumed a high road surface adhesion coefficient for dry pave- ment, because these are conventional driving conditions. The wheel tractive force as a function of dynamic weight transfer is the product of the road surface adhesion coefficient and the nor- mal force acting on the wheel: In calculating the normal forces acting on each wheel, the dy- namic weight transfer is modeled for each of both front and rear wheels in terms of the vehicle pitch and lever arms (wheel base) to the vehicle center of mass. The road load torque for each wheel is then determined from the wheel diameter and tractive force: The torques acting on the wheels include the halfshaft torque, Ts, road load torque, Tb, bearing friction torque, and the braking torque. Rotational wheel acceleration is obtained by the sum of the torque acting on the wheel divided by the wheel inertia. Wheel speed is obtained by integrating rotational wheel acceler- ation: The halfshaft model accounts for the torsional compliance be- tween the differential and wheel. The resulting halfshaft torque is applied to the wheel. The relations for shaft torque, and shaft com- pliance in terms of physical parameters are shown below: The four wheel tractive forces, aerodynamic drag, grade forces, and rolling resistance, describe the forces acting on the vehicle and are depicted below: Ft”, = Ft,, + Elr f Ft$ + Fdf - Fa,, - Fry - Fgrada . The aerodynamic drag on the vehicle is a function of vehicle velocity squared, air density, vehicle frontal area, and coefficient of drag, where the vehicle velocity is determined by solving €or vehicle acceleration and integrating over time: The rolling resistance force is a function of vehicle weight, roll- ing resistance coefficient, and vehicle speed: F,, = f, . W, .1.3558(1+ k, . V + k, . V’) The grade forces acting on the vehicle are a function of vehi- cle weight and grade angle: FgrOd, = W, .1.3558 sin0 . plied by the vehicle acceleration. The total forces on the vehicle equal the vehicle mass multi- In these equations, 4 is frontal area of vehicle,m2;Cd is aero- dynamic drag coefficient; Fa,, is aerodynamic drag force on ve- hicle, N; Fgrad, is grade force on vehicle, N; Frr is rolling resistance force on vehicle, N; f , is rolling resistance coefficient; ev is tractive force on left front wheel, N; c,r is tractive force on left rear wheel, N; e,, is total forces acting on vehicle, N; F,$ is tractive force on right front wheel, N; Jdq is differential inertia, kg.m2 ; Jfd-dg is final drive inertia on differential side, k g , m 2 ; J , is wheel inertia, kg .m2 K , is halfshaft stiffness, “/rad; K , is empirical constant; K2 is empirical constant; R,, is loss in shaft bearings, k g . m 2 i sec.rad ; R, is wheel radius, ft; Tb is brake torque, Nm; T is final drive output torque, Nm; TIoad is road torque, Nm; Tsis halfshaft torque, Nm; V is vehicle velocity, fd. m i sec2 ; W,is vehicle weight, lbf; y is air density, kg i m ; 8 is grade angle, rad; 0, is halfshaft displacement, rad; p(7r,lr,rf,y) is coefficient of friction on right rear, left rear, right front, and left front wheels respectively; 03 is wheel speed, radfsec; cofd is final drive speed on differential side, radfsec; ol, is left wheel speed, radisec; w, is right wheel speed, radisec. Series HEV Powertrain System Vehicle Driver and Coordinated Control A Series HEV (SHEV) powertrain may be achieved with the addition of an auxiliary power plant to the electric vehicle in power series connection with the traction battery and traction motor. In a “senes” configuration, the power unit interacts with the vehicle system controller and the rest of the vehicle electrical system, which includes the vehicle traction motor and other an- cillary loads such as power steering or air conditioning. The ve- hicle system controller provides a desired power command and a desired engine speed command to the SHEV system. Two or more control variables may be used to attempt to achieve the de- sired altemator power at a desired engine speed. In addition, the coordinated vehicle controller provides motoring and regenera- tive commands to the motor controller. A schmatic representa- tion of a series HEV is given in Fig. 2. Engine Dynamic Model The key exogenous control variable to the SI ICE engine sys- tem [9] is the throttle angle (or mechanical equivalent). For a die- sel engine it might be the fuel control system command. Control variables such as spark advance, Exhaust Gas Recirculation (EGR), and Air-to-Fuel ratio (AF), and variable geometry turbocharger on a supercharged power plant, are for this current representation considered to be precalibrated emission control 20 IEEE Control Systems
    ATR Brake System Vehicle Dynamics Brake Torque I Rotational Dynamics *Tire/Road lntetface Longitudinal Dynamics Driveline Dynamics ICommands - Accel and Brake Follow Specified 13rive Cycle High Fidelity Model of Brake Components IMC and Motor High Fidelity Induction Motor Provides Motoring Torque Regen Braking Torque No Pedal Torque t Inverter Load - - Strateav & Maximum Power Maximum Power Utilization Utilization Meet Emission Meet Emission Constraints Constraints Command Command b b Energy Storage Device Batteries Powerplant SI Engines SI Engines Turbine Turbine Diesel Diesel Speed Speed I *Variable Field - Fixed Field Fixed Field Variable Field 10 to 60 kW 10 to 60 kW temperature, KO; y is ratio of constant pressure to constant vol- ume specific heats. The changing flow area, Ae, is a function of the obstructing geometry presented to the flow field. For example, employing experimentally obtained engine pumping flow rate data for a cir- cular bore of approximately 34 mm the flow rate (kghr) may be given in terms of throttle angle (theta) in degrees as F ( e ) = c,(e)A(e) = 3.765 - 0.1058 e + 0.05479 e* . The manifold dynamic equations that result from using en- ergy balance and thermodynamic principles [8] are P . = -(Th,,, RY V -Tho)+ -Qm y-1 ‘ V where C,, C , is constant pressure, volume specific heats; m,,, is sum of manifold intake mass flow rates, kghr; riz, is sum of all outflow mass rates, kghr; Q, is rate of heat flow into the mani- fold, Jouleslsec; Tt is temperature of intake masses, deg; V is manifold volume, cm3. Mass and momentum balance are achieved by assuming uni- form temperature, pressure and density in each open thermody- namic volume as well as assuming a conservation of mass constituents where no chemical reactions take place. In some in- stances, a further simplified model is justified by assuming in- variant manifold temperature without loss of the dominant manifold filling effect. However, temperature effects should not be neglected when “cold” engine conditions, cold dense air Fig. 2. Series HEV dynamic model. variables. The throttle control law includes a variable gain PI (proportional plus integral) controller to provide a limited throt- tle command to the engine, based on commands from the vehicle driver controller. Included also in the throttle command control law are the Wide Open Throttle (WOT) operating logic and an engine Idle Speed Control (ISC) law. The throttle body is considered as a variable nozzle for air flow modeling. By considering one dimensional, steady, com- pressible, isentropic flow of an ideal gas, the equation represent- ing mass flow across a valve opening or orifice results in a quasi-steady relation. In terms of the throttle valve or cross sec- tional area, Ae, and pressure ratio, the mass flow rate through the valve is given by where where P, is downstream pressure, kPa; P, is upstream pressure, kPa; R is specific gas constant, atm .liter I gm .mole. K ; Tu is upstream October 1998 21
    charge, or evaporating and condensing fuel are important dy- namic issues. An estimation of mass flow rates out of the manifold is given approximately by a product of the engine speed, engine displace- ment, and volumetric efficiency, which in turn is resolved in terms of engine speed, intake temperature, manifold pressure, and exhaust gas pressure. Manifold mass flow rate egress is given in terms of manifold pressure and engine speed by an ap- proximate polynomial functional form . M = ---(OS22 N 1000 + O.OS553(-))(0.17P+ N 1000 0.00098P2), where M is speed density mass flow rate, kg/hr and N is engine speed, rpm. The engine torque developed at any time is a function of the mass rates (mass charge) or ratios of rates (mass constituents) that were sampled one engine induction event earlier. This breathing event is a crank angle synchronized relationship that is primarily dependent 011 engine speed. For a zero order extrapola- tion, the minimum delay in torque generation that results from ingestion of the manifold constituents is 180 crankangle degrees. For a four cylinder engine with a speed of N RPM, this is repre- sented by a propagation lag relationship with idealized delay T is 30/N seconds. A similar lag exists for the mixed A/F from the end of com- bustion to exhaust valve closure. In addition, a nonspeed depend- ent propagation lag, and some gaseous diffusion, is assumed to persist in the exhaust pipe before the A/F sensor location [18]. Representation of the A/F delays in an SI ICE is extremely im- portant as the torque response is highly sensitive to A/F tran- sients, including throttle input and fuel control system transients. The nonlinear structure for the A/F (Air/Fuel) system con- sists of an EGO (exhaust gas oxygen) A/F sensor in the exhaust pipe, with a time constant of the order of 70 ms, followed by a nonlinear (Nernst) rich/lean Signum function and a PI fuel com- mand control law [18]. An intake runner port fuel injector is as- sumed with a fuel rate output, and with fuel condensation and evaporation dynamics [ 191. The resulting system equations are . dm T -‘=rp~~-m~, ” dt m, = (1 - Tl)rifi + mi, , m is manifold fuel flow rate, kglhr; m t~ is injector fuel rate com- mand, kg/hr;nifL is injected fuel flow rate, kglhr;m is fuel evapo- ration rate, kghr; q is fuel accumulation parameter, = 0.25 sec; T~ is injector time constant, = 50 ms; 7, is condensation and evapo- ration time, = 0.5 sec. The fuel mass flow rate is combined with the throttle mass air flow rate to form the manifold A/F. This A/F is delayed by the in- duction breathing lag, preparatory to combustion torque genera- tion, followed by a combustion torque delay, a power-stroke to exhaust delay, and a plug stroke exhaust system delay that is de- pendent on the location of the EGO sensor. Torque generated from the combustion process is dependent on the ignition of a cylinder charge o f air, fuel, and residual gas, as well as other variables and parameters that influence combus- tion efficiency. Assuming a spark advance, EGR (exhaust gas recirculation), and fuel emission calibrated 1.8 liter engine, an approximate brake torque relationship is of the form T = q ( A l F , ( A / F ) 2 , M , M 2 , N ,..., N4, EGR). The rotational motion of the engine crankshaft is given in terms of the engine polar moment of inertia, angular accelera- tion, and the difference between the net torque generated by the engine and the load torque on the driveshaft. Thus, J,N = (30 / E)( T, - where the load torque may be the starter-alternator (S/A) load, clutch torque, air conditioning, power steering, or any driveshaft load and J , is engine flywheel inertia, kg . m ’. StartedAlternator The alternator model is empirically derived from data taken at several voltage, field current, and speed operating points. Using voltage, field current, and speed as inputs, the alternator current output is determined by functional relationships. This model rep- resents a three phase synchronous machine generating full wave rectified DC current [ 161. The starter portion of the StartedAlter- nator (S/A) is also empirically derived from data and dynamic simulation results [7]. It is depicted by a 1.4 kW ac motor directly connected to the voltage bus and geared to the ICE crank. The S/A system is controlled via on/off logic and field current com- mands to control the S/A torque input (or output) of the device. For an HEV application, the alternator may be assumet to out- put 70 amps over a voltage operating range from 200 to 380 Volts. The alternator output current can be represented as a func- tion of field current, speed, voltage and temperature where the al- ternator field current is a separate dynamic control component. The alternator output current approximation at a certain speed and varying output voltage is The field current can be represented as follows: The inductance and resistance vary with speed, load and interior alternator temperature. Here, I,,l is alternator output current, A; I , is alternator field current, A; Lfld is alternator field inductance, H; R, is alternator is alternator field voltage, V; V,,, is al- filed resistance, ohms; V,, ternator output voltage, V mail is alternator rotational speed, krpm. Series HEV Control A large ICE powerplant (approximately 60kW or more), could be employed to directly supply the demand power while using a scaled down battery for partial load leveling or as a direct power source during high power demand. In such a power source tradeoff the nature of the performance requirements, limitations on sensor and control mechanisms, and dynamic control law structure will likely change. The control objectives with a more powerful ICE/alternator and reduced traction battery system 22 IEEE Control Systems
    340 338 336 334 332 330 328 326 324 1000 \ 500 1 0 0 1 I I 15 5 10 Fig. 3. Series power unit control. might yield a load leveling or load following strategy [20]. In this instance, the combined powerplanthattery system would be the prime vehicle power source used to follow the desired vehicle pro- file while the battery power supply would be used to mitigate the traction motor transient demands to the ICE/altemator system. Simulation results for such a combination are shown in Fig. 3. In this simulation, the vehicle driver would like to follow the the first few active (non-idle) seconds of the Federal Urban Driving Cycle (FUDS). In the transient behavior depicted in Fig. 3, the driver’s input goes directly to the Induction Motor Control (IMC) of the traction motor and simultaneously to the thirottle command of the ICE. Until the ICE/alternator can achieve alternator “cut-in’’ (i.e., that speed at which there is a power output from the alternator), the traction motor draws power from the energy storage device which in this case is a low storage (small) battery pack. The combination of components thus illustrated would require a smaller battery pack and re- duced ICE by proper sizing and proration of power between the ICE and energy storage device. Simulations that include engine, alternator, battery, and trac- tion motor/driveline sizing and dynamic interactions, could be used to examine energy tradeoffs and transient tradeoffs by vary- ing control and sizing (kW output) between an alternator and bat- tery system as series power sources. For instance, for a small ICE-alternator-battery power source (about 25 kW), a system operating strategy could be such that the “Range Extender” (RE) is to be activated during estimated low battery State-of-Charge (SOC) and simply operates until a desired SOC [8], [20] has been achieved. There exists dynamic interaction among the ICE, alter- nator, battery and vehicle traction motor (drivetrain) such that en- Olctober 1998 23
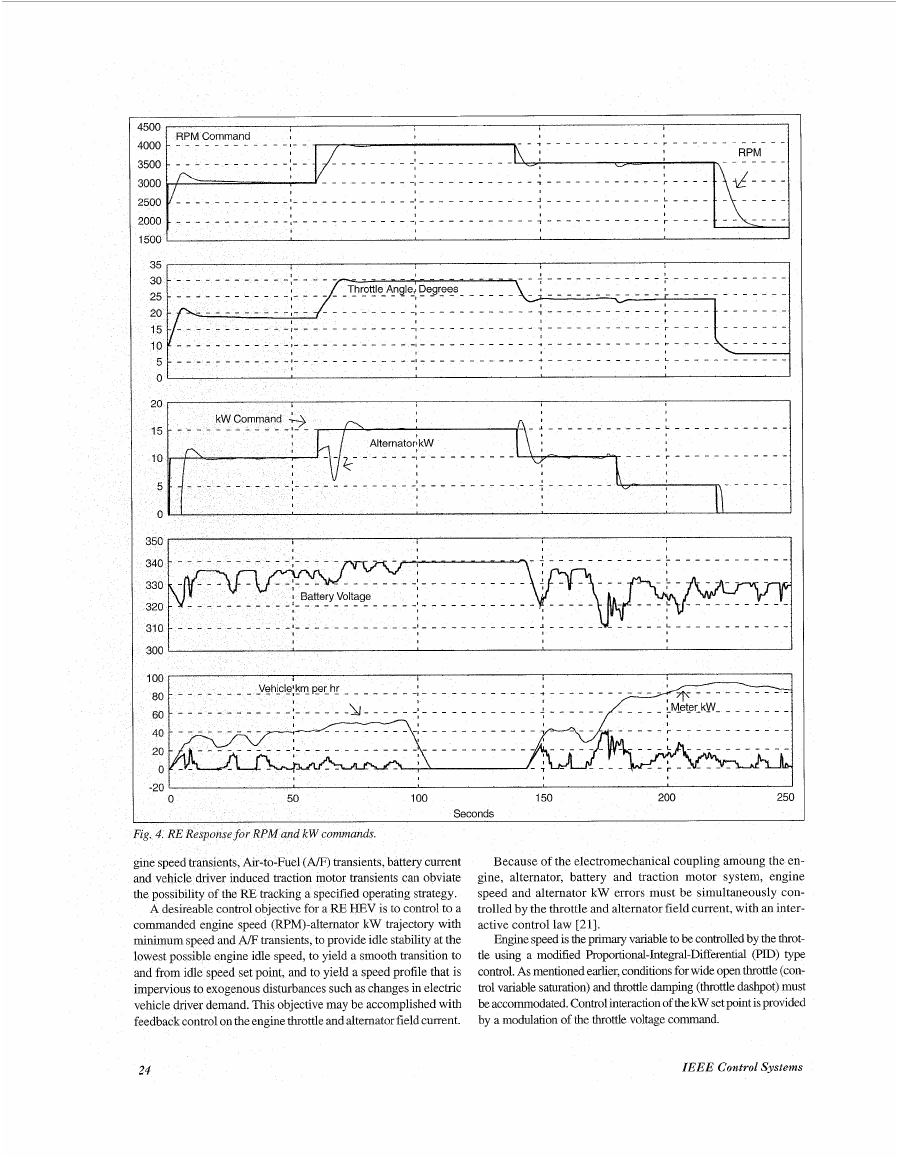
    ified operating strategy. A desireable control objective for a RE HEV is to control to a commanded engine speed (RPM)-alternator kW trajectory with minimum speed and A/F transients, to provide idle stability at the lowest possible engine idle speed, to yield a smooth transition to and from idle speed set point, and to yield a speed profile that is impervious to exogenous disturbances such as changes in electric vehicle driver demand. This objective may be accomplished with feedback control on the engine throttle and alternator field current. speed and alternator kW errors must be simultaneously con- trolled by the throttle and alternator field current, with an inter- active control law [21]. Engine speed is the pnmaq variable to be controlled by the throt- tle using a modified Proportional-Integral-Differentd (PID) type control. As mentioned earlier, conditions for wide open throttle (con- trol variable saturation) and throttle damping (throttle dashpot) must be accommodated. Control interaction of the kW set point is provided by a modulation of the throttle voltage command. 24 IEEE Control Systems
    分享到：
    赞 收藏

    相关推荐

    资料库

    大数据

    共收录841份资料，累计11个分类，关注成员有19位，主要包括：Matlab,统计分析,数据挖掘,Hbase,Hive,flink,kafka,spark,Storm,算法与数据结构,Hadoop

    热门标签

    Matlab 统计分析 数据挖掘 Hbase Hive flink kafka spark Storm 算法与数据结构 Hadoop

    最新资料