2003年全国大学生数学建模优秀论文.doc-资料库

jiajialin_2009-4566490-16359647956453306336.doc.pdf-第1页.png

第1页 / 共11页

jiajialin_2009-4566490-16359647956453306336.doc.pdf-第2页.png

第2页 / 共11页

jiajialin_2009-4566490-16359647956453306336.doc.pdf-第3页.png

第3页 / 共11页

jiajialin_2009-4566490-16359647956453306336.doc.pdf-第4页.png

第4页 / 共11页

jiajialin_2009-4566490-16359647956453306336.doc.pdf-第5页.png

第5页 / 共11页

jiajialin_2009-4566490-16359647956453306336.doc.pdf-第6页.png

第6页 / 共11页

jiajialin_2009-4566490-16359647956453306336.doc.pdf-第7页.png

第7页 / 共11页

jiajialin_2009-4566490-16359647956453306336.doc.pdf-第8页.png

第8页 / 共11页

C 题 SARS 的传播摘要本文首先采用抽样检测法对 SARS 早期的模型的合理性及实用性进行了评价，然后我们通过对传染病的共性及 SARS 的特性的分析。得出三个基本假设并且把人群理想化为三类（S 类，I 类，R 类），建立起基本的 SIR 模型，再对 SIR 模型中三类人群间的相互转化关系的分析，结合马氏链得出三种人群间变化率的矩阵 T，由于 SARS 的特性，可知，SIR 模型中的两个参数 a(t),b(t)是以时间为变量的函数。我们根据北京疫情的数据，通过多项式的数据拟合法分别得 a(t),b(t)的表达式，我们把 a(t),b(t)及 T 结合，从而建立出模型。由于医疗条件的逐步改善，必会研制出其疫苗。于是我们在不改变人群分类的情况下，增加了一个系数 c，（c 表示疫苗日成功接种率，由于在疫情期间，疫苗未能及时改良，故 c 为常数。）进一步完善了我们的模型。本文利用数学软件（Mathematica,Matlab）很好的实现了模型运算，并结合实际数据得出了各类人群与时间的关系图。从图中可以很好的反映出各类人群的变化规律，它们的变化规律与实际变化相吻合，从而证明了我们的模型基本符合要求。 1

一问题的提出严重急性呼吸道综合症，简称 SARS，是 21 世纪第一个在世界范围内传播的传染病。它对全球的经济和生活造成巨大的破坏，尽管目前疫情已得到控制，但对这种新冠状病毒及其流行规律的研究还刚刚开始，因此，有必要根据 SARS 流行的特点，建立数学模型预测其传染，从而采取措施预防和控制其发展。而建立该模型我们要综合各方面的因素才能使模型合理化。通过分析北京，香港和广东三地的受感染人数的变化规律，我们就可以对不二问题的分析同地区预测流行病的变化趋势提出以下模型假设。模型的假设： 1 将人群分为三类易感染者人数（疑似病例）：用 S 表示；病人数（已受感染者，即确疹者）：用 I 表示；移出者人数（包括“被治愈者”和“死亡者”）：用 R 表示 2 该地区人口不流动，疫情阶段无病原的输入和输出，设最初易感染者人数为 N，此时 I，R 均为 0。 3 被隔离人群完全断绝与外界接触，不再具有传染性。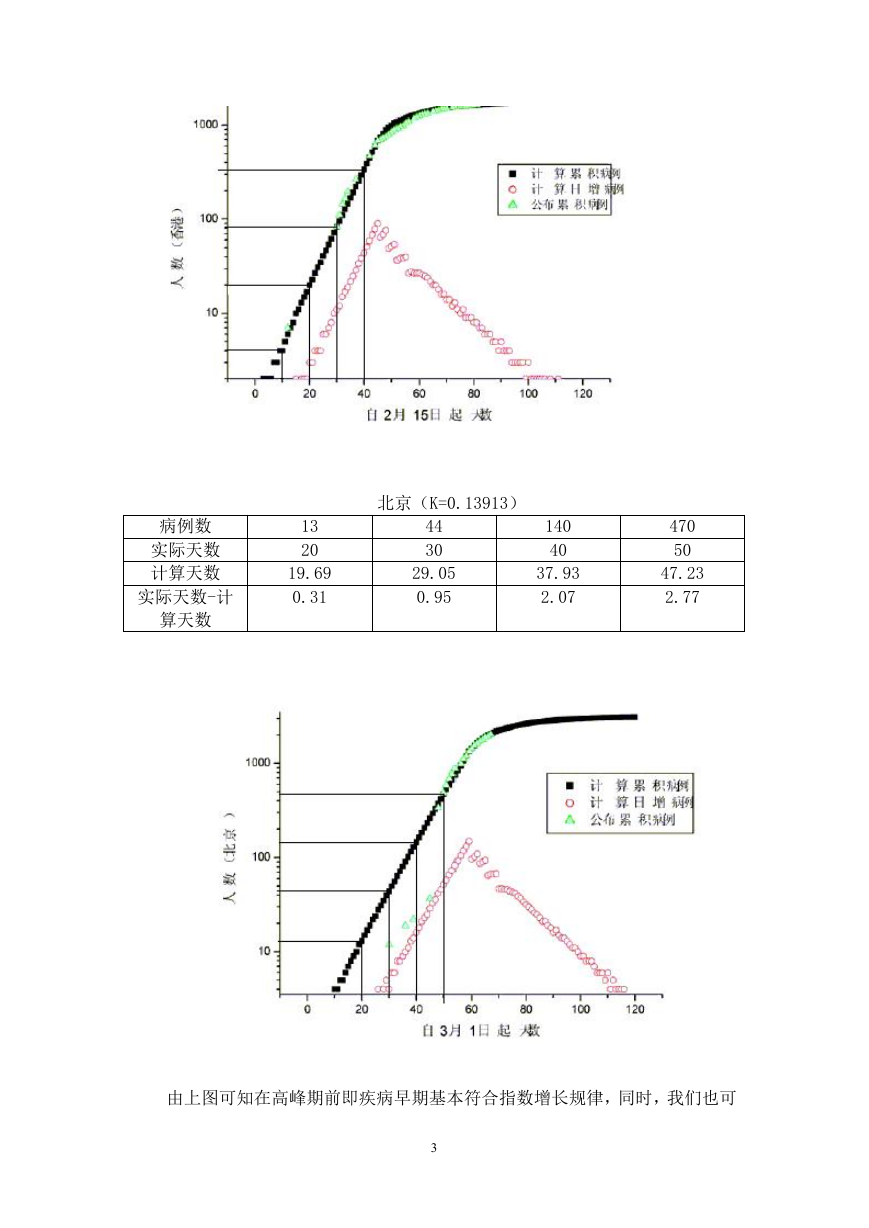问题一: 三模型的分析与建立对于附件 1 所提供的早期模型即 N（t）=N 0（1+K） t 在疾病初期应该有它的可参性。因为模型 N（t）=N 0 （1+K） t 是符合指数增长规律的。而对于这种传播疾病，由于社会来不急防备以及群众的不重视，使得 SARS 疫情基本上呈自然规律增长，这与香港的实际疫情拟合图基本一致。通过对香港和北京高峰前期的病例与天数的对应关系计算出的数据与实际基本吻合。见下图表：香港（K=0.16204） 4 病例数 10 实际天数计算天数 9.23 实际天数-计算天数 0.77 20 20 19.95 0.05 80 30 29.18 0.82 320 40 38.41 1.59 2

病例数实际天数计算天数实际天数-计算天数 13 20 19.69 0.31 北京（K=0.13913） 44 30 29.05 0.95 140 40 37.93 2.07 470 50 47.23 2.77 由上图可知在高峰期前即疾病早期基本符合指数增长规律，同时，我们也可 3

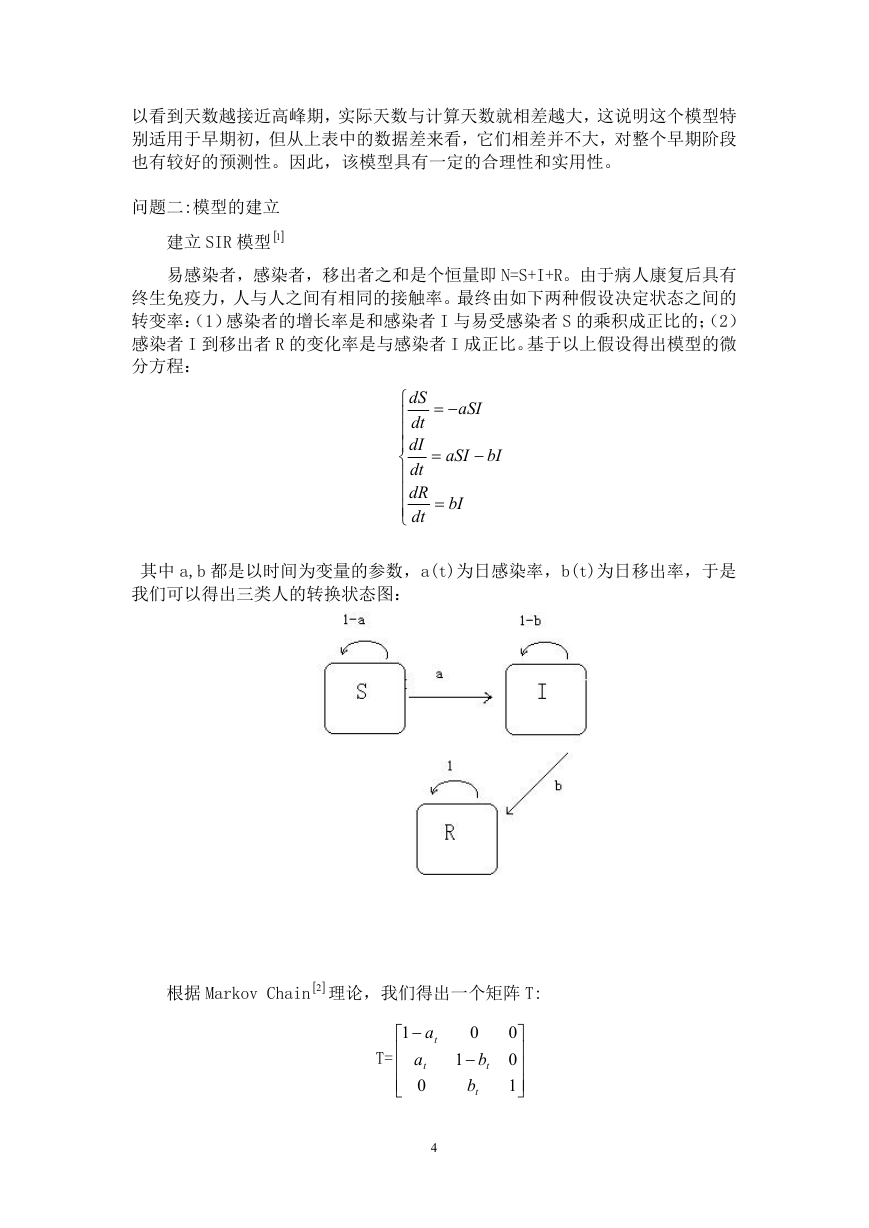
以看到天数越接近高峰期，实际天数与计算天数就相差越大，这说明这个模型特别适用于早期初，但从上表中的数据差来看，它们相差并不大，对整个早期阶段也有较好的预测性。因此，该模型具有一定的合理性和实用性。问题二:模型的建立建立 SIR 模型  1 易感染者，感染者，移出者之和是个恒量即 N=S+I+R。由于病人康复后具有终生免疫力，人与人之间有相同的接触率。最终由如下两种假设决定状态之间的转变率：（1）感染者的增长率是和感染者 I 与易受感染者 S 的乘积成正比的；（2）感染者 I 到移出者 R 的变化率是与感染者 I 成正比。基于以上假设得出模型的微分方程：          dS dt dI dt dR dt  aSI  aSI  bI  bI 其中 a,b 都是以时间为变量的参数，a(t)为日感染率，b(t)为日移出率，于是我们可以得出三类人的转换状态图：根据 Markov Chain  2 理论，我们得出一个矩阵 T: T= 1      t a  a t 0 1 0 b  t b t 0 0 1      4

其中 a t 就是当天易感染者 S 变为感染者 I 的日感染率,b t 就是当天感染者 I 转变为移出者 R 的移出率.( a t , b t 分别为 a(t)，b(t)某一天的值) 设初始值 X 1 ={N,0,0},于是我们可以由 X 与 T 的转置矩阵相乘,相乘一次得到第一天的易感染者,确诊病人及排除者的人数,再由该人数与 T 的转置矩阵相乘一次得到第二天各类人群的数目,依此类推,我们可以得到第 t 天的各类人群的数目,于是我们可以得出任何一天各类人群的数目的初步模型即: X 1t =X t *T ' 由于 T 是由 a,b 确定的,所以要建立模型还必须求出 a(t),b(t). 于是我们参照附件 2 中的数据，利用 Matlab 的多项式数据拟合，可以得到它们相应的多项式。下面进一步讲拟合过程：第一步：对附件 2 中的疑似病例进行 20 次数据拟合，得出每天的疑似病例数的多项式： f S (t)=238.2523-80.1594t+480.6525t 2 -325.9497t 3 +110.1561t 4 -22.3320t 5 + 2.9772t 6 -0.275t 7 +0.0181t 8 -0.0009t 9 …………………………（1）第二步：对附件 2 中已确疹的病例数据进行运算，新确诊的病例数 m(t)就是把当天已确诊病例数的累积 n(t)减去前一天确诊病例数的累积 n(t-1)即： m(t)=n(t)-n(t-1) 对 m(t)进行 20 次数据拟合，得出关于新增病例与时间的多项式： f I (t)=407.5716-569.7285t+476.2872t 2 -227.1678t 3 +67.6374t 4 -13.3813t 5 +1.8488t 6 -0.10854t 7 +0.0139 t 8 -0.0008 t 9 …………………（2）由第二步对 f I (t)求导得出 f I ' (t)，f I ' (t)表示为每天已确诊病例的变化情况，因为 f )(tS 是当天疑似病例数，所以得出 a(t)=f I ' (t)/f )(tS 。第三步：我们把死亡病例和治愈者都归为同一组 R 类，于是把他们相加得到每天的 R 类人群 K（t）,再由第二步的计算方法我们得到每天死亡和治愈的人数 l(t)即 l(t)=K（t）-K（t-1）然后对 l(t)进行二次数据拟合，得出关于每天死亡和治愈人数与时间的多项式： f R (t)=-0.0323t 2 +2.95235t-13.1284………………………(3) 第四步：按照第二步的方法对第二步中的 m(t)再进行一次二次拟合，得到 f I (t)的一个二次多项式： f I (t)=0.0561t 2 -5.7216t+141.7628…………………(4) 5

同理，由（3），（4）式可得 b(t)= f R ' (t)/f I (t) 即： )( ta  )( tb         f f f f I S R I ' ' ' )( t )( t )( t )( t (前面（1），（2），（3）,(4)式的 Matlab 拟合图及程序见附录 I) 通过上面的分析我们可以得到一个完整的模型: (I)  1t X )( ta         )( tb     ' I t ' * TX )( f t )( f t )( f t R )( f t S ' I 四模型的改进由于我们逐步对 SARS 的研究和认识,那么在不久的将来预防它的疫苗也将出现.显然医疗卫生部门就会对群众进行疫苗接种,于是我们的模型能够通过接种疫苗而进行改进,但是没有必要增加其他人群种类,我们可以简单而直接的把接种疫苗的人群从 S 中分离到 R 中,所以我们假定一个系数 c,它表示每天有 c 的人成功接种疫苗.(例,c=8%,表示每天有 8%的人成功接种疫苗),我们前面的 T 矩阵可以改为: T=  c  1      a t a t c 1 0 b  t b t 0 0 1      上面的模型就可以改进为:(II)  1 ' （其中 c 为常数） I t ' * TX )( t f )( t f )( t f R . )( t f S ' I   t X )( ta       )( tb    c  五模型的求解与结果分析 6

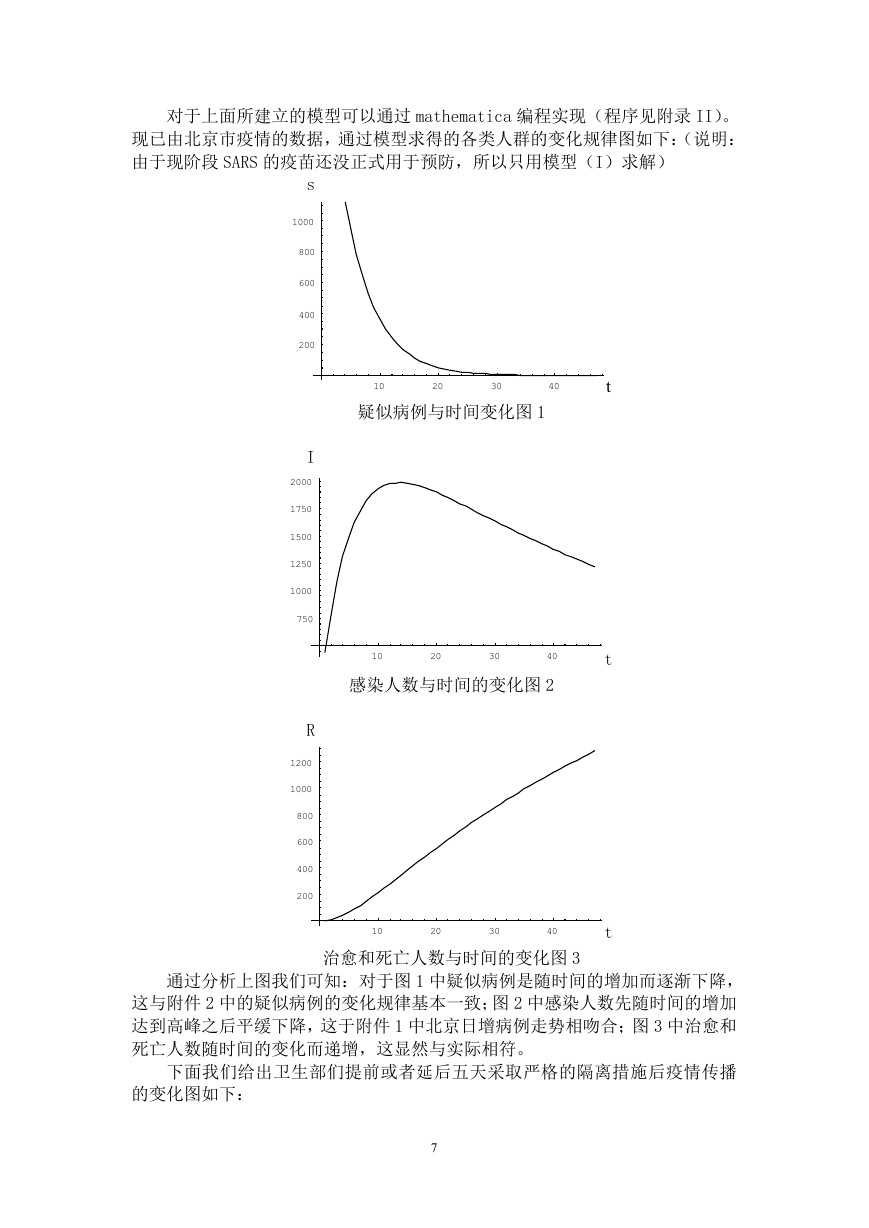
对于上面所建立的模型可以通过 mathematica 编程实现（程序见附录 II）。现已由北京市疫情的数据，通过模型求得的各类人群的变化规律图如下：（说明：由于现阶段 SARS 的疫苗还没正式用于预防，所以只用模型（I）求解） s 1000 800 600 400 200 I 2000 1750 1500 1250 1000 750 R 1200 1000 800 600 400 200 10 20 30 40 疑似病例与时间变化图 1 t 10 20 30 40 t 感染人数与时间的变化图 2 10 20 30 40 t 治愈和死亡人数与时间的变化图 3 通过分析上图我们可知：对于图 1 中疑似病例是随时间的增加而逐渐下降，这与附件 2 中的疑似病例的变化规律基本一致；图 2 中感染人数先随时间的增加达到高峰之后平缓下降，这于附件 1 中北京日增病例走势相吻合；图 3 中治愈和死亡人数随时间的变化而递增，这显然与实际相符。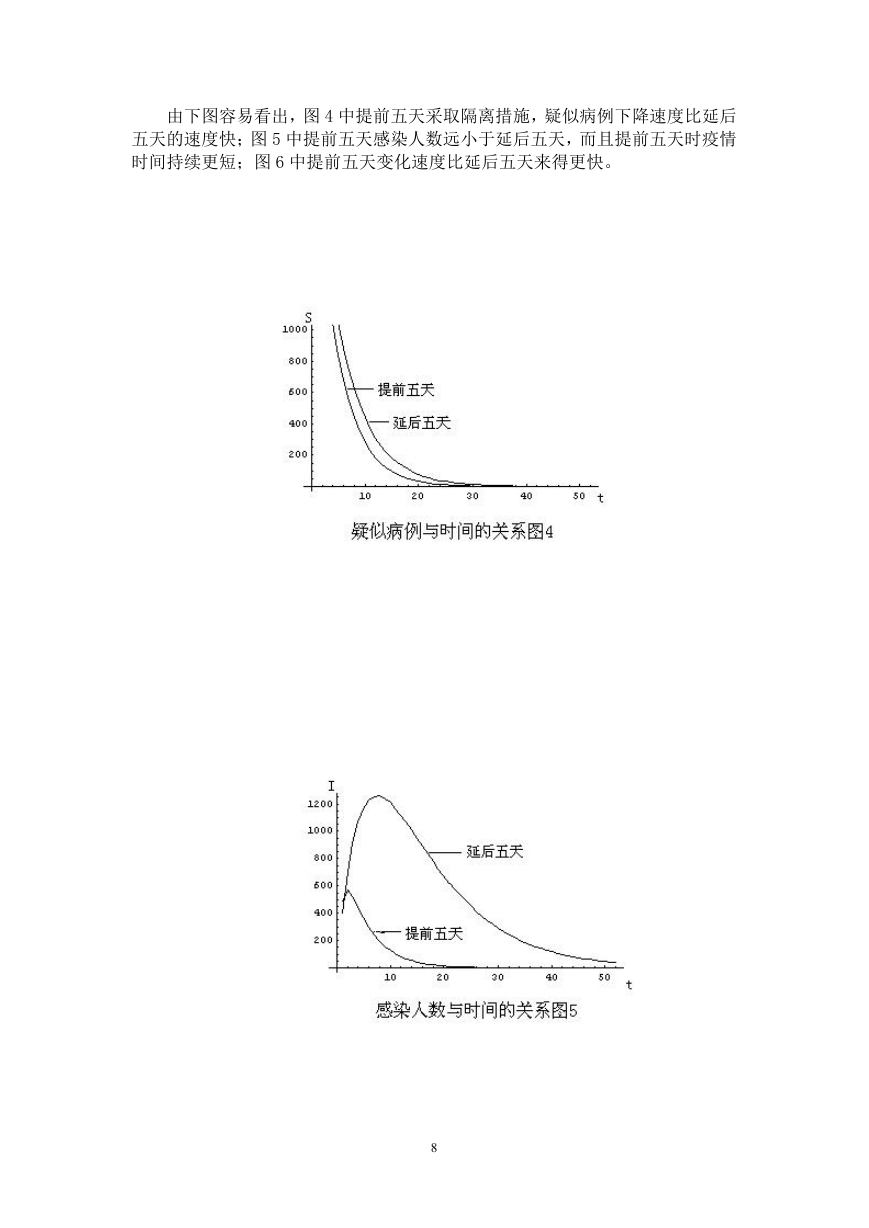下面我们给出卫生部们提前或者延后五天采取严格的隔离措施后疫情传播的变化图如下： 7

由下图容易看出，图 4 中提前五天采取隔离措施，疑似病例下降速度比延后五天的速度快；图 5 中提前五天感染人数远小于延后五天，而且提前五天时疫情时间持续更短；图 6 中提前五天变化速度比延后五天来得更快。 8

资料库

2003年全国大学生数学建模优秀论文.doc

相关推荐

行业

热门标签

最新资料