%BP 神经网络用于系统辨识训练预测程序 clear all clc %产生随机序列作为系统输入 A=6; x0=1; M=255; f=2; N=60;Q=2*N/3;H=N-Q-1; %初始化 for k=1:N x2=A*x0; x1=mod (x2,M); v1=x1/256; if v1-0.5>=0 %分别用 x2 和 x0 表示 xi 和 xi-1 %x2 除以 M 的余数给 x1 %x1 除以 256 得到小于 1 的随机数给 v1 u(:,k)=v1*f-1;%如果随机数 v1 大于 0.5，就乘以系数 f 减去 1，将结 else u(:,k)=v1-1; end x0=x1;%xi-1=xi v0=v1;%vi-1=vi end z=zeros(1,N); v=rand(1,N); for k=3:N %果存于 U 的第 k 列中 %不满足条件的运算结果存于矩阵 U 中 %输出长度 %随机噪声 z(k)=1.5*z(k-1)-0.7*z(k-2)+1.1*u(k-1)+0.3*u(k-2)-v(k-1)+0.2*v(k-2); end for k=1:N-2 %理想输出作为观察值 hl(k,:)=[-z(k+1),-z(k),u(k+1),u(k),v(k+1),v(k)];%样本矩阵 HL 赋值 zl(k)=z(k+2); %给样本矩阵 ZL 赋值 end HL=(hl-min(min(hl)))/(max(max(hl))-min(min(hl))); %数据归一化 ZL=(zl-min(zl))/(max(zl)-min(zl)); %数据归一化 p=HL(1:Q,:); p1=HL(Q:N-2,:); b1=ones(Q,1);b2=ones(H,1); P=[p,b1]; P1=[p1,b2]; T=ZL(1,1:Q)'; T1=ZL(1,Q:N-2)'; inputNums=6; outputNums=1; hideNums=10; lc=0.03; max_epoch=3000; error_goal=0.00001; B1=randn(1,hideNums); B2=randn(1,outputNums); w1=randn(inputNums,hideNums); %训练样本输入 %测试样本输入 %初始化 %增广训练样本 %增广测试样本 %训练样本理想输出 %测试样本理想输出 %网络输入层节点数 %网络输出层节点数 %网络隐层节点数 %学习率 %最大循环次数 %期望误差最小值 %输入层到隐含层的阈值初始化 %隐含层到输出层的阈值初始化 %输入层到隐含层的权值初始化 

w2=randn(hideNums,outputNums); W1=[w1;B1]; W2=[w2;B2]; error=zeros(1,max_epoch); %训练样本集 P 对 BP 神经网络进行训练 for k=1:max_epoch for i=1:Q for j=1:hideNums %隐含层到输出层的权值初始化 %输入层到隐含层的增广权矩阵 %隐含层到输出层的增广权矩阵 %训练误差 %单个样本的输入 net=P(i,:)*W1(:,j); y(i,j)=1/(1+exp(-net)); %隐含层神经元的输入 %隐含层输出 end Y(i,:)=[y(i,:),1]; for j=1:outputNums %带阈值隐含层输出 net=Y(i,:)*W2(:,j); O(i,j)=1/(1+exp(-net)); %输出层神经元的输入 %输出层输出 end E=T(i)-O(i); SSE=0.5*E^2; if SSE>=error_goal for c=1:hideNums for j=1:outputNums %单个样本训练误差 %均方误差 DW2(c,j)=(T(i,j)-O(i,j))*O(i,j)*(1-O(i,j)); %输出层误差偏导 W2(c,j)=W2(c,j)+lc*DW2(c,j)*Y(i,c); sumDW1=0; sumDW1=sumDW1+W2(c,j)*DW2(c,j); %输出层权值阈值的调整 %输出层对前一层的误差 end end for m=1:inputNums for n=1:hideNums DW1(m,n)=Y(i,n)*(1-Y(i,n))*sumDW1; W1(m,n)=W1(m,n)+lc*DW1(m,n)*P(i,m); %隐含层误差偏导 %隐含层权值阈值的调整 end end end end e=T-O; error(:,k)=sumsqr(e)/(2*Q); end w1=W1(1:inputNums,:) B1=W1(end,:) w2=W2(1:hideNums,:) B2=W2(end,:) %测试样本集 P1 用于 BP 神经网络预测 for i=1:H %样本集训练误差 %输入层到隐含层的权值 %输入层到隐含层的阈值 %隐含层到输出层的权值 %隐含层到输出层的阈值 

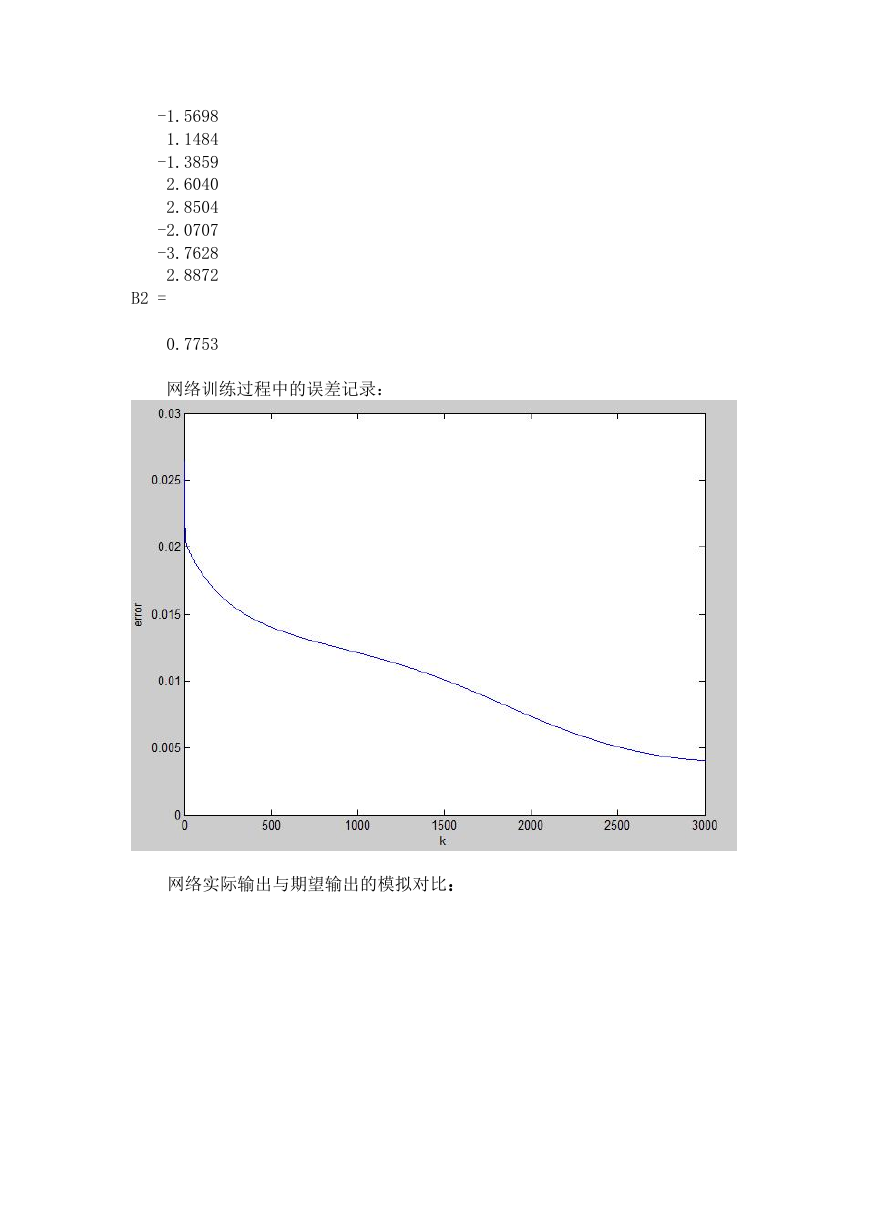
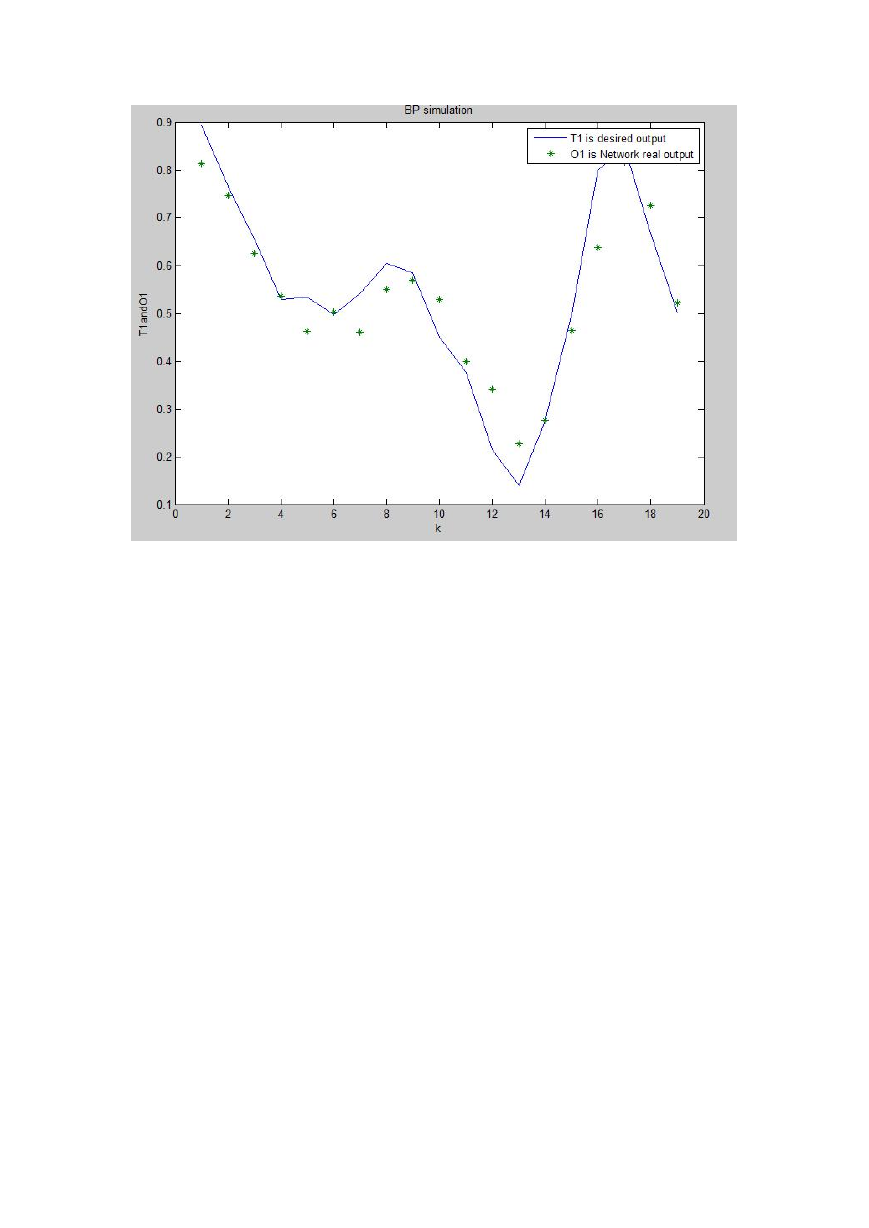
for j=1:hideNums net=P1(i,:)*W1(:,j); y(i,j)=1/(1+exp(-net)); %隐含层的输入 %隐含层神经元输出 end Y(i,:)=[y(i,:),1]; for j=1:outputNums net=Y(i,:)*W2(:,j); O1(i,j)=1/(1+exp(-net)); %BP 网络实际输出 %输出层的输入 end end figure(1); k=1:max_epoch; plot(k,error); xlabel('k');ylabel('error'); figure(2); k=1:H; plot(k,T1,k,O1,'*'); xlabel('k');ylabel('T1andO1');title('BP simulation'); legend('T1 is desired output ','O1 is Network real output'); %每次训练产生的均方误差 %期望输出值和 BP 网络实际输出值 程序运行结果： 网络调整后的权值和阈值： w1 = -1.8970 -1.4659 0.2206 2.3745 0.3982 0.6983 -0.0396 0.7766 -2.0508 -0.8974 0.5775 -2.0787 -0.3536 -0.8267 0.3110 1.0050 1.2206 0.7763 -0.0303 0.2509 -0.2577 -0.7947 0.2247 -0.0308 -0.7324 1.3088 -0.4352 1.9195 -0.3522 1.0435 0.1196 0.3865 -1.1566 -2.8680 -1.8290 1.4659 -0.2796 -2.9194 1.9239 1.6357 0.3303 1.6692 2.5735 -0.1207 -0.4017 -2.8010 1.2246 0.6319 -0.8915 -2.5360 0.2798 2.2846 0.1851 0.4378 1.9985 0.5372 -0.2822 -0.7683 -1.2297 0.4094 B1 = -0.0626 -0.7535 1.3940 -0.7373 -0.6442 -1.0483 -2.4781 0.6430 0.4005 -0.4490 w2 = 0.4787 -0.6121 

-1.5698 1.1484 -1.3859 2.6040 2.8504 -2.0707 -3.7628 2.8872 B2 = 0.7753 网络训练过程中的误差记录： 网络实际输出与期望输出的模拟对比：